井下超聲流量計的誤差分析

林龍貴

（貴州航天控制技術有限公司，貴陽550009）

1 引言

在貴州航天控制技術有限公司的井下超聲流量計開發(fā)成功之前，油田使用的流量計主要由浮子式、渦輪式、電磁式等幾種原理制造的產(chǎn)品，由于受井內(nèi)原油、泥沙和液體黏度的影響，這些流量計的測試精度和可靠性都較差。井下超聲流量計從原理上解決了粘度法測定聚合物流量的測試問題。

2 隨機誤差分析

隨機誤差是產(chǎn)品在相同條件下，多次重復測量同一物理量時，誤差值呈無規(guī)律變化的一種誤差，隨機誤差不能用實驗方法消除，也不能修正，只能依靠統(tǒng)計規(guī)律了解其分布特性[1]。

2.1 流量微分方程

流量公式：

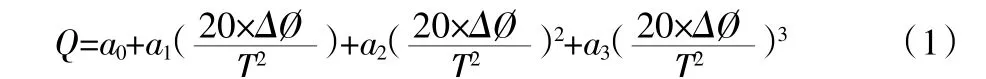
得全微分方程：

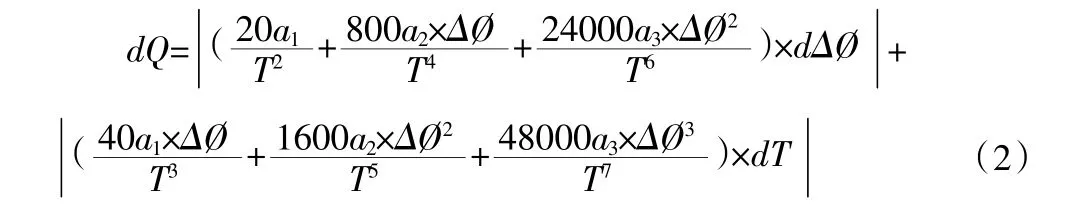
式中：

a0、a1、a2、a3——流量標定系數(shù)，（無量綱）；

T——超聲波傳播0.2m 所用的時間，（μs）；

Δ?——超聲波在順流、逆流中傳播0.2m 產(chǎn)生的相位差。

在式（2）中，由于dΔ? 和dT 的變化是隨機的（統(tǒng)計符合正態(tài)分布），所以兩部分的誤差取絕對值之和。

2.2 隨機誤差計算

對測試的數(shù)據(jù)進行統(tǒng)計后，得出了在同一條件下的流量測試的原始數(shù)據(jù)，其傳播時間“T”隨機變化dT=1～2μs，相位“Δ?”隨機變化dΔ?=10～20 個A/D 采集位，由于“T”和“Δ?”的隨機變化，導致了在同一條件下的流量Q 的隨機變化。

在以下的誤差計算中，設T=134μs（多數(shù)儀器測試的時間“T”為130μs-140μs=134μs），dT=1μs，dΔ?=10（針對多數(shù)儀器的dT、dΔ? 的變化范圍），帶入式（2）得：

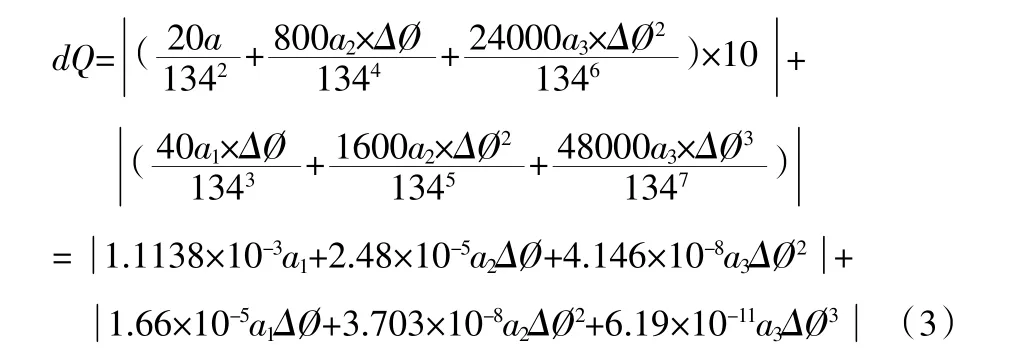
式（3）即為隨機誤差估算公式。

3“相位法”誤差分析

3.1 原理誤差分析

在實際測試中，如果水溫較高、壓力較大，則聲速“c”變大、時間“T”變小；又根據(jù)“可知，“”，此式說明流量Q 的自變量“不受聲速“c”的影響；但在相位法測試中，儀器只測試其相位“Δ?”隨聲速“c”的變化（原理上“Δ?”與“c2”成反比，“T2”成正比），忽略其時間“T”隨聲速“c”的變化，從而使“”與聲速“c”成反比，進而使Q 流量與聲速“c2”成反比，這是相位法測試中產(chǎn)生的原理誤差，即在高溫、高壓環(huán)境中實測的流量Q 會比真實流量小（即Q實測≤Q真值）。

3.2 原理誤差估算

在誤差估算中，取時間T2=1000（這是相位法計算中給定的值），聲速c 從1480～1555m/s，即水溫從20～70℃時聲速的變化（沒有考慮壓力對聲速c 的影響）。則：

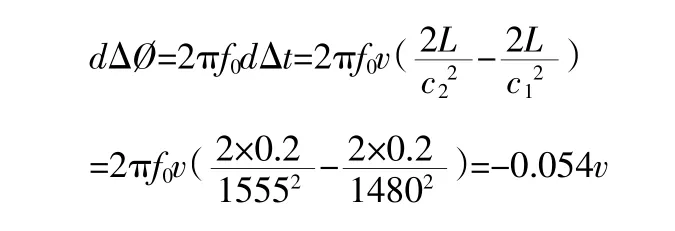
將dΔ? 變成A/D 采集值：

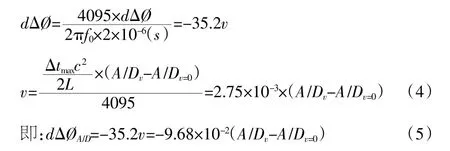
式（4）（5）中：

dΔ?A/D——dΔ? 的A/D 采集值；

A/Dv=0——流速為“0”時的A/D 采集值；

A/Dv——流速為“v”時的A/D 采集值；當v=0 時，A/Dv=A/Dv=0。

在式（8）中，Δt 取2μs（即2μs 所產(chǎn)生的相位的A/Dv采集值為4095），c 取1500m/s，式（5）中的“-”號表示當聲速“c”變大時，相位的A/D 采集值變小，即實測流量變小。

又根據(jù)相位法求流量的公式：

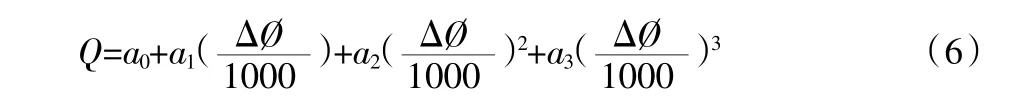
得相位法誤差公式：

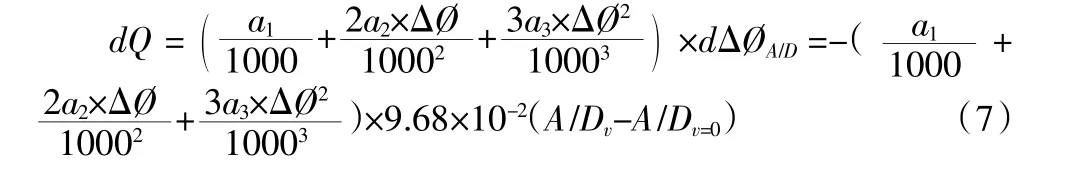
4“相位-時間法”誤差分析

根據(jù)式（1），考慮到Δ? 和“T”的綜合影響，求全微分方程為：

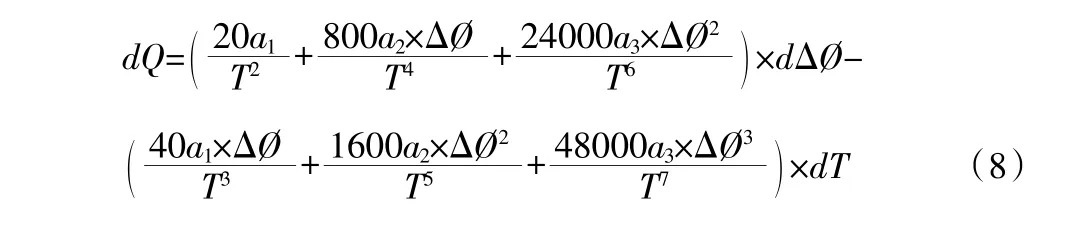
此式與式（2）的區(qū)別在于沒有絕對值符號，這給兩部分誤差的相互抵消帶來了可能。

當聲速“c”從1480m/s 變到1555m/s 時，dΔ?A/D(max)的表達式和式（5）一樣，即：dΔ?A/D=-35.2v=-9.68×10-2（A/Dv-A/Dv=0）；

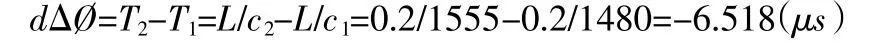
在式（8）中，取T=134μs，結合上兩式得：

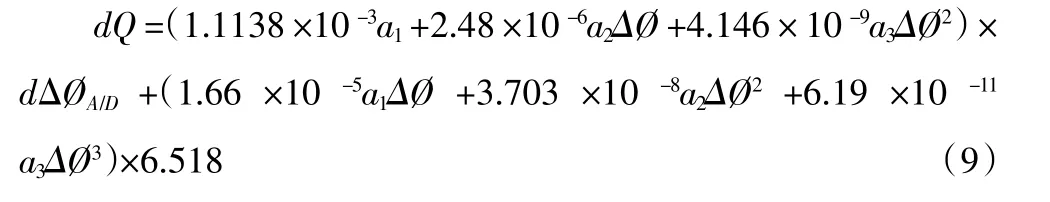
式（9）即為“相位-時間法”在聲速“c”從1480m/s 變到1555m/s 時的誤差估算公式。

5 誤差的驗證

5.1 隨機誤差估算的驗證

統(tǒng)計出04A057 號儀器的相位Δ?max=800，帶入式（3）得：

對04A057 號儀器的標定（標定精度為1.74%）得：

a1=126.58903，a2=8.71896，a3=-5.56843 代入式（10）得：dQ100=0.166+1.71=1.876(m3/d)，即隨機相對誤差=1.88%。

在隨機誤差估算中，流量誤差的產(chǎn)生由兩部分組成：即由“dΔ?”產(chǎn)生的相位測試誤差和由“dT”產(chǎn)生的時間測試誤差之和。從A-100m3/d、A-200m3/d、A-300m3/d 的標定數(shù)據(jù)看：相位測試誤差的絕對值比較小（均在1m3/d 以下）、而時間測試誤差的絕對值隨量程的增大而增大，相對誤差之和隨量程的增大而減小，但最大不大于3%（F·S）。

根據(jù)誤差分配原則+，在溫度、壓力變化不大的情況下，采用相位法（x 法）克服了“dT”的影響，即排除了時間測試誤差，所以更容易標檢合格。

以上隨機誤差的大小依賴于儀器的測試精度和換能器的穩(wěn)定度。

根據(jù)誤差理論，該隨機誤差遵循正態(tài)分布，并且可針對具體的流量臺階的多次測試數(shù)據(jù)計算出特定流量條件下的標準偏差“σ”及精密度指數(shù)“h”。由于隨機誤差的概率密度分布函數(shù)計算需要依靠大量的統(tǒng)計數(shù)據(jù)才能保證其準確性，統(tǒng)計和計算的工作量大，故忽略此環(huán)節(jié)。

5.2 相位法誤差估算的驗證

以下驗證中的方程形式為：Q=a3x3+a2x2+a1x+a0，其中x=Δ?/1000，Δ? 為相位的“A/D”采集值（即Δ?=A/Dv）。

對03A052 號儀器進行相位標定得實際擬合方程：

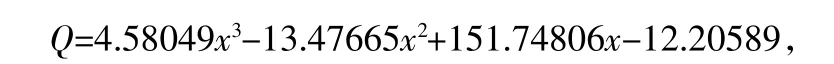
取A/Dv=794(實測最大值)，A/Dv=0=80(實測零位)，則由式（5）得：dΔ?A/D(max)=-9.68×10-2×714=69.12，將dΔ?A/D(max)代入式（7）得：

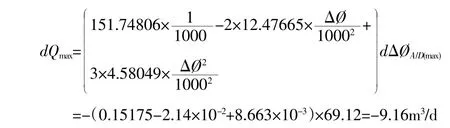
即聲速在1480～1555m/s 時產(chǎn)生的相對誤差為：

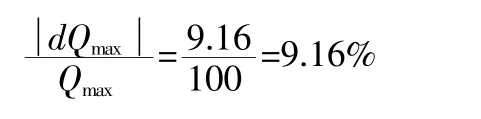
從上看出，當聲速“c”從1480m/s 變到1555m/s（即水溫從20℃變到70℃）時，相同的實際流量，測試時可差10%左右，反映到實際生產(chǎn)過程中，超差的儀器大部分出現(xiàn)在水溫變化較大的時候。

6 結論

依據(jù)對流量計存在的隨機誤差、“相位法”誤差和“相位-時間法”誤差的分析結果，結合流量計目前的技術水平，可以認為：

①隨機誤差是暫時無法消除的（誤差一般在2%～4%左右），它主要由換能器決定，這也是造成流量標定精度較高、而檢定精度較低；或流量標定精度較低、而檢定精度較高的主要原因；

②“相位法”誤差屬于原理性誤差。當工作環(huán)境變化較大時會產(chǎn)生較大的誤差，如果考慮壓力的影響，則誤差將會更大；

③“相位-時間法”誤差也屬于原理性誤差。主要由電路產(chǎn)生的相位零位引起，因為相位零位是流速=0m/s 時的相位，由此看見，從原理上就把相位分成了兩部分：固定相位，和流速相位，相位本來隨聲速“”變化，樣這一來，為常數(shù)的“固定相位”和“流速相位”一起變成了自變量。目前，生產(chǎn)的流量計的設計零相位均在70～150 個A/D 值左右，所以由于零相位帶來的誤差均在2m3/d 左右。

消除“相位-時間法”誤差的辦法是在擬合方程時減去零相位，這一點在以后的計算中可以進一步完善。

綜上所述，可以得出兩條結論：

第一，在今后的流量標檢中，只能采用“相位-時間法”；第二，隨機誤差遵循正態(tài)分布，且主要受測試時間“”的影響，所以，在儀器標檢超差（超差幅度為：4%以內(nèi)）的情況下，可以將上下?lián)Q能器對換后重新標檢，但超差大于4%時要另找其他的原因。