非互易旋電材料硅基矩形波導的色散特性研究*

王慧瑩 王智2)? 崔粲 李航天 李強 詹翔空 王健 吳重慶

1)(北京交通大學理學院光信息科學與技術研究所,發光與光信息技術教育部重點實驗室,北京 100044)

2)(集成光電子學國家重點聯合實驗室,北京 100083)

1 引 言

光子單向邊緣態是2008年由普林斯頓大學的Haldane(2016年諾貝爾物理獎得主)提出的[1],他預言了磁光光子晶體的邊界可以存在單向電磁邊界模式(one-way electromagnetic edge mode,OWEM)[1?3],即被約束在磁光光子晶體邊界的表面波,其主要特征是它的群速度僅指向一個方向.由于外磁場的作用,磁光晶體介電張量中的非對角元發生改變,產生旋電各向異性,時間反演對稱性被破壞,使得被局域在介質與等離子材料交界面的表面等離子體(surfaceplasmons,SPs)表現出非互易傳播的特性[4,5],這種非互易SPs被稱為表面磁等離子激元(surface magnetoplasmons,SMPs)[6,7].當等離子材料的電子回旋頻率與其等離子頻率的量級大小可以比較時,SMPs的漸近頻率在前后兩個方向上會有明顯不同,使得SMPs在兩個不同漸近頻率間隔之間的區域單向傳播,而完全不存在反向傳播模式,反向的散射被完全抑制.2009年,麻省理工大學的Wang等[3]首先在微波系統中使用磁光材料光子晶體,用實驗證明了OWEM的存在.此后,不斷有科研工作者對單向光子晶體波導進行研究,實現了光隔離器[8?12]、光環形器[13?16]、光開關[17,18]等非互易光學器件.近期的研究主要集中在磁光材料混合的太赫茲平面波導結構[19,20].例如2017年,Tsakmakidis等[20]設計的波包進出時間非對稱的磁光材料混合平面波導系統,其中的平面波導支持光子單向邊緣態,因此系統的洛侖茲互易性被打破,在太赫茲波段將傳統的時間-帶寬限制提高了兩個數量級.

本文對光通信C波段旋電材料的非互易矩形波導進行討論,研究在外磁場作用下表面磁等離子體激元在旋電材料矩形波導中非互易傳播的特性.利用有效折射率法[21]推導矩形波導中導模的色散方程,通過數值計算分析矩形波導結構及材料參數的改變對其非互易色散關系、時延特性的影響.

2 非互易矩形波導結構及色散方程

2.1 波導結構與旋電材料介電張量

光通信C波段旋電材料的矩形波導結構的截面如圖1所示,該波導由電介質層(Si)、光通信C波段旋電半導體層(gyroelectric semiconductor,GS)以及四面有界的外包層(Ag)組成.其中波導芯區的y方向和Si層x方向的寬度分別為2a和d,選取Si和GS交界面的中心為原點建立二維直角坐標系,z軸垂直于紙面向里.在–y方向上對旋電半導體層施加靜磁場B0,由于磁場對介電張量的影響[2]使得SMPs在旋電材料矩形波導中沿z軸正方向非互易傳輸,打破了該波導系統的洛倫茲互易性[20].

外加磁場與光傳輸方向垂直并與波導分界面平行,根據法拉第效應,介質在電磁場作用下,介電常數為二階張量[6,19]表示為

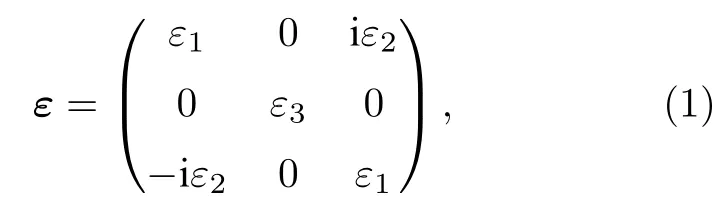
2.2 有效折射率法推導矩形波導色散方程

利用有效折射率法,把一個二維矩形波導近似看成兩個一維平面波導(planar waveguide,PW)的組合,即x方向受約束的平面波導PW1和y方向受約束的平面波導PW2,分別見圖2(a)和圖2(b).

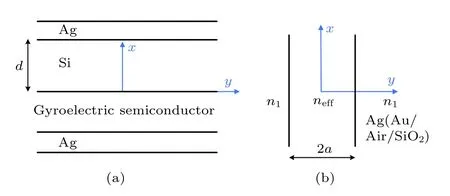
圖2 有效折射率法的兩個等效平面波導截面圖(a)x方向受約束的平面波導PW1;(b)y方向受約束的平面波導PW2Fig.2.Sectional views of two equivalent planar waveguides by effective refractive index method:(a)Planar waveguide PW1 with x direction constraint;(b)planar waveguide PW2 with y direction constraint.

波導外包層(xd)

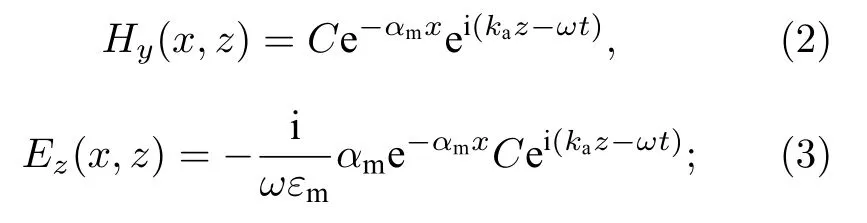
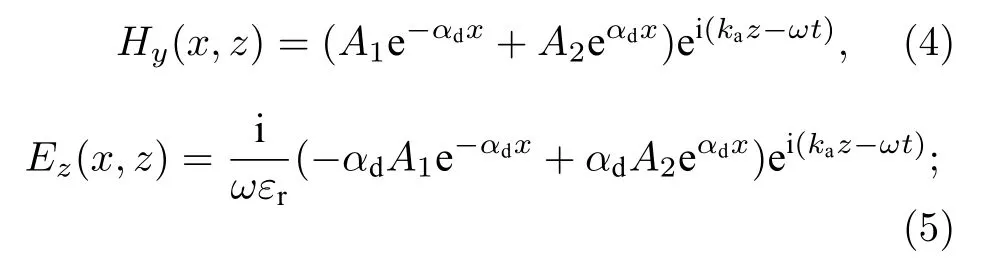
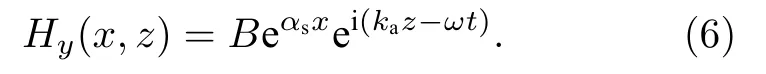
對電各向異性介質,在主軸坐標系中D=εE,利用(1)式可得

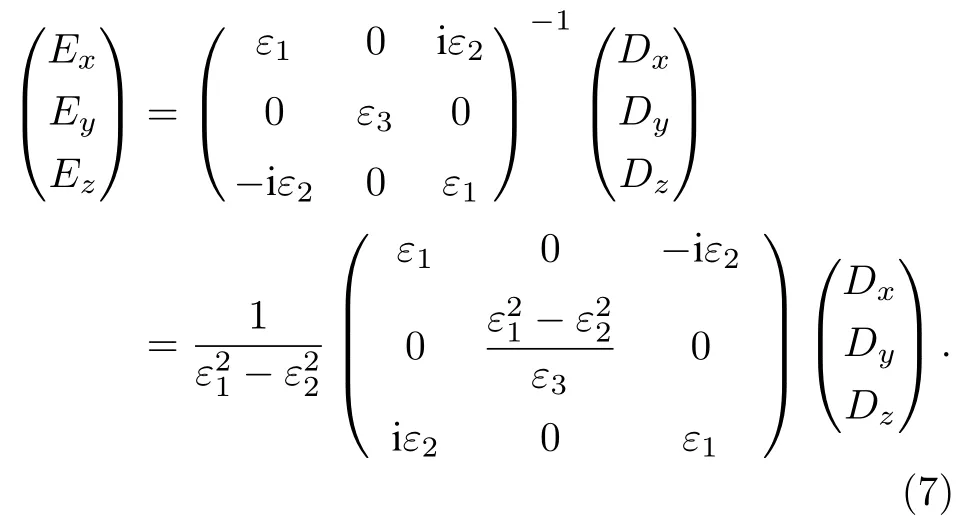
由(7)式得到電場分量Ez,

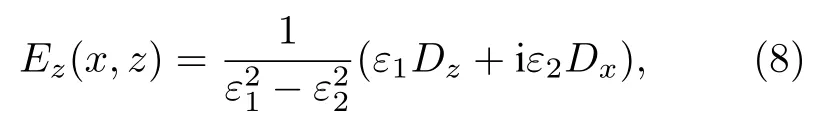
分別利用x=0 和x=d處的邊界條件,即Hy,Ez連續,可得到關于待定系數A1,A2,B,C的方程組:

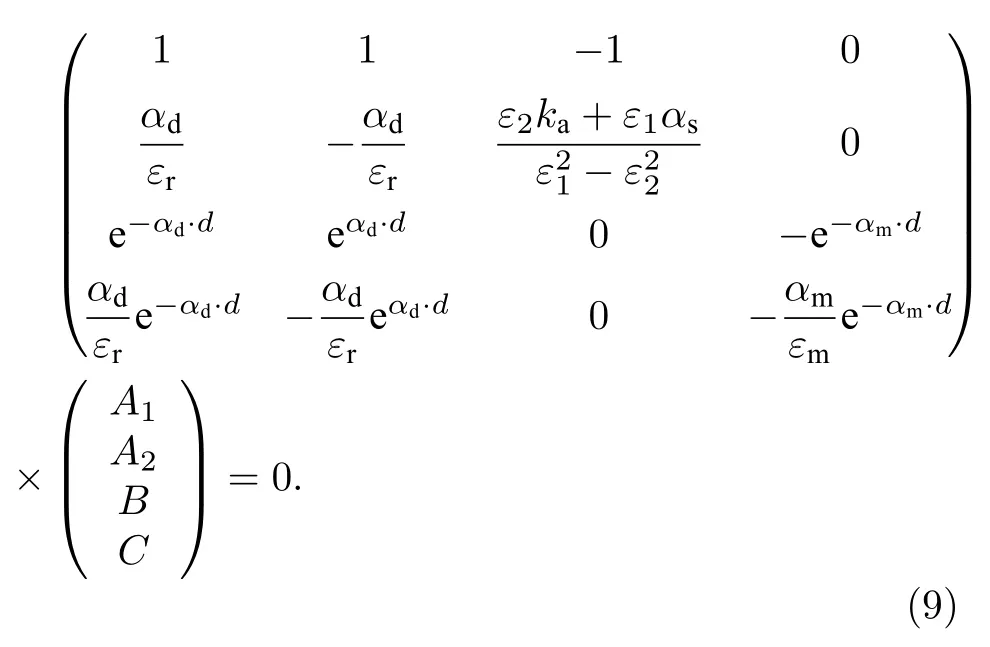
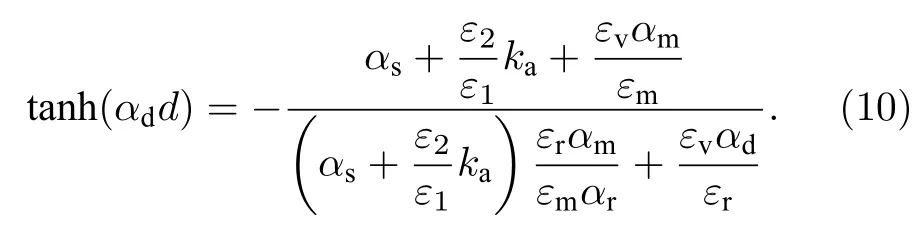
方程中參數及其含義如下:ka為的傳播常數;在電介質 Si層其中k0=ω/c為真空中傳輸波的波矢,Si的相對介電常數為該層厚度為d=0.14λp,其中λp=2πc/ωp,ωp=5.1613π×1014rad/s;在旋電半導體層αs=為旋電半導體 Voigt介電常數;在波導外包層外層材料的介電常數.

由(10)式可計算得到ka-w關系,從而得到有效折射率即y方向約束的平面波導PW2的芯區折射率.

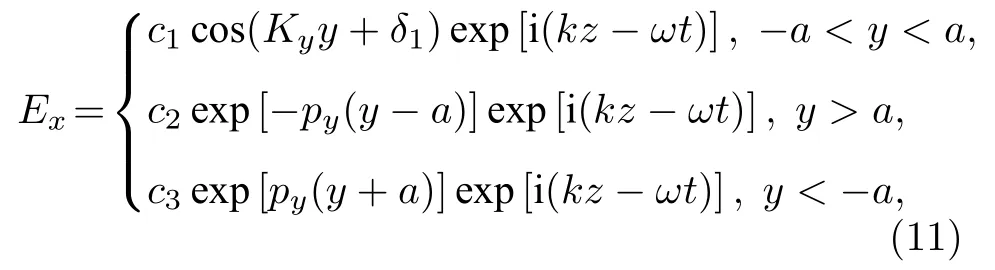
在PW2中y軸方向的y=±a處,即波導左右外包層與波導芯區的兩個交界面,利用Ex,連續的邊界條件,分別可以得到Ex和連續.

在y=a處,

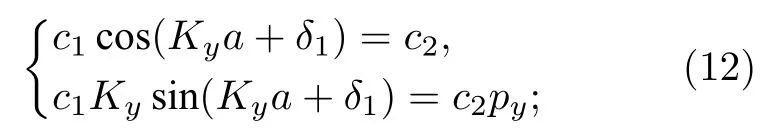
在y=–a處,

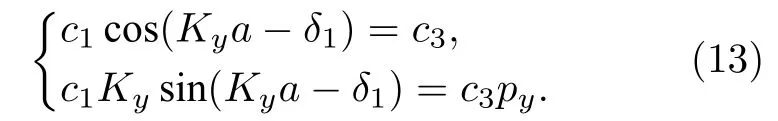
消去方程組(12),(13)中的待定系數,可以得到

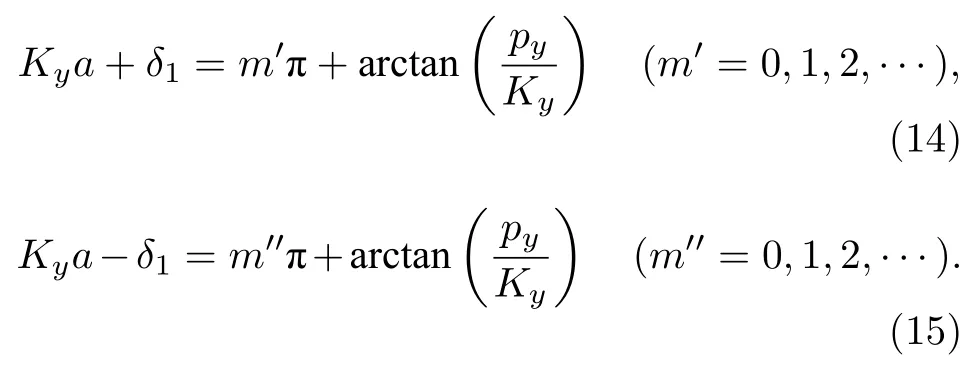
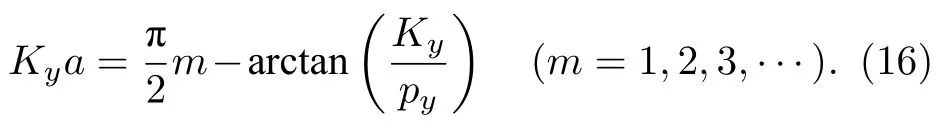
3 波導寬度對非互易色散特性的影響

利用色散方程(16)計算出不同芯區寬度的矩形波導色散曲線,如圖3(a)所示,波導結構為Ag材料四面包裹電介質層和旋電半導體層,參數見2.2節.由于對洛倫茲互易性的破壞,其色散曲線關于波矢k不對稱,在不對稱的頻率(圖中兩紅色水平虛線之間)區域內可以實現完全的單向傳輸,波導表現出非互易性.從圖3(a)可以看出,隨著矩形波導半寬度a由 0.02lp,0.04lp,0.06lp,0.08lp,0.12lp增大至 0.16lp,其色散曲線自然趨向平面波導的色散曲線(圖3(a)藍色實線),但是非互易的頻率區間基本不變.

為了討論非互易波導的緩存性能,圖3(b)給出了不同半寬度a的矩形波導,其SMPs波歸一化群速度vg/c=dω/(c·dk)與歸一化角頻率w/wp和歸一化傳播常數k/kp的關系.從圖3(b)可以看出,不管是隨著w(虛線)增大還是隨著k(實線)增大,均出現SMPs波群速度減慢現象.為了研究波導寬度對群速度減慢效應的影響,圖3(c)給出了工作波長l在1530,1550和1565 nm處的歸一化群速度隨波導寬度的變化.波導半寬度a在0.06lp(波導寬度 2a=140 nm)與 0.10lp(2a=233.5 nm)之間的vg相對較低,在約0.08lp處達最小值.而且隨l減小,vg減小,圖中最小群速度達到 5.43×10–2c.這一結論表明,寬度適當的矩形波導的非互易慢光效應比平面波導的非互易慢光效應更明顯,而且在C波段工藝容差較大(約為93.5 nm).

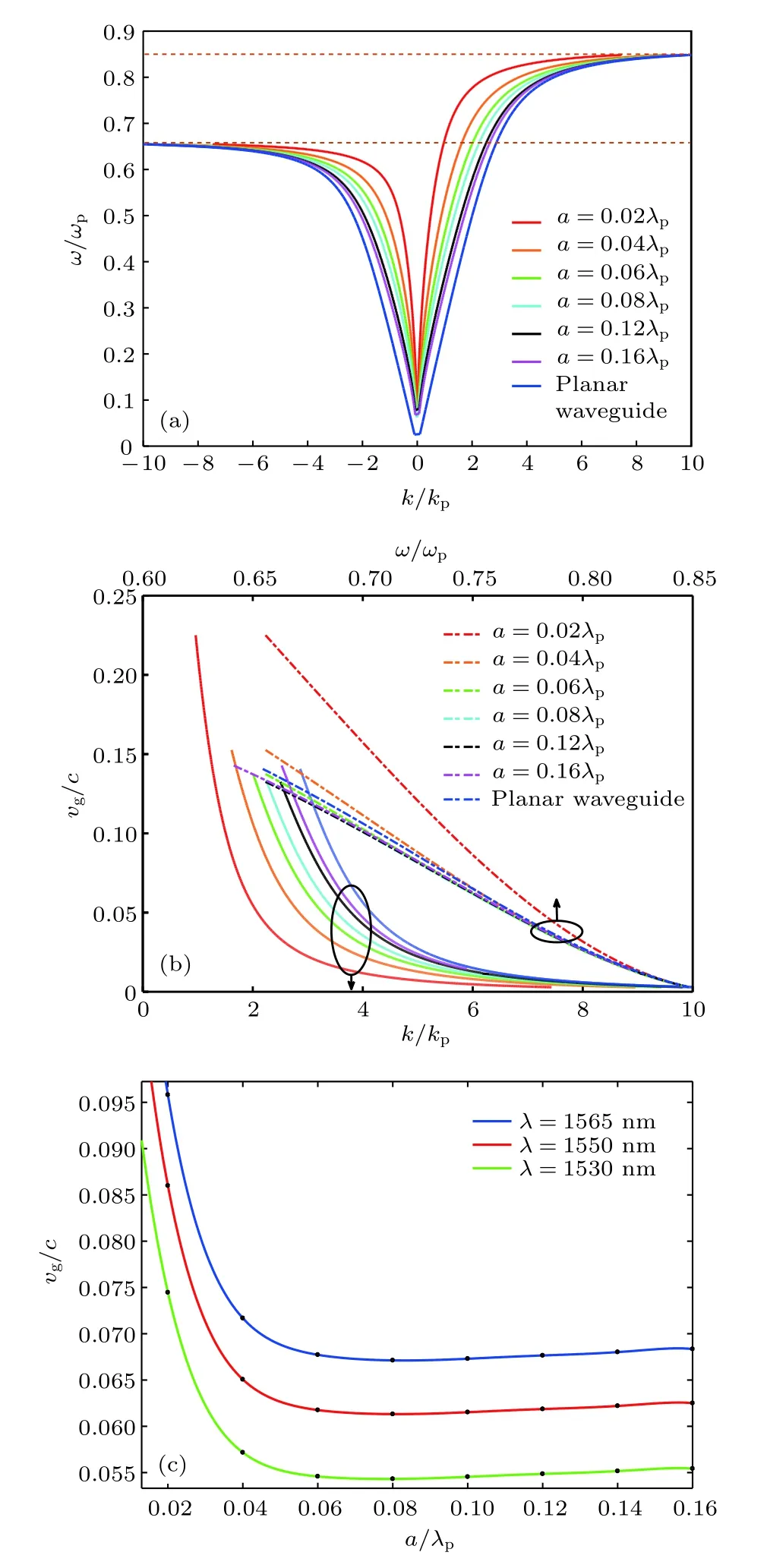
圖3 (a)不同芯區寬度的矩形波導色散曲線;(b)不同芯區寬度的矩形波導中SMPs波單向傳輸區域的群速度;(c)不同波長的SMPs波群速度隨芯區寬度的變化Fig.3.(a)Dispersion curves of rectangular waveguide with different core widths;(b)group velocity of one-way SMPs transmission region in rectangular waveguide with different widths;(c)variation of group velocity of SMPs with different wavelengths with different core widths.

4 折射率對非互易色散特性的影響

本文計算了矩形波導左右外包層分別為半導體 SiO2、空氣 Air、金 Au、銀 Ag 時的色散曲線,如圖4(a),材料折射率從 0.14,0.52,1.00 到 1.45,其色散曲線逐漸趨向平面波導色散曲線.圖4(b)是單向傳輸區域中SMPs波歸一化群速度vg/c與歸一化角頻率w/wp和歸一化傳播常數k/kp的關系,該圖顯示出與圖3(b)相似的規律,即SMPs波vg隨w(虛線)或k(實線)的增大而減慢.隨著材料折射率遞減,SMPs波群速度逐漸減小,群時延增大,慢光效應越明顯.矩形波導左右外包層材料為 Ag 時 SMPs波群速度最小(vg=2.8×10–3c),慢光效應最顯著.

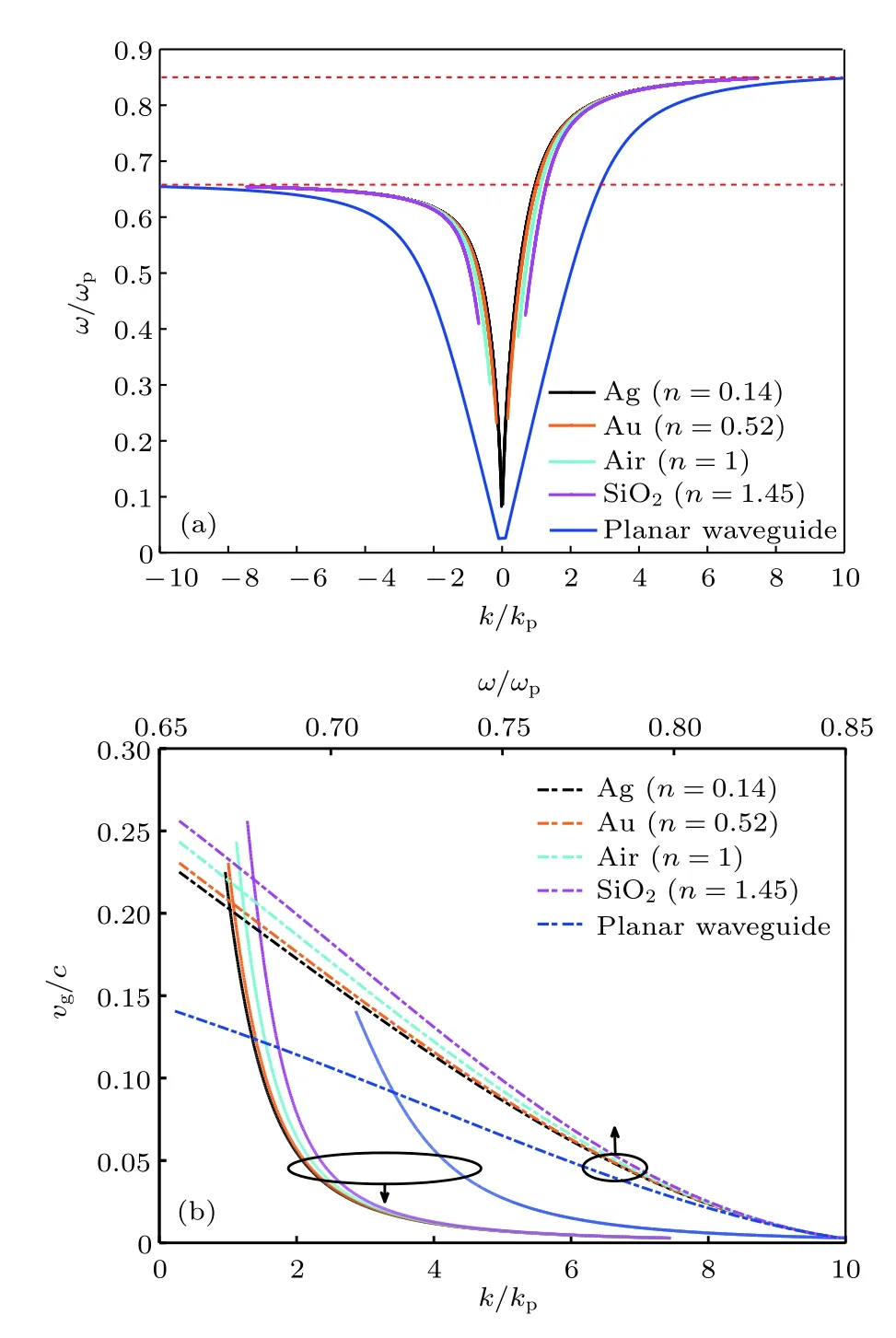
圖4 (a)不同材料的矩形波導色散曲線;(b)不同材料的矩形波導中SMPs波單向傳輸區域的群速度曲線Fig.4.(a)Dispersion curves of rectangular waveguide with different materials;(b)group velocity of one-way SMPs transmission region in rectangular waveguide with different materials.

5 結 論

本文理論分析了一種基于光通信C波段旋電材料的矩形波導結構,研究了該矩形波導在外磁場作用下表面磁等離子體激元非互易傳播的特性,推導了矩形波導中導模的色散方程,并對其色散關系、時延特性進行了分析.由于洛倫茲互易性的破壞,該矩形波導的能帶結構關于波矢k不對稱,在不對稱的頻率區域內可以實現完全的單向傳輸.矩形波導芯區寬度和外包層材料折射率對非互易色散特性有明顯影響,SMPs波群速度隨w,k減小,且矩形波導的慢光效應優于平面波導,在C波段可獲得約93.5 nm工藝容差.Ag包裹波導時,SMPs波的群速度最小可達 2.8×10–3c.