基于有效介質理論的物理性能計算模型的軟件實現*

孫楠楠 施展? 丁琪 許偉偉 沈洋 南策文

1)(廈門大學材料學院,廈門 361005)

2)(廈門大學航空航天學院,廈門 361102)

3)(清華大學材料學院,北京 100084)

1 引 言

近年來,隨著計算機技術的發展以及理論方法的完善,科研人員對一些材料的結構形成、結構與性能之間的定量關系進行了計算模擬[1?5].傳統的逐點實驗方法不僅耗費大量的人力物力,而且實驗周期漫長,其結果也存在偶然性.預先對實驗進行理論模擬計算不僅可以更好地指導實驗工作的開展,也可以對實驗結果進行驗證,還可以縮短實驗周期、節約人力物力[6,7].

復合材料具有從原子尺度到顯微結構尺度再到宏觀尺度的多尺度、多層次的結構特征.廣義上講所有的非均質材料都可以稱為復合材料,但是不同尺度上的處理方法不同.顯微結構尺度是指材料結構為納米級以上甚至達微米級的尺寸范圍,該尺度上主要研究材料顯微結構的形成與演變及表征、顯微結構與性能之間的定量關系以及進一步的材料顯微結構設計[2].狹義上講復合材料指的是顯微結構尺度下的多相復合材料,討論夾雜物、析出物、增強相與性能之間的定量關系.這類材料具有可調節性和可設計性,其性能也并非其組成材料性能的簡單加和平均[8].因此,可以通過改變組成材料的種類、組合方式來改變復合材料的有關性能,從而設計出具有某種優異性能的新材料.

對于確定材料結構與物理性能之間定量關系的理論方法已有諸多的研究,并且形成和發展了各自的理論體系,但每種理論都有其前提條件和適用范圍[2].主要的理論方法有:1)第一性原理[9,10]及均化方法[11,12]是通過先得到局部尺度(非均勻性尺度)水平上的精確解,然后利用幾何周期性得到宏觀尺度上的線性性能.該方法主要適應于周期結構.2)非均質材料的細觀力學[13]方法是以Eshelby[14]的等效夾雜原理為基礎,最先應用于解決復合材料線彈性問題,后來逐步推廣到解決非線彈性問題等方面.3)有效介質理論[15]是用于確定材料顯微結構與物理性能定量關系的理論方法,它假設第二相隨機分布于基體相當中.有效介質理論從有效介質近似[16]起,經歷了多階段的發展過程,現已成為一種較為成熟的理論方法.近年來,國內外學者將多重散射理論[17,18]應用于復合材料物理性能計算當中,如有效質量密度[19?22]、有效彈性模量[2,23,24]、有效介電常數[2,25,26]等,推動了有效介質理論的進展.改進的有效介質理論方法[2]將有效介質理論與細觀力學等其他方法結合,構造了一個系統地描述和預示復合材料顯微結構與性能定量關系的理論框架.在改進的有效介質理論中,通過較少的假設,盡可能多地考慮各項顯微結構因素(包括增強體長徑比、體積含量、取向分布角、宏觀取向角、界面性質與厚度),涵蓋力學、電學、磁學等物理場的單一場性能,以及多場之間的交叉耦合性能(如壓電、磁致伸縮、磁電耦合),它可以對常見的多種結構的復合材料進行計算.

目前復合材料物理性能計算理論較多,但這些理論大多模型復雜,計算步驟繁瑣,缺少操作方便的模擬計算軟件.本文基于改進的有效介質理論,針對復合材料彈性模量和介電常數兩項物理性能,推導了理論公式,并設計開發了Composite Studio物理性能計算軟件.該軟件除了實現基本的內核功能之外,采用了求解和分析獨立運行的工作方法.首先構建大數據量的計算組合進行求解,然后再設定不同的分析提取方式,分析顯示計算結果.該工作方式可以有效地提高計算效率,降低使用者的使用門檻,利于軟件的推廣使用.

2 基本原理

2.1 復合材料物理性能與平均場理論

材料的物理性能包含了熱、力、磁、電場下的物理性能.這些物理性能是材料前期設計時需要考慮的重要數據.

(1)式為材料物理性能的本構方程.其中,K為物理性能,J為響應場,F為內源場.性能K可以理解為單位源場F下產生的響應場J.單一場性能指的是源場F和響應場J都屬于同一類型的物理場,比如彈性模量、介電常數、磁導率.

通常,在平衡(穩態)、無內源場情況下,材料對外場的響應J是一個無散量,即

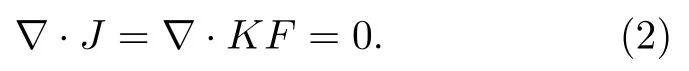
復合材料的有效性能是復合材料的整體表現,通常用平均場的方式來定義,即平均場產生的平均響應的大小,如(3)式所示:

從(3)式可以看出,復合材料的有效性能求解,主要是平均場和平均響應的求解.在一些理想結構中,場的分布容易求解.對于一般的顯微結構,精確地求解場分布,是一個復雜的物理問題.

采用格林函數[2,15]可以有效地對多種顯微結構進行平均場、平均響應的求解,核心問題是采用格林函數求解平衡方程,即(2)式.對于非均勻介質,可以看作是在一個均勻介質的微區中引入異質顆粒,在這個局部位置上,均勻介質的均勻性遭到破壞,根據微擾觀點,局部的K(x)可以表示為

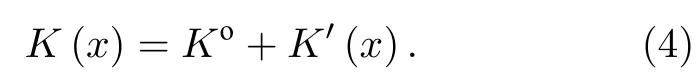
(4)式中,Ko為均勻介質的相應性能參數,它不依賴于空間位置;K'(x)是一個微擾項,它包含了K(x)中的所有隨機變化.進一步得到非齊次平衡方程

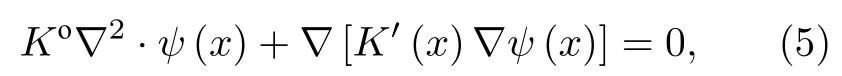
其中,?2表示拉普拉斯算子,y是對應場F的勢函數.該方程的解可直接由對應的格林函數求出

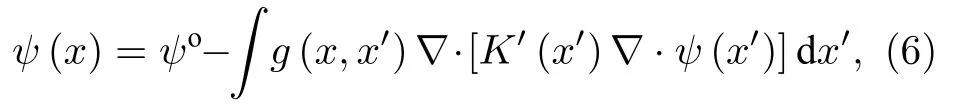
其中,ψo不依賴于變量K′,它是該均勻介質中的均勻勢,通過分部積分可以得到局部場的解為

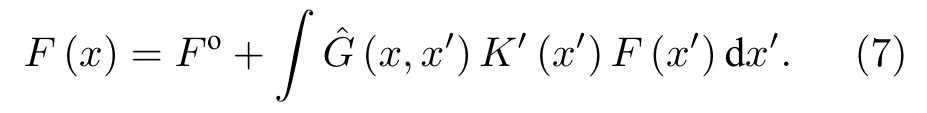
引入一個多重散射“t矩陣”張量

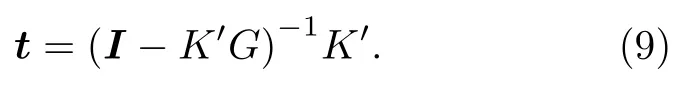
其中I為單位陣,進一步可把局部場寫成

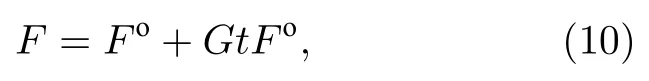
通過對局部場變量取平均,可最終得到復合材料的有效性能

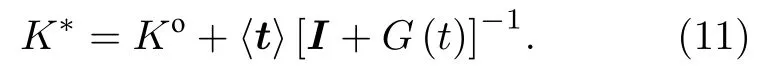
(11)式是對復合材料的有效性質的普適解,但是實際上復合材料的顆粒夾雜多數是多顆粒問題,難以得到格林函數和t矩陣的精確解,因此,根據參考均勻介質的不同,通常采取兩種近似來計算有效性質.當忽略顆粒間的相互作用時,可將Ko近似為基體相應的物理性能,該種近似適合于低濃度的顆粒彌散結構,對于各向同性球形顆粒的輸運問題,(11)式可變為 Maxwell-Garnett[2,15,27]方程.若考慮顆粒的相互作用,可將Ko近似為復合材料的有效性能K*,稱為耦合勢近似,或自洽近似,此時參考介質的性質即為復合材料的性質本身,顆粒嵌入參考介質引起的微擾影響最小,對于各向同性球形顆粒的輸運問題,(11)式可變為Bruggeman[2,15,28]方程.因此,Maxwell-Garnett方程與 Bruggeman方程均為有效介質理論普適解的兩個特例.

2.2 復合材料幾何模型與顯微結構因素

復合材料主要由基體、增強體和界面組成,其真實顯微結構十分復雜,為了簡化,假設基體為無窮大的連續介質,而增強體用簡單的旋轉橢球體來模擬[2].在這種幾何模型的假設下,顯微結構因素包括增強體的體積分數、長徑比、截止取向分布角、宏觀取向角.復合材料整體基于增強體隨機分布的假設,采用統計平均的方式求解等效性能,適用于大部分常規意義上的復合材料.當涉及到某些性能取決于精密的周期性結構,如光子晶體的特征散射行為,本模型并不適用.

在體積分數和長徑比方面,增強體用旋轉橢球體等效后,旋轉橢球體的體積分數和長徑比是結構的兩個重要因素,這也是復合材料調整性能的兩個重要手段.

在截止取向分布角方面,增強體在基體中通常是無規分布的,如圖1所示.為了描述這種分布的混亂情況,引入纖維的取向分布角的概念,即每根纖維的局部坐標系的軸和宏觀坐標系X3軸的夾角.而截止取向分布角θcutoff,就是所有纖維的取向分布角的最大值,這個值可以衡量取向分布的混亂程度.在計算中,假設纖維取向在截止分布角構成的分布錐內均勻分布.在這樣的定義下,θcutoff為 180°表示完全無規分布,θcutoff為 0°表示完全有序,纖維全部平行排列.在實際材料中,影響取向分布的通常是工藝,例如復合材料的注塑過程的流體流動經常使增強體產生顯著的擇優取向.

圖1 qcutoff規分布纖維的截止取向分布角Fig.1.Cut-off orientation distribution angle of randomly distributed fibers.

在宏觀取向角方面,當復合材料呈現各向異性后,彈性模量和介電常數隨測量方向的變化也是一個需要關注的問題.宏觀取向可以由3個歐拉角來嚴格描述,由于復合材料通常具有∞ mm的對稱性[2],為了簡化軟件操作,本文的計算中宏觀取向角只考慮了影響最大的章動角,即兩個坐標系x3坐標軸的夾角.其中x3軸為∞ mm的旋轉對稱軸.

3 軟件設計與界面

3.1 軟件設計

Composite Studio物理性能計算軟件由C++語言/Qt編程完成.采用C++語言編寫了計算內核,采用Qt設計了友好的人機界面.C++語言可以方便日后的升級和功能擴展,以及引入其他計算模塊.Qt是一種圖形化程序設計框架,方便獲得可視化界面.

計算內核包含了格林函數、角度取向平均、彈性模量計算、介電常數計算、T矩陣計算以及基本的數學函數集.功能界面主要包含材料參數庫、材料種類選擇、功能參數選擇和計算結果做圖分析等.

3.2 軟件界面

3.2.1 軟件主界面—材料庫

圖2為材料參數庫界面,在此界面可以添加或者刪除材料,也可以對材料參數進行編輯.對于各向異性材料,勾選“anisotropic”可以輸入介電常數張量、彈性常數張量的各個分量.這些材料可以作為后續計算中的基體、增強體等.

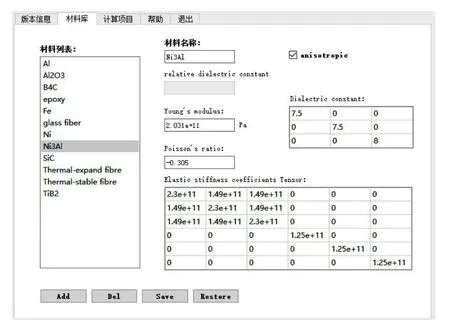
圖2 材料庫輸入界面Fig.2.Input interface of the material library.

3.2.2 軟件計算流程

圖3為Composite Studio物理性能計算軟件計算流程圖,首先設定復合材料的顯微結構因素,然后設定計算模型的類型,并求解計算,最后對結果做圖分析.這些步驟都由軟件的可視化界面完成,由人機交互完成計算模型信息的輸入.軟件預設了顆粒復合、短切纖維復合、長纖維復合三種復合材料類型.其中顆粒復合和長纖維復合分別對應了長徑比為1、長徑比為無窮大的特例.選擇基體與增強體性質的步驟如圖4(a)所示,即從材料庫中直接導入基體材料和增強體材料的性質參數.圖4(b)為關鍵的復合材料結構參數設置界面,包括了體積分數、長徑比、截止分布角、宏觀取向角四個結構參數.設定參數范圍和間距,可以構建相應數量的組合.例如,體積分數設定10個點、長徑比設定10個點、截止分布角10個點、宏觀取向角10 個點,則構建的計算組合數為 10×10×10×10=104個.通過減小間距,可以構建數目非常大的計算組合數.這些組合進入求解內核,選擇物理性質以及自洽/非自洽方式進行復合材料有效性質的計算.其中,自洽模型認為(4)式中的參考介質就是復合材料的性能本身(Ko=K?),通過迭代求解.而非自洽模型通常以固定的參考介質進行求解,忽略顆粒間的相互作用.這兩種模型是常用的復合材料近似方式.計算得到所有組合的有效性質后,對計算結果進行作圖分析,得到有效性質隨各個顯微結構因素的變化關系曲線.

圖3 計算流程圖Fig.3.Flow chart of the calculation.

圖4 顯微結構參數輸入界面Fig.4.Input interface of microstructure parameters.

3.2.3 計算結果分析

目前Composite Studio軟件開發了復合材料有效彈性模量與有效介電常數的計算模塊.圖4的參數設置界面構建了一個數量很大的參數組合集合,如果把每個可變參數當作一個維度,計算結果實際上是一個多維數組.為便于分析,軟件設計了對每一個參數的單獨分析模式,從結果的多維數組中提取出二維的性質-參數變化曲線.

圖5和圖6分別為玻璃纖維/環氧樹脂復合材料的有效彈性模量,以及CaCu3Ti4O12/聚氨酯復合材料的有效介電常數的計算結果.可以看出,計算結果包含了4個結構參數(包括體積分數、長徑比、截止分布角、宏觀取向角)下的性質-參數變化曲線,可以滿足分析需要.為了便于使用,設計了參數聯動同步變化的功能,即如果改變4個顯微結構參數中的某一個參數,其他3個圖形相應的結構參數也會進行同步地改變,省去了對參數的反復設置.最后,軟件還設計了單點分析功能,可以對任意一個組合的性質進行提取.如圖6所示,在“單點分析”區域,當選定確定的結構參數后,其物理性能計算結果直接呈現在下面的物理性能矩陣列表中,可供研究者直接獲得計算結果.

圖5 Composite Studio 物理性能計算軟件計算結果—彈性模量Fig.5.Calculation results of physical performance calculation software Composite Studio—elastic modulus.

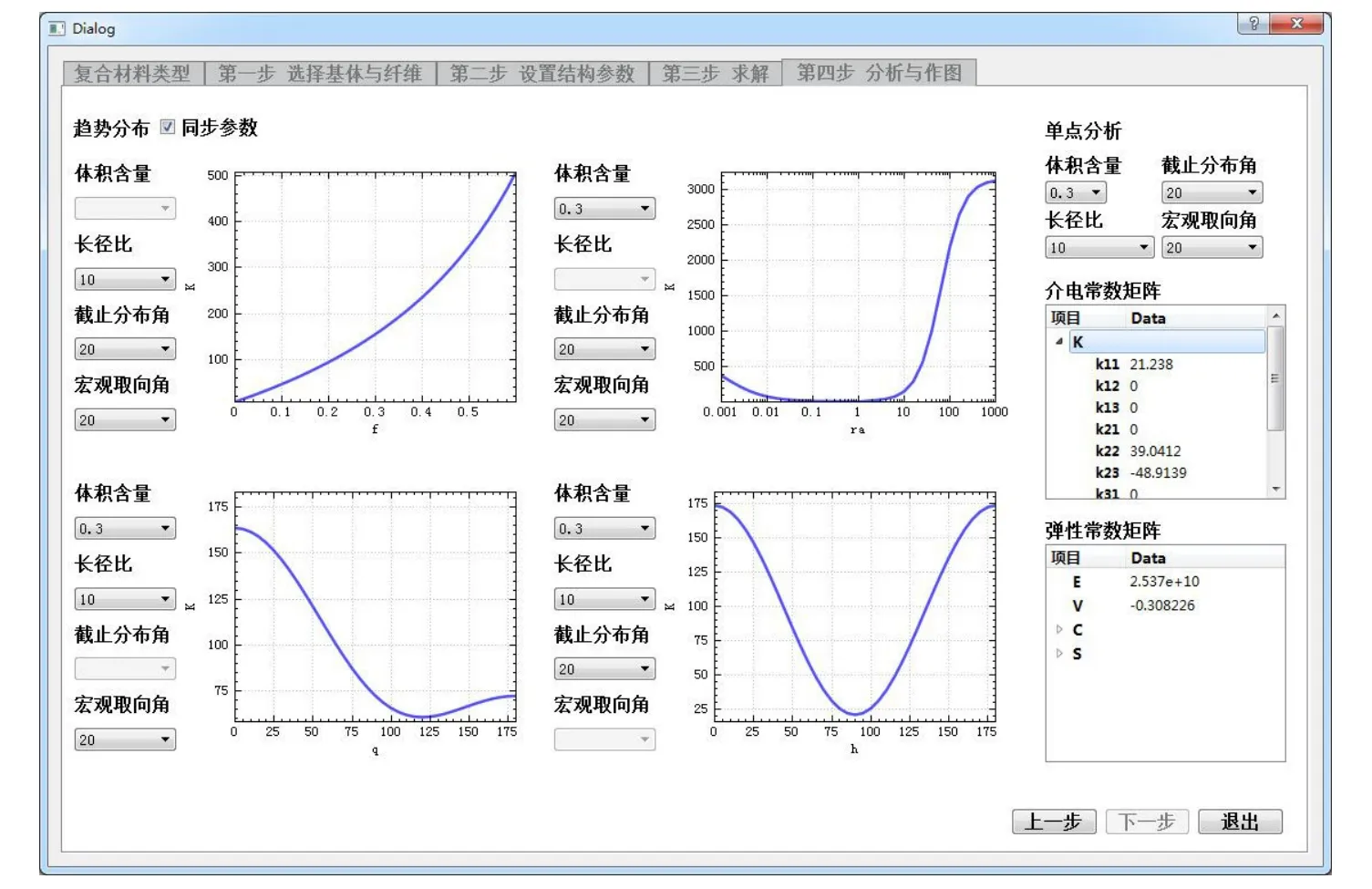
圖6 Composite Studio 物理性能計算軟件計算結果—介電常數Fig.6.Calculation results of physical performance calculation software Composite Studio—dielectric constant.

4 結 論

本文基于改進的有效介質理論,采用C++/Qt混合編程,開發出了一款可跨平臺應用的復合材料物理性能模擬計算軟件—Composite Studio,包含彈性模量和介電常數兩個計算模塊.軟件采用了計算和分析獨立工作的運行方式,創建顯微結構參數疊加組合的104量級以上的結構組合數進行高通量計算,后續分析篩選不再重新計算,提高了計算效率,降低了使用者的門檻.Composite Studio物理性能計算軟件可以作為一種通用的計算工具,未來將嵌入大型服務器平臺,開放用于復合材料的材料設計.