火箭整流罩聲振環境縮比特性研究

榮吉利，范博超，程修妍，諶相宇

(1. 北京理工大學宇航學院，北京 100081；2. 中國工程物理研究院電子工程研究所，綿陽 621900)

0 引 言

運載火箭在飛行過程中主要受到氣動噪聲[1]和噴流噪聲的影響，由燃氣射流引發的氣動噪聲可達到160 dB以上[2]。外部噪聲以寬頻、隨機的形式通過透射和輻射傳遞到整流罩內部[3]，直接影響到有效載荷的可靠性，甚至導致整個任務失敗，發生災難性的事故[4-5]。因此整流罩聲振環境的研究是不可或缺的一項重要內容。

目前，對整流罩聲振環境的研究主要采用數值仿真和試驗測量兩種方法。工程中采用的數值仿真方法主要有：有限元方法(Finite element method,FEM)、邊界元方法(Boundary element method,BEM)和統計能量分析方法(Statistical energy analysis,SEA)。韓峰等[6]采用FEM/BEM方法，對航天飛行器中的圓錐殼結構進行了聲振耦合仿真計算，并與試驗進行了對比，仿真曲線的最大峰值與試驗測量相差在2 dB之內。杜驪剛[7]采用NASTRAN對某飛行器在噪聲環境下的振動響應進行了預示并與噪聲試驗作了對比，主要測點總均方根誤差在6 dB以內，驗證了使用三維有限元模型進行振動環境預示方法的有效性。韓增堯等[8]對衛星太陽翼在噪聲環境下的加速度響應進行了詳細研究，利用SEA法對太陽翼的聲振力學環境進行了預示，并通過與試驗結果對比，驗證了上述方法的可行性。Pirk等[9]采用了SEA方法研究運載火箭聲振模型，并由此開展了噪聲控制研究。采用混合FEM-SEA法，朱衛紅等[10]建立了航天器聲振預示模型，預示了航天器全頻段聲振環境，通過試驗對比驗證了預示方法和模型的有效性。

由于全尺寸試驗成本高、難度大且不易于快速測量試驗數據，縮比模型試驗作為取代全尺寸試驗的一種重要手段得到廣泛應用。陳勁松等[11]提出了模擬火箭發射初期燃氣噴流縮比試驗的5個基本相似參數：線性幾何尺寸比、燃燒室壓強、環境壓強、燃氣比熱比、燃氣火藥力，在滿足這5個相似參數的情況下，縮比模型試驗的燃氣流場結構與原型試驗的燃氣流場結構保持線性幾何相似關系。Doug等[12-13]在預示Ares I火箭起飛噪聲環境、點火超壓環境時應用縮比模型噪聲試驗方法得到了較好的結果。Morgan等[14]將火箭發動機縮比模型進行了簡化，用簡化后的縮比模型試驗獲得了發動機近場噪聲，但其誤差較大。任方等[15]基于相似理論，根據幾何相似、噴流參數相似、發射環境相似來預示起飛噪聲環境，得到了運載火箭表面噪聲環境的空間相關特性。以上方法均未通過理論分析和仿真校驗的角度為飛行狀態下整流罩縮比試驗進行指導。

本文基于量綱分析進行了火箭飛行過程中整流罩聲振環境的縮比特性研究，推導并獲得了不同縮比模型與全尺寸模型之間內部聲場、壁面振動加速度的關系，使用有限元方法進行了仿真計算，校驗了縮比準則的正確性。因此，在聲振環境試驗中可參考本文的縮比準則設計縮比模型試驗。

1 理論分析

1.1 有限元聲振耦合理論

聲學有限元方法可以同時考慮內外聲場并建立結構與內外聲場耦合的模型。具體而言，首先對結構建立有限元結構離散方程，對聲場建立有限元聲學系統方程，然后考慮聲振耦合面的相互作用，并在結構有限元動力學方程中加入聲場對結構的作用項，在聲學系統方程中加入結構對聲場的作用項，聯立方程就可以建立起結構與內外聲場耦合的動力學方程[16]：

(1)

式中：Ks，Cs和Ms分別為結構有限元的剛度矩陣、阻尼矩陣和質量矩陣;ρ0為聲學介質密度;ω為角速度;Kc為聲學介質與結構耦合剛度矩陣;Ka,Ca和Ma分別為聲學有限元的剛度矩陣、阻尼矩陣和質量矩陣;u與p分別為結構位移向量與聲壓向量；Fs與Fa分別為外載荷與聲載荷激勵向量。

1.2 量綱分析

噪聲是隨機聲環境，以聲譜、聲壓級、空間相關等參數描述。遠場聲功率與聲壓的關系式為：

(2)

式中：W為聲功率；R為聲波傳播的半徑；ρ0c0為介質的特性抗阻。

因此，決定整流罩內部聲壓強度特征的控制參數來自以下3個方面：

1)聲源參數：聲功率W，振動頻率f，聲源到整流罩內部的距離R。

2)介質參數：密度ρ0，聲音在介質中的傳播速度c0。

3) 結構參數：密度ρs，彈性模量Es，泊松比νs，厚度hs，阻尼比ζ。

于是，整流罩內部聲壓p是上述控制參數的函數：

p=F(W,R,f;ρ0,c0;ρs,Es,νs,hs,ζ)

(3)

取ρ0，c0和W作為基本量，式(3)可轉化為下面的無量綱關系：

(4)

如果縮比模型與原模型聲學介質參數相同，且結構材料相同，則6個有關參數與原模型保持相同，即

(ρ0,c0;ρs,Es,νs,ζ)=const

(5)

則式(4)可簡化為

(6)

根據相似律，若要使整流罩縮比模型內聲場psca與原模型p相等，則要滿足：

(7)

由式(5)可知，式(7)簡化后為：

(8)

式中:下角標sca表示縮比模型參數。

通過上述分析可知，假設聲源聲功率W的縮比比例為Wsca/W=α2，振動頻率變為fsca=(1/α)f，聲源到整流罩內部的距離Rsca=αR，結構厚度變為hs,sca=αhs，則縮比模型與原模型的內聲場相同。

同理，整流罩壁面振動加速度是式(3)中控制參數的函數，簡化后的無量綱式為

(9)

根據相似律：

(10)

即當聲功率W的縮比比例為α2時，縮比模型整流罩的壁面振動加速度asca=(1/α)a。

2 仿真校驗

2.1 仿真模型

參考某火箭整流罩的結構，使用Virtual.lab軟件建立了如圖1所示的整流罩有限元模型。壁面結構模型為蒙皮，為三角形殼單元。聲學模型包括外部包絡網格和內部聲腔網格，均為四面體聲學網格，外部包絡網格的外表面定義為自適應匹配(AML)層，原模型的結構網格量為8536，聲學網格量為308401。

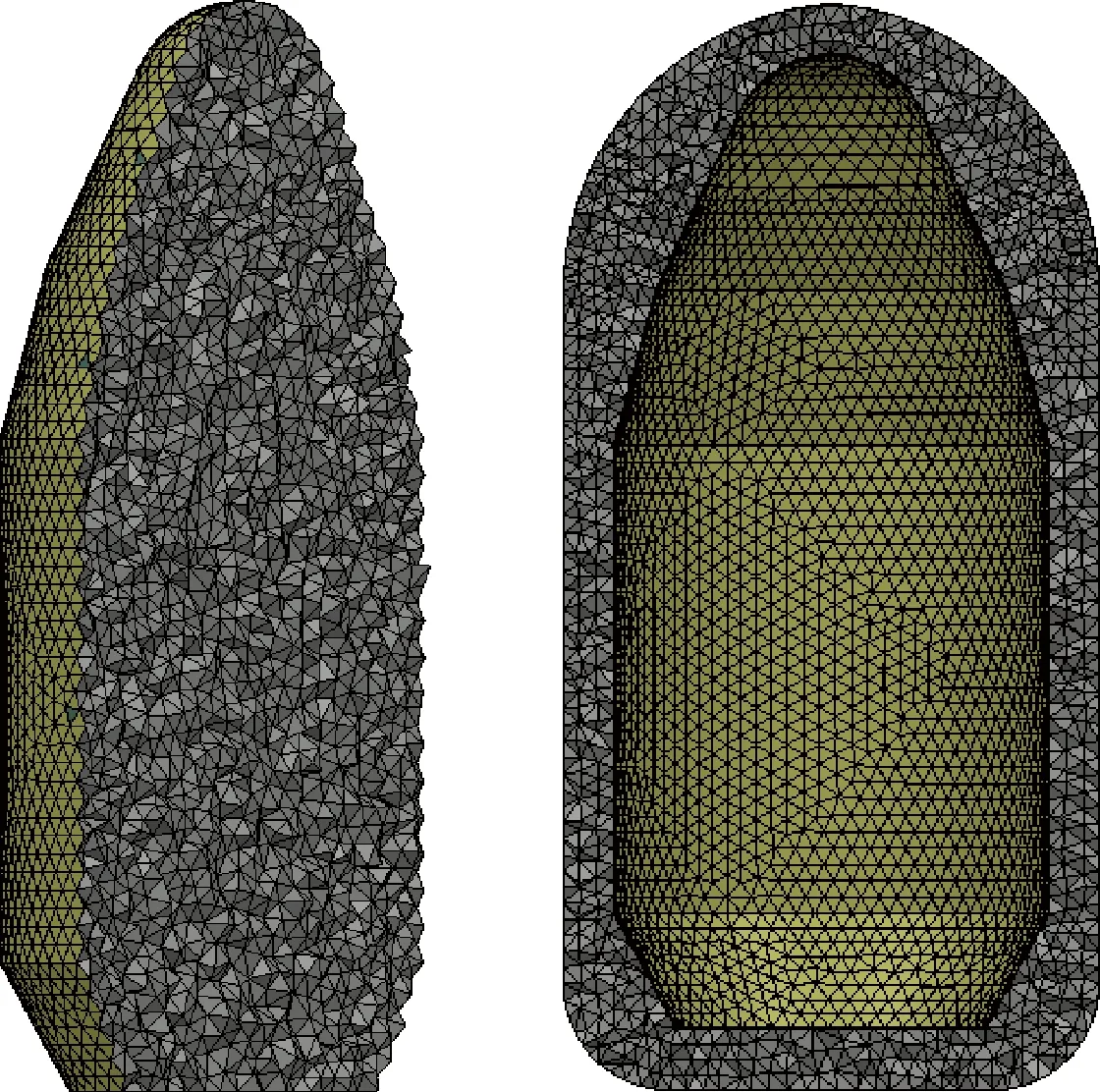
圖1 整流罩有限元模型Fig.1 The finite element model of the fairing

在整流罩地面噪聲試驗中，通常將整流罩放置于混響室，采用揚聲器作為聲源激勵來產生高聲壓級的外噪聲環境，并采用麥克風獲取整流罩內外的聲壓數據。參照混響試驗條件，在聲學仿真中采用24個分布式平面波模擬試驗條件下的混響環境，這24個平面波均布在以整流罩為中心的球面上，如圖2所示。將整流罩與空氣接觸位置的結構網格和聲網格定義聲振耦合關系，采用基于結構模態的聲振耦合算法計算內聲腔的響應和整流罩的壁面振動。

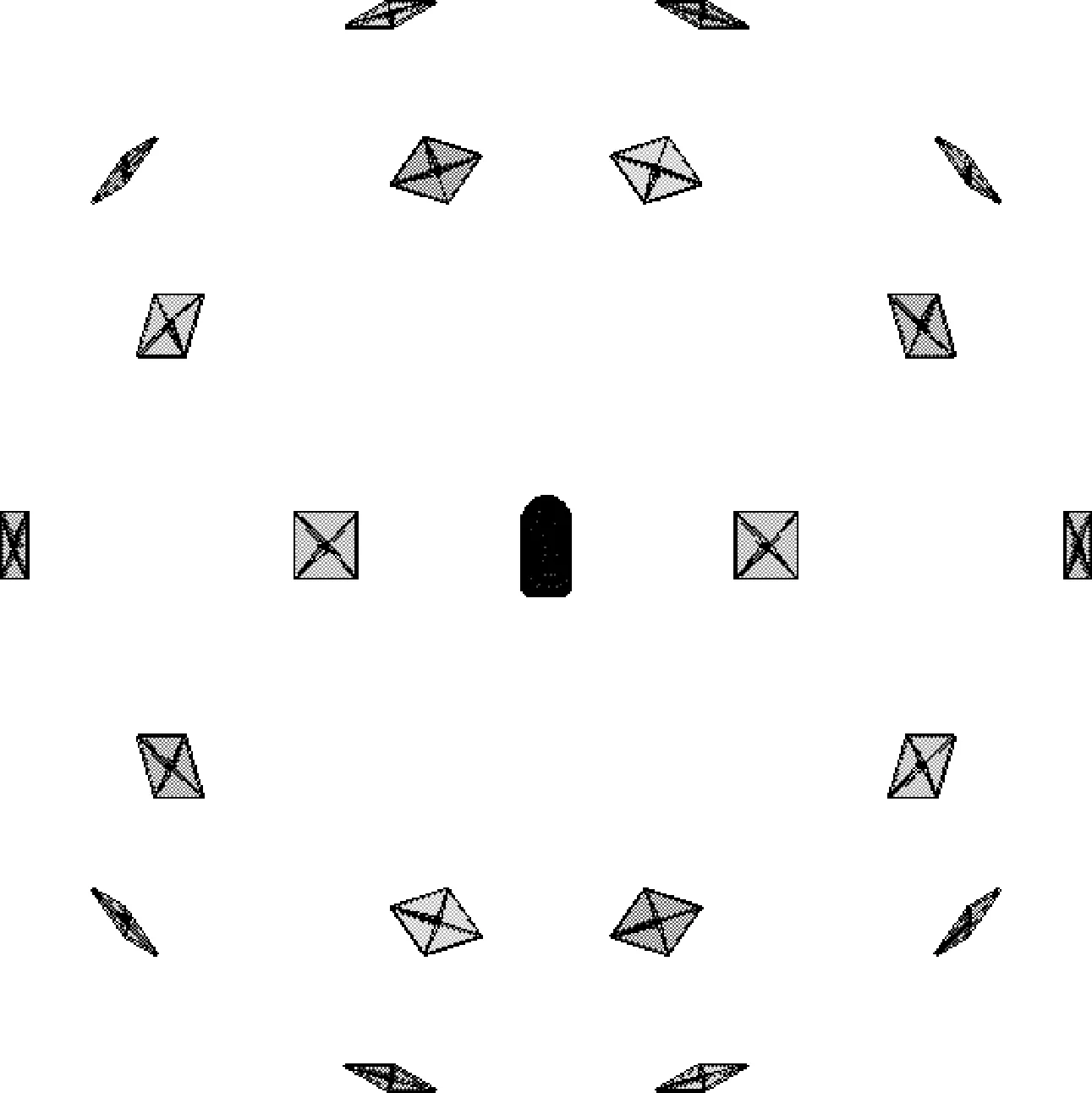
圖2 分布式平面波示意圖Fig.2 Schematic diagram of distributed acoustic plane wave

由式(8)可知，當縮比模型的縮比比例為α時，聲源聲功率應變為原模型的α2倍，振動頻率變為1/α，整流罩的厚度變為α倍，聲源到整流罩內部的距離變為α倍。由相似律，計算頻率與振動頻率縮比比例相同，因此計算頻率范圍同樣變為1/α倍。整流罩的材料屬性為鋁，其密度為2700kg/m3,彈性模量70 GPa，泊松比0.3，阻尼比2%；將空氣簡化為理想媒介，聲波在其中傳播時不存在耗散，空氣聲速和密度分別設為346 m/s，1.185 kg/m3，在本文計算中均采用此參數。參照原模型，本文分別建立了1/2,1/3,1/4,1/5縮比比例的模型來分析對比。計算了原模型與縮比模型的內聲腔的響應和整流罩的壁面振動，其頻率范圍分別為10～300 Hz,20～600 Hz,30～900 Hz,40～1200 Hz和50～1500 Hz。

2.2 結果與對比

由于有效載荷通常位于整流罩圓柱段，建立圖3所示的場點網格來獲得整流罩內聲腔的聲壓級響應，長方形場點網格均勻分布在圓柱段內，由25個單元36個節點組成。對于縮比模型，其場點網格成比例縮小。

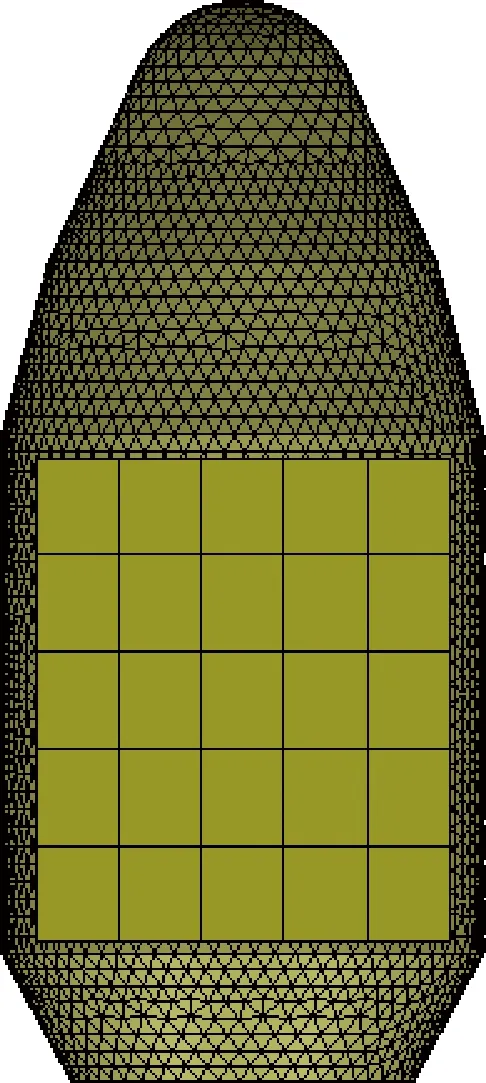
圖3 場點分布示意圖Fig.3 Schematic diagram of field points distribution

采用聲學有限元方法計算得出了原模型與縮比模型的場點聲壓級，使用聲壓均方根平均法將24個平面波激勵下的場點聲壓響應進行疊加，得到在混響激勵下的場點聲壓級。圖4為原模型與縮比模型的場點平均聲壓級曲線，圖5為場點峰值聲壓級曲線。由于原模型與縮比模型的計算頻率與圓柱段直徑的乘積是不變的，為便于對比，采用此方式來分析原模型與縮比模型的差異。聲壓均方根平均法的計算公式[17]為

(11)

式中：Li為場點的聲壓級，n為場點節點數。

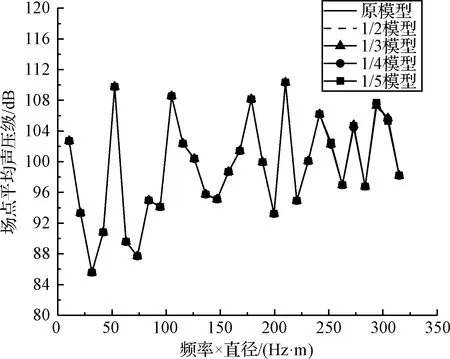
圖4 場點平均聲壓級Fig.4 Average sound pressure level of field points

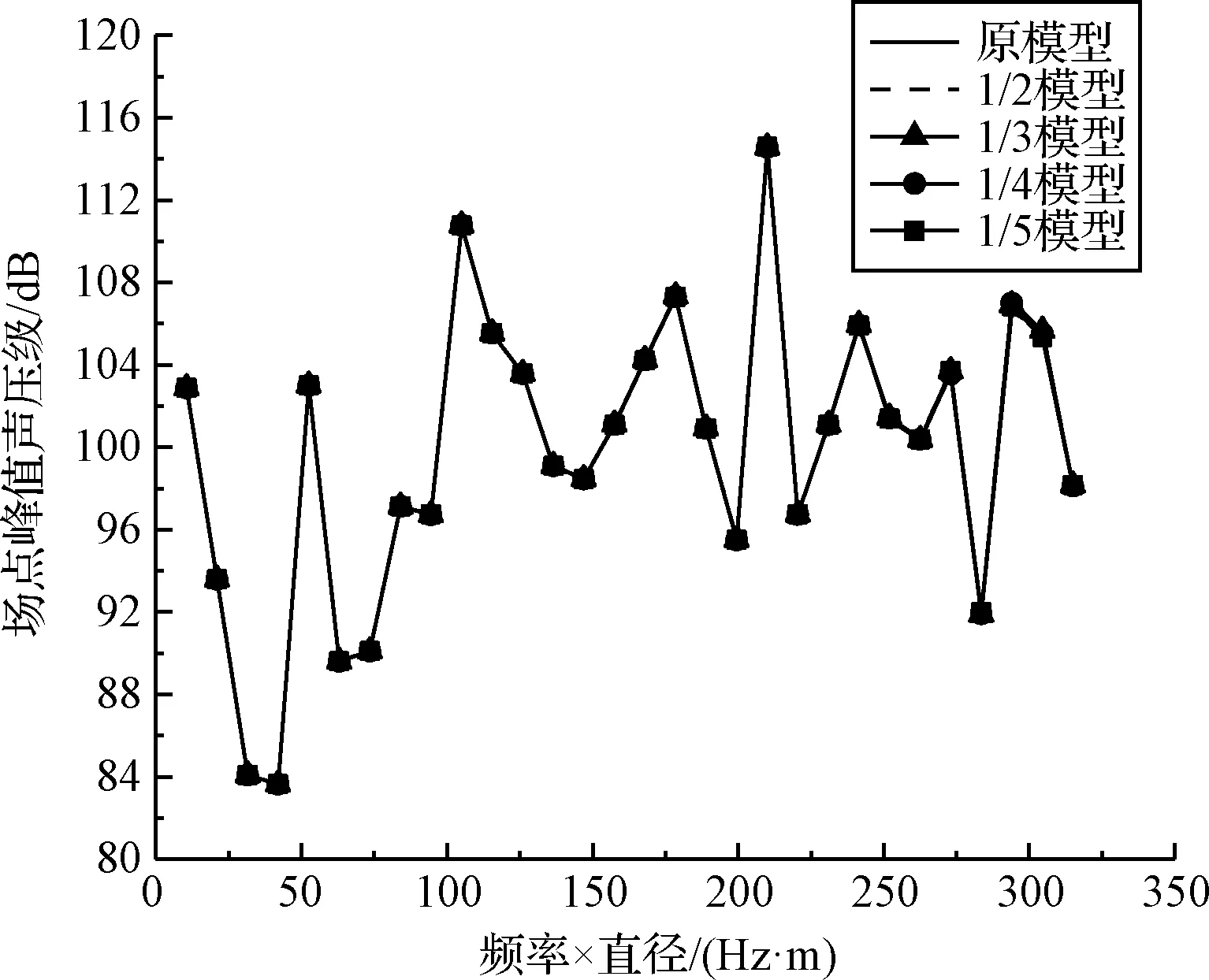
圖5 場點峰值聲壓級Fig.5 Peak sound pressure level of filed points

表1 原模型與縮比模型平均聲壓級對比Table 1 Comparison of average sound pressure level between the original model and the scaling models

為了定量地校驗縮比準則結果，以原模型為參考，分別取頻率為50 Hz,100 Hz,150 Hz,200 Hz,250 Hz處的場點聲壓級進行對比分析。式(8)表明，縮比模型整流罩內部場點聲壓級與原模型一致。表1表2為原模型與縮比模型的平均聲壓級、峰值聲壓級對比表，且給出了偏差值。

表2 原模型與縮比模型峰值聲壓級對比Table 2 Comparison of peak sound pressure level between the original model and the scaling models

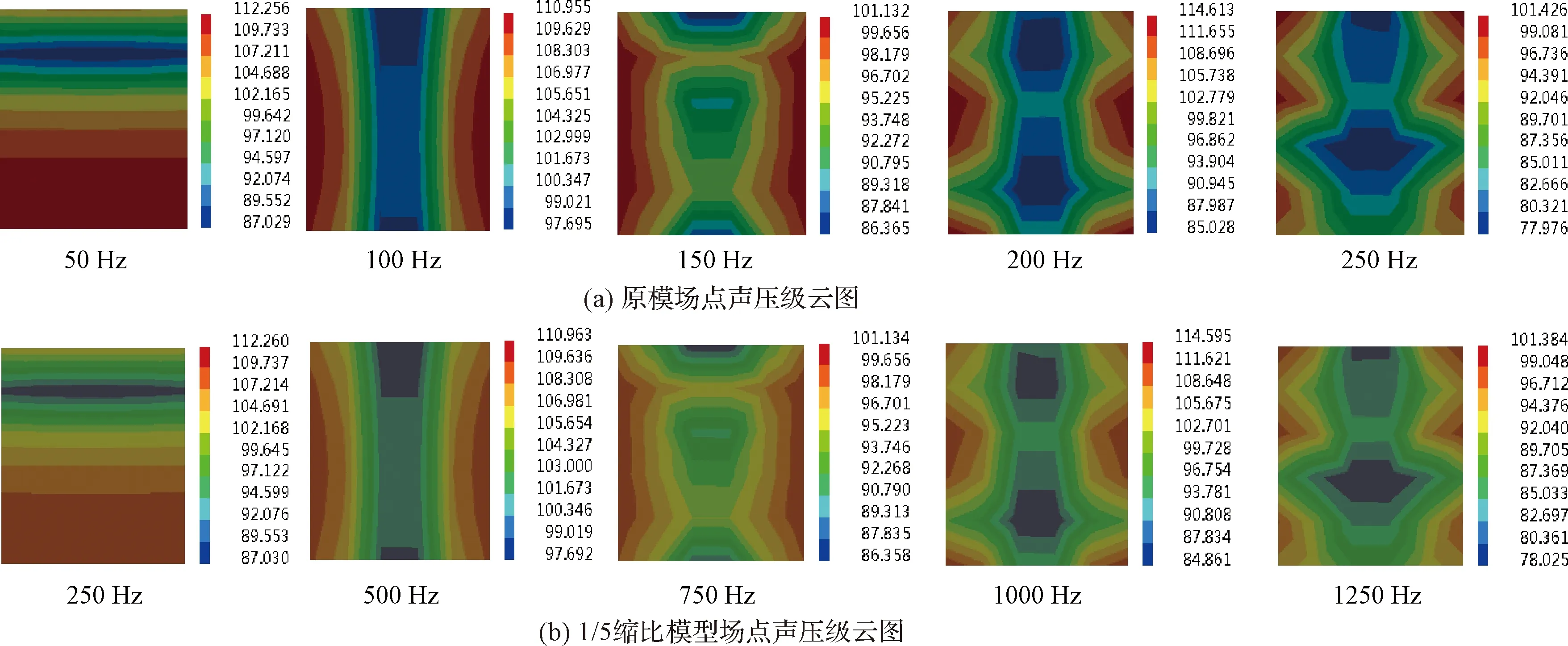
圖6 原模型與1/5縮比模型場點聲壓級云圖對比Fig.6 Comparison between sound pressure level of the original model and sound pressure level of the 1/5 scaling model

從表1、表2可以看出，原模型與縮比模型平均聲壓級在對應頻率上相同，最大相差0.04 dB，而峰值聲壓級最大相差0.09 dB。圖6為原模型與1/5縮比模型的場點聲壓級云圖對比，原模型與縮比模型在對應頻率上聲壓級分布相同，只在數值上有微小差別，校驗了縮比準則在聲壓級上的正確性。

圖7 整流罩樣本點位置Fig.7 The position of sample points

由于整流罩的呼吸變形對有效載荷的包絡空間影響較大[18]，選取了圖7所示整流罩縱向對稱面上的一系列樣本點，使用均方根平均法將24個平面波激勵下的樣本點徑向加速度響應進行疊加，得到混響激勵下樣本點的徑向加速度，研究整流罩結構上的振動情況是否滿足相似準則。獲得了原模型與縮比模型的徑向平均加速度曲線(見圖8)，圖9為徑向峰值加速度曲線。

同樣以原模型為參考，分別取頻率為50 Hz，100 Hz,150 Hz,200 Hz,250 Hz處樣本點徑向加速度進行分析對比。由式(10)可知，當縮比比例為α時，縮比模型整流罩壁面振動加速度為原模型1/α。表3、表4為原模型與縮比模型樣本點徑向平均加速度、峰值加速度對比表，誤差的計算公式為

|asca·α-a|/a

(12)

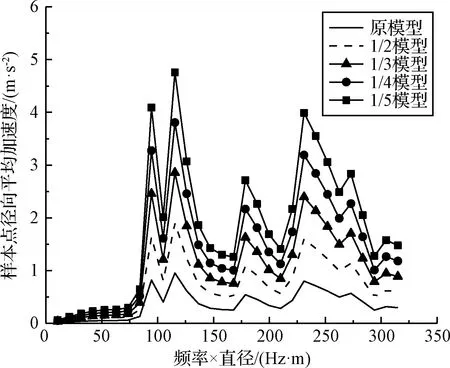
圖8 樣本點徑向平均加速度Fig.8 Average acceleration of sample points

從表3、表4可以看出，當縮比比例為α時，縮比模型與原模型樣本點徑向加速度在對應頻率上為1/α，樣本點徑向平均加速度最大誤差為0.98%，峰值加速度最大誤差為1.28%，在網格劃分等因素造成的誤差之內。圖10為原模型與1/5縮比模型的加速度云圖對比，可以看出縮比模型與原模型在對應頻率上加速度分布相同，縮比模型加速度為原模型的5倍，與理論分析所得的縮比特性一致。

圖9 樣本點徑向峰值加速度Fig.9 Peak acceleration of sample points

表3 原模型與縮比模型樣本點徑向平均加速度對比Table 3 Comparison of average acceleration at the field point between the original model and the scaling models

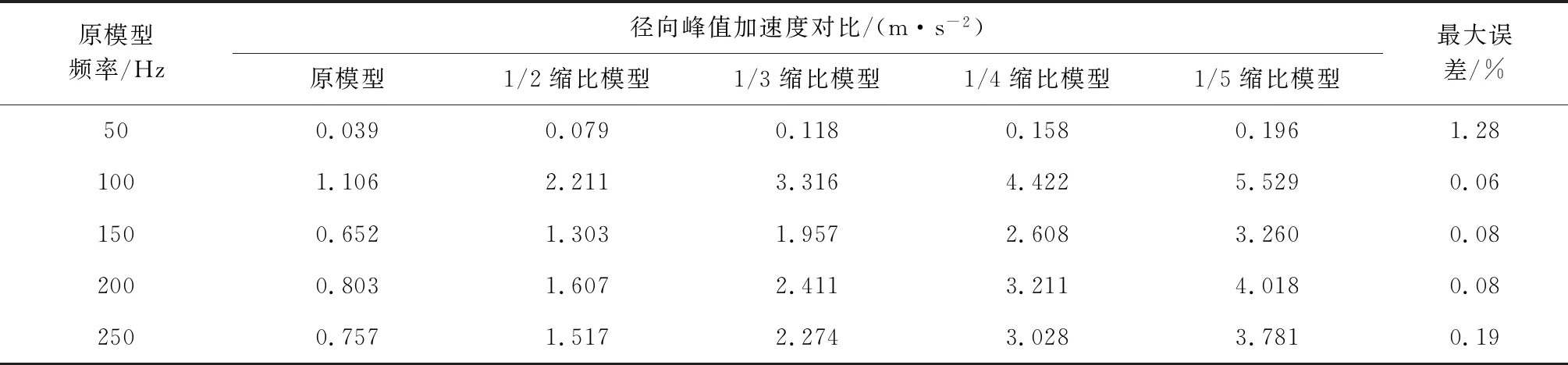
表4 原模型與縮比模型樣本點徑向峰值加速度對比Table 4 Comparison of peak acceleration at the field point between the original model and the scaling models

在仿真計算的過程中，雖然縮比模型尺寸較小，但其計算頻率范圍更廣，而計算頻率上限又與線性網格單元尺寸有對應關系[19]：

(13)

式中：L為單元長度，c0為聲音在介質中的傳播速度，fmax為最高計算頻率。

因此為了獲得較大的計算頻率上限，縮比模型的單元尺寸更小，從而網格數量與原模型相同。對于縮比模型的計算頻率范圍更廣的情況，增大計算頻率間隔從而使計算步數相同。由于縮比模型與原模型網格數量、計算步數相同，因此仿真時間也幾乎相同，從而在仿真中使用縮比模型并不能提高計算效率。但在聲振環境試驗中可以參考本文的縮比準

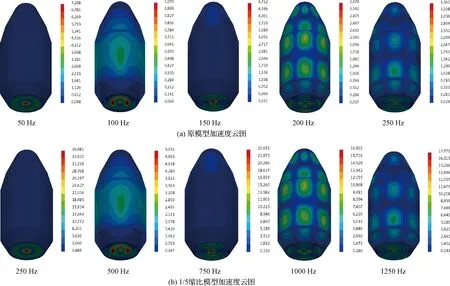
圖10 原模型加速度云圖與1/5縮比模型加速度云圖對比Fig.10 Comparison between acceleration of the original model and acceleration of the 1/5 scaling model

則設計縮比模型試驗。

3 結 論

以某火箭整流罩為研究對象，通過量綱分析以及聲學有限元仿真對不同縮比比例下整流罩內聲場、壁面振動加速度進行了研究，得出了縮比模型與原模型的比例關系，形成縮比準則，即在α2倍聲功率下，縮比模型內聲場與原模型一致，整流罩壁面加速度為原模型的1/α。結果表明，縮比模型與原模型保持較高的相似性，本文所推導的相似關系可以應用到聲振環境預示、聲振環境試驗中。

理論上講參考本文的縮比準則可設計任何縮比比例下縮比模型試驗，縮比倍數越大越節省費用，但在實際試驗過程中，縮比倍數越大，聲壓在單位尺度上的變化率越高，這將對試驗測試造成困難，增大試驗誤差，而且隨著縮比倍數增大，整流罩厚度越薄，一方面不利于加工制造，另一方面可能會使材料的強度等參數發生變化，因此在實際縮比試驗中應當合理選擇縮比比例。