三維攻擊角度約束部分制導控制一體化設計

賴 超，王衛紅，周本春，周星合，林大鵬

(1. 北京航空航天大學自動化科學與電氣工程學院，北京 100191；2. 中國艦船研究院，北京 100101)

0 引 言

基于頻譜分離的假設，傳統的導彈制導與控制系統分開獨立設計以其優良性能已經成為一種廣泛使用的重要方法。然而，在末制導階段，當目標速度較大并有較強的機動時，隨著彈目距離減少，制導回路的時間常數變小，帶寬隨之變大，頻譜分離假設不再成立，導致脫靶量增大甚至攔截器失穩等問題。為了解決這個問題，文獻[1]將制導系統與控制系統進行整體設計，首先提出了制導控制一體化(Integrated guidance and control, IGC)的設計方法。IGC設計將制導系統與控制系統合并到一個統一的架構中，進而利用彈目相對運動動態與導彈自身運動動態直接產生舵偏控制量。通過充分利用兩個系統間的協同關系，IGC已經成為提高攔截性能的潛在解決方案[2]。近年來，許多不同的控制方法應用于IGC設計，取得了更高的制導性能，例如自抗擾控制[3]，反步法[4]，動態面控制[5]與滑模控制[6]等。然而，已有學者指出：不能充分利用導彈轉動動態與平移動態之間的固有時間尺度分離特性是IGC設計的重要局限性[7]。導彈轉動動態通常快于平移動態，IGC通過平移運動誤差直接產生舵偏，傾向于導致轉動動態的不穩定。尤其當目標進行快速大機動時，系統轉動動態更容易不穩定，從而導致攔截精度下降，也增加了一體化調參的難度。

為了改進IGC設計的不足，部分制導控制一體化(Partial integrated guidance and control, PIGC)方法被提出來[7]。PIGC設計結合傳統獨立設計與IGC設計的優勢，采用雙回路控制器結構：外回路通過利用制導系統與控制系統的耦合信息，產生期望的角速度指令以保證攔截；內回路跟蹤角速度指令，并生成控制舵偏。PIGC不僅擁有提高制導性能的潛力，而且使轉動運動更加穩定，因而得到了學者們的廣泛關注。文獻[8]提出了一種自適應非奇異終端滑模控制方法并將其用于俯仰通道的PIGC設計。同樣在俯仰通道，針對迎向機動目標的攔截問題，文獻[9]引入擴張狀態觀測器來估計目標未知加速度信息，并基于此進行了PIGC設計。進而，考慮更多的實際約束的俯仰通道PIGC方法被提出來。文獻[10]運用終端滑模控制方法進行PIGC設計，達到了攻擊角度約束下的直接碰撞殺傷攔截。考慮到執行機構故障與飽和問題，文獻[11]引入輔助動態，進行了PIGC設計。在以上文獻中，PIGC設計取得了優良的制導性能。然而，以上文獻均集中在二維PIGC設計，尤其是俯仰通道的PIGC設計上，對三維PIGC設計的研究不多。

為了最大限度地利用導彈三通道間耦合關系，研究三維PIGC設計尤為重要。考慮三維攔截幾何動態，文獻[12]使用模型預測控制與動態逆控制方法提出了三維PIGC設計方法。同樣采用模型預測控制，文獻[13]針對高速彈道導彈目標的攔截問題，設計了三維PIGC方法。然而，文獻[12-13]針對的都是沒有機動的目標，因此算法設計中無需考慮目標位置加速度信息造成的不確定性。同樣地，考慮三維攔截幾何動態，文獻[14]提出了自適應多輸入多輸出(MIMO)滑模控制，并進行了帶攻擊角度約束的PIGC設計，完成了三維空間中的兩個攻擊角度約束下的精確攔截。在模型推導中，體軸角速度應該合并為一項并作為外回路控制量。然而，文獻[14]沒有考慮控制律中直接使用的導彈速度微分體軸系分量中含有外環控制量體軸角速度，沒有將其合并入控制項中。因此，速度微分體軸系分量會在一定程度上影響控制性能，盡管已經假設其可得。本文充分利用攻角、側滑角、體軸角速度與導彈速度微分體軸系分量的關系，建立了STT導彈嚴格反饋形式的PIGC設計模型，且不需要導彈速度微分體軸系分量。另外，帶有攻擊角度約束的制導律能有效增加彈頭殺傷力。因此，研究帶有角度約束的三維PIGC設計有重要意義。

本文針對“地對空”STT導彈迎面攔截機動目標的場景，提出了帶有攻擊角度約束的三維部分制導控制一體化設計方法。首先，通過充分利用制導系統與控制系統之間的協同關系，建立了針對機動目標攔截的STT導彈的三維PIGC設計模型，且不需要導彈速度微分體軸系分量信息。然后，通過使用終端滑模思想構建動態面方法的誤差向量與虛擬控制量，實現攻擊角度約束下的精確攔截。同時，引入有限時間收斂擴張狀態觀測器(Extended state observer,ESO)估計系統不確定性，并設計自適應算子與自適應律對觀測器的估計誤差進行補償，提高算法的魯棒性。綜合以上，提出了一種基于自適應終端滑模動態面控制方法(ATDSC)的三維PIGC設計。最后，數字仿真結果校驗了方法的有效性。

1 模型闡述

1.1 三維部分制導控制一體化設計模型

PIGC采用雙回路設計結構：外回路利用制導與控制系統之間的耦合關系，以彈體系角速度作為控制量以保證攔截；內回路以舵偏作為控制量，跟蹤外回路產生的期望角速度。建立PIGC外回路與內回路設計模型如下所述。

1)外回路設計模型

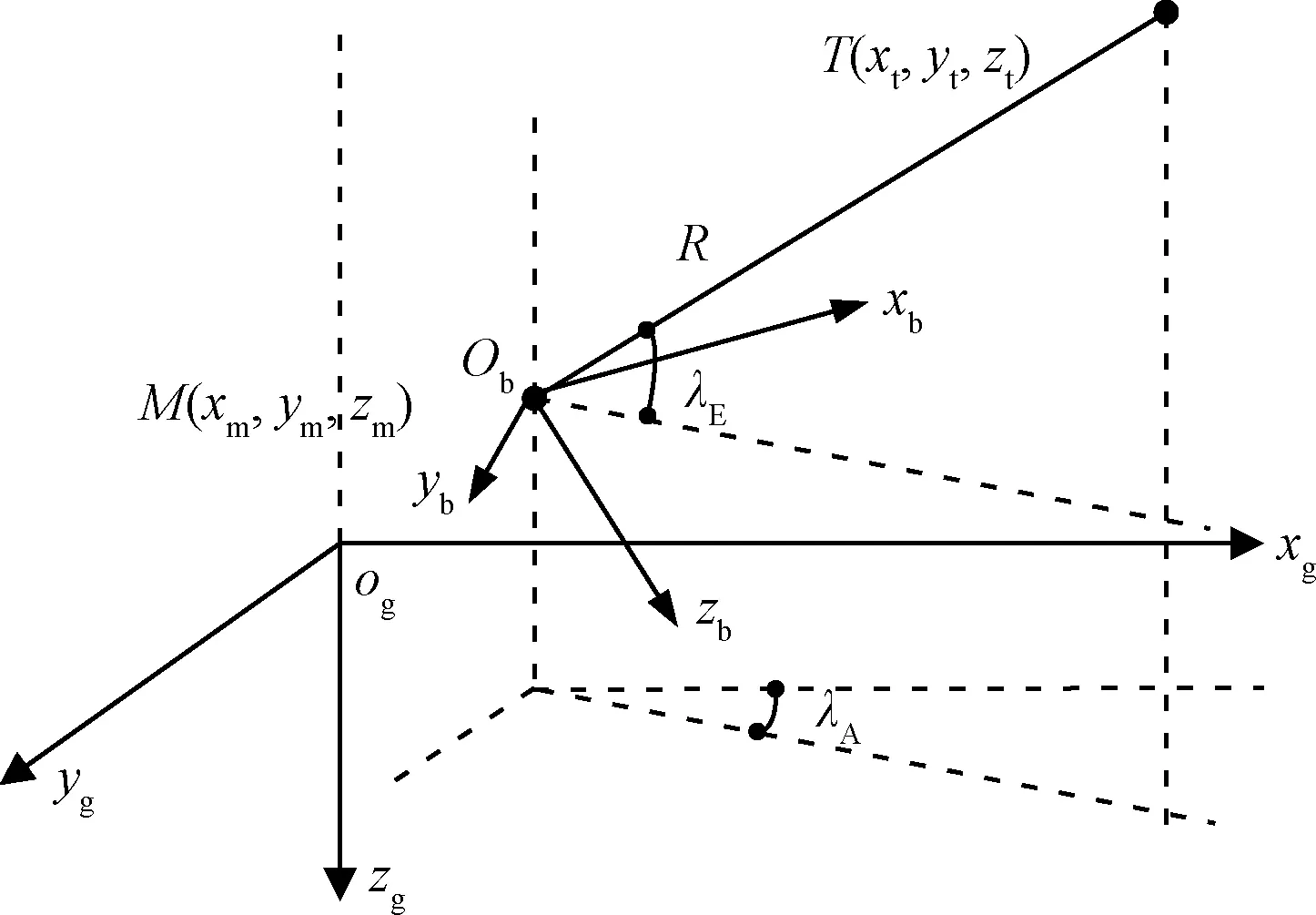
圖1 三維攔截幾何關系圖Fig.1 Interception geometry in three-dimensional space

首先，三維攔截幾何關系如圖1所示，其中，Ogxgygzg表示慣性系，Obxbybzb表示體軸系，M(xm,ym,zm)與T(xt,yt,zt)是導彈與目標的位置坐標，λE與λA表示彈目視線傾角與偏角，R表示彈目相對距離。

依據文獻[14]建模的方法，通過對圖1建立的坐標系對應的攔截動態方程求導，得到視線角的二階微分方程，如下所示：

(1)

通過坐標系轉換關系，可以得到：

(2)

式中：S11=cosθcosψ,S12=sinθcosψsinφ-sinψcosφ,S13=sinθcosψcosφ+sinψsinφ,S21=cosθ·sinψ,S22=sinθsinψsinφ+cosψcosφ,S23=sinθ·sinψcosφ-cosψsinφ,S31=-sinθ,S32=cosθ·

sinφ,S33=cosθcosφ,u，v，w表示彈體系速度分量，θ，ψ，φ表示俯仰角、偏航角與滾轉角，Sθφφ為彈體系和慣性系之間的轉換矩陣。對式(2)求導并進行化簡，可得：

(3)

式中：

L11=-usinθcosψ+vcosθcosψsinφ+wcosθcosψ·cosφ,L12=-ucosθsinψ-v(sinθsinψsinφ+

cosψcosφ)-w(sinθsinψcosφ-cosψsinφ),

L13=v(sinθcosψcosφ+sinψsinφ)-w(sinθ·

cosψsinφ-sinψcosφ),L21=-usinθsinψ+

vcosθsinψsinφ+wcosθsinψcosφ,L22=ucosθ·

cosψ+v(sinθcosψsinφ-sinψcosφ)+w(sinθ·

cosψcosφ+sinψsinφ),L23=v(sinθsinψcosφ-cosψsinφ)-w(sinθsinψsinφ+cosψcosφ),

L31=-ucosθ-vsinθsinφ-wsinθcosφ,L32=0,L33=vcosθcosφ-wcosθsinφ。

導彈的運動方程組如下：

(4)

式中：p，q，r為滾轉、俯仰與偏航角速度。

導彈的力方程組如下所示：

(5)

式中：m為導彈質量，g為重力加速度，Fx,Fy,Fz為氣動力，并且可以表示為[14]：

(6)

式中：dx,dy,dz為不確定性，cx,cy,cz,cx0,cyβ,czα為空氣動力系數，α與β為攻角與側滑角，ρ為空氣密度，Vm為導彈速度，kF為取決于導彈外形的常量。

將式(3)～(6)代入式(1)，并進行計算與化簡：

(7)

式中：dE與dA為包含目標加速度信息以及dx,dy,dz的系統不確定性。本文研究STT導彈攔截迎向機動目標，有如下假設：

假設1. STT導彈關于y軸與z軸對稱，即Iyy=Izz,Ixy=Iyz=Izx=0，其中Iyy與Izz為導彈繞y軸與z軸的主慣量，Ixy,Iyz,Izx表示導彈的慣量積。

根據假設1,力矩方程組如下：

(8)

其中，L,M,N為滾轉、俯仰與偏航力矩，可以表示為：

(9)

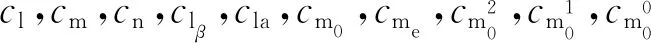
通常情況下，STT導彈在整個飛行過程中，滾轉角保持在一個固定值。依據文獻[14]，滾轉通道控制設計為：

(10)

式中：δa為滾轉舵偏，Ixx,Iyy,Izz為相應轉動慣量，cla與clβ為氣動系數，φref為期望滾轉角，kr1與kr2為控制參數。選擇合適的kr1與kr2，滾轉角將保持在期望滾轉角，即p=0,φ=φref，證明見文獻[14]。因此，有以下假設：

假設2[14]. STT導彈滾轉通道穩定(p=0)，并且滾轉角保持在期望滾轉角(φ=φref)。

考慮假設2，取φref=0，考慮式(7)，并結合攻角與側滑角微分方程[14]，得到具有嚴格反饋形式的PIGC外回路設計模型如下所示：

(11)

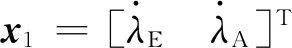
cosλEsinθ],

(cosαcosθcosφ+sinαsinθ),

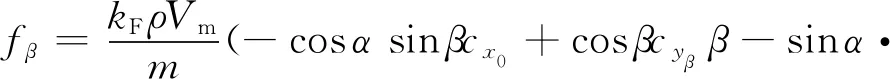
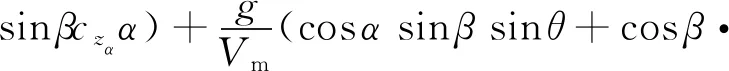
cosθsinφ-sinαsinβcosθcosφ),

注1. 充分考慮攻角與側滑角，體軸角速度與導彈速度微分體軸系分量關系，建立了具有嚴格反饋形式的PIGC外回路設計模型。與文獻[14]相比，不再需要導彈速度微分體軸系分量信息。

假設3. 模型不確定性D1與D2可微且有界，參數矩陣G1(x1)可逆且范數有界，并且，系統狀態均可獲得。

2)內回路設計模型

考慮假設2，結合式(8)～(9)，內回路模型為：

(12)

1.2 目標模型

采用的機動目標模型如下所示：

(13)

式中：xt,yt,zt為目標位置坐標，θt,ψct為目標航向傾角與偏角，gp,gy表示目標俯仰與偏航方向加速度，Dt為阻力，g為重力加速度，Vt表示目標速度。其中，gp,gy,Dt,θt,ψct不可知，Vt,xt,yt,zt可知。

2 帶有攻擊角度約束的部分制導控制一體化設計

本節進行帶有攻擊角度約束的三維PIGC設計。PIGC雙回路設計結構如圖2所示：外回路使用體軸系角速度作為控制輸入以保證攔截，使用高階滑模(High-order sliding mode, HOSM)微分器來估計角速度指令的導數，內回路跟蹤外回路產生的角速度指令，并保證導彈轉動運動的穩定。

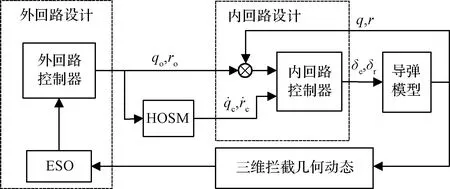
圖2 PIGC雙回路設計框圖Fig.2 Two-loop design sketch of PIGC

2.1 外回路設計

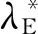
(14)

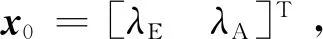
(15)

自適應終端滑模動態面控制(ATDSC)分為兩步進行設計，第一步得到虛擬控制量x2c，第二步得到真正的控制量uw。設計過程如下所示：

(16)

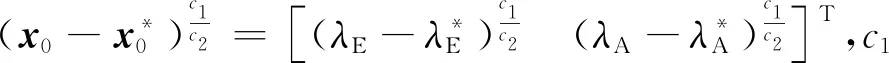
根據文獻[16]，構建二階非線性擴張狀態觀測器(Nonlinear extended state observer, NESO)來估計不確定性D1，如下所示：

(17)

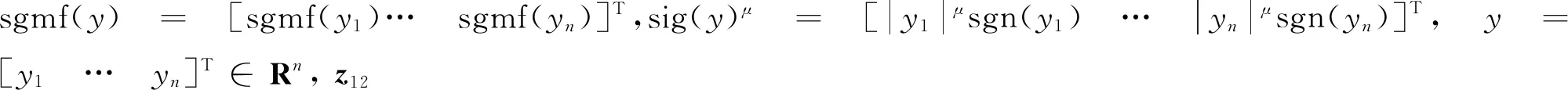
(18)

其中，ζ>0,τ>0

虛擬控制律設計為：

(19)

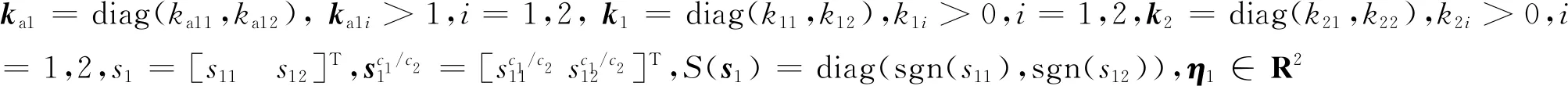
(20)

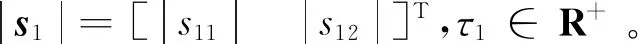
(21)

第二步：構建第二個誤差向量如下：

s2=x2-x2c

(22)

構建二階NESO來估計不確定性D2，如下所示：

(23)

式中：參數滿足ρ21>1,ρ22>1。

設計控制律如下所示：

ka2S(s2)η2-z22]

(24)

式中：ka2=diag(ka21,ka22),ka2i>0,i=1,2,k3=diag(k31,k32),k3i>0,i=1,2，s2=[s21s22]T,S(s2)=diag(sgn(s21),sgn(s22)),η2∈R2為自適應算子。設計自適應律，如下所示：

(25)

注2. 考慮到假設3，可以使用NESO來估計系統不確定性并且估計誤差可以實現有限時間收斂。文獻[17]指出，如果ESO的估計誤差可以有限時間收斂，則觀測器設計滿足分離定律。因此，通過選擇合適的參數，式(17)與式(23)的NESO相對于控制器可以進行獨立設計，并且，在穩定性分析中，將NESO的估計誤差當作有界誤差處理。

定理1. 滿足假設1～3，考慮非線性嚴格反饋系統式(11)，如果采用如式(16)～(25)的控制律，并且控制器參數滿足

(26)

式中:μ>0,μ∈R且I為單位陣，則系統誤差變量Si,p=x2c-x2d與ξi-ηi(i=1,2)一致最終有界。

證. 誤差向量p=x2c-x2d，結合式(15)～(16)與式(19)，得到s1的導數如下：

F1(x1)+G1(x1)(s2+p+x2d)+D1=

D1-z12+G1(x1)(s2+p)

(27)

結合式(15)、式(22)與式(24)，得到s2的導數如下：

(28)

根據式(21)，得到p的導數如下：

(29)

令D1-z12=[dz11dz12]T與D2-z22=[dz21dz22]T表示NESO估計誤差，則根據注2，滿足：

(30)

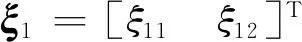
定義如下李雅普諾夫候選函數：

(31)

對式(31)求導得：

(32)

將式(20)、式(25)與式(27)～(29)代入式(32)，進行化簡，可得：

(33)

令ηi=[ηi1ηi2]T,i=1,2，得到以下不等式：

(34)

根據Young不等式，可得不等式如下所示：

(35)

將不等式(34)～(35)代入式(33)，可得：

(36)

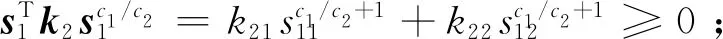
(37)

式中：H為常量，如下所示：

(38)

選取控制參數滿足條件

(39)

式中：μ>0,μ∈R，則式(37)可以推導為：

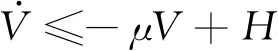
(40)

求解式(40)，可得：

V(t)≤V(0)e-μt+H/μ(1-e-μt)

(41)

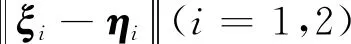
注3. 如果視線角速度收斂到0，則導彈與目標相對速度向量在垂直于彈目視線方向上的分量為0，即彈目相對速度完全落在彈目視線上，因此可以保證彈目距離一直減小，從而完成對目標的攔截。

注4. 針對STT導彈迎面攔截機動目標的場景，根據文獻[14]將視線傾角與視線偏角定義為攻擊角度，通過選擇合適的期望角度，保證攔截彈從目標的某一特定方向進行攔截，一定程度上避免尾追式攔截，增大攔截概率，同時，也便于導引頭截獲和穩定跟蹤目標。

注5. 自適應終端滑模動態面算法中，使用終端滑模思想構建第一個誤差向量并設計第一步的虛擬控制律，以達到精確攔截與攻擊角度約束的控制目的。

注6. 提出的自適應算子與自適應律用于補償NESO的估計誤差以增加算法的魯棒性。已有文獻指出[18]，自適應更新律中的絕對值項會使自適應算子隨著控制時間不斷變大，容易導致自適應算子過大影響穩定性。本文通過在自適應更新律中引入比例收斂項，避免了自適應算子的無限度增大，一定程度上，增強了系統的穩定性，并且，基于李雅普諾夫理論，證明了系統的穩定性。

2.2 內回路設計

采用超曲滑模控制方法用來進行內回路設計以達到有限時間收斂[19]。定義誤差向量：

(42)

對式(42)求導，得到：

(43)

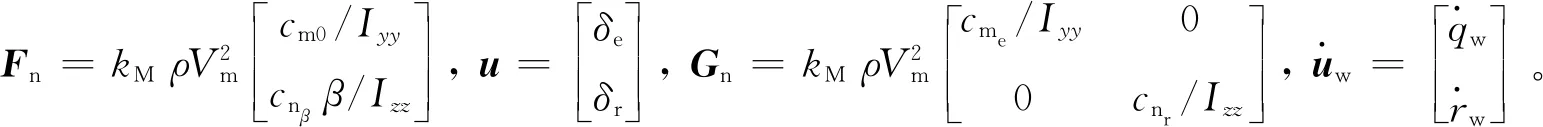
控制律如下所示：

(44)

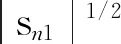
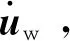
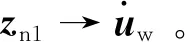
(45)

3 仿真校驗

本節進行了STT導彈攔截迎向機動目標的仿真，以校驗所提出方法的有效性。氣動系數的名義值如表1所示。

仿真中，空氣密度按照公式ρ=1.225(1-|zm|/44300)4.2533進行變化，其中|zm|表示飛行高度。導彈的參數為：1) 轉動慣量：Ixx=1.6151 kg·m2,Iyy=136.2648 kg·m2，Izz=136.2648 kg·m2；2) 質量：m=500 kg；3) 速度向量體軸分量：u(0)=400 m/s,v(0)=500 m/s，w(0)=-600 m/s；4) 幾何常數：kF=0.0143 m2,kM=0.0027 m3；5) 重力加速度：g=9.81 m/s2；6) 導彈初始位置：xm(0)=0,ym(0)=0,zm(0)=-3000 m；7) 舵偏量飽和值設置為35°。仿真中，攔截目標的參數為：1) 速度：Vt=600 m/s；2) 目標位置初始值：xt(0)=8000 m,ym(0)=8000 m,zm(0)=-11000 m；3) 初始航向傾角與偏角：θt=135°,ψct=-45°。

設計參數為：1) 控制參數：c1=1,c2=3,ks1=diag(1.5,1.5),ks2=diag(0.001,0.001),ka1=diag(0.05,0.10),k1=diag(2.0,2.0),k2=diag(0.02,0.03),σ=diag(0.01,0.005),τ1=0.2,k3=diag(2.0,2.0),ka2=diag(0.15,0.10),τ2=0.3；2) NESO參數：α1=0.7,ρ11=1.1,ρ12=1.1,ρ22=1.5,ρ22=2,kz1=1.5,kz2=1.2；3) HOSM參數：kd1=diag(10,10),kd2=diag(0.1,0.1)。

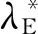
表2的仿真結果表明，在系統存在不確定性情況下，CDSC與ATDSC均能完成對迎向機動目標的攔截，一定程度上體現了擴張狀態觀測器對系統不確定性的補償作用。其中，相比于CDSC，ATDSC方法的脫靶量與攔截時間更小，取得了更好的攔截精度；ATDSC終端視線角的收斂誤差更小，取得了更好的角度收斂效果。

表1 氣動系數名義值Table 1 Nominal values of aerodynamic derivatives

表2 仿真結果Table 2 Simulation results

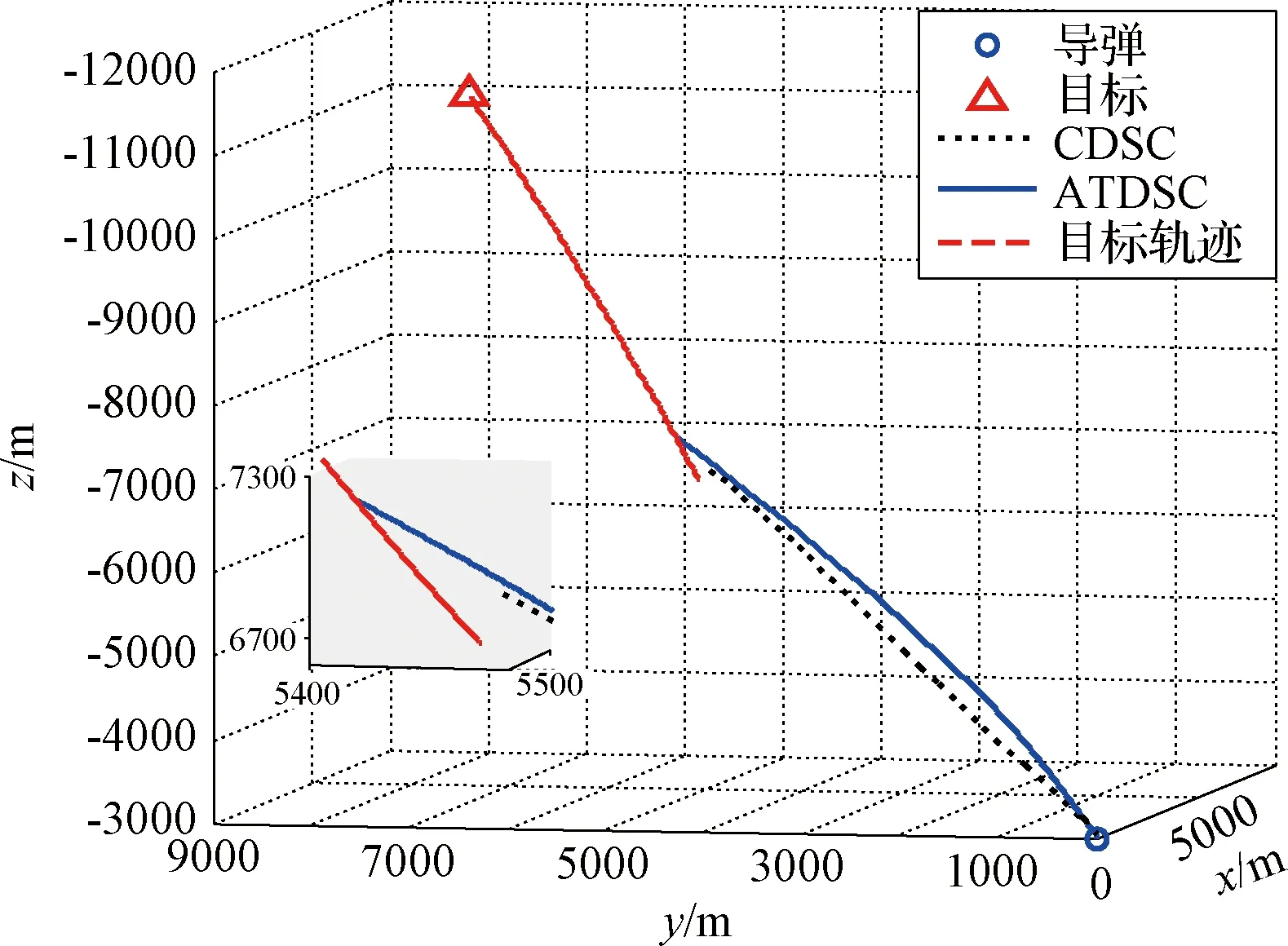
圖3 攔截軌跡Fig.3 Interception trajectories

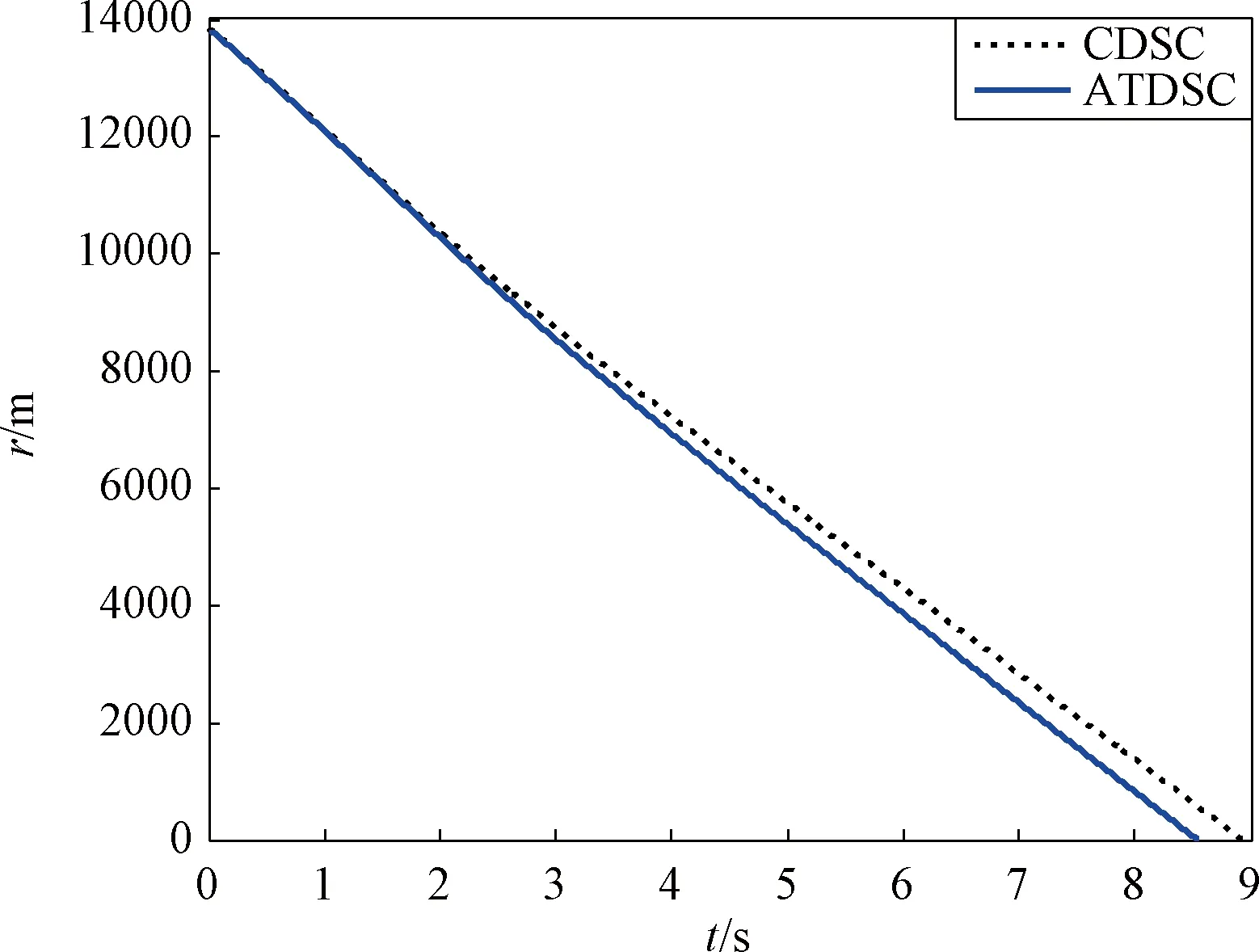
圖4 彈目相對距離Fig.4 Relative distance

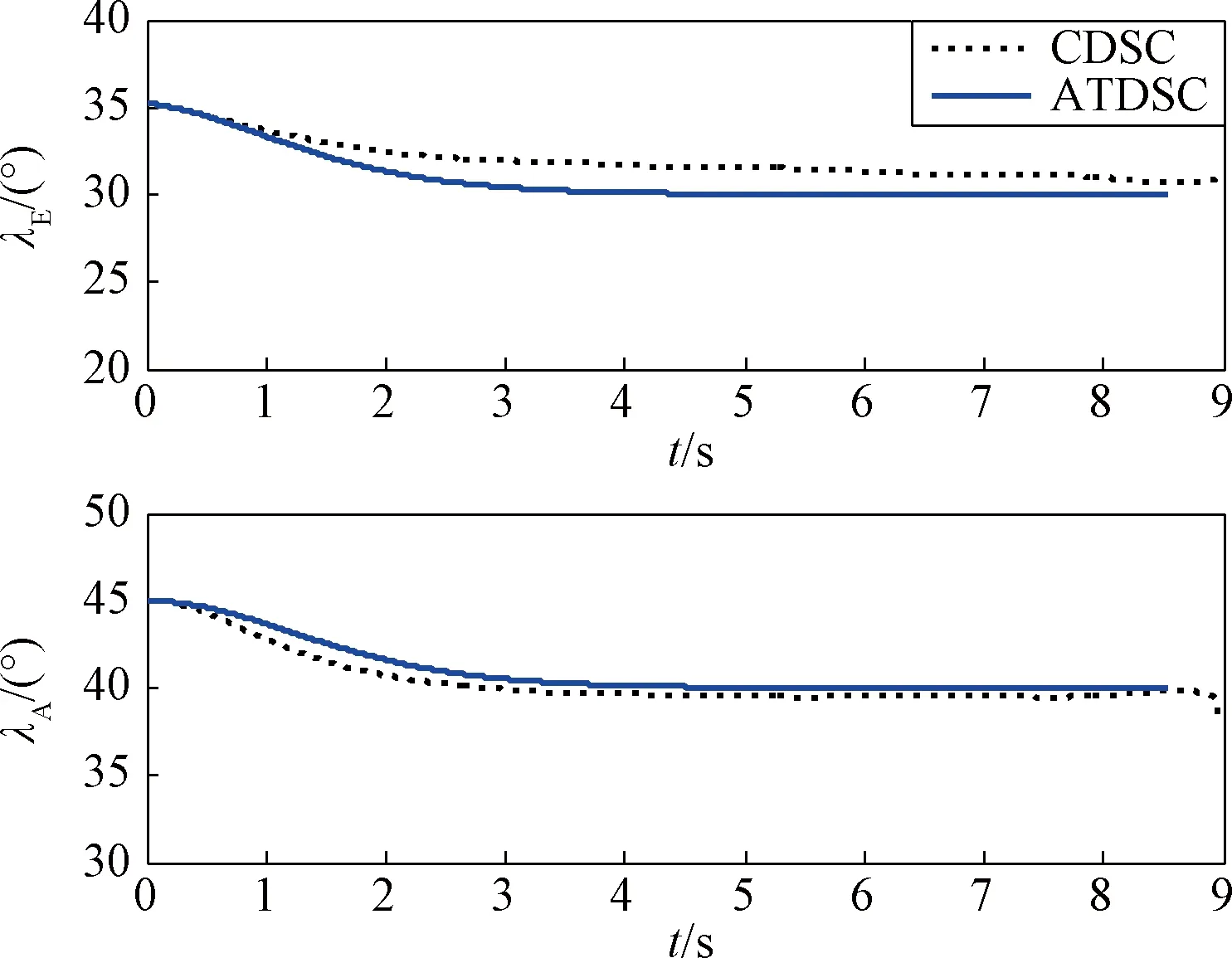
圖5 視線傾角與偏角曲線Fig.5 Curves of LOS elevation and azimuth angle

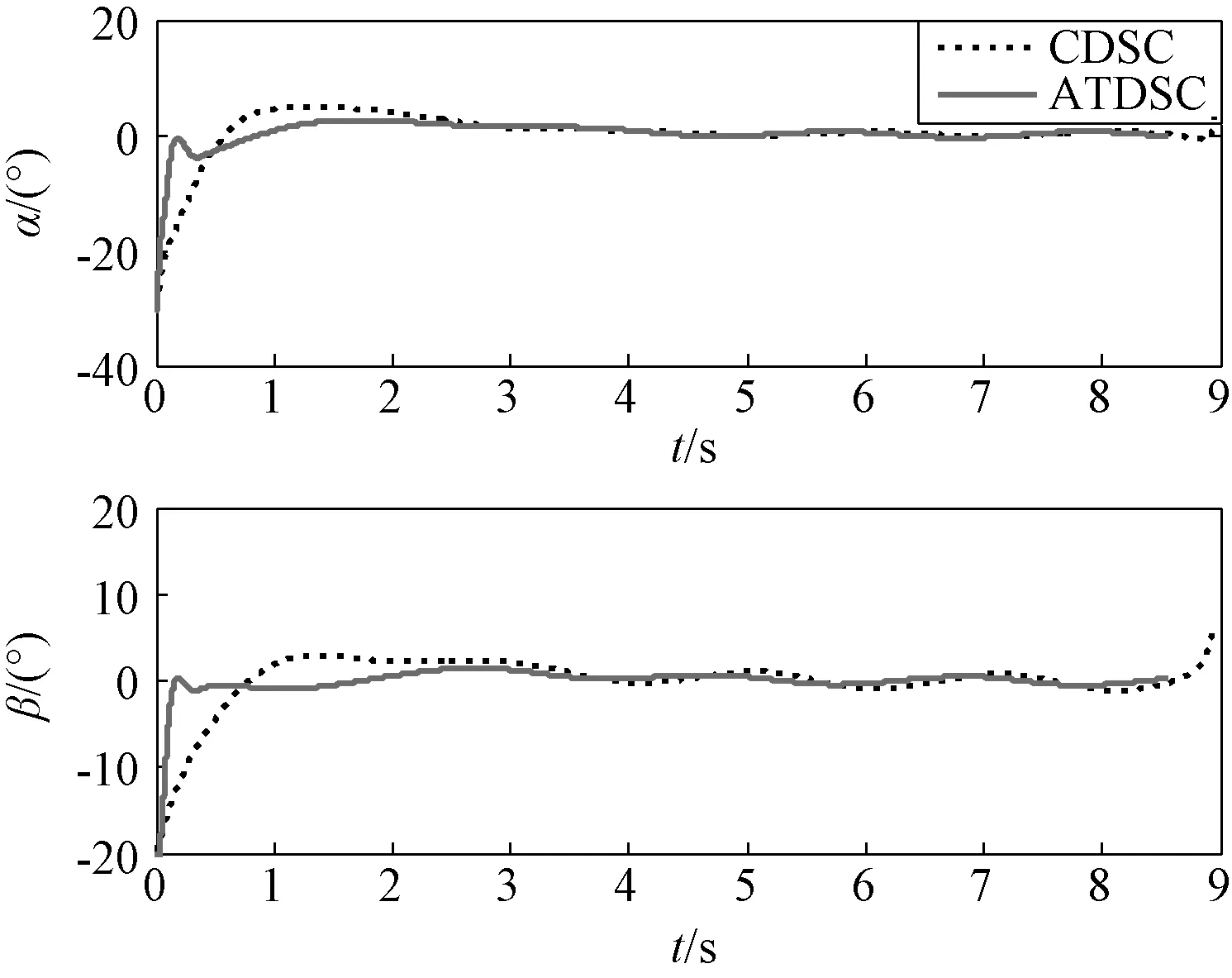
圖6 攻角與側滑角曲線Fig.6 Curves of attack angle and side slip angle

圖7 角速度曲線Fig.7 Curves of body rates

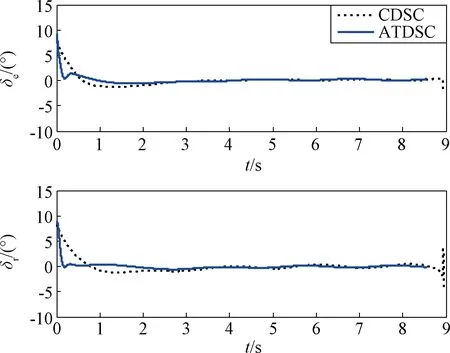
圖8 舵偏角曲線Fig.8 Curves of fin deflections

選擇表2第四行數據，仿真結果曲線如圖3～8所示。如圖3所示，ATDSC方法的彈道比CDSC更光滑、平直，因此攔截時間更短。如圖4所示，相比于CDSC的脫靶量(2.1932 m)與攔截時間(8.944 s)，ATDSC的脫靶量(0.0622 m)更小，攔截精度更高，并且攔截時間(8.553 s)更短。如圖5所示，CDSC和ATDSC的終端視線角分別為λEt=30.89°，λAt=39.84°與λEt=30.01°，λAt=39.99°。ATDSC能使視線角更快收斂到期望值，并且收斂精度更高。在ATDSC設計中，將第一個誤差向量設計為終端滑模形式，并據此設計第一步的虛擬控制量，因此在制導精度與攻擊角度約束收斂上達到更好的控制效果。如圖6～7所示，在整個攔截過程中，飛行狀態穩定并且有界，與定理相符。在圖8中，舵偏量沒有達到其舵偏飽和值35°。綜上所述，仿真結果說明，相比于CDSC，ATDSC取得了更高的制導精度與更好的攻擊角度收斂效果。

4 結 論

本文針對機動目標的帶有三維攻擊角度約束的攔截問題，建立了適用范圍更廣的STT導彈三維PIGC設計模型，并提出了一種基于自適應終端滑模動態面控制方法的三維攻擊角度約束PIGC設計方案。在未知目標機動加速度以及其他參數不確定性影響下，有效地實現了三維攻擊角度約束下的迎向機動目標精確攔截。使用李雅普諾夫理論證明了系統的穩定性，并且仿真結果校驗了方法的有效性。