空間目標三維重構誤差分析與相機參數設計方法

田 陽，宋 新，王 盈

(1. 哈爾濱工業大學深空探測基礎研究中心，哈爾濱 150080；2. 哈爾濱工業大學電子與信息工程學院，哈爾濱 150001；3. 上海宇航系統工程研究所，上海 201108)

0 引 言

隨著人類航天活動的日益頻繁，空間中故障失效的航天器也越來越多，以清理、維修失效衛星為目的的在軌服務技術逐漸成為研究熱點[1]，各航天大國紛紛開展了相關的技術研究和演示驗證計劃，如美國的FREND項目[2]，歐空局的TECSAS /DEOS項目[3]和日本的SDMR項目等[4]。在軌服務通常需對目標航天器進行繞飛監測、跟蹤接近、抓捕、對接、維修等操作，而準確獲取目標的三維模型，是判別抓捕部位、識別對接和維修部件的關鍵，直接決定了在軌服務的成敗。

目前獲取空間目標三維模型的方法主要有兩大類[5]:一類是利用激光雷達等主動設備直接對目標進行測量;另一類是利用光學相機等被動設備采集目標序列圖像，通過特征提取匹配、 運動恢復結構(Structure from motion,SFM)等技術重構目標三維結構[6]。由于在技術成熟度，獲取信息豐富程度和功耗等方面存在較大優勢，以光學相機為敏感器的被動方法仍然是主流。相關的研究也較為活躍，如光束平差法[7]，以及光束平差改進算法[8-9]，基于粒子濾波器或擴展卡爾曼濾波器的SLAM算法[10-11]，激光測距和慣性測量信息輔助圖像序列估計特征位置的方法等[1,12]。

利用圖像序列重構目標模型是一個2D-3D映射問題，需要進行一系列的算法處理，重構精度能否達到要求是任務設計者最為關心的問題之一，也是指導觀測方案設計和敏感器硬件選型的重要依據。Weng等[13]理論分析了特征點齊次坐標誤差對幀間運動估計和三維重構的影響。Grossmann等[14]針對基于極大似然和極大后驗估計的三維重構方法，研究了重構誤差傳播規律，給出了誤差的計算模型。文獻[15]分析了相機內參數誤差和特征匹配誤差對運動參數估計的影響。國內學者周凌翔等[16]假設三維點在圖像平面內的不確定性為正態分布，深度不確定性為均勻分布，建立了一種三維點不確定性描述模型，基于該模型給出了誤差估計方法。Min等[17]利用矩陣分析的方法給出了基礎矩陣的誤差計算方法，在此基礎上分析了三維點位置誤差。文獻[18]基于線性化的思想給出了三維點位置不確定性的快速計算方法。此外還有一類通過仿真試驗手段分析相機內外參數對重構誤差的影響。例如文獻[19]通過數學仿真分析了相機的焦距、積分時間及角速度對成像質量的影響；王澤斌[20]利用STK仿真軟件生成目標圖像，通過比較重構模型與真實模型評估觀測距離、抖動、拍照頻率、離焦量、積分時間及像元尺寸等參數對三維重建精度的影響。仿真試驗方法雖然可以分析確定重構精度，但只能針對特定已知目標，而對估算未知目標重構精度和指導重構任務方案設計意義不大。

在焦距、像素尺寸等相機內參數選取方面，文獻[21]針對無人機(UAV)采集圖像進行三維重構的任務，給出了相機參數選取方法，首先根據UAV飛行速度，圖像重疊區域百分比計算相機視場角，再由重構目標分辨率和視場角確定像素尺寸，最后根據UAV飛行高度給出相機焦距。陳宏宇等針對神舟七號伴飛觀測任務，從成像解析度需求出發，給出了寬、窄視場相機設計參數，并建立了觀測過程姿態控制方法[22]。類似的工作還有文獻[23]，根據火星著陸任務特點，設計了火星降落相機的幀頻、積分時間等參數。

在重構觀測方案設計方面，與之最為相關的研究領域為相機網絡設計(Camera network design,CND)，CND致力于在給定相機內參數基礎上，設計拍照時相機位姿，使重構不確定性或其它指標達到最優。CND研究主要思路有兩種，一種是以文獻[24]為代表的利用優化算法在限定狀態空間中搜索最優觀測序列；而另一種多與SLAM方法結合，在已經獲得初始重構結果的前提下，尋找下一次最優拍照位置[25]。

本文以空間目標三維模型重構為背景，首先梳理三維重構誤差傳播機理，給出三維重構誤差的計算方法；隨后通過分析計算，總結相機位置姿態等外參數與重構精度的關系，確定觀測距離與拍照間隔等觀測方案設計原則；最后給出根據重構精度指標反演相機焦距和像素尺寸參數的方法，并建立一套以重構精度為核心指標的觀測方案和相機參數設計方法。

1 空間目標三維重構誤差傳播機理分析

基于圖像序列重構空間目標三維模型一般包括以下幾個步驟：1)特征提取和匹配；2)根據相機內參數給出匹配特征點齊次坐標；3)根據齊次坐標值解算基本矩陣，并估計相機位姿參數；4)根據相機位姿和特征點齊次坐標解算特征點三維位置。圖1描述了三維重構誤差傳播規律，箭頭實線表示誤差傳播的路徑。可以看到，特征提取與相機內參誤差共同影響特征點齊次坐標；而特征點齊次坐標值作為三維重構算法的輸入，決定了相機外參數和三維重構的精度。這兩個過程彼此獨立，因此以特征點齊次坐標為分界線，分別討論誤差傳播的情況。

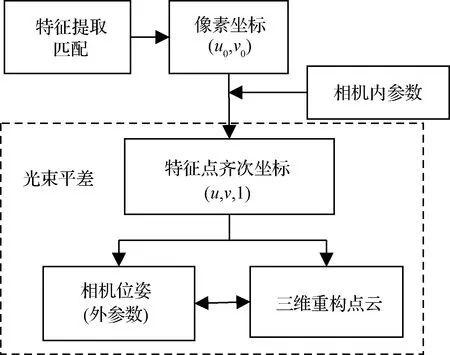
圖1 三維重構誤差傳播規律Fig.1 The illumination of 3D reconstruction error propagation

1.1 特征點齊次坐標誤差來源

首先分析相機內參數誤差對特征點齊次坐標的影響。根據相機小孔成像模型，特征點齊次坐標可表示為：

(1)

其中:u,v為包含鏡頭畸變影響的特征像素坐標，s為像素大小，f為相機焦距，u0和v0為成像平面中心坐標。假設s在發射和飛行過程中不受影響，而其他相機內參數f,u0和v0存在標定誤差，其標定值為f+Δf,u0+Δu0,v0+Δv0。在特征提取匹配和鏡頭畸變誤差共同影響下，特征點像素坐標為u+Δu，那么計算x軸齊次坐標時引入的誤差為

(2)

進一步整理可得

(3)

式中：s/f表示焦距歸一化后的像素尺寸，k=Δf/f為焦距誤差與真實值的比。對式(3)兩邊取絕對值以便估計其最大值，有

(4)

在式(4)中，齊次坐標誤差上限由三項組成。由于1+k≈1，因此可以認為每一項誤差值由分子決定，第一項為相機焦距f標定誤差對齊次坐標的影響，這一部分誤差和特征點位置相關，對齊次坐標影響最大；第二項為成像中心誤差的影響；第三項誤差由鏡頭畸變和特征匹配誤差共同組成。考慮到相機內參數可以在軌標定，且標定精度較高，如文獻[26]給出的標定方法可使焦距標定準確度優于1/10000，畸變系數準確度優于1%，因此在后續的分析中主要考慮無法消除的特征跟蹤誤差。已有研究成果表明，目前性能最好的SIFT特征提取與匹配算法[27]，對一般特征跟蹤誤差約為0.25個像素[28]。

1.2 空間目標三維重構誤差估算方法

利用光束平差法重構空間目標三維模型，一般采用如下性能指標函數

(5)

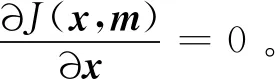
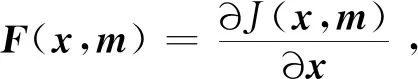
(6)

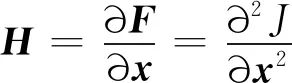
(7)

式中：Λm=diag(σ2,…,σ2)，這里認為所有特征點齊次坐標具有相同的觀測誤差方差σ2。本文假設在應用光束平差重構目標的過程中，以第一幀圖像對應的相機姿態為參考坐標系，位置為參考坐標系原點，三維點到參考坐標系原點平均距離為1，作為重構尺度約束，此時性能指標變為

(8)

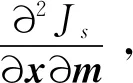
2 空間目標三維重構觀測方案設計原則

通過固定相機焦距、圖像分辨率、視場角等相機內參數，分析空間目標觀測距離、相機指向和拍照間隔等外參數與重構精度間的關系，給出以重構精度為核心指標的觀測方案設計原則。

第1.2節中已經給出了一種通過線性化手段近似光束平差法三維重構誤差的方法，但該估計結果與特征點觀測值相關，帶有一定的隨機性，更適合估算具體算例中的誤差方差。考慮到三維重構的本質是在一個參數估計問題，這里利用克拉瑪-羅(Cramer-Rao)不等式[29]，以式(8)為性能指標，給出參數估計誤差方差陣的下邊界，作為分析觀測距離、相機姿態和觀測間隔等參數與重構精度關系的工具。

利用克拉瑪-羅不等式計算重構誤差下界需要指定三維點位置，這里采用橢球體近似描述空間目標的三維結構，并在橢球面上選取一定數量三維點作為分析對象，如圖2所示。

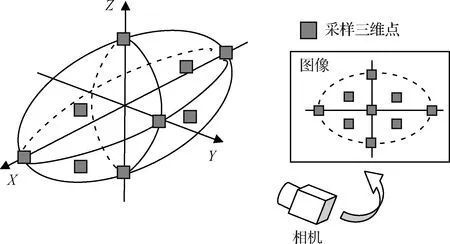
圖2 三維橢球面及選取的特征點Fig.2 Enveloping surface of space target and selected points

2.1 不同觀測距離重構精度分析

首先通過數值計算仿真分析觀測距離與重構精度之間的關系。相機內參數參照E2V公司的CCD230-84芯片設定為：像素尺寸15 μm，圖像分辨率為4096×4096。考察繞飛軌道高度100～500 m的重構誤差，為了保證在最低軌道高度下仍能夠采集空間目標的完整圖像，相機焦距設定為12.28 cm。拍照間隔為15°，即在繞飛圓軌道上每隔15°采集一幅空間目標圖像，共拍攝5幅圖像，相機光軸始終指向空間目標的中心。特征點跟蹤誤差標準差設定為0.25像素。代表空間目標的橢球體三軸設定為[20 m, 30 m, 20 m]，并在可見半球面選取9個點(如圖2所示)作為重構精度分析的采樣點。事實上使用特征點越多，重構精度越高，但在任務方案設計時，還無法有效估計特征點數量，因此這里僅選取基本覆蓋目標表面的9個采樣點保守計算重構精度，同時也可使計算量大幅度減少。

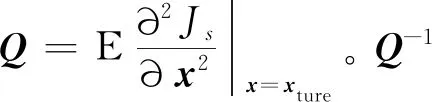
圖3 不同觀測距離下的三維重構誤差下限Fig.3 The limit of 3D reconstruction error at different distances

2.2 繞飛觀測過程姿態與重構精度的關系

相機參數、拍照間隔等仿真參數設定與第2.1節相同，但相機姿態控制采用兩種不同的策略，一是姿態保持慣性空間指向不變，另一種是相機光軸始終指向空間目標中心，比較兩種策略對應的重構誤差下限。

利用三維重構誤差下界數學模型，分別得到兩種策略對應的9個采樣點三軸重構誤差下限的平均值，如表1所示。

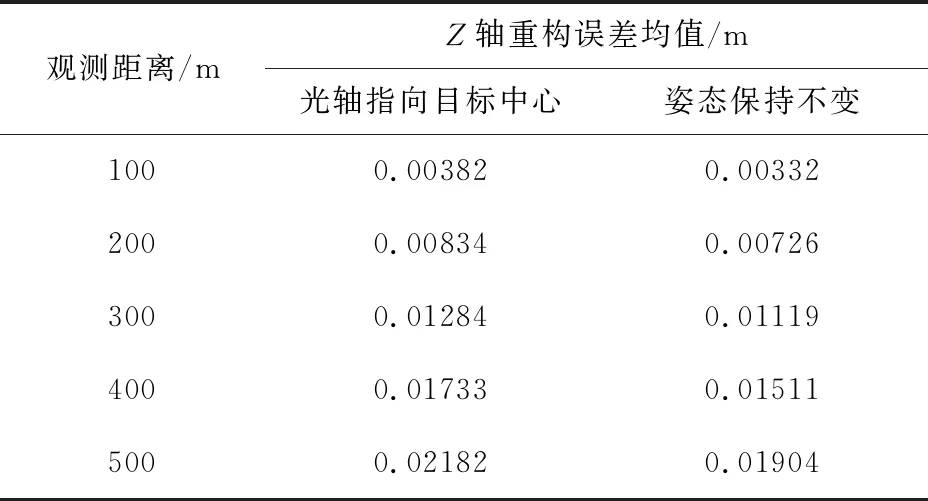
表1 不同姿態控制方案對應的采樣點重構誤差Table 1 3D reconstruction errors of different attitude control law

觀測距離由100 m增加至500 m過程中，均有姿態保持的重構精度略高于指向目標中心的結果，精度提高不超過13%。因此可以認為拍攝過程中姿態指向對重構誤差影響不大。為了保證繞飛過程中始終能夠采集到完整的目標圖像，相機應始終指向目標中心。

2.3 拍照間隔與重構精度的關系

分析不同拍照間隔對重構誤差的影響，相機參數設定與第2.2節相同，且相機光軸指向目標中心，但拍照間隔設定為15°和5°，分別采集3幅圖像，比較兩種拍照策略下的重構誤差下限。9個采樣點Z軸重構誤差下限的平均值如表2所示。均采集3幀圖像的前提下，拍照間隔為15°時，Z軸重構精度明顯優于拍照間隔為5°的情況。

改變仿真設定，在相同的總角度內，按照不同的拍照間隔采集圖像，即在30°的繞飛弧段內，以15°間隔拍攝3幀圖像，以5°間隔拍攝7幀圖像，由表2給出的重構誤差下限結果可以看出，以5°間隔拍攝7幅圖像的觀測方案Z軸精度有大幅度提高，略高于以15°為間隔的拍照方式。

綜合以上對觀測距離、姿控方案和拍照策略的分析，得到以下空間目標重構任務觀測方案設計原則：在相機內參數固定的條件下，應盡量靠近空間目標采集圖像；相機姿態對重構精度影響不大，為了保證目標圖像的完整性，應保持相機光軸始終指向目標中心；在特征跟蹤算法和遮擋關系允許的條件下，應盡量增加拍照間隔，或者選取拍照間隔較大的圖像作為重構算法的輸入。

3 空間目標三維重構相機內參數選取方法

根據式(5)和Fisher信息矩陣的定義不難發現，相機焦距、像素尺寸等參數是通過影響特征點齊次坐標誤差方差而影響重構誤差下限的。

(9)

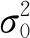
(10)

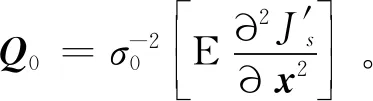
根據式(7)計算的重構誤差也可重寫為

(11)

可見k越大，特征點齊次坐標的誤差方差越大，重構誤差也就越大。因此，可以在確定觀測距離和拍照間隔這兩個主要觀測方案參數以后，通過選取滿足重構精度的k值計算焦距和像素尺寸。

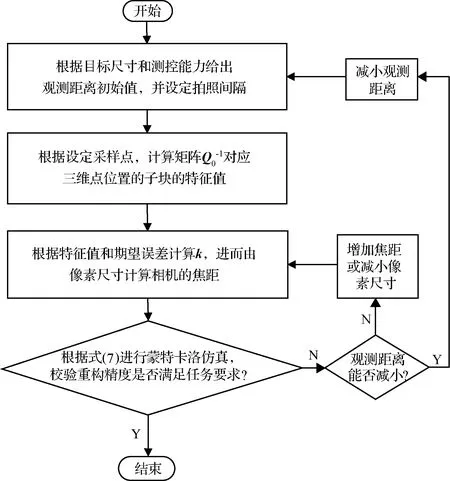
圖4 觀測距離和相機參數設計流程Fig.4 Observation distance and camera parameter design flow

綜合以上分析，以重構精度為指標的觀測方案和相機內參數設計流程如圖4所示。需要說明的是：所計算的子塊特征值是不考慮相機內參數的重構誤差極限值，所以需要利用式(11)進行重構精度仿真校驗并調整焦距設計值。

4 仿真校驗

為了測試空間目標三維重構觀測方案和相機參數設計方法的有效性，以假想的空間飛行器為目標，開展了觀測方案設計、相機參數選取和重構精度估計校驗。

假想的空間飛行器為立方星，如圖5所示，三維尺寸為1.6 m×1.6 m×1.6 m，期望重建精度1 cm。

圖5 空間目標三維模型Fig.5 3D model of space target

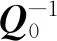
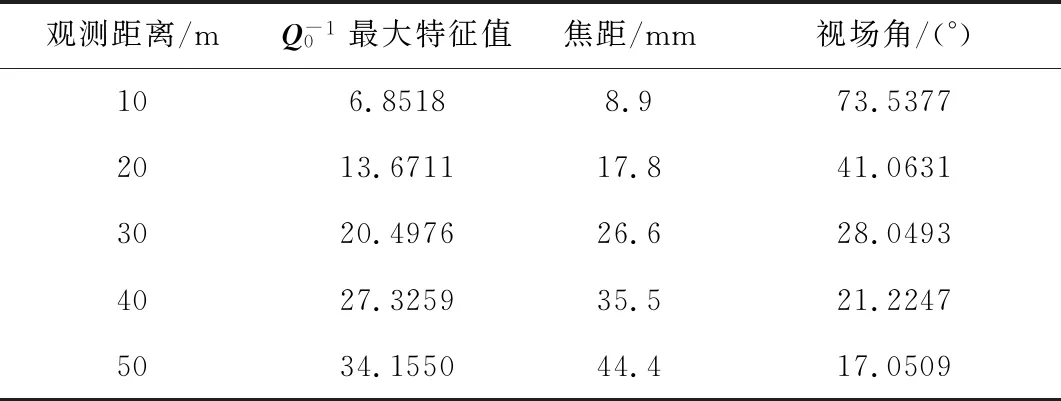
表3 不同觀測距離對應的焦距和視場角Table 3 Focal length and FOV of different distance

根據表3的給出的結果，觀測距離為30 m時，焦距26.6 mm可以保證重構誤差下限為1 cm。

接著，利用文獻[24]給出的CND方法對上述情形進行仿真，以比較兩種方法獲得的重構誤差極限。CND算法中相機參數設定為：焦距26.6 mm，像素尺寸13 μm。對目標3次成像在30°的繞飛弧段內完成，且兩次拍照至少間隔1°。為了減小遺傳算法搜索空間，限定相機光軸始終指向目標中心。適應度函數值為式(11)計算的重構誤差方差陣最大特征值。遺傳算法搜索過程由Matlab優化工具箱中的ga函數實現，其中遺傳算法交叉概率設定為0.7，變異概率0.005，適應度函數值隨進化次數變化曲線如圖6所示。

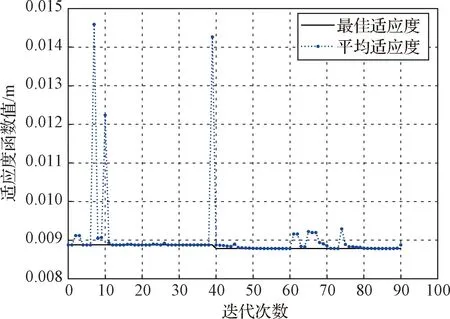
圖6 適應度函數值曲線Fig.6 The value of fitness function

經過90次進化，CND方法給出了重構誤差下限極值0.878 cm，最優拍照位置位于0°，1°和30°處。誤差極限與每15°采集一幀圖像取得的精度極限1 cm十分接近。進一步通過克拉瑪-羅不等式分析拍照位置與精度極限的關系發現，相同拍照弧段和相同拍照次數條件下，等間隔拍照策略的重構精度極限最差。因此本文采用等間隔拍照假設設計相機參數和觀測距離是保守的。

以上利用參數估計精度極限理論選取的相機焦距是理論上的最小值，還需要進行蒙特卡洛仿真校驗，并進一步調整其設計值。根據30 m觀測距離對應焦距26.6 mm，利用式(12)計算9個采樣點的重構誤差，仿真中設定特征跟蹤誤差標準差為0.25像素，并在觀測值上疊加高斯噪聲模擬測量結果。50次蒙特卡洛仿真結果為：采樣點重構誤差標準差最大值為3.47 cm，最小值為1.70 cm，平均值為2.27 cm，在CPU主頻3.2 GHz的計算平臺上共耗時304.5 s。

如果保持觀測距離不變，需要增加相機焦距以滿足重構精度要求。根據誤差標準差最大值3.47 cm，由式(10)和式(12)可估算焦距應增加至92.3 mm，對應視場角8.25°。再次進行蒙特卡洛仿真校驗，得到采樣點重構誤差標準差最大值為0.93 cm，最小值為0.51 cm，平均值為0.66 cm，已經滿足重構精度要求。

利用文獻[14]給出的重構誤差計算法，設定f=92.3 mm，像素尺寸13 μm，拍照間隔15°，采用與式(8)一致的尺度約束，計算采樣點重構誤差標準差最大值為0.78 cm，最小值為0.48 cm，平均值為0.58 cm，與本文給出的重構誤差計算方法結果十分接近，50次蒙特卡洛仿真計算時間為452.3 s。

最后利用三維重構軟件Visual SFM根據空間目標模擬圖像進行三維重構，考察重構三維點位置精度，以驗證觀測方案和相機參數的合理性。共使用拍攝間隔為15°的圖像3幀，特征提取與匹配采用SIFT算法，重構結果如圖8所示。

圖7 模擬目標圖像序列Fig.7 The sequence of target images

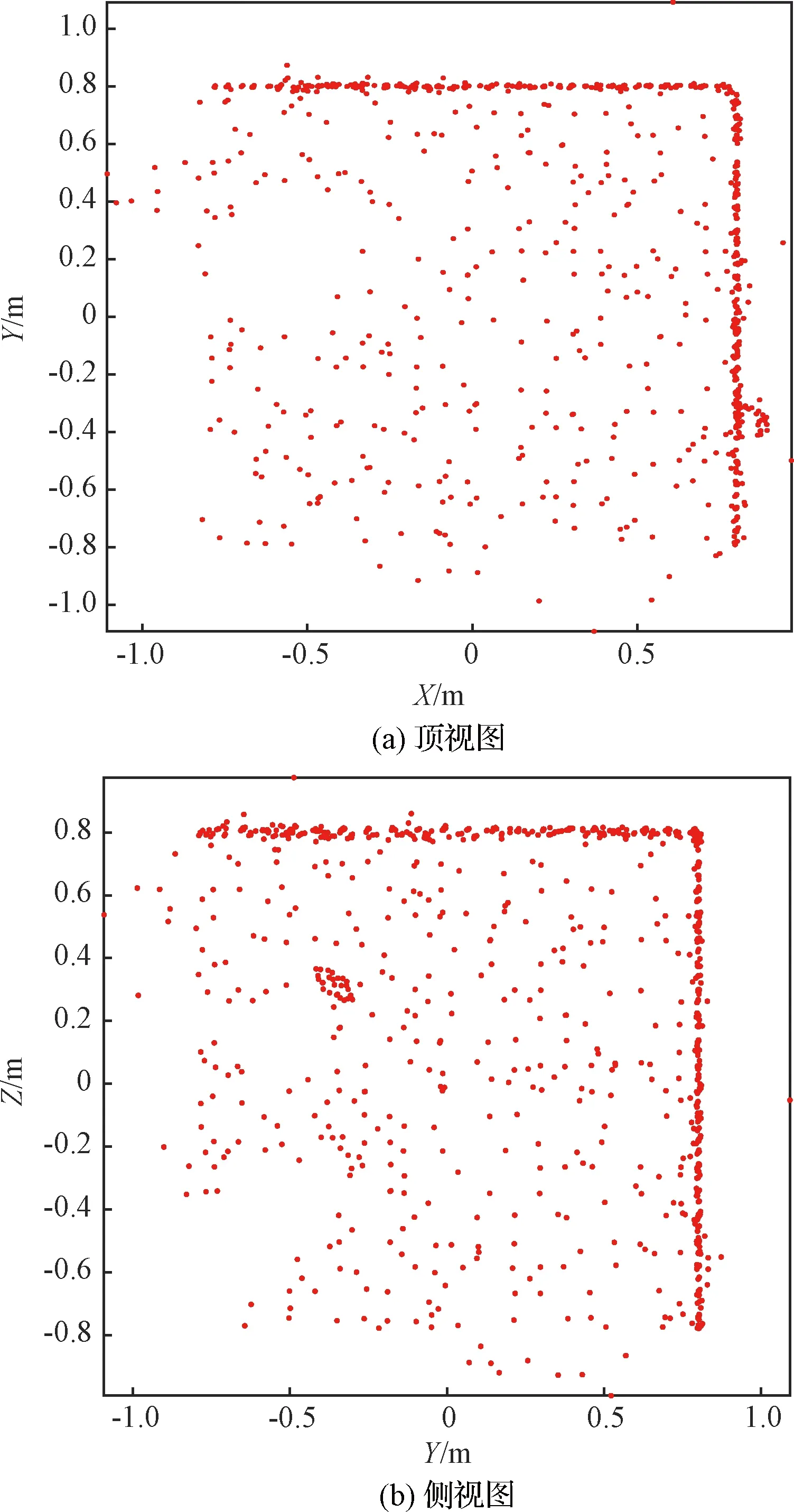
圖8 空間目標三維重構結果Fig.8 3D reconstruction results of space target

定義重構三維點與精確模型的最近距離(點到面)為重構誤差，在重構得到的1008個三維點中，重構誤差小于0.01 m的三維點數量802個。剔除41個與真實平面距離0.1 m以上的點后，重構誤差均值為-0.002 m，誤差標準差為0.0147 m，誤差直方圖如圖9所示。從圖9可以看出，重構誤差標準差與期望值0.01 m非常接近，說明本文提出的觀測距離拍照間隔與相機硬件參數選取方法是有效的。

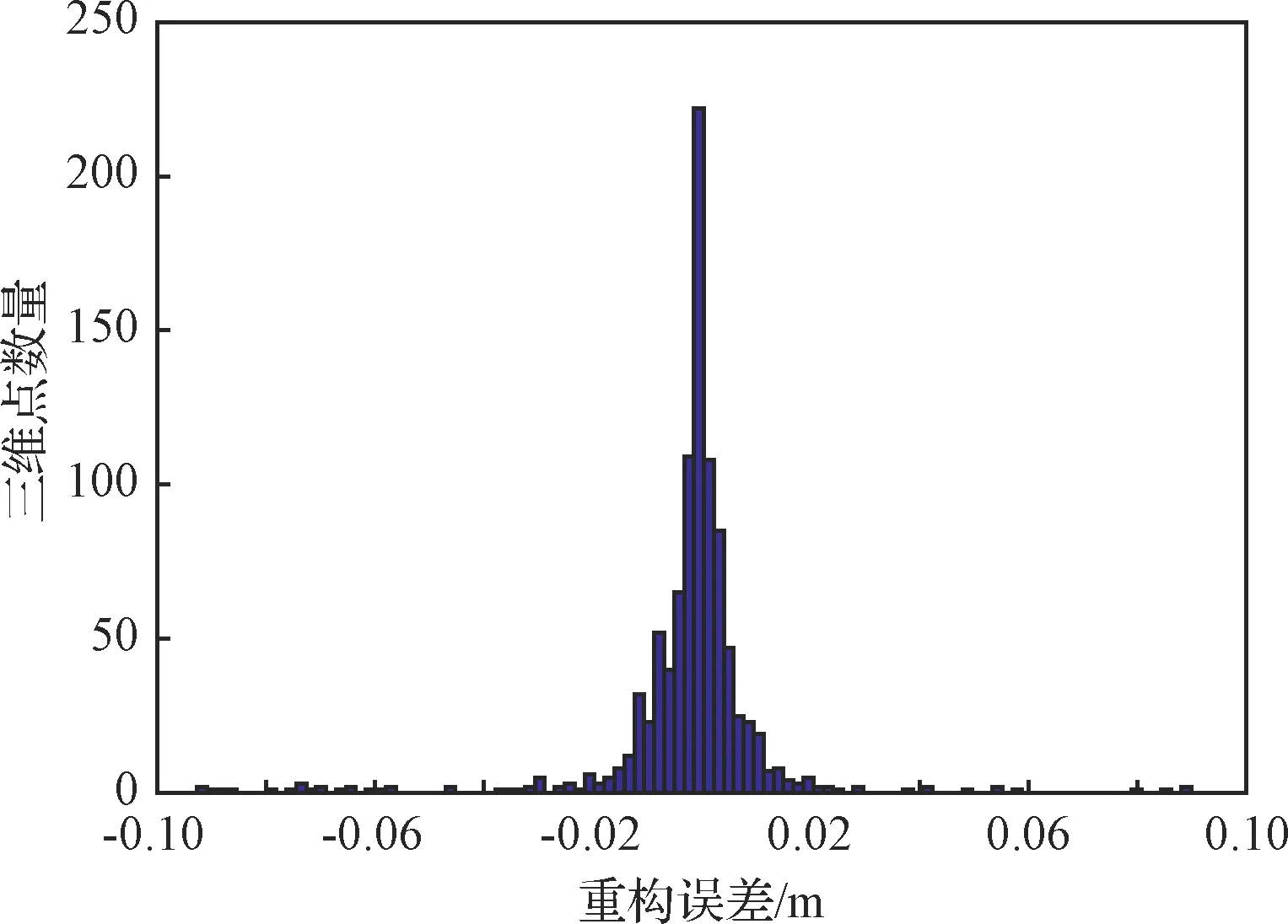
圖9 空間目標三維重構誤差直方圖Fig.9 Histogram of 3D reconstruction error

5 結 論

針對空間目標三維重構任務中的觀測方案設計和相機參數選取問題，在分析誤差傳播機理的基礎上，給出了重構精度估計方法；基于克拉瑪-羅不等式給出的參數估計精度極限，分析了觀測距離、拍照間隔和相機指向等參數與重構精度的關系；建立了以重構誤差為性能指標的觀測方案與相機參數選取方法。通過對模擬空間目標的重構誤差計算及參數設計仿真試驗可以看出，本文提出的觀測方案設計及相機參數選取方法是有效的，能夠滿足空間目標三維重構任務設計的需求。