品味奇妙投影
2019-09-05 07:55:46常文武
新高考·高二數學 2019年3期
常文武

在燈影下,我們的影子會嚴重扭曲.數學上看,光線在我們的“身”與“影”之間建立了一個“變換”.Sergio Aragones的漫畫就告訴我們這種變換多么不靠譜!
圖1的漫畫里,四人紙牌游戲鏖戰正酣,大贏家面前堆滿了贏來的錢,輸錢的另外三位面露笑容貌似祝賀贏家有好運,墻上的影子卻將三人的想法揭示無遺:等會兒拿刀追殺你,看你哪里逃?
的確,投影幾何的“變數”非常大:線段的中點投影后不再是影子的中點;圓甚至變成了拋物線或雙曲線!不過,再離奇的變換也有其不變的量——交比.
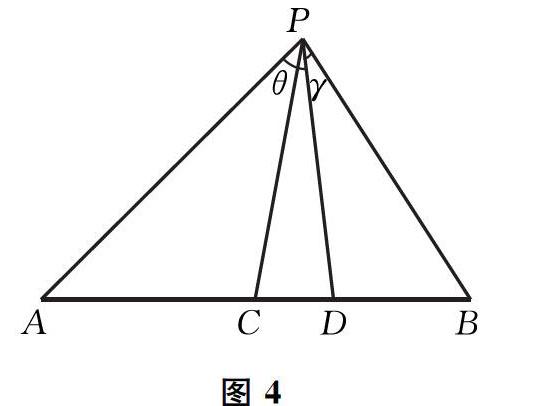
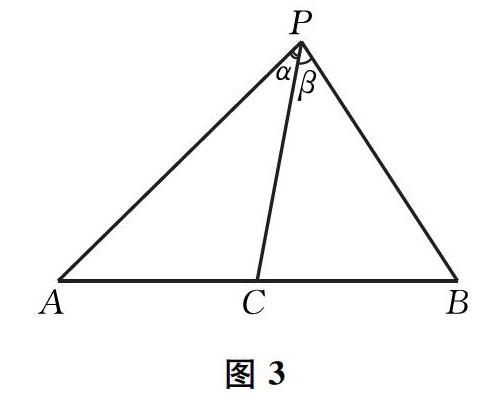
什么是交比?簡言之,交比就是兩個比的商,確切地說,當線段AB上有兩個分點:C和D(可以不管先后),它們分線段為兩個比AC:CB和AD:DB,那么這兩個比再作商AC:CB/AD:DB 或化簡為(AC×DB)/(AD×CB)就叫這四點的交比,記作(A,B;C,D).
也可以這么說,任何共線的4點可以看作3段線段a,b,c首尾相連的整體.第一段和后兩段的比是以:(b+c),第一、二段和第三段的比是(a+b):c,那么比之比(交比)就是ac/(b +c)(a+b).前文所斷言的就是在投影變換(數學上嚴格來說叫射影變換)下這個比是不變的(圖2).交比不變性是射影幾何學的核心概念,可以用初等平面幾何來證明這一性質.
漫畫家和數學家分別看到了影子的兩重性,影子對原物扭曲變化的同時,保留了內蘊的一個不變量——交比.
數學與藝術在人類文明的形成和發展過程中有著密切的聯系,它們都是構成人類文明不可或缺的一部分.談及數學與藝術,不得不提及將數學思想融于藝術設計的大師埃舍爾.他有些什么作品呢?讓我們一起來看一看.
猜你喜歡
中國寶玉石(2020年4期)2020-09-23 07:45:56
中國寶玉石(2020年4期)2020-09-23 07:45:56
讀者·校園版(2018年13期)2018-06-19 06:20:12
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
Coco薇(2016年2期)2016-03-22 16:58:59
讀者(2016年7期)2016-03-11 12:14:36
人間(2015年17期)2015-12-30 03:40:57
爆笑show(2014年10期)2014-12-18 22:27:48
作文評點報·低幼版(2014年47期)2014-11-25 23:43:21

