晃動基座下正向-正向回溯初始對準方法

徐 祥，徐大誠

(1. 蘇州大學電子信息學院,蘇州 215100；2. 蘇州大學微納傳感技術研究中心,蘇州 215100)

0 引 言

捷聯慣性導航系統具有自主性高、隱蔽性好、數據更新率高等優點，成為艦船、車用、消費類電子等產品定姿、定速、定位的首選系統[1-4]。捷聯慣性導航系統在進入導航定位之前，通常需要進行初始對準過程，以實現初始姿態角的獲取。當前常用的初始對準過程可以分為“粗對準+精對準”模式以及非線性濾波的大方位失準角初始對準模型[5-8]。文獻[9]提出了一種七階正交容積卡爾曼濾波(Cubature quadrature kalman filter,CQKF)算法，實現了SINS大失準角初始對準。然而，采用非線性濾波方法進行大失準角條件下的初始對準時，會導致計算量大、濾波不穩定、收斂速度慢等問題，使得其在工程應用中受到限制[10]。因此，大量研究均圍繞“粗對準+精對準”模式展開。

傳統“粗對準+精對準”采用兩個獨立的過程進行，即粗對準過程主要完成未知姿態角的粗估計[11-12]。文獻[2]提出了一種靜基座上自對準方法，文獻[7]實現了晃動基座上的粗對準過程。但這些方法都只是討論了不同狀態下的粗對準，無法實現姿態誤差的最小化。因此，需要通過粗對準過程，建立小角度誤差的導航系線性誤差模型，再利用Kalman濾波實現姿態角的進一步估計，從而完成初始對準過程[13-14]。

近年來，隨著計算機技術的不斷進步，其存儲容量和計算速度都得到了較快的發展，這也為基于回溯原理的快速初始對準奠定了基礎[15-19]。但這些方法都只是在粗對準或精對準中分別進行回溯，沒有充分將兩者進行融合，使得存儲過程冗余。另外，由于計算機在讀取存儲數據時，通常采用正向數據流形式，這使得傳統正逆向回溯過程在實時算法設計時較為復雜。而且，正逆向導航需要存儲所有時刻的慣性傳感器數據，這導致對存儲空間和計算速度要求較高，不利于快速對準的實現。基于傳統正逆向導航回溯初始對準方法存在的問題，本文將在導航慣性系粗對準的基礎上，提出一種基于導航慣性系誤差模型的精對準方法，并利用時不變姿態誤差估計方法，設計正向-正向回溯初始對準，解決傳統回溯對準方法設計復雜度高、數據存儲量大、計算效率低的問題，實現快速初始對準目標。

1 常用坐標系定義

為方便后續工作，基于正向-正向回溯原理的初始對準技術涉及到以下幾個坐標系，分別定義為[3]：

1) 地心慣性坐標系(i系)：選取初始對準起始時刻地球系作為初始地心慣性系，并且不隨地球運動而改變。

2) 導航坐標系(n系)：選取“東-北-天”方向為導航坐標系。

3) 導航慣性坐標系(n0系)：初始對準起始時刻導航坐標系，并且相對慣性系不變。

4) 載體坐標系(b系)：定義“右-前-上”為載體坐標系。

5) 載體慣性坐標系(b0系)：初始對準起始時刻載體坐標系，并且相對慣性系保持不變。

2 導航慣性系初始對準原理

為實現正向-正向回溯初始對準過程，本文將在n0系下建立系統誤差模型，并以此模型設計濾波算法，實現回溯對準。初始對準過程將分為粗對準和精對準兩部分。

2.1 導航慣性系粗對準

(1)

式中：

(2)

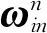
由慣導比力方程可知：

(3)

當載體處于晃動基座上時，可以假設載體無線速度運動，因此，式(3)可以采用矢量觀測器表示

(4)

式中：

(5)

假設陀螺儀量測和加速度計量測表示為：

(6)

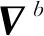
采用陀螺儀量測和加速度計量測構造矢量，可以得到

(7)

由式(2)可知：

(8)

由最優基姿態確定算法可知[16-17]：

(9)

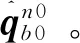
2.2 導航慣性系精對準

為了得到更高的初始對準精度，通常在粗對準之后需要進行精對準。傳統的初始對準方法中，精對準過程與粗對準過程通常互不相關，粗對準只為精對準提供一個粗略的姿態，精對準過程需要繼續采樣傳感器輸出,從而實現姿態誤差的估計。這一過程中沒有充分利用粗對準過程積累的有效數據，導致對準過程延長。同時，現代計算機的處理能力已能夠在一個傳感器采樣周期內進行多個濾波環節的運算，若需要等待傳感器采樣更新才能進行一次姿態誤差角估計更新，則大大浪費了計算機的處理速度，也延長了對準時間。因此，需要將粗對準與精對準進行融合，充分利用粗對準采集數據及計算機的處理能力，實現快速對準目的。

為實現這一過程，需要將傳統的時變姿態誤差角估計問題轉變為時不變姿態誤差角估計問題。因此，本文將對傳統的導航系誤差模型進行修改，設計導航慣性系誤差模型，從而實現時不變姿態誤差角估計。假設粗對準之后，方向余弦矩陣可以表示為

(10)

式中：

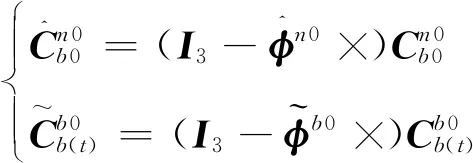
(11)

將式(11)代入式(10)可得

(12)

式(12)表示n0系下姿態誤差與方向余弦的關系。令

(13)

則有

(14)

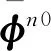
(15)

因此，n0系姿態誤差角微分方程可以表示為

(16)

從式(16)可以看出，姿態誤差角的變化只與陀螺儀量測誤差有關，考慮到對準過程較短，且陀螺儀量測誤差較小，可以近似認為姿態誤差角為時不變量。由坐標變換關系可知

(17)

由晃動基座條件可知，vn=0，因此式(17)可以表示為

(18)

將式(3)代入式(18)，并忽略n系速度項可得

(19)

因此，n0系速度誤差方程可以表示為

(20)

由式(16)和(20)可得n0系下系統誤差模型

(21)

(22)

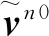
(23)

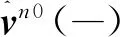
至此，基于n0系的初始對準模型建立完成。對上式(21)進行離散化，并采用Kalman濾波，即可實現時不變姿態誤差角φn 0的估計，從而實現精對準。

3 正向-正向回溯初始對準原理

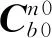
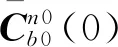
圖1 正向-正向回溯對準結構圖Fig.1 Structure diagram of forward-forward backtracking alignment method.

4 試驗與結果

4.1 仿真試驗

仿真硬件環境為Intel (R) Core(TM)T9600 CPU 2.80 GHz，4G RAM，Windows 7操作系統。利用Matlab profile功能對算法運行時間進行統計，檢驗算法的收斂速度。

表1 傳感器誤差設定Table 1 Sensor errors setting

仿真過程中，慣性傳感器誤差參數設定如表1所示。設定慣性傳感器數據輸出率為200 Hz。仿真過程模擬艦船系泊狀態下初始對準，設定晃動參數如表2所示。

表2 搖擺參數設定Table 2 Swinging parameters setting

在上述仿真條件下，采用最優基方法進行300 s粗對準，并對粗對準數據進行記錄，采用設定回溯過程為4次，得到對準誤差曲線圖如圖2～4所示。圖中點線表示第一次回溯結果、點畫線表示第二次回溯結果、虛線表示第三次回溯結果、實線表示第四次回溯結果。

粗對準結束時刻航向對準精度為0.5°，水平對準誤差為0.02°左右。當由粗對準進入回溯對準時，由于初始誤差協方差矩陣P0|0為經驗值，且通常設置為較大，導致在回溯起始階段出現較大的調節現象。但經過兩次回溯計算縱搖誤差角可以收斂到0.006°左右，橫搖誤差角可以收斂在0.004°以內，航向誤差角可以收斂在0.06°左右，達到了精對準的目標。同時，由于采用正向-正向回溯過程，不需要在回溯過程中進行大量IMU數據更新，使得算法可以在1.5 s內完成一次回溯計算，四次回溯過程計算時間為6 s。通過分析可以經過兩次回溯之后算法即可達到極限精度，因此總的對準時間為303 s，這大大提高了初始對準的收斂速度，達到快速對準的目的。

圖2 縱搖誤差Fig.2 Curves of the errors of pitch

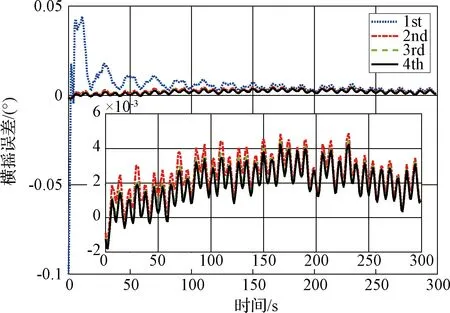
圖3 橫搖誤差Fig.3 Curves of the errors of roll

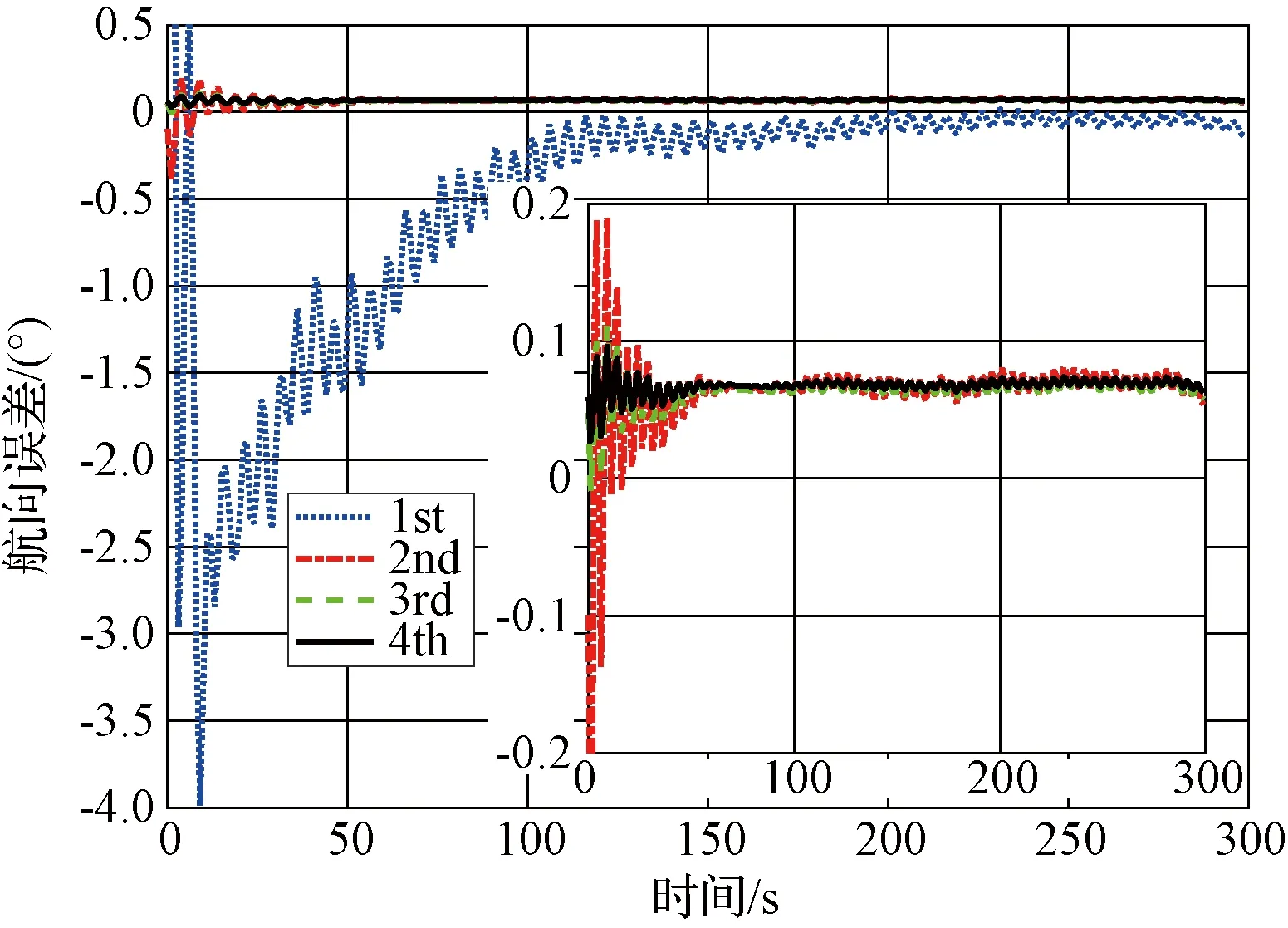
圖4 航向誤差Fig.4 Curves of the errors of yaw

4.2 轉臺試驗

在仿真試驗的基礎上，設計轉臺試驗，檢驗算法在實時系統上的對準性能。轉臺試驗實物圖如圖5所示。設定搖擺參數如表2所示，IMU數據更新頻率為200 Hz。對準過程中，先進行300 s粗對準，然后進行四次回溯對準，并以轉臺輸出為姿態基準，四次回溯對準過程誤差曲線如圖6、7和8所示。

從圖6和7中可以看出，水平姿態角在一次回溯之后即可達到穩定值，縱搖角誤差均值為-0.0007°，標準差為0.0156°，橫搖角誤差均值為0.0034°，標準差為0.0186°。航向角經過兩次回溯也收斂到穩定值，對準誤差均值為-0.057°，標準差為0.0077°。其中，一次回溯過程的計算時間為1.5 s，因此可以在303 s內完成初始對準過程，加速了對準的收斂速度，達到了快速對準的目的。

圖5 轉臺實物圖Fig.5 IMU and turntable

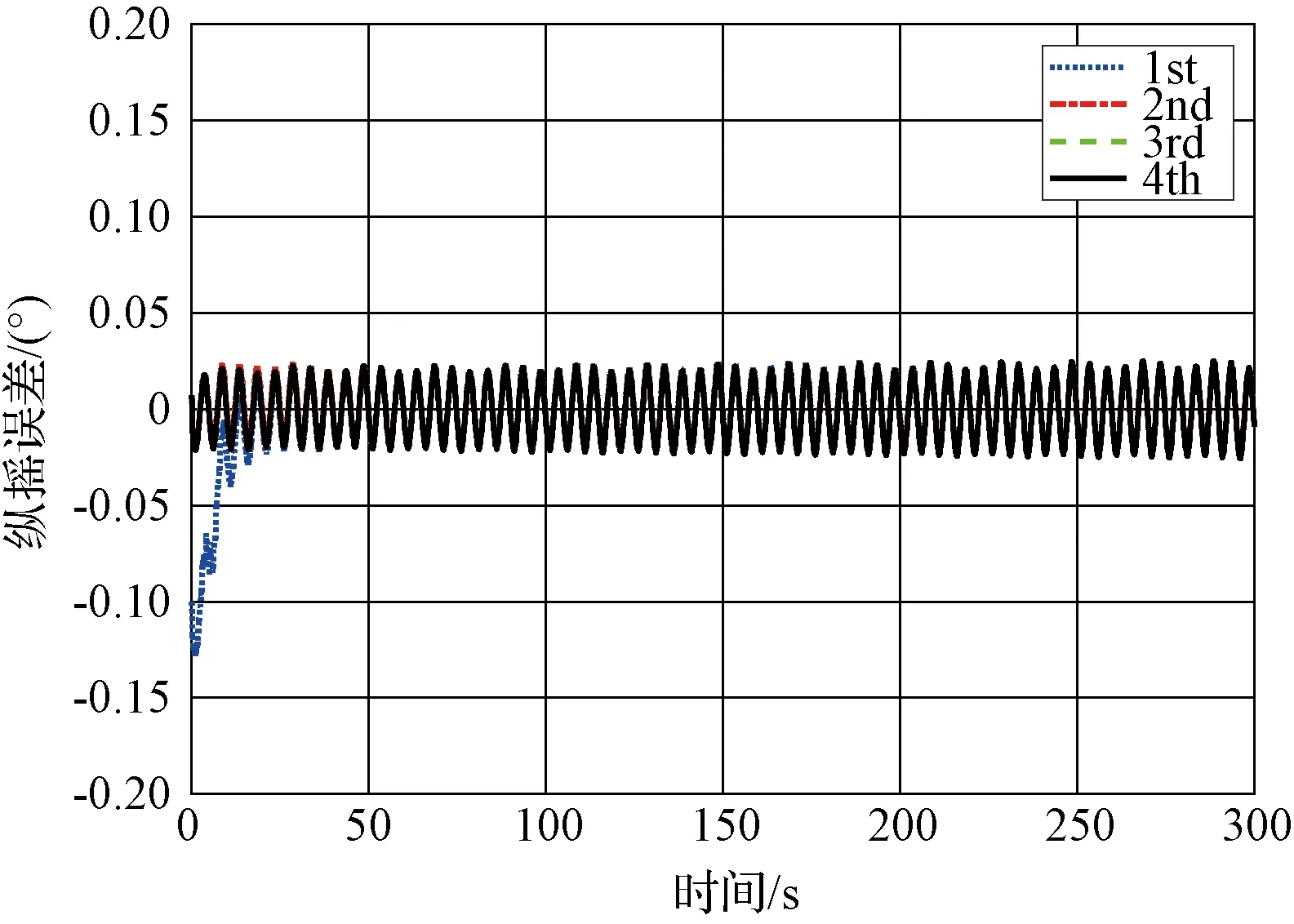
圖6 縱搖誤差Fig.6 Curves of the errors of pitch

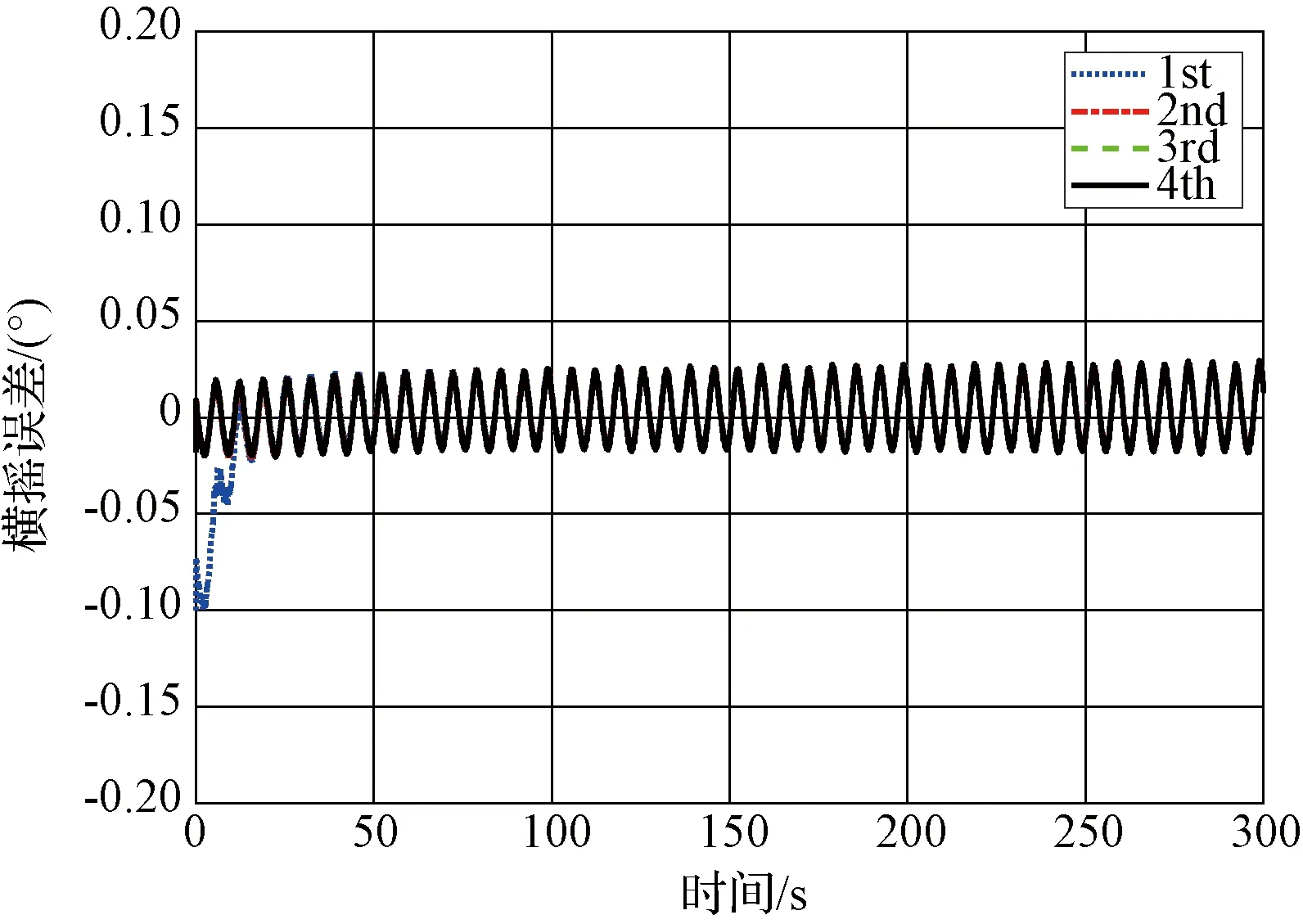
圖7 橫搖誤差Fig.7 Curves of the errors of roll

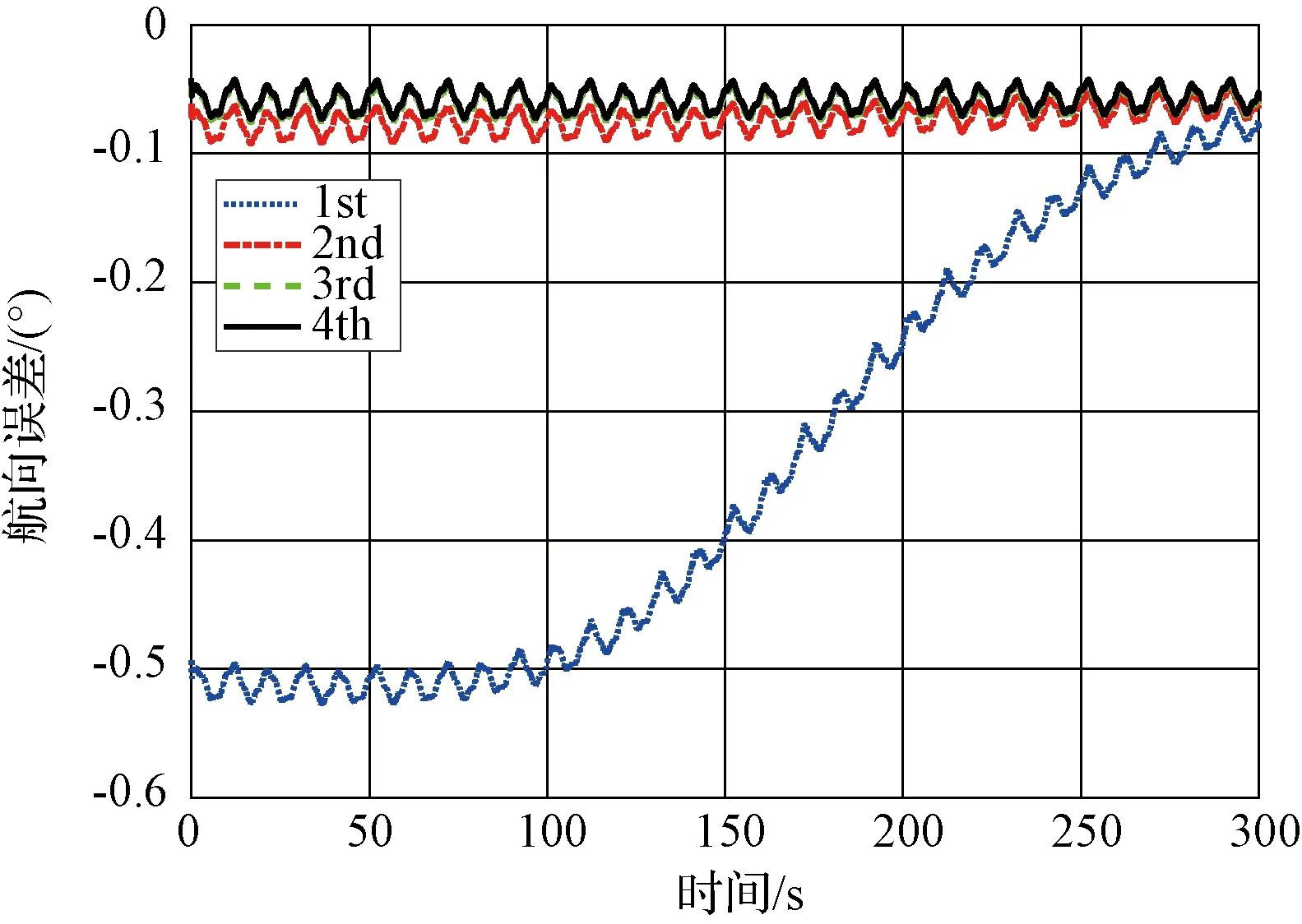
圖8 航向誤差Fig.8 Curves of the errors of yaw

在轉臺試驗中，由于轉臺數據是由慣導數據觸發的，這使得轉臺數據在輸出的時候相對于慣導數據存在延時現象，從而造成水平姿態誤差波動較大。

5 結 論

針對初始對準收斂速度與收斂精度的矛盾問題，本文設計了一種正向-正向回溯初始對準方法，利用慣性系初始對準基本原理，構造了基于n0系的系統誤差方程，實現了時變姿態估計到時不變姿態估計的轉變，為正向-正向過程奠定了基礎。通過設計仿真試驗與轉臺試驗，檢驗了正向-正向回溯對準在晃動基座上具有收斂速度快、對準精度高、計算效率高等優點，能夠解決初始對準收斂速度與收斂精度矛盾的問題。