運用線性規劃思想方法解決兩元變量取值范圍問題

☉江蘇省昆山中學 沈艷虹

《普通高中數學課程標準（2017版）》提出了培養學生數學學科核心素養的課程目標，即“在學習數學和應用數學的過程中，學生能發展數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析等數學學科核心素養.”這是對2003版實驗新課標提出的四基和四能目標的繼承、創新、提升和發展.作為一名高中數學教師，除了在平時的教學實踐中，把發展學生的數學學科核心素養貫穿于教學活動的全過程之外，更要分析研究并隨時把握新課標下高考命題的新方向，即“命題應依據學業質量標準和課程內容，注重對學生的數學學科核心素養的考查.”唯有此才能引領學生取得素養發展和高考成績的雙贏.經過對近幾年高考數學試卷的統計分析，筆者發現，簡單的線性規劃問題頻繁地出現，其命題形式靈活，考查范圍廣泛，內容覆蓋了方程、不等式、圖像、坐標平移等基礎知識.可以這樣說，圍繞簡單線性規劃來創設的問題情境已成為考查學生數學學科核心素養的載體，其中求線性目標函數在線性約束條件下的最值是常見題型，一般來說，學生只要把握線性規劃的基本思想與方法就能順利應答.但若題目在簡單線性規劃的基礎上，對約束條件和目標函數做一些非線性的變換，則對學生的數學學習質量水平提出了較高的要求，該類題目具有較高的區分度，能體現高考數學的選拔功能.下面結合教學實踐案例，就目標函數非線性和約束條件非線性下的兩元變量取值范圍的問題作初步的探討與反思.

一、類型1：目標函數非線性

在近年的高考數學卷中出現了求目標函數是非線性函數的取值范圍問題，此類題目情境多變，對考生的能力要求較高.常見的題型有以下幾種：

【案例1】截距問題

解析：（如圖1）令z=x2+y，則此式變形為y=-x2+z，z可看作是動拋物線y=-x2+z在y軸上的截距，當此拋物線與y=-x相切時，z最小.

故答案為72.

【案例2】比值問題

圖1

解析：（如圖2）是可行域內的點M（x，y）與原點O（0，0）連線的斜率，當直線OM過點取得最小值；當直線OM過點（1，6）時，取得最大值6.

圖2

【案例3】距離問題

當目標函數形如z=（x-a）2+（y-b）2時，可將z看作是動點P（x，y）與定點Q（a，b）距離的平方，這樣目標函數的最值就轉化為PQ距離的平方的最值.

圖3

解析：（如圖3）作出不等式組表示的平面區域.

設x2+y2=z，則z是以原點為圓心的圓的半徑的平方.

當圓x2+y2=z過點B（2，3）時取得最大值，

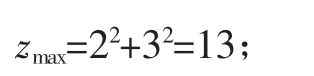
當圓x2+y2=z與直線AC：2x+y-2=0相切時取得最小值，從而z取得最小值.

設切點坐標為（x0，y0），則

【反思】從上述三個案例我們不難發現，當目標函數為非線性函數時，一般可以運用簡單線性規劃解決最值問題的思想方法去處理，所采用的方法和步驟也非常類似，其關鍵是先利用約束條件作出可行域，以確定目標函數對應的幾何意義；然后根據其幾何意義，利用數形結合的思想來求得其最值.這些問題主要考查學生的等價轉化思想、數形結合思想以及運動變化思想等等，不僅考查了學生的作圖、識圖能力，還對學生的觀察分析能力、聯想與想象能力以及邏輯推理能力提出了較高的要求.

二、類型2：約束條件非線性

【案例4】已知正實數a，b，c滿足c＞a，c＞b且=1，若a，b，c可構成某三角形的三邊長，求c的取值范圍.

錯誤解析：把條件c＞a，c＞b轉化為a+b＜2c.

這個解法運用了不等式中常用的“乘1法”，很多學生認為這是個很巧妙的解法，然而，很顯然在把條件轉化為a+b＜2c時，此為一個不等價的轉化，即c＞a，c＞b可以得到a+b＜2c，但反之不一定成立，所以求出來的c的范圍可能發生了變化，所以這是一個錯誤的解法.

正確解析：，這樣就能初步確定c的取值范圍，進而假設a，b，c可構成某三角形的三邊長，所以，還要滿足a+b＞c這個條件，這又該用怎樣的基本不等式才能解決問題呢？學生在運用不等式去解決該問題時遇到了困難.這時，如能結合題目中的已知條件，列出不等式組，則就可以運用線性規劃的思想與方法來求得最終的答案.

令c=y，b-9=x得

圖4

作出圖像（如圖4）

可得y即c的取值范圍是（16，+∞）.

【反思】當約束條件為非線性時，能結合所學的二次曲線、三次曲線等常見的函數圖像作出不等式所對應的平面區域是解題的關鍵，也是解題的難點.此類題目蘊含數學中基本的優化思想方法，能很好地考查學生的數學學科核心素養.除了考查學生的數學基礎知識、基本技能、基本思想和基本活動經驗外，還對學生的綜合分析能力、邏輯思維能力及解決實際問題能力提出較高的要求.所以在日常教學實踐中，教師要聯系學生的數學現實與生活實際，創設有效的教學問題情境，引導學生思維，利用信息技術呈現直觀圖像，以激發學生的學習興趣，在夯實學生四基與提升學生四能的過程中，發展學生的數學學科核心素養.

綜上案例分析，我們不難發現，線性規劃思想能夠很好的解決這類取值范圍問題，前提是題設為兩元不等式組，并能夠作出相應的可行域，再從中提煉出目標函數的幾何意義，然后利用數形結合思想，從而解決了基本不等式不能解決的最值問題.