基于核心素養的高中數學史教學實踐探究
☉重慶市永川北山中學校 黃基云
張國定的碩士學位論文《數學史融入數學教學的實踐研究》中鑒定了數學史的內容包括數學概念、數學定理與方法、數學家、數學美學、數學名題、數學游戲、數學名著等七個部分,高中數學是圍繞高考這個目標進行學習的,故把數學游戲的內容提升為高考數學研究,數學高考史是中國數學發展史的一個重要組成部分.《普通高中數學課程標準(2017年版)》提出高中數學的學習應掌握數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析這六大核心素養,高中數學史的學習也是圍繞六大核心素養全面展開的,下面將立足于數學核心素養,以探究高中數學史的教學實踐.
一、在數學概念教學中感知數學核心素養
數學概念的學習是高中數學的重要內容,很多學生對數學知識似懂非懂以及數學概念挖掘得不夠透徹,有些概念的引入是為了解決新的數學問題,例如對數函數的引入是為了解決指數方程解的問題,而有些概念的引入是知識體系的來源,例如橢圓概念形成的過程就是橢圓的定義,這些數學概念的教學既對學生的數學核心素養有一定的要求,又可以進一步提升學生的數學核心素養的深度,下面以橢圓概念作為教學實踐研究.
(一)教學引入
教師:同學們,讓我們一起復習一下初中學習的圓的定義.
學生:平面內到一個定點的距離等于定長的點的軌跡是圓.
教師:很好,讓我們一起思考一下,如果把一定點變為兩定點,到兩定點的距離之和等于定長的點的軌跡是什么?
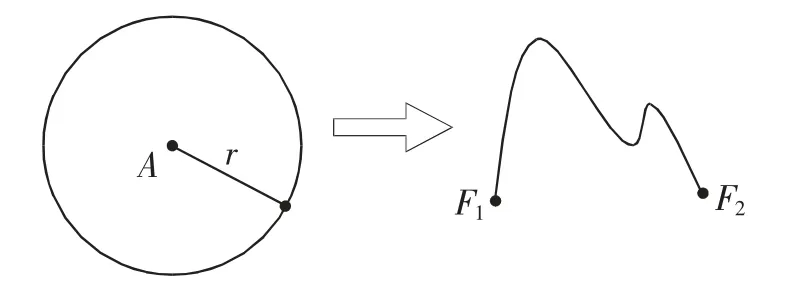
圖1
(二)實驗探究
教師:同學們,想知道到兩定點的距離之和等于定長的點的軌跡是什么嗎?讓我們一起來做個實驗求證一下,(1)取一條定長的細繩;(2)把它的兩端都固定在圖板的兩定點處,此時繩子的長度大于兩定點的距離;(3)套上鉛筆,拉緊繩子,移動筆尖,觀察筆尖的軌跡是什么?(教師拿出自制的簡易教學道具,請同學上臺實驗,隨著學生慢慢移動筆尖,逐次畫出一個橢圓)

圖2
學生:移動筆尖,得到的軌跡是一個橢圓.
教學:注意觀察此時的細繩的長度與兩條線段|PF1|、|PF2|之間有什么關系?
學生:細繩的長度=|PF1|+|PF2|.
教師:即到兩定點的距離之和等于定長的點的軌跡有可能是一個橢圓對不對?那一定是一個橢圓嗎?再觀察一下上述實驗,思考細繩的長度與兩定點之間的距離|F1F2|之間的大小關系?
學生:細繩的長度大于|F1F2|.
教師:也就是說細繩的長度大于兩點間的距離時,到兩定點的距離之和等于定長的點的軌跡是橢圓,那細繩的長度如果等于兩定點之間的距離|F1F2|,得到的軌跡還是橢圓嗎?讓我們再用實驗驗證一下(教師拿出一個細繩的長度等于兩定點的距離的道具,請同學上臺進行實驗,隨著筆尖的移動,學生畫出一條線段)
學生:當細繩的長度等于兩定點之間的距離|F1F2|時,得到的軌跡是一條線段.

圖3
教師:所以到兩定點的距離之和等于定長的點的軌跡是橢圓是有條件的,讓我們一起來總結一下有哪些條件?
學生:定長的距離大于兩定點之間的距離|F1F2|時才能形成橢圓.
教師:但是不要忘記開始的條件,故形成橢圓的條件有:①有兩個定點,記為F1、F2,兩定點間的距離用2c表示,即|F1F2|=2c,②有一個定長,記為2a,即2a=|PF1|+|PF2|,③最重要的是定長的長度要大于兩定點間的距離,即2a>2c.
教師:讓我們一起看課本上對橢圓所下的定義,是否就是我們實驗探究得到的形成橢圓的條件?
……
上面這個教學實踐從復習引入出發,根據邏輯并大膽推理——到兩個定點的距離之和等于定長的點的軌跡是橢圓,再利用數學實驗模型對推理的內容進行一一探究,得到到兩個定點的距離之和等于定長的點的軌跡可能是橢圓,也可能是線段,利用數據分析整理出形成橢圓的三個條件,最后利用數學抽象對實驗所得到的點的軌跡總結并歸納出橢圓的定義,在這一教學實踐中,要求學生具備基礎的數學核心素養技能,這樣學生的數學核心素養能力才可以在這一系列的推理——實驗——抽象出概念的過程中得到提升.
二、在數學定理與數學方法的演繹中領悟數學核心素養
數學定理和數學方法是解決數學問題的重要手段之一,也是應用數學的思路保證,學生要達到知其然更要知其所以然的目的,就必須掌握數學定理和數學方法的演繹,在數學定理和數學方法的演繹過程中各個核心素養之間的融會貫通,更是助其數學素養得到進一步提高的關鍵.例如在立體幾何中的向量方法教學過程中,在學習直線的方向向量和平面的法向量概念之后,引導學生推導出利用向量方法解決線線角、線面角、面面角的數學方法,其具體演繹如下:
相關概念:①直線的方向向量:空間直線的方向用一個與該直線平行的非零向量來表示,該向量稱為這條直線的一個方向向量;②平面的法向量:直線l⊥α,取直線l的方向向量a,則向量a叫做平面α的法向量.

圖4
線線角——空間中異面直線所成的角,如圖4所示:
方法:找到這兩條直線的方向向量,則向量的夾角即為線線角或者線線角的補角.
線面角——空間中線和平面所成的角,如圖5、圖6:

圖5

圖6
通過作圖發現直線的方向向量與平面的法向量的夾角有上述兩種情況,
第一種情況為向量的夾角與線面角是互余的關系,所以有sinθ=|cos〈a,n〉|,
即線面角的正弦值=向量的夾角的余弦值的絕對值.
綜上可證得:線面角的正弦值=向量的夾角的余弦值的絕對值,即sinθ=|cos〈a,n〉|.
面面角——空間中兩個平面所成的角,如圖7所示:

圖7
方法:分別找到兩個平面的法向量n1,n2,則兩個法向量的夾角為兩個平面所成的角或者所成角的補角.
在上述教學過程中,教師要指導學生利用邏輯推理并推理出向量的夾角和線線角、線面角、面面角之間的數學關系,再指導學生利用數學抽象,從圖形中抽象出方法并進行總結,建立空間直角坐標系的模型來解決數學問題,然后對空間坐標系下點的坐標等數據進行詳細地分析,最后利用數學運算把式子和結果運算出來,這一過程的教學,不僅提高了學生數形結合的能力,而且學生各方面的素養都得到了加強.
三、在對數學家的研究中植入數學核心素養
我國數學發展歷程十分曲折,從古至今有很多數學家為了中國數學的發展付出了畢生的精力,所以對數學家的研究是數學史教學中不可或缺的一個重要組成部分,在教學過程中,可以給學生介紹人民的數學家——華羅庚,他自學成才的故事可以用來激勵害怕數學運算的孩子們,他的“蘇家駒之代數的五次方程式解法不能成立之理由”的論文可以用來激勵孩子們勇攀數學的高峰.還有很多數學家嘔心瀝血研究的數學史記,這都是數學史教學的重要內容,這些數學家的奮斗史可以激勵學生不畏數學困難,敢于一頭扎進數學的學習中,從而為學生的數學核心素養的提高發揮重要作用.
四、在數學名著閱讀中感受數學核心素養
高爾基說過,書籍是人類進步的階梯,數學發展的每一次飛躍,都離不開書籍的幫助,特別是高中學生要面對高考的壓力,要想幫助學生在高考的數學學科中考出理想的成績,則在教學過程和日常生活中時刻滲透數學名著的重要性,介紹給學生一些數學名著,讓其在學累之時讀一讀,助其感受數學大師們的數學素養風采,感受數學的無窮魅力,讓學生在閱讀數學名著中愛上數學,在閱讀數學名著中感受數學核心素養.

