一種改進的輪廓曲線匹配算法
任家祥 張志剛 西安財經大學 信息學院
1 概述
圖像形狀匹配是計算機視覺的重要研究領域,目前輪廓曲線的匹配分為兩種,一是基于區域,二是基于特征點。文獻中將提取到的曲線進行最大公共子序列進行匹配,缺點是對于機器的性能要求較高,且匹配速度較慢。基于角點,采取粗、精兩種匹配方法,粗匹配基于歸一化角點距離矩陣,精匹配基于同心圓。因為需要進行同心圓計算,其匹配速率仍不高。將多邊形逼近算法與提取曲率相結合,提出一種速度較快的匹配方法,但是在進行多邊形匹配的時候,頂點的數目并不能確定,從而限制了匹配結果。
本文提出了一種輪廓曲線匹配算法:使用Canny 邊緣檢測算法提取出邊緣,使用Shi-Tomashi 算法對目標邊緣曲線角點進行提取。根據角點的位置點信息來建立出角點距離矩陣,并對其進行標準化處理。對處理過的角點距離矩陣視情況使用快匹配或慢匹配,分別適用于兩種不同的圖像匹配情況。
2 預處理
首先采用Canny 邊緣檢測算法得到細且明亮的輪廓曲線,再提取特征點,我們以角點作為圖像中重要的局部特征。本文采用的Shi-Tomasi 角點檢測算法基于灰度值,是對Harris 角點算法的改進。Shi-Tomasi 檢測算法流程如下:
(1)使用差分算子計算出x,y 方向的偏導數,計算出Ix^2,IxIy,Iy^2 四個元素值組成的2x2 的矩陣
(2)使用高斯濾波器處理(1)中的2x2 矩陣,得到結構張量矩陣M。
(3)由M 求得行列式的特征值r1 和r2,根據r1,r2 中的最小值來判定該像素點為強角點
(4)設定閾值Tc 和Td,對提取的特征點的數目和相鄰特征點的距離進行約束,這樣便于匹配點對數目的衡量和防止描述區域的重疊。
3 RPCP 輪廓曲線匹配算法
3.1 歸一化角點距離矩陣
在平移和旋轉之后,角點的位置會發生變化,為描述角點之間的相對位置,計算N個角點的歐式距離,從而建立一個N*N的二維矩陣,其計算公式為:
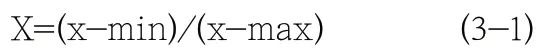
其中的max 和min 表示二維矩陣中所有元素的最大值和最小值。
3.2 快匹配
由上式得到兩個N*N 二維數組,如果將每個元素都與其余元素進行比較,那么總共需進行N^4 次比較操作。設兩個不同圖像的歸一化角點距離矩陣A 和B:

在快匹配算法中,將距離最大值點作為基準點,若該點到其它點的距離都能與另一點相匹配,則可以確定所有點之間的位置關系成功匹配。
算法流程如下:
(1)對矩陣的每一行按從小到大的順序進行快速排序。
(2)查找A、B 矩陣各自的最大值,記錄其所在的行,記錄結果為a1,a2,b1,b2。
(3)將a1,b1 進行匹配,若匹配結果不理想,則將a1,b2 進行匹配,記錄兩次匹配中的最優匹配結果。
(4)若匹配結果不理想,則將a1,a2 或b1,b2 換為次于當前距離的角點距離所在行。如果當前角點距離是前25%大,則進行(3),否則結束,將最優匹配結果輸出。
如果算法進行第(4)步多次,則快速匹配算法失效,說明這兩個矩陣之間極大值差距較大,則應采用慢匹配算法。
快匹配算法的時間復雜度在平均情況下是O(n).
3.3 慢匹配
慢匹配算法同樣基于歸一化角點距離矩陣,但慢匹配的目標不在于快速對兩個歸一化角點距離矩陣進行匹配,而在于最大限度得找出兩個矩陣之間的匹配程度。
在快匹配算法之中,優先匹配極大值角點距離,而慢匹配對所有角點距離一視同仁,原則上需要將每個點同其它所有點進行匹配。為減少匹配的次數,先進行排序,這樣匹配單位便由個上升為了行。其次,若該點與某一點的匹配程度理想,則應取消該點繼續匹配下去,這樣也能顯著降低匹配次數。算法流程如下:
設有兩條需要匹配曲線的歸一化角點距離矩陣A、B,A、B 為N*N 二維矩陣。
(1)將A,B 的每一行按從小到達的順序進行快速排序。
(2)將A 中的第n 行依次與B 中的每一行進行匹配,將匹配結果記錄下來,若匹配結果理想,則終止該行的匹配。
(3)n 值加一,重復(2)中的操作,記錄下每一行的最優匹配結果,直到所有行都匹配完畢。
(4)將每一行的最優匹配結果相加,得出最終匹配結果。
慢匹配算法的事件復雜度在平均情況下是O(n^3)
4 實驗與分析
實驗以某汽車品牌的標志為對象,共提取出了目標曲線20 個最優角點,建立歸一化角點距離矩陣之后,進行匹配。最終匹配程度達到95%。說明快匹配算法對于同一曲線的匹配有效。之后將一張紙不規則撕扯成兩半,并進行旋轉,同樣對圖像進行預處理并提取輪廓曲線。提取出20 個最優角點,將角點標記出來,如下圖:
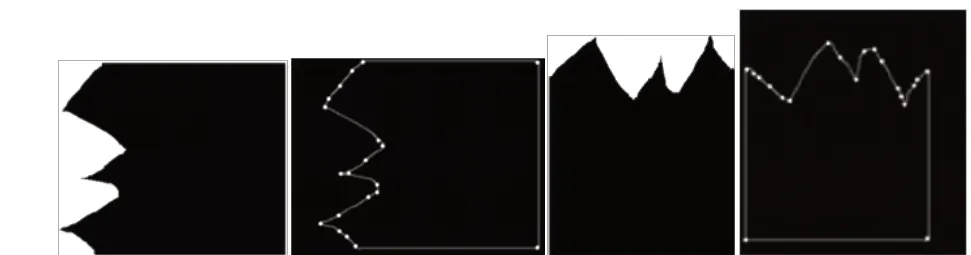
圖 4-1 原圖和角點提取圖
建立歸一化角點距離矩陣之后,使用快匹配算法,匹配程度為10%。說明快匹配算法對于不同曲線的匹配并不合適。則使用慢匹配算法,慢匹配算法的匹配程度達到75%,符合預期。說明慢匹配算法相較于快匹配更具有普適性。在對于差異較大的兩個矩陣進行匹配時采用慢匹配算法更為合適。
5 結論
本文提出了一種基于歸一化角點距離矩陣的輪廓曲線匹配算法,根據應用場景的不同,提出了快匹配算法和慢匹配算法。經過測試,快匹配算法對差異反應強烈,更適合于對曲線相似度要求高的領域。慢匹配算法能耐心地尋找出兩條輪廓曲線之間的最大相似程度,但時間復雜度較高。該算法的精度在一定程度上依賴于邊緣檢測算法和角點檢測算法。

