基于預警機引導信息的雷達最優搜索算法
(中國航空工業集團公司雷華電子技術研究所,江蘇無錫 214063)
0 引 言
先敵發現是對敵實施攻守行動的首要環節,也是信息化戰爭的關鍵階段之一。雷達作為戰場感知的主傳感器,實現雷達的快速搜索是先敵發現的必要條件之一;在現代中遠程空戰中,預警機的引導與指揮發揮著至關重要的作用,在預警機提供的先驗信息下,戰斗機能夠實現快速準確的發現目標和打擊目標;現代戰機所裝備的有源相控陣雷達具有波束捷變的特點,在空域快速搜索方面潛力巨大。因此,如何有效利用預警機的先驗信息來實現相控陣雷達的最優搜索是一個值得研究的方向。
關于相控陣雷達搜索問題,學術界已有較多的研究成果。文獻[1]對搜跟一體化情況下的搜索參數進行研究;文獻[2]對搜索駐留時間和幀周期進行研究;文獻[3-5]對搜索數據率進行了優化;文獻[6-9]各自針對不同的搜索工作參數,研究了優化算法。
現有的最優搜索模型主要考慮雷達時間資源的約束,較少從實際作戰需求的角度進行約束條件的分析。對于雷達探測威力區內已有目標存在的情況,空域的初始搜索順序優化要比搜索數據率的優化更為重要,然而,現有搜索模型較少考慮這方面問題;對于最優搜索過程中提出的多目標優化問題,現有文獻大都采用遺傳算法、粒子群算法等智能算法來進行模型的求解,雖然,這些算法能夠獲得有效解,但是,搜索速度較慢,相比于在實際作戰過程中需要實時在線優化搜索參數的問題來說,上述算法更適用于離線優化問題,工程應用價值不高。
本文在現有研究的基礎上,從預警機引導戰斗機雷達搜索的角度出發,建立了一種更為全面、更符合實際作戰需求的雷達最優搜索模型,并提出了一種適用于實際工程應用的實時求解算法。
1 基于預警機引導信息的雷達搜索問題描述
在實際作戰過程中,預警機引導戰斗機到達作戰空域,為了不提前暴露,戰斗機會在預警機的指引下確認敵機進入己方探測威力區后再打開雷達進行小范圍搜索,在打開雷達后,也有可能會有新的目標進入雷達的探測威力區,此時,預警機同樣可以為戰斗機雷達提供新目標的大概方位以及數量。
在不考慮射頻隱身性能的前提下,根據雷達搜索任務需求[6],本文采用以下搜索優化準則:1)目標累積發現概率最大準則;2)目標平均發現時間最小準則。
針對預警機引導戰斗機雷達搜索過程,雷達的搜索目標可以分為以下兩類:1)打開雷達時,探測威力區內已存在的目標(現有目標);2)后續進入雷達探測威力區內的目標(后續目標),本文假設后續目標均從雷達扇形搜索區域的最大探測距離邊界進入。
2 最優搜索模型的建立
2.1 模型描述
根據預警機的引導信息將搜索的扇形空域劃分成如圖1所示的M×N個子空域,即M行、N列,其中,行以距離為單位進行劃分,列以角度(這里的角度具體指方位角)為單位進行劃分。圖1中空域Λij表示第j行、第i列子空域。
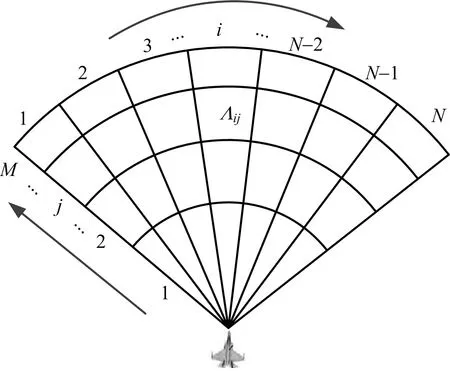
圖1 子空域劃分示意圖
2.2 優化目標分析
根據本文采用的兩個優化準則分別建立兩個性能評價函數,即目標累積發現概率和目標平均發現時間。
1) 目標累積發現概率
由文獻[5]可知,目標累積發現概率為
(1)
式中,pij為雷達在子空域Λij的平均探測概率,nij為更新時間Tg內子空域Λij的照射次數,ωij為各子空域的權重。
2) 目標平均發現時間
由文獻[5]可知,目標被發現的平均時間為
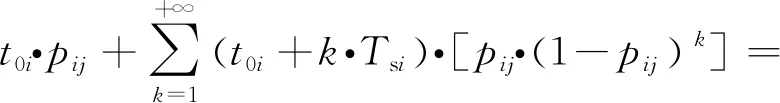
t0i+Tsi·(1/pij-1)
(2)
式中,Tsi為第i列子空域的搜索間隔,t0i為第i列子空域中目標從出現到緊接一幀搜索時刻的平均時間,k為目標被發現前的等待周期。
考慮到各子空域的權重ωij后,整個空域內目標被發現的平均時間為

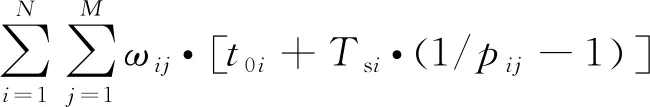
(3)
對于現有目標,第i列子空域中目標從出現到緊接一幀搜索時刻的平均時間為t0i即為該子空域的初始搜索時間,與子空域的初始搜索順序有關,假設第i列子空域的初始搜索順序為μi,則t0i的計算方法如下:
(4)
式中,Tk為搜索第k列子空域的時間。
對于后續目標,t0i則與目標出現的隨機過程有關,假設進入子空域的目標流服從泊松流,則t0i的計算方法如下[5]:
(5)
2.3 約束條件分析
1) 雷達搜索時間約束分析
約束條件為搜索時間占雷達總時間資源的比例per(0≤per≤1),因此,建立約束條件如下:
(6)
式中,Λ為所有列向子空域的集合,Λ=[1,2,…,N],Ti為搜索第i列子空域的時間,ni為更新時間Tg內第i列子空域的照射次數,ni=Tg/Tsi。
2) 照射次數ni約束分析
顯而易見,每個子空域在更新時間Tg內的照射次數ni需滿足以下約束條件:
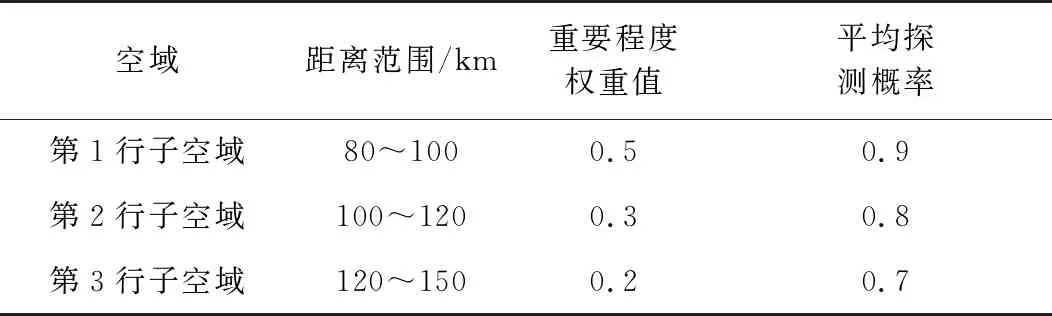
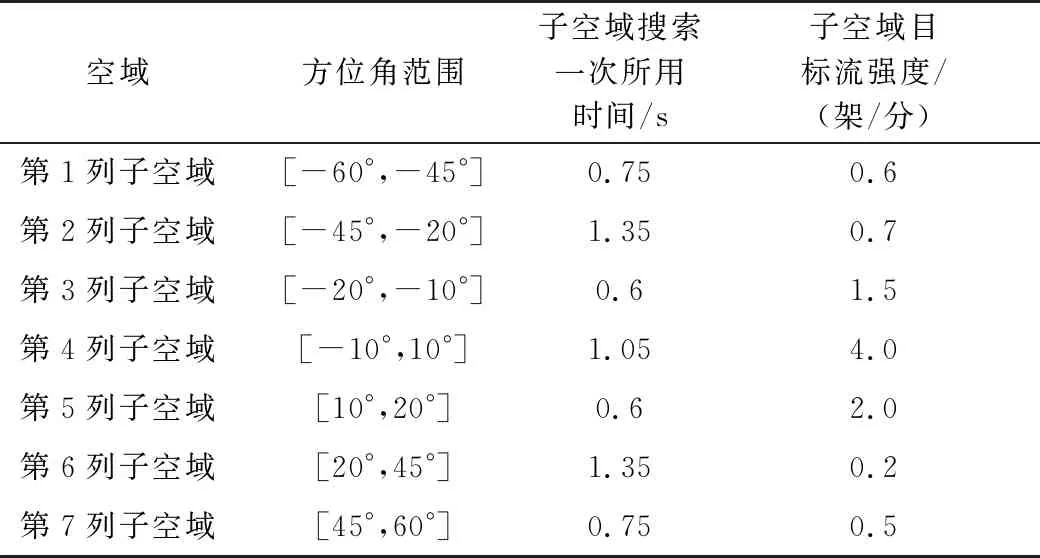
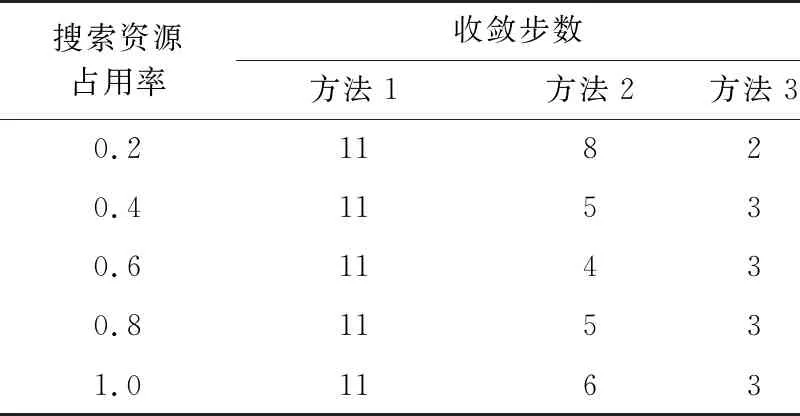
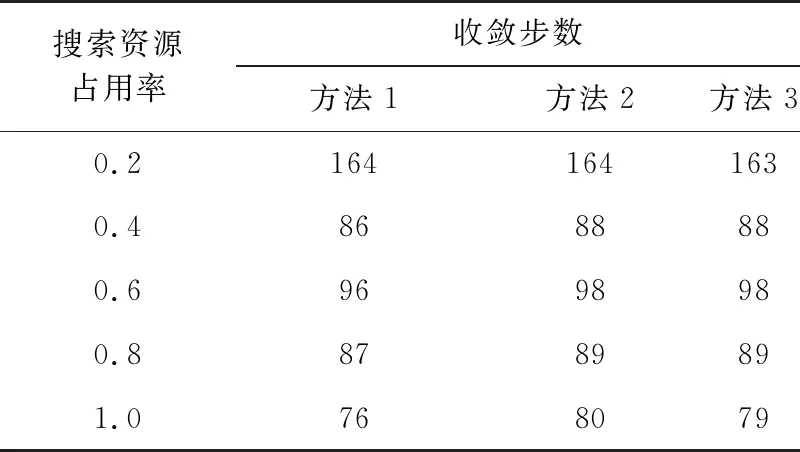
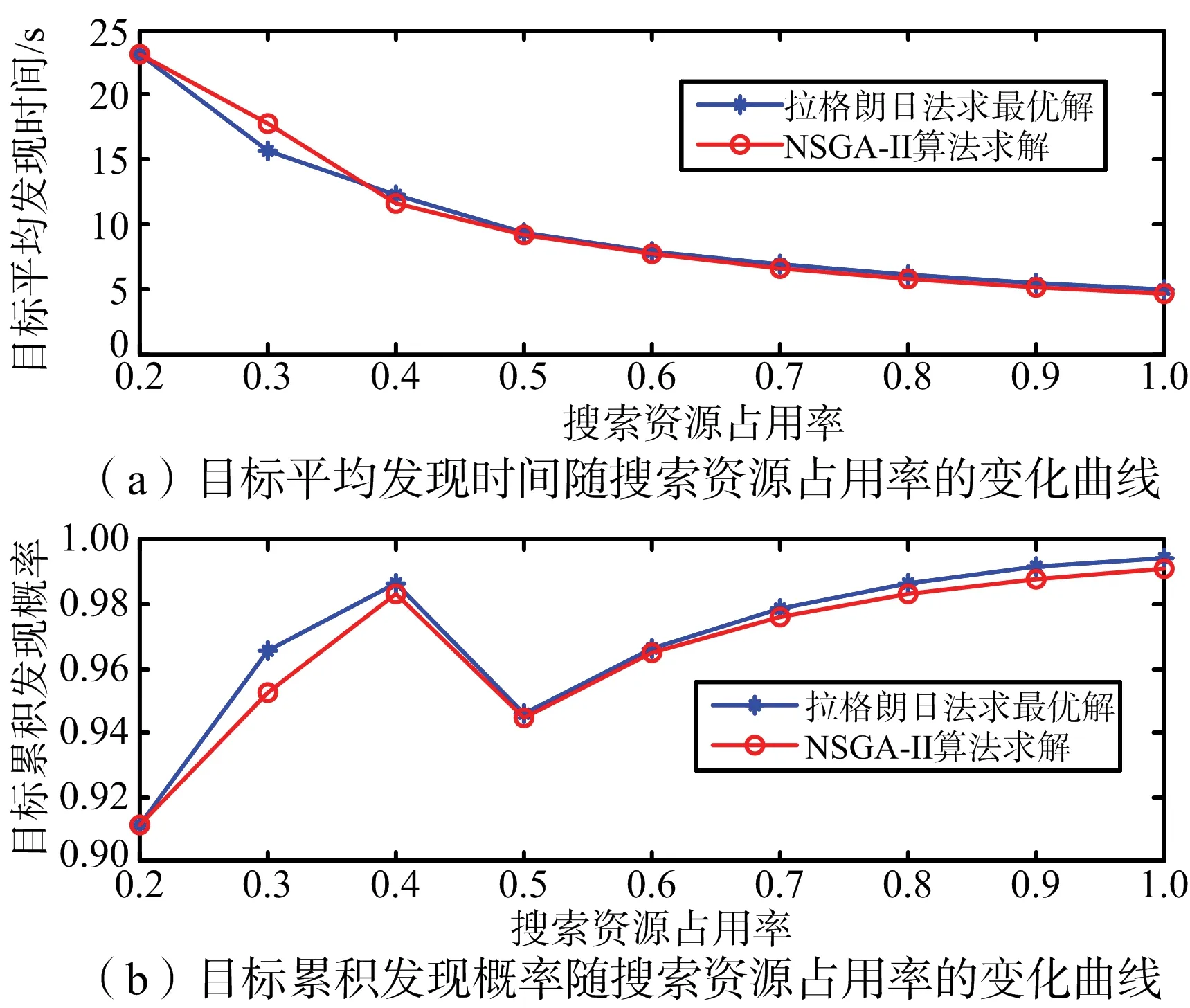
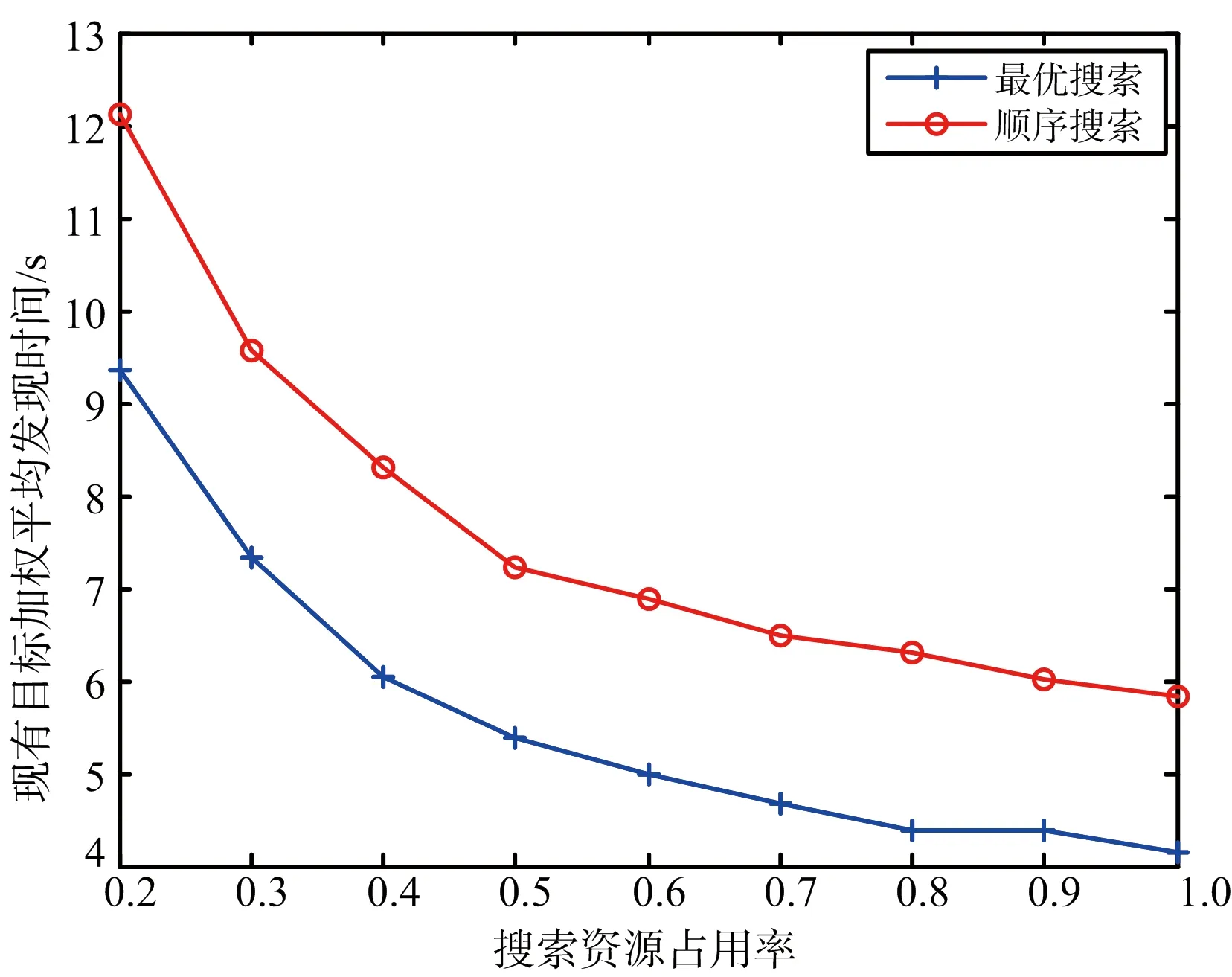
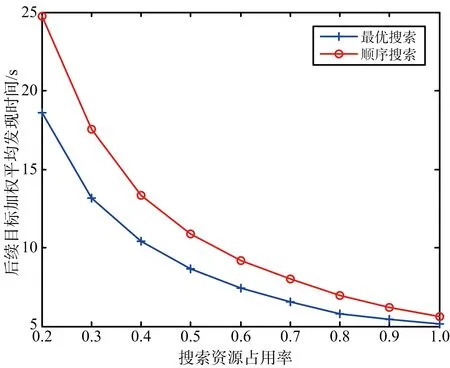
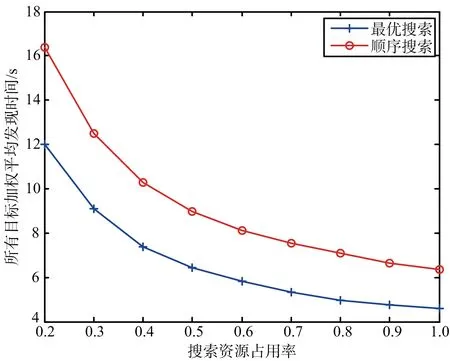
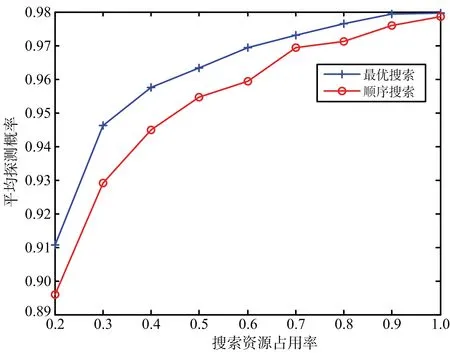
0 (7) 3) 目標最晚發現時間約束分析 在某些情況下,雷達在對目標進行搜索時對重點區域的目標會提出最晚發現時間的要求,因此,建立約束條件如下: (8) 第i列子空域現有目標的最晚發現時間為t0i。 為了建立第i列子空域后續目標最晚發現時間的數學模型,可以假設當目標累積發現概率超過一定閾值P0后一定會被檢測到。本文假設后續目標均從雷達扇形搜索區域的最大探測距離邊界進入,并且在搜索更新時間Tg內目標還未進入其他子空域,因此,第i列子空域后續目標在等待k個周期后被發現的概率為 Pki=piM·(1-piM)k (9) 式中,piM為第M行、第i列子空域的平均探測概率。 根據假設:Pki≥P0時目標一定會被檢測到,可計算出目標最晚在等待Ki個周期后一定會被發現,因此,第i列子空域后續目標最晚發現時間為 (10) 將式(10)代入式(8)可得 (11) (12) 式中,ε∈R+,且ε→0,即ε為趨于0的正實數。 根據2.2節和2.3節建立通用優化模型: (13) 對于現有目標來說,上述建立的通用優化模型的優化參數包括子空域的初始搜索時間T0以及子空域的搜索數據率Tsi;對于后續目標來說,優化參數只包括子空域的搜索數據率Tsi。對于兩類目標即對應的兩個搜索階段無法同時進行參數的優化。為了解決上述問題,本文采用一種兩步優化的方法。 1) 一步優化 在搜索的初始階段,對于雷達探測威力區內現有目標的發現時間,子空域的初始搜索時間遠比搜索數據率重要。一般在預警機的指引之下,雷達會在比較有把握的區域開機,即此時的探測概率較高。從數學角度分析,此時優化模型式(13)中的優化目標f1意義不大;另一方面,探測概率較高時,假設雷達可以一次探測到目標,此時,可以不用考慮數據率的影響。因此,可以將優化模型式(13)簡化為 (14) 由于上述優化目標只對子空域的初始搜索順序進行優化,因此,不存在約束條件。 2) 二步優化 在搜索的后續階段,基于目標流服從泊松流、后續目標均從雷達扇形搜索區域的最大探測距離邊界進入、在搜索更新時間Tg內目標還未進入其他子空域的假設,將式(5)代入式(13)后可得優化模型如下: (15) 式中,ωiM為第M行、第i列子空域的權重。 本文主要對二步優化的求解方法進行研究。 為了使得分析過程更加簡潔,將優化模型式(15)進行如下變形: (16) 式中,k1i=ωiM,k2i=ωiM·(1/piM-0.5)·Tg,piL=1-piM。 (17) 式中:h′1和h′2分別為優化函數h1和h2的歸一化參數;m1和m2分別為兩個優化目標的權值系數,m1+m2=1,可以通過調節m1和m2的大小來分配優化目標的重要程度。 1) 優化函數h1和h2在解空間上二階連續可微證明如下: 所以h1在解空間上二階連續可微。又因為 所以h2在解空間上二階連續可微。 2) 優化函數h1和h2在定義域上每一點的Hessian矩陣都是正定的證明如下: 優化函數h1的Hessian矩陣如下: (18) 式中,β1i=k1i·(lnp2i)2。 (19) 式中,piL∈(0,1],β1i>0。 同理,優化函數h2的Hessian矩陣如下: (20) 式中,β2i=2k2i。 (21) 下面對具體的求解過程進行分析。 3.2.1 拉格朗日乘數法求最優解 1) 拉格朗日函數 如式(22)所示的優化問題的拉格朗日函數為 L(φ,λ)=H+λ·G (22) 通過求解如式(23)所示的由N+1個方程構成的非線性方程組在定義域上的解即可得到等式約束條件下優化函數H的最優解。 (23) 2) 牛頓迭代求解 由于式(23)所示的非線性方程組比較復雜,無法直接求出解析解,因此,需要采用牛頓迭代法進行求解。迭代方程如式(24)所示: (24) 式中, F(φk,λk)= [F1(φk,λk)F2(φk,λk)…FN(φk,λk)]T 只有當式(23)所示的非線性方程組的雅克比矩陣是非奇異的,該方程組才可以用牛頓迭代法進行正常求解。方程組的雅克比矩陣如式(25)所示: (25) 經過計算可得F′(φ,λ)的行列式: (26) 在對ni進行約束的情況下,牛頓迭代有兩種結果: 1) 正常收斂,獲得迭代結果n*,判斷n*是否滿足定義域約束條件,如果滿足,則n*為式(17)的最優解,如果不滿足,則需進行障礙法計算。 2) 無法收斂,采用障礙法進行次優解的計算。 3.2.2 障礙法求次優解 1) 障礙法 采用障礙法求解,可以將式(17)所示的帶有2N個不等式約束的優化問題近似成如式(27)所示的等式約束問題[11]。 (27) 式中,Φ為對數障礙函數,t>0為確定近似精度的參數,在本文中Φ的具體表達式如式(28)所示: (28) 式(28)所示的優化問題與式(17)所示優化問題的最優解相差不超過2N/t,近似精度隨參數t的增加而不斷改進,然而,當參數t很大時,很難用牛頓迭代法極小化函數tH+Φ,這是因為Hessian矩陣在靠近可行集邊界時會劇烈變動,因此,可以通過求解一系列形如問題(27)的優化問題來規避上述困難,在這一系列問題中的參數t將逐漸增加,對于每個問題應用牛頓方法求解時可以用上個t對應問題的最優解作為初始點開始迭代,具體方法可參考文獻[11]。本文主要對確定某一個t值后式(27)的求解方法進行描述。 對數障礙函數Φ的Hessian矩陣如式(29)所示: (29) (30) 2) 拉格朗日函數 針對式(27)建立的拉格朗日函數如下: L(φ,λ)=(tH+Φ)+λ·G (31) 對應的最優解需滿足如下方程: (32) 3) 牛頓迭代求解 為了求解上述非線性方程組,同樣需要采用牛頓迭代法,此時,式(32)所對應的雅克比矩陣為 (33) 式中, 對應的行列式為 (34) 3.2.3 牛頓迭代初值的選取 由于牛頓迭代初值的選取對迭代算法的收斂性能有很大影響,本文分別采用以下3種方法確定迭代初值。 方法1:在解的范圍內任意選取一組數值作為初值; 方法2: 選取優化函數h1的最優解作為初值; 方法3: 選取優化函數h2的最優解作為初值。 仿真場景設置如下:雷達方位角掃描范圍為[-60°,60°],俯仰角掃描范圍為[-4.5°,4.5°],最大探測距離為150 km,本文只考慮80~150 km范圍內的空域;把搜索子空域按方位角和距離不同分為3×7個子空域,各子空域的重要程度和平均探測概率按目標離雷達的距離進行設置,具體參數如表1所示;各子空域的搜索時間和目標流強度按方位角進行設置,具體參數如表2所示;仿真時間為180 s。 表1 各行子空域參數表 表2 各列子空域參數表 4.2.1 不同牛頓迭代初值收斂速度對比分析 1) 拉格朗日法求最優解 在進行牛頓迭代收斂性能仿真時將殘差設置為10-6,不考慮目標最晚發現時間約束時,拉格朗日法求取的最優解大致都在定義域范圍內,此時,3種牛頓迭代初值選取方法的收斂速度仿真結果如表3所示。 表3 3種初值選取方法的收斂性能對比 表3給出了m1=0.5時3種初值選取方式下牛頓迭代收斂步數的對比結果,從表中可以看出,無論選取何種初值都能快速收斂,最大收斂步數不過11步,3種方法相比之下,選取優化函數h2的最優解作為初值時收斂速度最快,最大收斂步數不超過3步。 2) 障礙法求次優解 加入目標最晚發現時間約束時,部分情況下需要用到障礙法求取次優解。這里設置次優解與最優解的相差的精度不超過10-4,即2N/t<10-4,內迭代的殘差為10-6,假設第4列子空域為重點空域,式(11)右邊的式子滿足以下條件: (35) 此時,3種牛頓迭代初值選取方法的收斂速度仿真結果如表4所示,從表中可以看出在使用障礙法求解時,3種初值的選取方式迭代步數相差不大。 表4 3種初值選取方法的收斂性能對比 3) 初值選取 從上述分析可知,采用拉格朗日求解時,優化函數h2的最優解作為初值時收斂速度最快,采用障礙法求解時,3種初值條件的收斂速度相當,因此,選取優化函數h2的最優解作為拉格朗日結合障礙法的初值是最為合理的。 4.2.2 拉格朗日結合障礙法與遺傳算法求解性能對比分析 本文采用遺傳算法中的NSGA-Ⅱ算法與拉格朗日結合障礙法的求解性能進行對比研究。 圖2 拉格朗日法與NSGA-Ⅱ優化結果的對比 從優化性能分析:圖2給出了m1=0.7時拉格朗日法和NSGA-Ⅱ算法的優化結果,從圖中可以看出兩種方法計算的目標平均發現時間相差不大,拉格朗日法略微好一點,但是拉格朗日法的目標累積發現概率優化結果明顯比NSGA-Ⅱ算法好,從理論上講拉格朗日法可以獲得最優解,而NSGA-Ⅱ算法未必可以獲得最優解,因此,拉格朗日法的優化結果肯定不會比NSGA-Ⅱ算法差,但實際在計算過程中由于無法獲得拉格朗日函數的解析解,而是采用牛頓迭代進行計算,因此,采用拉格朗日獲得解也是近似最優解的一個次優解。圖3給出了m1=0.7時障礙法和NSGA-Ⅱ算法的優化結果對比圖,從圖中可以看出兩種方法的優化結果相當。基于上述分析,拉格朗日結合障礙法的優化結果要優于NSGA-Ⅱ算法。 圖3 障礙法與NSGA-Ⅱ優化結果的對比 從計算時間分析:本文采用MATLAB統計仿真時長,NSGA-Ⅱ算法平均一次計算時間約為53.8 s,拉格朗日結合障礙法平均一次計算時間約為3 ms。因此,采用拉格朗日結合障礙法的計算速度要遠遠小于NSGA-Ⅱ算法,滿足實時性的要求。 從上述分析可知,拉格朗日結合障礙法即凸優化的方法明顯比NSGA-Ⅱ算法有優勢,在實際工程中也具有更高的應用價值。 仿真場景如4.1節所述,為了與順序搜索進行對比分析,暫不考慮目標最晚發現時間的約束。按照上述仿真場景采用遺傳算法計算子空域初始搜索順序,采用拉格朗日結合障礙法計算各子空域的最優搜索數據率,并采用蒙特卡洛仿真對最優搜索算法的有效性進行驗證,在蒙特卡洛仿真過程中,現有目標根據各子空域的目標存在概率隨機生成,后續目標根據各子空域的目標流強度隨機產生。 圖4~圖7給出了不同搜索資源占用率下的蒙特卡洛仿真結果。圖4~圖6分別為現有目標、后續目標以及所有目標按照子空域重要程度進行加權的平均發現時間,從圖中可以看出,無論對于何種目標最優搜索的平均發現時間都要小于順序搜索。圖7給出了不同搜索資源占用率條件下,仿真時長內所有目標的發現概率對比圖,從圖中可以看出,最優搜索的發現概率要優于順序搜索,特別是在搜索資源占用率較小的時候,最優搜索的發現概率明顯優于順序搜索,當搜索資源占用率較大時,發現概率接近于飽和,二者差別并不明顯。 圖4 兩種搜索方式的現有目標加權平均發現時間對比 圖5 兩種搜索方式的后續目標加權平均發現時間對比 圖6 兩種搜索方式的所有目標加權平均發現時間對比 圖7 兩種搜索方式的發現概率對比 從上述分析可知,最優搜索的搜索性能要優于順序搜索,特別是在搜索資源占用率較小的情況下,最優搜索的優勢更為明顯。 本文主要針對基于預警機引導信息的雷達搜索問題進行分析,將雷達的搜索目標分為現有目標和后續目標兩類,并提出了通用的最優搜索模型,針對現有目標和后續目標的特點和差異,提出了兩步優化的策略;針對遺傳算法、粒子群算法等智能算法搜索速度慢,不適用于實際作戰的問題,將最優搜索多目標優化模型轉換成單目標凸優化問題,并提出拉格朗日結合障礙法實現搜索數據率的快速優化。通過數學推導驗證了該方法的合理性,并對牛頓迭代初值的選取方法進行研究。最后對本文提出的最優搜索模型和求解方法的合理性進行仿真驗證。 通過仿真結果可以看出:1)從優化性能和計算速度兩個方面來說,拉格朗日結合障礙法都優于遺傳算法;2)最優搜索算法的搜索性能優于順序搜索,尤其在搜索資源占用率較小的情況下,最優搜索的優勢更為明顯。
2.4 通用多目標優化模型建立
2.5 兩步優化模型建立
3 優化問題求解
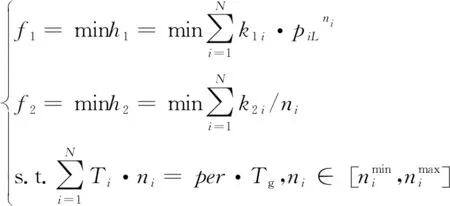
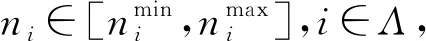
3.1 嚴格凸函數證明
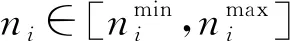
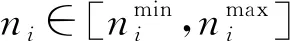
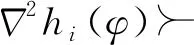
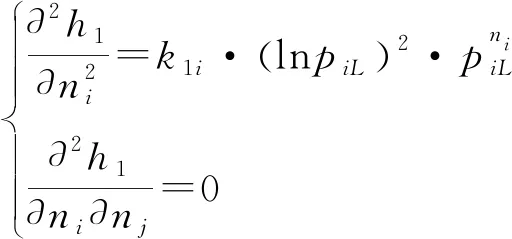
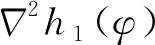
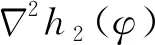
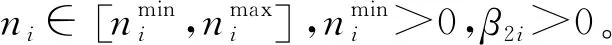
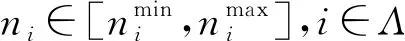
3.2 拉格朗日結合障礙法求解
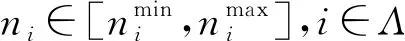
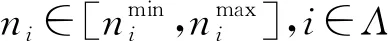
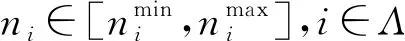
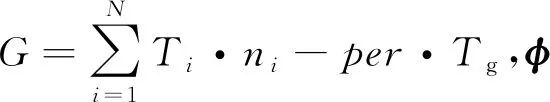
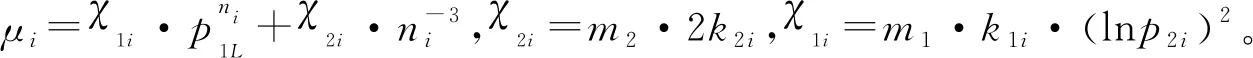
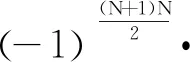
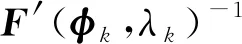
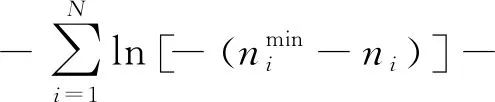
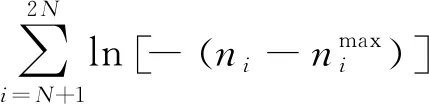
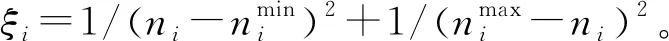
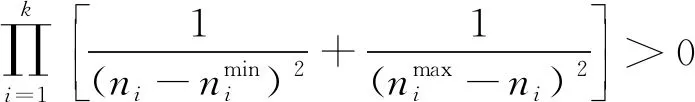
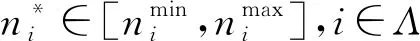
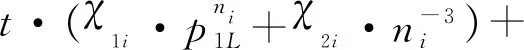
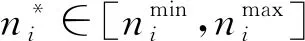
4 仿真分析
4.1 仿真場景設置
4.2 拉格朗日結合障礙法求解性能分析

4.3 最優搜索算法性能分析
5 結束語

