認知雷達二維自適應抗干擾捷變波形設計

(南京航空航天大學電子信息工程學院，江蘇南京 211106)

0 引 言

雷達干擾[1]是指一切破壞和擾亂雷達及相關設備正常工作的戰術和技術措施的統稱，按照干擾信號的作用機理可分為壓制性干擾和欺騙性干擾。其中，壓制性噪聲干擾是當前雷達干擾系統內一種重要干擾方式，主要以大功率的噪聲淹沒目標回波，大幅度降低雷達的工作性能，甚至使其無法正常工作。

認知雷達[2]通過自適應優化波形可以提高輸出信干噪比，提升雷達在干擾環境中的性能。對壓制干擾的抑制性可理解為發射信號與干擾協方差矩陣的二次型最小化，特征目標匹配波形設計問題可以歸結為二次約束下的二次型規劃(Quadratic Constrained Quadratic Programming，QCQP)問題。文獻[3]根據壓制干擾模型下的波形優化設計問題，提出了白化濾波器結構下基于干擾相關矩陣的波形設計方法。由于該方法獲得的優化波形往往具有很高的峰均比，不利于固態發射機發射功率的利用，且自相關性能較差。考慮到上述問題，文獻[4]將設計波形與典型波形間的相似度引入目標函數，提出了一種干擾環境下SWORD波形設計方法，能夠同時優化峰均比和自相關性能，提高干擾抑制能力。文獻[5]利用二次型規劃的迭代算法，設計了一種能夠同時設計恒模序列和干擾抑制濾波器的方法。文獻[6]以最小化不同距離單元的散射系數的均方誤差(Mean Square Error，MSE)為目標函數，在干擾譜方差矩陣內的子空間內，采用交替迭代法對目標函數進行優化求解，提高系統的信干噪比，達到抗干擾的效果。

但上述抑制壓制性干擾波形設計方法都是針對一維調制優化，即快時間維，并沒有充分利用雷達系統發射端的自由度。而二維調制優化能夠發揮雷達系統的自由度，提高接收端目標檢測性能。二維調制的維度一般可分為快時間域(又稱距離維、脈內調制)、慢時間域(又稱多普勒維、脈間調制)這兩個維度，由于通常調幅方式會降低發射機效率，因此調制維度一般限制在相位域。

本文針對壓制性干擾環境中認知雷達捷變波形設計，研究發射端二維調制優化準則和數學模型，并且提出降維策略，設計低復雜度的優化算法，在脈間采用動目標檢測處理，最終提出完整的捷變波形二維調制優化流程和方法，并仿真驗證該算法的可行性。

1 認知雷達二維自適應抗干擾捷變波形設計算法模型

認知雷達捷變波形波形設計中，二維調制模型如圖1所示。在一個相干處理間隔(Coherent Processing Interval，CPI)內，發射端發射N個脈沖，每個脈沖利用M個子脈沖編碼進行調制，且各個脈沖的調制都不相同。

圖1 二維調制模型

設一個發射雷達系統發射N個連續脈沖序列，表示如下：

(1)

式中，sn(t)為第n個發射脈沖的復包絡，Tr為脈沖重復周期(Pulse Repetition Interval, PRI)。假設脈沖sn(t)的持續時間T=Mtp，其中tp表示子脈沖持續時間，M表示sn(t)的子脈沖碼長。

(2)

式中，x(n,m),n=0,1,…,N-1,m=0,1,…,M-1是需設計的調制編碼序列。

(3)

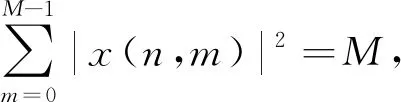
脈沖sn(t)的脈沖能量為

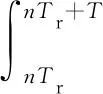
(4)

假設雷達環境中干擾信號為j(t)，J為干擾協方差矩陣，接收端的信號為

yn(t)=sn(t-τ)ej2πf(t-nTr)+j(t)

(5)

脈沖多普勒信號處理的第一步是對接收端的回波進行濾波處理，對于點目標的第n個脈沖，設接收端的濾波器為

(6)

那么濾波器的輸出為

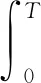
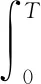
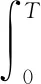
(7)

式中，τ和f分別為目標時間延遲和多普勒頻移。若所有多普勒移頻滿足-1/2Tr≤f≤1/2Tr，對于任意第n個脈沖，其持續時間足夠小，滿足|2πfT|<π/5，即T≤Tr/5，因此由動目標多普勒頻率引起的回波相位變化，可以忽略不計。并且，設時間點τ=ptp，p=-M,…,1,…,M，為子脈沖時間長度tp的整數倍。在τ=ptp時間處，由于Tr?tp，χn(τ,f)為

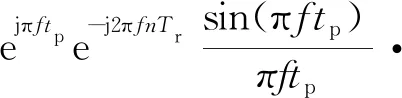
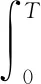
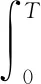
(8)

在脈沖多普勒雷達處理流程中，第二步是基于離散傅里葉變換處理相干脈沖序列。為了對一個特定延遲脈沖組進行相干處理，就必須在特定延遲處對前N個脈沖進行采樣。因此，匹配濾波結果可用一個2(M-1)×N的二維矩陣ξ(p,v)來構造，第一維表示時間延遲，第二維表示脈沖數目。對于一個特定的延遲，對匹配濾波結果的每一行進行N點逆離散傅里葉變換。并且頻率間隔v=q/NTr，其中q=0,1,…,N-1，為表示方便，化簡如下：

(9)

顯然，理想的模糊函數在原點處具有高的窄峰，在其他地方旁瓣和干擾信號為零。由于目標多普勒頻率f僅影響多普勒頻率軸上的高峰值位置，并且旁瓣能量及干擾信號被限制在所有相關的f，因此可以設置f=0并且定義脈沖串的距 離-多普勒模糊函數。

(10)

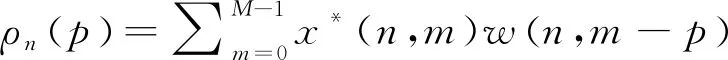
假設IΩ是距離-多普勒范圍內除零延時位置處(p=0)，包含(p,q)位置的子集，為抑制旁瓣和干擾信號，則需在IΩ范圍內最小化ξ(p,q)，可表示為

s.t.x(n,m)Hw(n,m)=1

(11)

|x(n,m)|=1

n=0,1,…,N-1,m=0,1,…,M-1

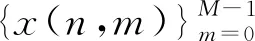
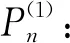
s.t.x(n,m)Hw(n,m)=1

(12)

|x(n,m)|=1

m=0,1,…,M-1

顯然式(12)最小化目標函數的物理意義為在理想狀態下，在p=0位置處，濾波器的輸出χn(ptp,f)有一個尖峰，其他位置在IΩ區域內，濾波器的輸出χn(ptp,f)接近于零，能夠達到抑制旁瓣及干擾的作用。

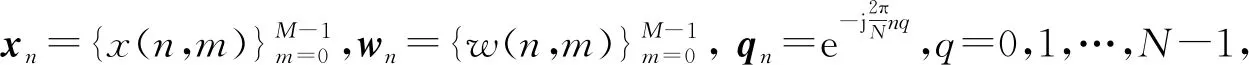
Qs為發射信號與濾波器的互相關矩陣，⊙為哈達瑪積。

(13)

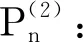
2 模型求解方法

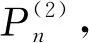
(15)

(16)

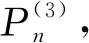
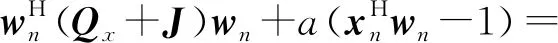
(17)

式中，a是Lagrange乘子，不為0的常數。

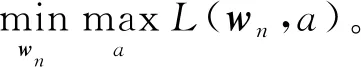
當式(18)成立時，L(wn,a)取得最小值。

(18)

則目標函數轉化為

(19)

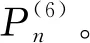
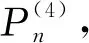
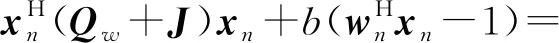
(20)

式中，b是Lagrange乘子，不為0的常數。

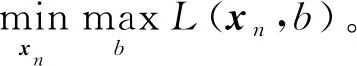
當式(21)成立時，L(xn,b)取得最小值。

(21)

則目標函數轉化為

(22)

利用線搜索法求得b，將b，wn的表達式代入式(21)可求得發射信號xn。認知雷達二維自適應抗干擾捷變波形設計模型算法求解過程如下：

Step 1：設參數脈沖個數為N，碼長為M，初始發射信號為隨機相位編碼信號，模恒為1，設定干擾信號為j(t)=[U0+Un(t)]exp[j2πf0t+φ0]，計算其協方差矩陣為J；

forn=0∶N-1

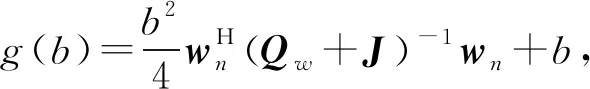
3) 對xn進行恒模處理，xn=ej(arg(xn))；

end

3 仿真實驗和性能分析

選取參數：發射信號s碼長N為200，旁瓣信號用平均旁瓣電平來表征旁瓣性能，在數學形式上表征為2范數平方的均值。接收端濾波器為w，干擾信號為Uj，其協方差為Rn。輸入信干比定義為在雷達發射端，發射信號與干擾信號平均功率之比，SIRin=10lg(E(s2)/E(Uj2))；輸出信干比定義為在雷達接收端，目標信號回波和干擾信號平均功率之比，SIRout=10lg((s*w)2/wHRnw)。干擾信號為壓制性噪聲調幅干擾信號，信號表達式為Uj=[U0+Un(t)]exp[j2πf0t+φ0]，射頻信號的幅度U0為0，中心頻率f0為35 MHz，初始相位φ0為0，調幅噪聲Un(t)是一個均值為0，方差為1，分布區間為[-U0,+∞]的廣義平穩隨機過程，φ0服從[0,2π]均勻分布。

圖2為噪聲調幅干擾信號功率譜分析。其中圖2(a)為調幅噪聲Un(t)功率譜，圖2(b)為已調波噪聲功率譜。從仿真結果可見噪聲調幅干擾功率集中在中心頻率f0=35 MHz，幅度為20 dB左右。

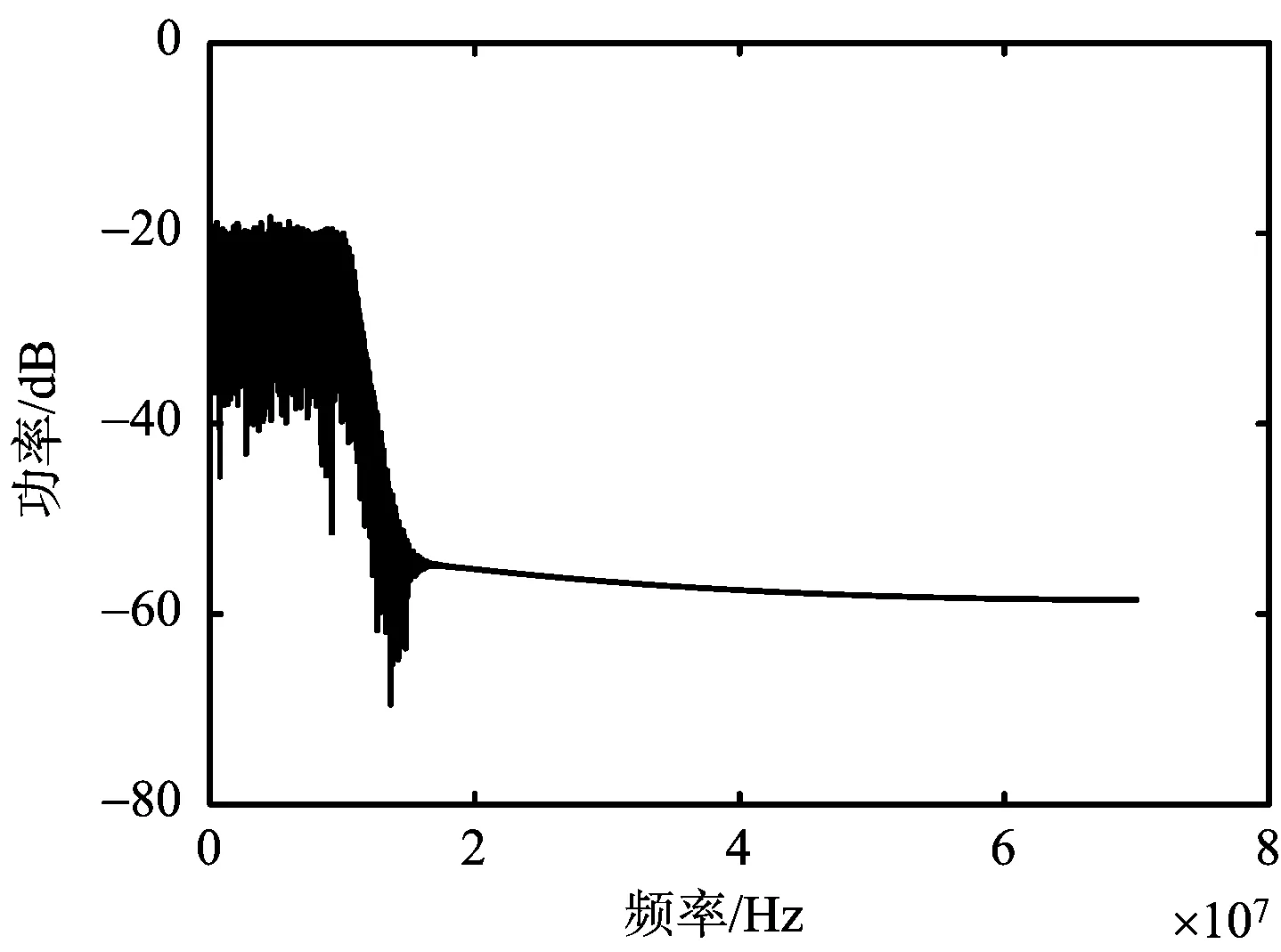
(a) 調制噪聲功率譜

(a) 優化前

(b) 優化后圖3 單脈沖干擾抑制的優化前后對比圖

圖4為二維自適應抗干擾優化模型的模糊函數圖。其中顏色條表示信號強度，單位為dB。由圖4可知，當輸入信干比較大時，目標信號被淹沒在壓制干擾中，無法被檢測出。通過優化設計二維發射信號及接收端濾波器，能有效抑制干擾信號，提高目標檢測性能。

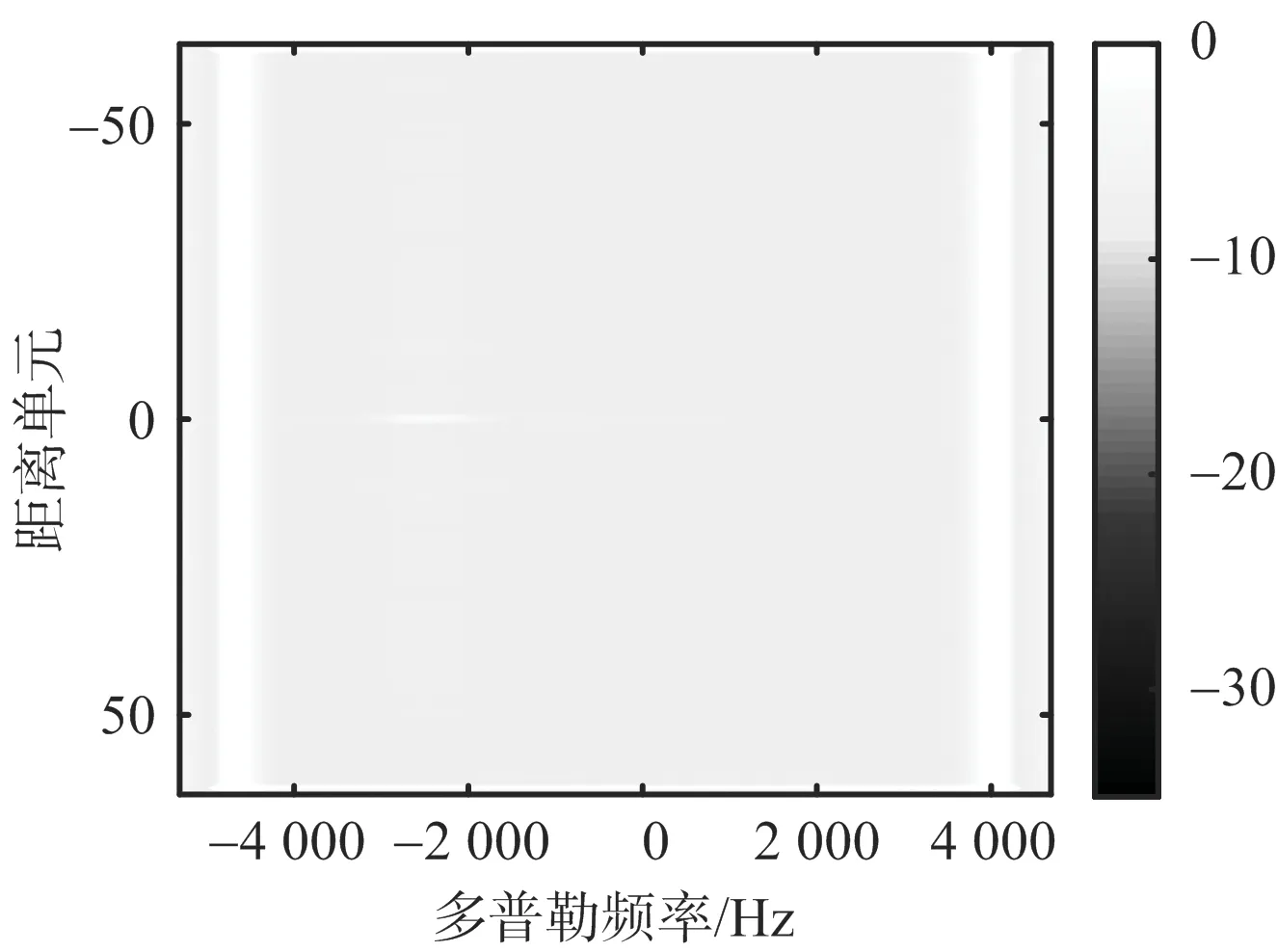
(a) 優化前

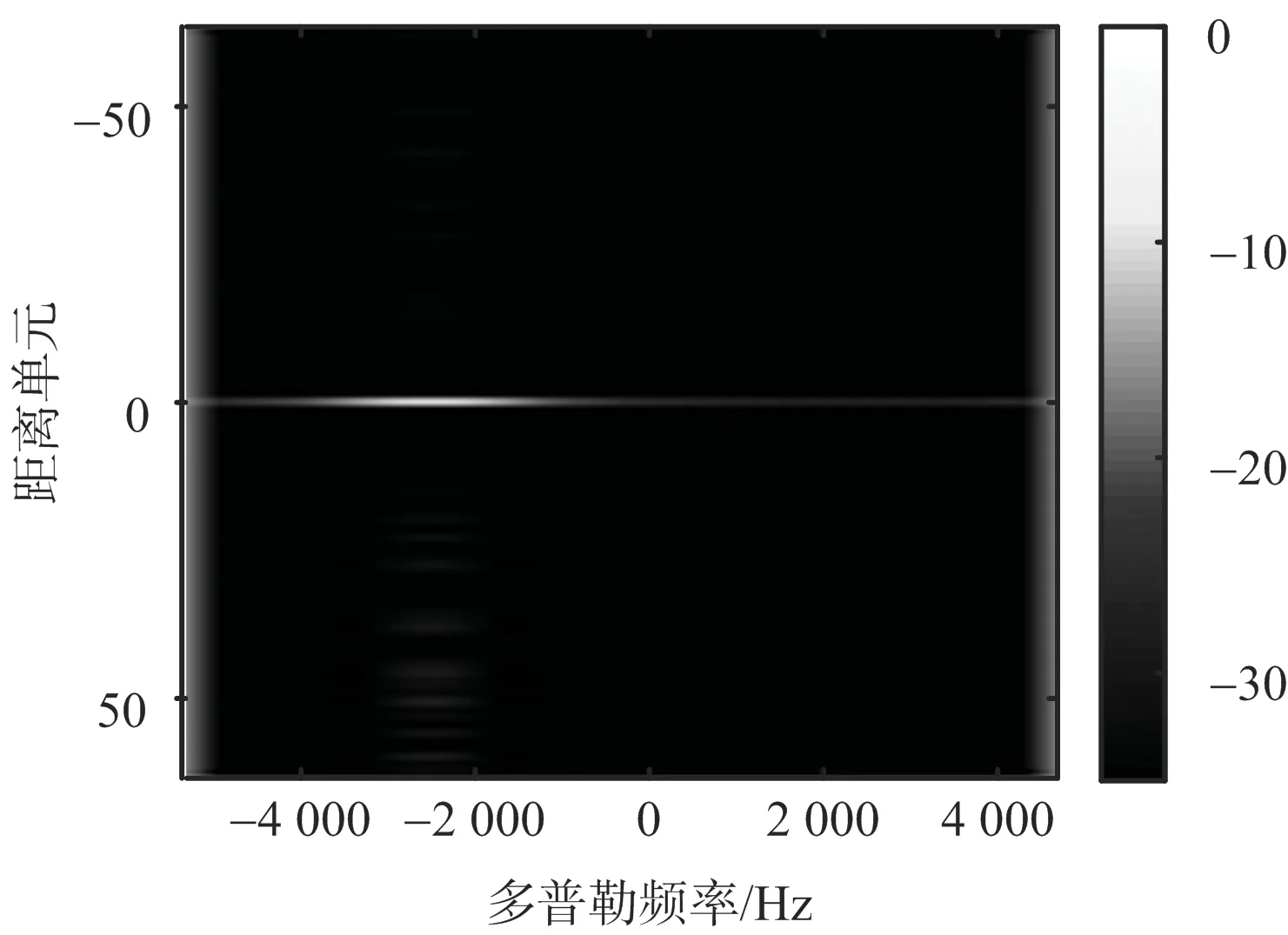
(b) 優化后圖4 二維自適應抗干擾優化模型的模糊函數圖

在一維(脈內編碼)波形設計中，相位編碼的碼長為M。在二維(脈內編碼與脈間編碼)波形設計中，脈沖個數為N，每個脈沖碼長為M。表1為一維(脈內編碼)波形優化和二維(脈內編碼與脈間編碼)波形優化的自由度對比。由表1可見，二維波形優化能夠提高雷達系統的自由度。

表1 一維與二維波形優化自由度對比

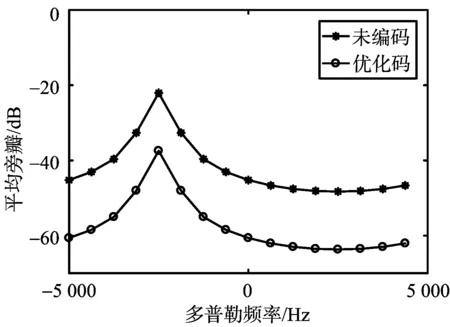
(a) 優化前后平均旁瓣電平

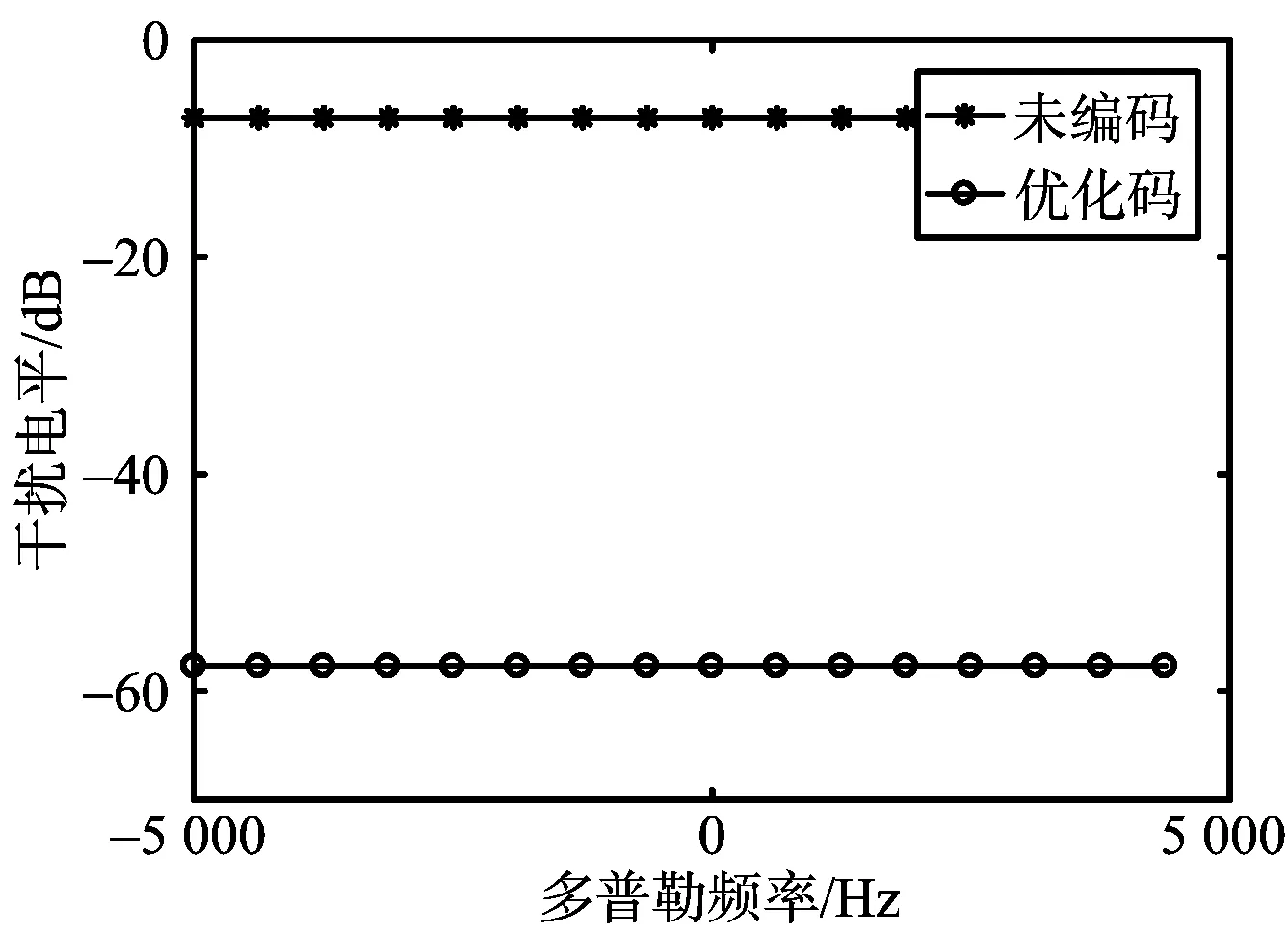
(b) 優化前后干擾電平圖5 優化前后積分旁瓣與干擾電平對比分析

圖5為優化前后輸出端平均旁瓣與干擾信號電平的對比分析。由圖5(a)可知，隨機相位編碼(即未編碼)的平均旁瓣較高。優化后，各通道的旁瓣被抑制，抑制程度在15 dB左右。由圖5(b)可知，未編碼信號對干擾的抑制程度較低，優化信號波形后，輸出端干擾電平下降到-58 dB，干擾抑制程度較高，驗證了算法的可行性。

圖6為不同輸入干信比下輸出端的信干比曲線圖。從優化碼和隨機相位編碼(即未編碼)的對比分析可知，隨著輸入端干信比的增大，未編碼信號的輸出信干比呈下降趨勢，而優化碼的輸出信干比在39 dB左右。

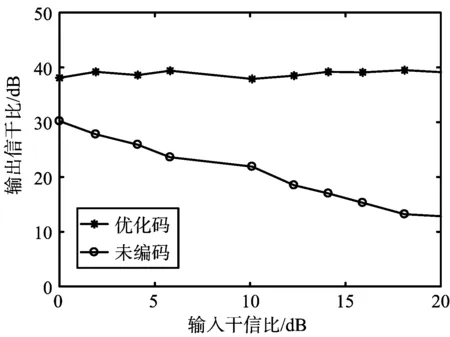
圖6 輸入輸出對比分析

4 結束語

認知雷達采用有效的反饋機制，把接收處理系統“感知”到的目標、場景特征信息反饋到發射端，指導天線系統采用與之“匹配”的發射方式。本文研究認知雷達二維抗干擾波形設計方法，提高了發射端的自由度。首先研究基于模糊函數的發射端二維抗干擾捷變波形調制優化準則和數學模型；其次設計降維策略，將復雜的高維優化問題拆解為多個低維度子優化問題。接著，簡化模型并采用Lagrange乘子法及交替迭代法對模型進行求解，形成完整的二維自適應抗干擾捷變波形調制優化流程和方法。相比較于傳統的單一維度優化波形，該算法的創新點在于二維抗干擾捷變波形能夠從發射端提高雷達系統的自由度。最后通過仿真驗證算法的可行性。