借助“畫數學”彰顯學科本質
——由和的奇偶性探究引發的教學思考

○吳 娟

在教學兩個自然數相加和的奇偶性規律時，我通過創造探索活動，讓學生自主發現和的奇偶性規律。

師：把你和同桌的學號數相加，根據數的奇偶性，會有哪幾種組合？

生：偶數+偶數、奇數+奇數、奇數+偶數

師：相加的和是奇數還是偶數？同桌一起算算看。

……

生：我發現了偶數+偶數=偶數、奇數+奇數=偶數、奇數+偶數=奇數。

師：這僅僅是根據我們剛剛寫出的算式發現的規律，是不是任意兩個不是0的自然數相加，它們的和都有著這樣的奇偶性規律呢？

生：有！

師：這只是我們初步的猜想，你能想到好的方法來驗證我們的猜想嗎？下面我們來小組合作完成這個任務。

……

師：我發現有同學是用畫圖的方法來驗證的。（出示用學生畫圖的方法驗證的作業單，學生自己介紹畫圖驗證的方法。）

師：大家覺得這個方法怎么樣？讓我們一起來回顧這種方法。先用小棒來擺偶數，2個2個的擺，沒有剩余，所以：偶數+偶數=偶數。

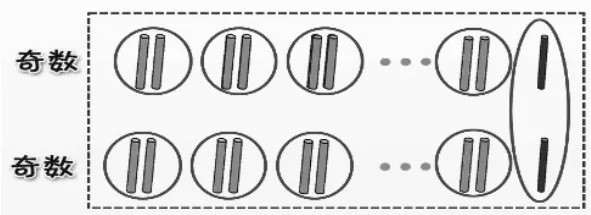
師：而像這樣擺奇數，總會多一個，所以：奇數+奇數=偶數。誰來講一講，為什么？

生：一個奇數多出來的一根加上另一個奇數多出的一根，就湊成兩根，沒有多余了，和是偶數。

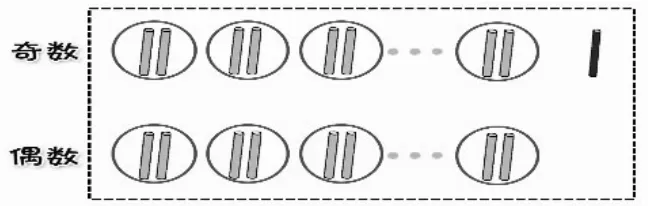
師：偶數+奇數=奇數，誰來講一講？

生：奇數有多余的一根，偶數沒有多余，加起來還是有多余的一根，和是奇數。

在計算規律的探究中，學生為什么會出現用畫圖的方法來驗證？這是基于之前在教學單數和雙數運用了“畫數學”的方法，打開了學生形象思維與抽象思維的通道。一年級的時候認識雙數和單數，我通過畫小棒的方法讓學生明白：用小棒表示一個數，兩個兩個的圈起來，一根都沒有剩余，像這樣的數就叫雙數；兩個兩個的圈起來，最后總有一根剩余，那這樣的數叫單數。這樣從數的本質特征上形象地認識了雙數和單數，也就為以后的奇數和偶數的教學打下了良好的基礎。

“畫數學”就是一種通過畫符號、畫線段、畫簡單圖形，化抽象思維為形象思維，讓學生形成數學建模能力的數學學習方法。它不僅是教與學的一種重要策略，更是一種數學思想。教師應根據對教材和學生的了解，找到數形結合的支撐點，在教學中借助“畫數學”，取得意想不到的教學效果。