面向球幕投影系統的幾何校正方法

王明冬，蓋 孟，賴舜男，王 震

面向球幕投影系統的幾何校正方法

王明冬1，蓋 孟2,3，賴舜男2,3，王 震4

(1. 北京大學深圳研究生院信息工程學院，廣東 深圳 518055；2.北京大學信息科學技術學院，北京 100871；3. 北京大學北京市虛擬仿真與可視化工程技術研究中心，北京 100871；4. 沈陽理工大學，遼寧 沈陽 110159)

用于飛行模擬的視景仿真系統，經常會以多臺投影儀同步投影以得到較大范圍的視場角。當投影機斜對屏幕或者投影屏幕為曲面時，圖像會發生幾何失真。針對此問題，本文提出了一種專門面向球幕投影系統的幾何校正方法，并以一個三通道顯示系統為實例，詳述了該方法的理論原理以及校正流程。實例結果表明，經幾何校正后，各投影圖像無幾何畸變，通道過渡處幾何內容完全一致。該方法是一種純軟件方法，成本小而且操作簡單，能夠適應于不同的投影場景。

球幕；幾何校正；飛行模擬器；多投影；OpenGL

隨著計算機顯卡繪制功能的快速發展，飛行模擬產業也開始蓬勃發展，視覺模擬作為飛行模擬器的所有模擬環節中最貼近飛行員感官的一環，也越來越受到行業內的重視，在整個系統研發中所占據的比重也越來越大。

為了彌補單個投影機視場角不足的限制，一般都會利用多臺投影儀進行聯合同步投影[1-2]，將投影圖像進行拼接，在邏輯上可形成一個全景圖。投影屏幕的形狀多以柱面和球面常見，具有光路設計簡單、成本適中、視場角寬闊等優點，在戰斗機、直升機等飛行模擬器中經常用到[3-7]。相對于柱面、球面在垂直視場方向能夠帶給人更平滑的視覺過渡，因此，在垂直視場角較大的情況下，一般都會選擇球形的投影平面。

一般的投影機都帶有梯形校正功能，可以校正因為投影機斜對屏幕導致的透視形變。但當屏幕是曲面時，大多數投影機都無法正確處理，此時就需要使用其他方法對投影畫面進行幾何校正[8]。

目前，軟件幾何校正方法主要有RASKAR等[9]提出的矩陣映射方法，及多項式函數校正方法[10]等，其均通過相機采集反饋圖像，并在二維平面內進行矩陣映射或多項式插值計算實現幾何校正，使用不夠靈活方便，計算量相對較大。

鑒于上述情況，本文以某飛行模擬器視景仿真系統為實例，提出了一種針對球形投影幕的軟件幾何校正方法，并詳細描述了其流程和原理。該方法不需要增加額外的硬件設備，成本低、粒度小，可以作為視景系統的一個內部子系統進行嵌入且不影響繪制效率。同時，該方法可擴展性高，對于規則二次曲面，可通過細微的改動達到校正的效果。

圖1為實例系統的整體架構，系統包括了一個主系統和多個從系統(圖中只展示了2個)。通信子系統負責與主控對接，將主控傳來的信號翻譯并發送給多機同步子系統，多機同步子系統負責各個通道之間的繪制同步，在每幀開始時，分發來自通信子系統的繪制信號，結束時，發送圖像刷新指令，所有機器同時將圖像送往投影機進行投影[11]。曲面校正子系統負責對繪制子系統生成的圖像進行扭曲處理，該扭曲處理使得圖像經過投影儀投射到球面上剛好形成正常透視的圖像。融合子系統負責對各個投影機投影的重合部分的亮度進行由明到暗的過渡處理，使整個視景在融合區域平滑過渡。

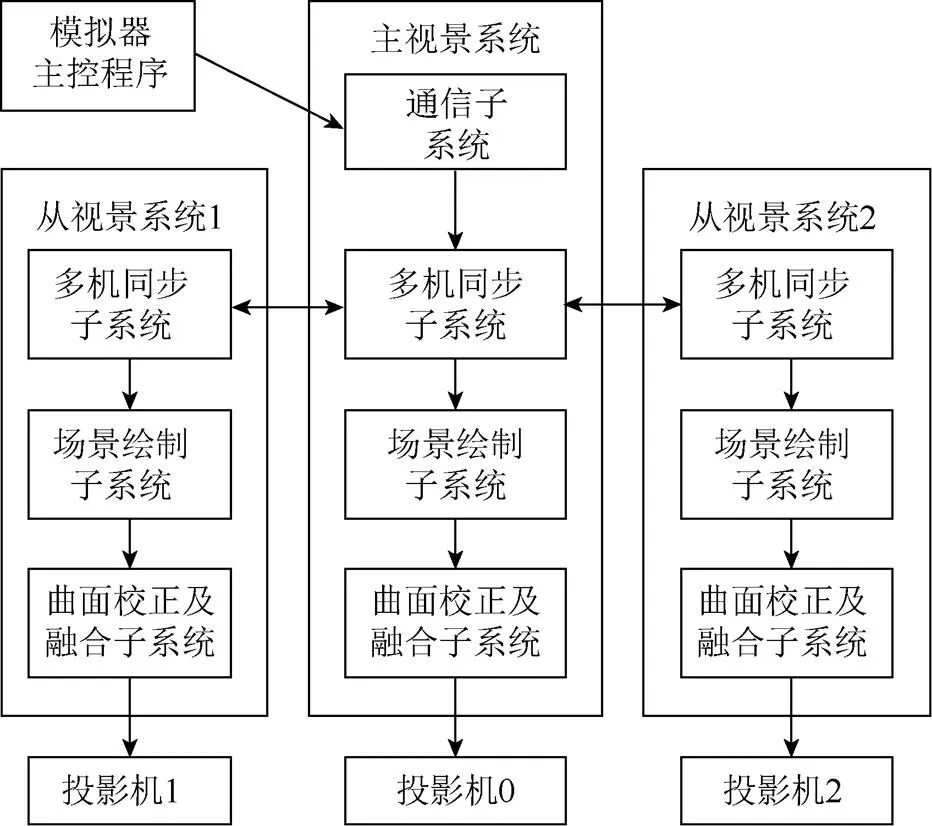
圖1 視景系統整體架構[12]

曲面校正方法的流程如下：

(1) 給投影平面建立參數化表達，并以參數為度量，劃分每臺投影儀的投影范圍及融合區域。

(2) 利用交互式程序，對輸入圖像和球面上投影點的映射關系進行擬合。

(3) 針對每臺投影儀的投影范圍，計算對應視景通道的視錐參數。

(4) 確定曲面校正子系統中的扭曲處理算法。

1 投影區域的參數化表達

在計算機上存儲一個球面是相當困難的，若將球面離散成一些小片也是相當復雜的。因此，在計算機圖形學領域，一般采用球面經緯映射圖像的方法描述一個球面，也就是將球面上的點按照經緯度映射到一個矩形紋理上，經度()映射成矩陣的水平坐標，緯度()映射成垂直坐標。但是該映射會產生水平方向的拉伸問題，赤道上的比例是正常的，越靠近兩極，拉伸越嚴重，在極點處一個點變成了一條線。在大多數情況下，經緯度映射還是相當好用的。

事實上，常見的矩形地圖就是經緯度映射圖像。當映射整個球面時，由于球面的經度范圍比緯度范圍多一倍，將得到一個長寬比為2∶1的矩陣。圖2展示了球面上的點和在經緯映射平面上對應點的關系。

在實例系統中，投影平面是一個半徑為3 m，經度跨幅約230°，緯度范圍從約–30°~+30°的球帶。由3臺投影儀排成一行進行投影，中間的投影通道為主視景系統，兩側為從視景系統。飛行員的眼點位置處于球心處。以飛行員眼點位置為原點，右手方向為軸正方向，豎直向上為軸正方向建立飛行員觀察坐標系eye–。不失一般性，記球心在觀察坐標系下的坐標為(center,center,center)，顯然，飛行員眼點不可能出現在球外，因此必然有

圖2 經緯度映射示意圖

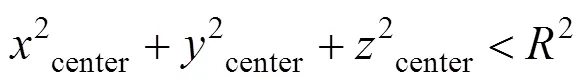
參考觀察坐標系，建立球面的經緯度坐標，球面上點到觀察坐標系的變換關系為

依據每臺投影儀的投影范圍上限，將其裁減為經緯度坐標系下的矩形。裁剪后，3臺投影儀投影緯度范圍為–30°~30°，從右向左3臺投影儀投影的經度范圍依次為[–115°, –35°]、[–50°, 50°]、[33°, 113°] (投影儀自右向左，投影范圍自左向右)。

2 投影儀投射關系的擬合

為找到并記錄輸入圖像到投影曲面之間的映射關系，使用參考文獻[13]的方法，用貝塞爾曲面擬合其逆映射，即為投影曲面到輸入圖像的變換關系[13]。

×次的二維貝塞爾曲面的表達形式為[14]

其中，K,j為曲面的控制點；B,m()和B,n()是混合函數伯恩斯坦多項式，即

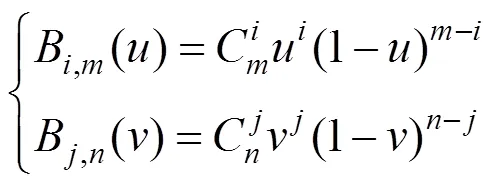
將(,)當作投影曲面參數歸一化后的坐標，(,)當作輸入圖像的坐標，式構成了從投影曲面向輸入圖像空間的映射。

需尋找到(+1)×(+1)個控制點，使得由此生成的貝塞爾曲面與投影曲面基本吻合即可。實踐表明，在大多數情況下，對于球面投影拼屏幕，取4×4階貝塞爾曲面就能夠得到較佳的結果>[13]。利用交互式程序可完成該過程：

(1) 將球面參數和歸一化到[0,1]范圍，變為和。隨后對和分別進行和等分，加上端點總共能夠得到(+1)×(+1)個不重復的目標點(u,v)(0≤≤,0≤≤)。

(2) 利用交互式程序調整上一步得到的關鍵點坐標對應的(u,v)的位置，使得(u,v)正好投射在參數(u,v)所對應的球面位置，同時利用式實時反解K,j的值，重構整個曲面；此時發現，生成的曲面已經與投影幕的參數曲面足夠吻合。

圖3為實例系統的中間通道的擬合結果以及兩邊通道的部分結果，顏色較深的部分為重合區域。取4×4階貝塞爾曲面，每臺投影機輸出的曲面60等分，第0，15，30，45，60個等分格處為選中的用來重構曲面的關鍵點。圖4為中間通道的貝塞爾曲面在輸入圖像空間的呈現。至此，已經得到了表示投影曲面到輸入圖像之間變換關系的貝塞爾曲面，只需簡單地用(,)作為頂點位置，(,)作為輸出數據，創建且光柵化貝塞爾曲面的細分網格，得到的圖像記錄了從輸入圖像到投影曲面的映射關系。

圖3 擬合結果

圖4 中間曲面在圖像空間的展示

3 視錐參數的計算

計算各個通道的視錐參數，使視景的繪制子系統利用此視錐參數以及多機同步子系統發送的相關參數，計算觀察矩陣以及透視投影矩陣，進行場景的繪制。

若某個通道的投影范圍為[,]× [,]，要計算視錐參數，需要首先確定攝像機觀察坐標系O–。

在OpenGL中，一般用攝像機位置、上方向以及觀察方向3個向量來確定觀察坐標系，并依次考慮其設置。除特殊情況，均應該將攝像機位置與飛行員觀察坐標系原點重合。任何經過攝像機的直線，在飛行員眼中均可投影成一個點。對于圖像的像素點，在進行幾何校正時，可不考慮該點的深度信息，因為其深度不會影響人眼中的成像位置。

在實例系統中，這種緯度范圍離兩極球帶較遠，可以簡單地讓上方向和飛行員觀察坐標系的軸重合。其好處是做透視投影時，經度線會投射成一條平行于軸的直線，計算視錐時會較方便。

接下來需考慮觀察方向的設置，觀察方向是垂直于上方向的，因此必然是水平的。生活中人們知道，正視一個物體時，看的最清晰。因此，想要得到一個好的透視投影效果，觀察方向應該垂直于觀察平面，但是對于球面，很難定義其垂線方向。一般情況，可將其設置為一個變量，定義域為從觀察坐標系原點出發，所有與投影范圍相交射線的方向。用戶通過調節其值，得到最好的投影效果。

實際上，對于某些在垂直視場方向要求比較高，甚至投影區域包含了北極點的情況，幾何校正系統可規定攝像機觀察坐標系的原點，上向量和觀察向量均作為參數，交給用戶去調節。考慮到攝像機觀察坐標系原點和飛行員眼點是重合的，而且同是右手空間直角坐標系，可用歐拉角中的和作為參數，用戶可對其進行調節。攝像機觀察坐標系是通過飛行員觀察坐標系做相應的歐拉旋轉實現的。記飛行員觀察坐標系到攝像機觀察坐標系的變換矩陣為，則坐標變換關系為

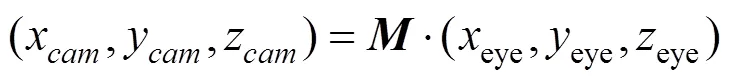
對于實例系統，因為飛行員眼點處于球心，可簡單的將飛行員觀察坐標系繞沿自身軸順時針旋轉(+)/2.0，變為該通道的新的觀察坐標系。

從兩方面考慮視錐的設置：①為了保證投影區域內的顏色均有意義，該通道在球幕上的投影范圍必須都在視錐的裁剪范圍之內；②對于無效像素點的繪制，會造成計算機資源的浪費。理想情況下，該通道的視錐和球幕投影區域在近裁剪面上的投影應該是重合的，但實際上，經緯度參數下的矩形區域投射到空間直角坐標系，并不會是一個矩形，所以二者不可能完全重合。只能選取球幕在近裁面的投射區域的外接矩形，作為視錐范圍。可以通過式和式將球面的經緯度坐標點變換為攝像機坐標系，將定義域限定為投影范圍，求出對應值域的范圍即得到了視錐范圍。

圖5為正前方半球的經緯網在近裁剪平面上的透視投影，可以很清晰地看出，在近平面上，經線會投射成一條平行于軸的直線，緯線中赤道會投影為一條平行于軸的直線，其余的緯線中心向赤道凹曲。

圖5 經緯網的透視投影

在OpenGL中，一般會用，，，，，6個參數來確定透視投影矩陣。其中，和為近裁剪面和遠裁剪面與視點的距離，，，，為視錐在近裁剪平面上的投影。由6個參數，確定了視錐的6個裁剪平面，相對于幾何校正而言，只需要關注左右下上4個裁剪平面即可，而期只和，，，與的比值有關，因此只需要計算該4個比值即可。可將4個比值記為，，，，即

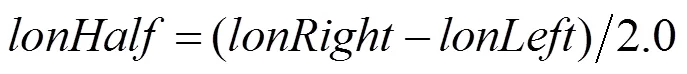
根據和的正負性，簡單的分為3種情況：

(1) 當0≤<時

(2) 當<0≤時

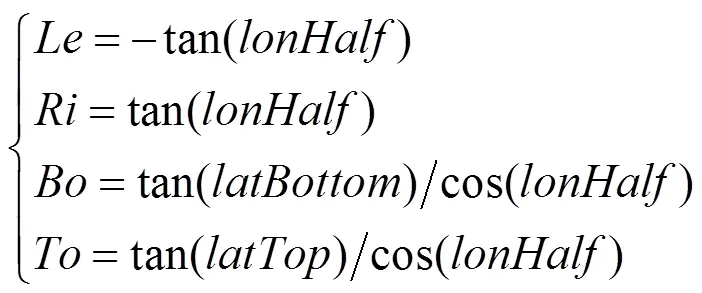
(3) 當<<0時

4 扭曲處理算法

對繪制子系統生成的圖像進行扭曲處理，使其經過攝影儀投射到球幕上，顯示出正確的結果。

如圖6所示，為球幕上的一個點，投影儀會將輸入圖像的點投影到處，而在正常情況下，飛行員在點看到的應該是近裁剪平面上點的圖像。因此，只需將近裁剪平面上點的像素顏色賦于輸入圖像所在的位置。這樣，經投影儀投影后，飛行員即可在點看到正確的結果。

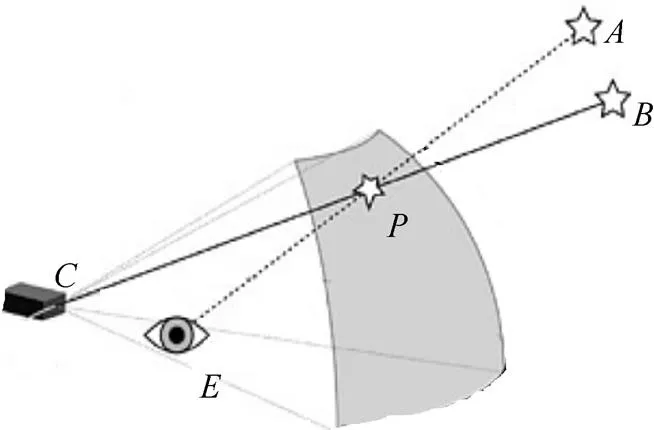
圖6 扭曲處理示意圖

對于輸出圖像的每一個像素，通過在第2節擬合的投影儀映射關系，很容易判斷出該像素是否會被投射到限定的投影區域。若否，直接將該點的亮度設為0，繼續處理下一個像素，反之，能夠獲得投影點的歸一化參數坐標值，對其進行歸一化的逆操作，便得到該點在球幕的投影點的經緯度坐標(,)。利用式和式，將其變換到觀察坐標系，再通過第3節得到的透視投影矩陣以及齊次變換，即可得到應該被扭曲到點的像素點的紋理坐標。

對于實例系統，將視錐參數，代入式，便可得到

將輸出圖像由投影儀進行投影，即可得到正確的圖案。圖7為不做幾何校正前的視景圖像，圖8和圖9為校正后的視景圖像。

圖7和圖8是相同視角下的2張圖，通過對比，可以發現圖7中，2臺投影儀的過渡處幾何內容未完全匹配；圖8則沒有這種現象。圖9在整體上對幾何校正的結果進行了一次展示，可以看出，3個通道的視景圖像均已解決了幾何畸變的問題，在相鄰通道的過渡處，圖片的幾何內容完全重合。

圖8 幾何校正后的視景1

圖9 幾何校正后的視景2

5 結束語

本文針對面向球形投影幕的飛行模擬器視景仿真系統，提出了一種簡單、靈活、高效的軟件幾何校正方法。對比其他的軟件幾何校正方法[8-10]，有以下主要優點：

(1) 校正無需相機的采集反饋，工作量小。本文所述的幾何校正方法只需一次校正預處理，無需相機的圖像采集反饋就能實現幾何校正。對比于矩陣映射以及多項式插值的校正算法，計算復雜度可以忽略不計，實時性高。

(2) 校正方法靈活，適用性強。該幾何校正方法不關注投影儀是否正投，且只需簡單地改變投影幕參數化表達方法，就可以適用于其他的二次規則曲面，適用性強、易于推廣。

[1] FERREIRA F T, KURASHIMA C, CABRAL M C, et al. A small-scale and flexible platform for multi-projector systems development [C]//2013 XV Symposium on Virtual and Augmented Reality. New York: IEEE Press, 2013: 216-219.

[2] SONG Z J, GONG G H, HUANG Z P, et al. A new edge blending paradigm for multi-projector tiled display wall [C]//2010 International Conference on Computer Application and System Modeling (ICCASM 2010). New York: IEEE Press, 2010, 5: V5-349-V5-352.

[3] 周章勇. 一種三通道球帶幕視景系統的開發[J]. 航空維修與工程, 2018(8): 30-33.

[4] PORTALéS C, ORDU?A J M, MORILLO P, et al. An efficient projector calibration method for projecting virtual reality on cylindrical surfaces [J]. Multimedia Tools and Applications, 2019, 78(2): 1457-1471.

[5] FURUKAWA R, NAITO M, MIYAZAKI D, et al. Auto-calibration method for active 3D endoscope system using silhouette of pattern projector [C]//Image and Video Technology. Heidelberg: Springer, 2018: 222-236.

[6] 鄧晴鶯, 李國翬, 王寶奇, 等. 某飛行模擬器視景系統的設計與實現[J]. 兵工自動化, 2016, 35(8): 75-79.

[7] 鄧晴鶯, 李國翬, 王寶奇, 等. 大下視場飛行模擬器視景系統的設計與實現[J]. 系統仿真技術, 2016, 12(2): 123-129, 139.

[8] BROWN M, MAJUMDER A, YANG R. Camera-based calibration techniques for seamless multiprojector displays [J]. IEEE Transactions on Visualization and Computer Graphics, 2005, 11(2): 193-206.

[9] RASKAR R, BROWN M S, YANG R G, et al. Multi-projector displays using camera-based registration [C]//Proceedings Visualization '99. New York: IEEE Press, 1999: 161-168.

[10] 劉立坤, 劉海波. 廣角攝像機標定及畸變圖像修正方法研究[J]. 艦船電子工程, 2018, 38(5): 77-80.

[11] 趙永強. 直升機飛行模擬器視景仿真系統的設計與實現[D]. 北京: 北京郵電大學, 2010.

[12] 董鴻鵬, 王春財, 張波. 飛行模擬器視景系統的設計與實現[J]. 計算機應用, 2018, 38(S1): 228-231, 235.

[13] 徐澤驊, 李勝.面向大規模戶外場景的實時繪制系統[D]. 北京: 北京大學, 2017.

[14] AHMED A. Geometric correction for uneven quadric projection surfaces using recursive subdivision of Bézier patches [J]. ETRI Journal, 2013, 35(6): 1115-1125.

Geometry Correction Method for Projection onto Spheres

WANG Ming-dong1, GAI Meng2,3, LAI Shun-nan2,3, WANG Zhen4

(1. School of Electronic and Computer Engineering, Peking University Shenzhen Graduate School, Peking University, Shenzhen Guangdong 518055, China; 2. School of Electronics Engineering and Computer Science, Peking University, Beijing 100871, China; 3. Beijing Engineering Technology Research Center of Virtual Simulation and Visualization, Peking University, Beijing 100871, China; 4. Shenyang Ligong University, Shenyang Liaoning 110159, China)

A visual simulation system for flight simulation often uses multiple projectors to simultaneously project a surface to obtain a wider range of viewing angles. When the projector is tilted to the screen or the projection screen is a curved surface, the image is geometrically distorted. Aiming at this problem, this paper proposes a geometric correction method for the dome projection system. Taking a three-channel display system as an example, the present study describes the theoretical principle and correction process of the method in detail. The example results show that after geometric correction, each projection image has no geometric distortion, and the geometrical content of the channel transition is completely consistent. The method is a pure software method, which is small in cost and simple in operation, and can be adapted to different projection scenarios.

sphere; geometry correction; flight simulator; multiple projections; OpenGL

TP 391

10.11996/JG.j.2095-302X.2019040631

A

2095-302X(2019)04-0631-06

2019-03-26；

定稿日期：2019-04-11

國家自然基金重點項目(61632003)；國家自然基金面上項目(61872398)；裝備預研基金項目(315050501)；國家重點研發計劃課題(2017YFB1002601)

王明冬(1994-)，男，甘肅白銀人，碩士研究生。主要研究方向為計算機圖形學。E-mail：wmd@pku.edu.cn

賴舜男(1965-)，女，重慶人，工程師，碩士。主要研究方向為虛擬仿真。E-mail：snlai@pku.edu.cn