大時間步長下體積守恒的實時水體模擬

朱奎鑫，蓋 孟，賴舜男

大時間步長下體積守恒的實時水體模擬

朱奎鑫1，蓋 孟2,3，賴舜男2

(1. 北京大學深圳研究生院，廣東 深圳 518055；2.北京大學信息科學技術學院，北京 100871；3. 北京大學北京市虛擬仿真與可視化工程中心，北京 100871)

基于物理的流體仿真可以真實地捕捉水的運動，一種常用的實時模擬方法是基于二維淺水方程進行水體仿真。首先介紹了二維淺水方程，并提出一種新的求解方法，通過一種體積守恒的隱式半拉格朗日方法進行計算，在保持穩定的同時允許較大的時間步長，然后額外增加修正步以保證計算過程中體積守恒。此外提出了一種基于動量守恒的流固耦合方法，可以實時地模擬出較為真實的水體，并且保證了水體體積始終守恒，效果良好。

淺水方程；半拉格朗日；體積守恒；大時間步長；流固耦合

流體運動是一個復雜的現象，很難實時在計算機上進行有效模擬，折中的方法是通過模擬水面來近似模擬水體，只需要使用二維區域上的高度場即可進行實時模擬。常用的方法有2種，一種是基于譜的模擬[1]，此方法非常穩定且細節豐富，但缺點是難以與移動的障礙物相互作用；另一種是使用基于物理的淺水方程進行模擬。本研究以二維淺水方程組為基礎，提出了一種高效、穩定、體積守恒的流體仿真算法。通過半拉格朗日方法的使用，實現了較大的時間步長下的穩定模擬，這種基于物理的流體模型能夠產生真實的波運動，對流體做到實時合理的仿真。

本文首先對淺水方程進行了描述，以此為基礎建立了流體仿真模型。淺水方程是由納維-斯托克斯方程推導而來，雖然無法模擬三維流體或帶有黏度的流體，但是由于在高度項上進行了簡化，計算量大大降低，使得求解效率提高，可以實現對流體的實時模擬。

然后，詳述了一種質量守恒的半拉格朗日方法。人們知道，常規的半拉格朗日方法無法做到質量守恒，無法滿足物理仿真與實際相符，通過在常規方法之后進行的擴散操作的改進，保證了平流前后質量守恒，對于流體仿真具有重大意義。

之后，對基于二維淺水方程的流體仿真進行實現。在該模型中，采用改進的隱式半拉格朗日積分法求解，再使用修正步彌補求解時的體積損耗，在保證穩定性的同時，允許較大的時間步長。

在此模型上實現了流固耦合的技術，借助有向距離場來判斷交互區域，然后基于動量守恒進行單向交互，取得了很好的效果。

最后，通過演示該模型展示流體模擬的效果，并與其他模型進行了比較，證明了本文方法體積守恒、算法穩定、計算效率高。

1 淺水方程

淺水方程是描述淺水流動的數學模型，常用于實時流體運動的仿真計算。在流體動力學中，通常水平長度比垂直長度大得多，在此條件下，可以得到沿水深方向的靜水壓力分布，并根據納維-斯托克斯方程導出淺水方程。有時也會引入水深方向的平均化，導出淺水方程的另一種形式。本文使用的淺水方程式為

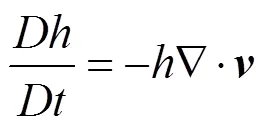
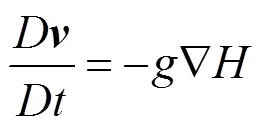
其中，為水平面高度；為水的深度，即水平面高度減去地形高度；為速度；為重力加速度；為時間。

淺水方程沒有黏性項，水的深度方向速度可忽略，所以模擬時僅限于二維無黏流體，對于高黏度流體，飛濺或破裂的流體無法模擬。然而，其可充分地模擬一大類流體的運動，且計算效率極高，是進行實時流體模擬的最好選擇。

求解淺水方程有多種方法，中外研究者大都采用有限體積法以保證體積守恒[2-3]，不過該方法在較大時間步長下表現不穩定；有些隱式差分方法，可以保證無條件穩定[4]，卻不能保證體積守恒，本文方法希望可以同時具有這2個優點。

2 半拉格朗日方法

半拉格朗日方法[5]可以看作是歐拉方法和拉格朗日方法的混合體。歐拉方法保持網格的規則性，但為了保持穩定，需要較小的時間步長。拉格朗日方案不受穩定性要求的限制，允許更大的時間步長。半拉格朗日方法試圖將2種方案的優點，即歐拉方法的規則性和拉格朗日方法的穩定性結合起來，在每個時間點，進行網格點值計算時，沿著粒子軌跡進行求解。

以式(1)為例，等式左邊展開為

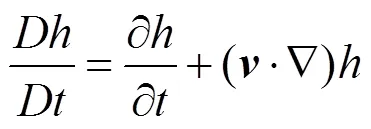
公式右邊的第1項稱為局部項，第2項為平流項。其實，半拉格朗日法就是用拉格朗日的思想求解平流項，然后在固定的網格上求解局部項。

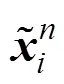
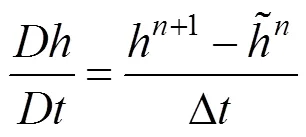
類似的，有

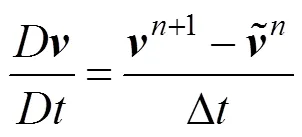
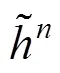
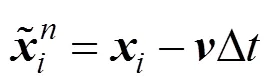
其中，為當前時刻網格的速度。

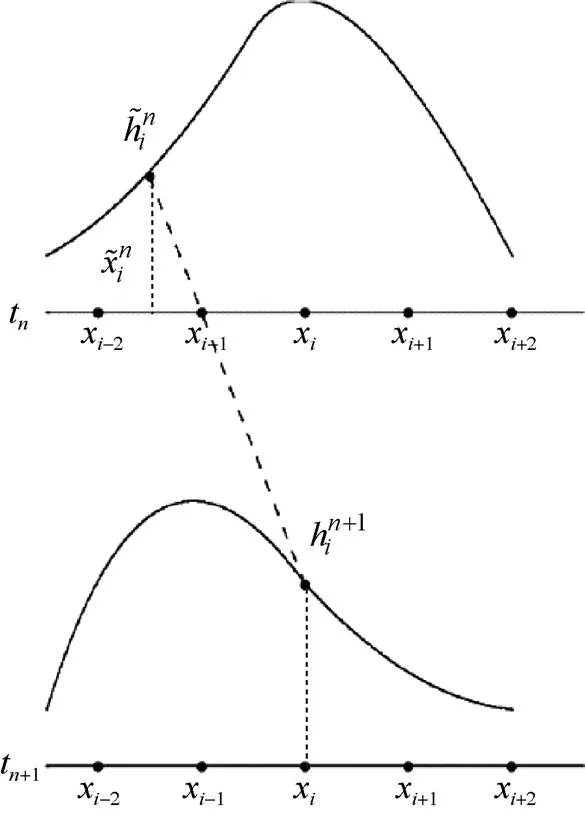
圖1 半拉格朗日方法

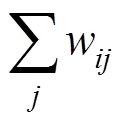
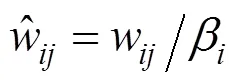
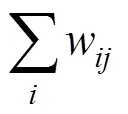
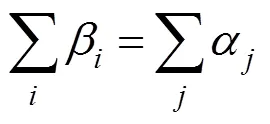
圖2中的()和偽代碼中的()代表的是α，為每個網格的流入量權重，而()代表的是網格存儲的物理量。在循環過程中，α逐漸向1靠攏。

上述擴散權重的方法，也存在一個問題，即迭代次數過多，對實時仿真造成影響。一種加快該過程的方法是繼承上一次的誤差，在每幀權重擴散之前，加上上一幀最后計算的結果與1的差，然后再進行權重擴散。在實際工作中，這樣可以減少迭代次數，提高仿真效率。

圖2 擴散權重方法

3 方程求解

進行方程求解模擬流體運動的流程如下：

(1) 使用本文改進的半拉格朗日方法進行平流。

(2) 將方程離散化，隱式求解。

(3) 考慮求解中損失的體積，在修正時進行體積補償。

3.1 半拉格朗日平流

半拉格朗日平流，使用本文改進的半拉格朗日方法，滿足任意β和α均等于1的條件，這樣既保證了體積守恒，也實現了較合理地仿真效果。使用了繼承誤差的方法后，在仿真過程中，迭代次數不超過10次即可收斂，可既達到目的，也滿足了的實時仿真的要求。

3.2 隱式求解

在進行平流之后，部分研究者采用半隱式的方法[8]，本文采用文獻[9]隱式求解的方法，1階精度，但對于流體模擬已經足夠，式(1)和式(2)可以寫成如下形式

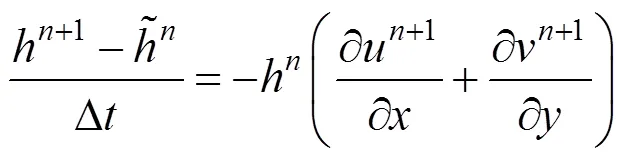
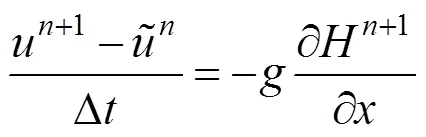
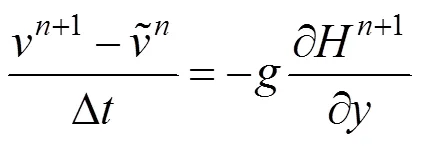
式(7)~(9)中，為速度方向的分量；為速度方向的分量。由于采用隱式求解，所以等號右邊均使用了下一時刻的狀態，式(7)等號右側的h，本應為h+1，但這將變成非線性方程組求解問題，求解困難，因此本文使用h來近似h+1。

現在開始討論網格如何離散化。在整個模擬過程中，必須在空間的各個點存儲許多不同的量(速度、高度等)。很明顯，需要采用一種合理的布局。最簡單的方法是，將所有信息存儲在同一個網格中心上，但這并不是最佳的方法。很早以前，MAC網格就被提出[10]，目前在流體模擬中被廣泛使用。該網格也被稱為交錯網格，因其在不同的位置存儲不同的物理量，如在網格中心存儲高度，網格邊上存儲速度。在二維情況，MAC網格中的單元格結構如圖3所示。

根據這個網格結構，可將高度、速度相關的公式進行空間離散化，形式如下

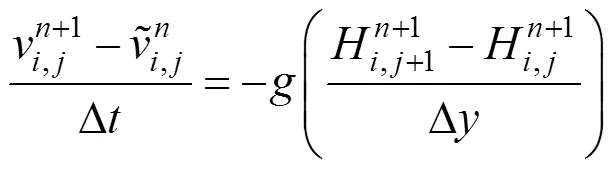
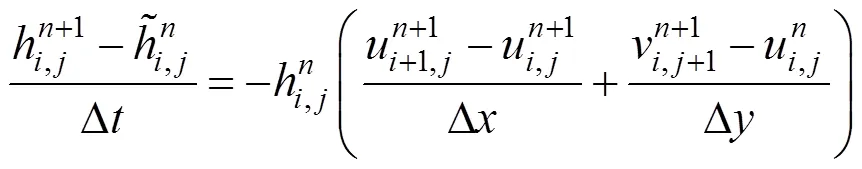
將速度公式帶入到高度公式中即可得到一個線性方程組，使用雅克比迭代求解該大型稀疏線性方程組，時間步長較小時，迭代10次以內就可以得到滿意的結果。

3.3 體積修正

在實現的流體模擬中，每一步都要保證體積守恒。平流時采用了改進的半拉格朗日方法，保證了平流前后體積守恒，但是在進行隱式求解時，無法保證體積守恒，為此，需要找到求解過程中的體積損失。

根據高度公式，不難發現，如果要保證最后體積守恒，線性方程組的所有方程等號右側相加應該等于0，隱式求解時的方程組并未滿足該條件，所以體積不守恒。現在要對體積進行修正，在更新高度時，等號右側統一地加入一個相同形式的量，使得所有網格等號右側相加等于0。

通過上述描述已可以實現在開闊區域的水面模擬，如圖4所示。

圖4 水面上的水波

3.4 邊界處理

干濕邊界處理在淺水方程中也很重要，有很多方法得到了廣泛應用[11]，將邊界進行標記，然后特殊處理。對于本文的模擬來說，在水流開始運動之前，有水的網格水平面應該高于附近沒有水的網格地形。否則，兩者之間的面就被標為障礙。對于在MAC網格中標記為障礙的面，速度在每個時間步結束時設置為0，而且在平流步中不更新。滿足以下條件的面視為障礙，即

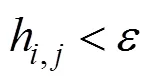
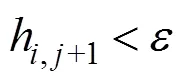
其中，為一個大于0的小常數，均定義為0.000 1。類似的情況也適用于交錯網格的其他面。按照本文的處理方法，圖4所示的水體碰到邊界后如圖5所示。

圖5 水波碰到邊界

3.5 流固耦合

流固耦合在水體模擬中是一個重要的話題，為了使剛體與水體之間能有效地相互作用，本文提出了一種模擬流固相互作用的單向耦合方法，即水體的運動只能受到剛體的影響，而不對剛體的運動產生影響。

流固耦合有2個關鍵技術，一是如何確定交互區域，二是確定交互區域之后的相互作用。

使用有向距離場來確定交互區域。有向距離場(signed distance field, SDF)，“有向”、“距離”、“場”這3個詞非常精確的描述了SDF究竟是什么。SDF是到(多邊形模型)物體表面最近距離的采樣網格。距離的正負號表示在物體的外部或內部，距離值為正表示點在物體外部，反之在內部，若距離值為零表示點在物體表面。可將交互的固體模型文件轉化為有向距離場。對于淺水方程的每個網格，可對高度進行離散，依次就此網格的當前高度判斷距離值是否為負，并判斷是否在交互物體內部。如果在交互物體內部，那么此網格的當前高度就是交互區域，這樣，在二維的水面上得到了一個三維的交互區域。

確定交互區域之后，根據動量守恒進行交互。對于當前網格，如果處于交互區域，認為交互區域的速度等于固體的速度。然而，由于交互區域是三維的，可能某些高度處于交互區域，或不屬于交互區域，但是對于當前網格，只有一個速度，即

其中，1為固體速度；2為交互之前的水體速度；3為交互之后的水體速度；1為當前網格根據深度離散化后，處于交互區域的高度和；2為不處于交互區域的高度和；3為水深，1+2=3。

交互算法流程如下：

步驟1.對于交互的固體模型轉化為有向距離場。

步驟2. 對于每個時間步長：

(1) 確定有向距離場在整個計算網格上的大致投影區域。

(2) 對于投影區域的每個網格：①將網格上的高度離散化，從上到下遍歷每一個離散坐標，判斷坐標點是否在物體內部；②對每個網格，按照動量守恒，更新當前網格速度。

(3) 繼續進行淺水方程計算。

按照此方法，水面上劃過的木塊尾跡，如圖6所示。

圖6 水面上的劃過的木塊

4 結果和分析

4.1 實驗結果

本文模型可以模擬許多的流體運動。為了滿足實時要求，還借助了GUDA進行GPU并行加速。所有的流體模擬都是在CPU為inter(R) Core(TM) i5-4570 3.20 GHz，顯卡為NVIDIAGeForce GTX970，操作系統為Windows10，使用CUDA9.1進行并行加速計算。

圖7使用固定的邊界，對帶有障礙物的矩形水池中的水波進行了實時模擬。此實驗中模擬的網格大小為256×256，每幀間隔為0.1 s。

圖7 矩形水池中的水波

本文的模型是基于物理的，因此只需要為其提供一組初始條件，也就是模擬開始時水面的形狀，水面就會根據淺水方程自然演變。圖8是水從柱子間流出，較為真實地模擬了水體效果。

圖8 柱子間的水流

由于本文采用隱式半拉格朗日解法，可以使用較大時間步長進行模擬，與較小時間步長相比，效果近似，但速度提升較快。圖9是時間步長分別為0.1 s和1.0 s的2個實驗結果對比。在時間步長較大的情況下，隱式求解迭代次數增多，在保證體積守恒的情況下，依然可以保持實時模擬。時間步長為0.1 s和1.0 s時，模擬100幀的時間，分別為26 s和17 s。

圖9 不同時間步長 (左側為0.1 s，右側為1.0 s)

關于固體與水體之間的交互，從效果上看還是很好的，較好地模擬了固體對水體的作用力，如圖10所示。

圖10 水面上行駛的小船

4.2 比較與分析

顯式方法由于其簡單性，被用于流體模型的許多實現中。但其主要缺點是對時間步長有嚴格的限制，數值解可能與真實解呈指數發散。通過選擇隱式積分方法，保證了穩定性不受梯度項大小的限制。通過采用半拉格朗日方法，還確保了時間步長不受CFL條件的限制。只要有足夠的精度估計出發點，可確保算法是穩定的。比較該算法與采用半拉格朗日方法的算法的穩定性，以2010年CHENTANEZ和MüLLER[12]的算法作為比較，其通過有限體積法同樣實現了體積守恒。兩者之間的效果對比如圖11所示，初始場景是3個水柱，2種方法的效果基本相同。在本文的測試案例中，隱式半拉格朗日方法得到的最大時間步長比文獻[12]方法大10倍以上，本文的CFL數在超過10時依然保持了模擬的穩定性。

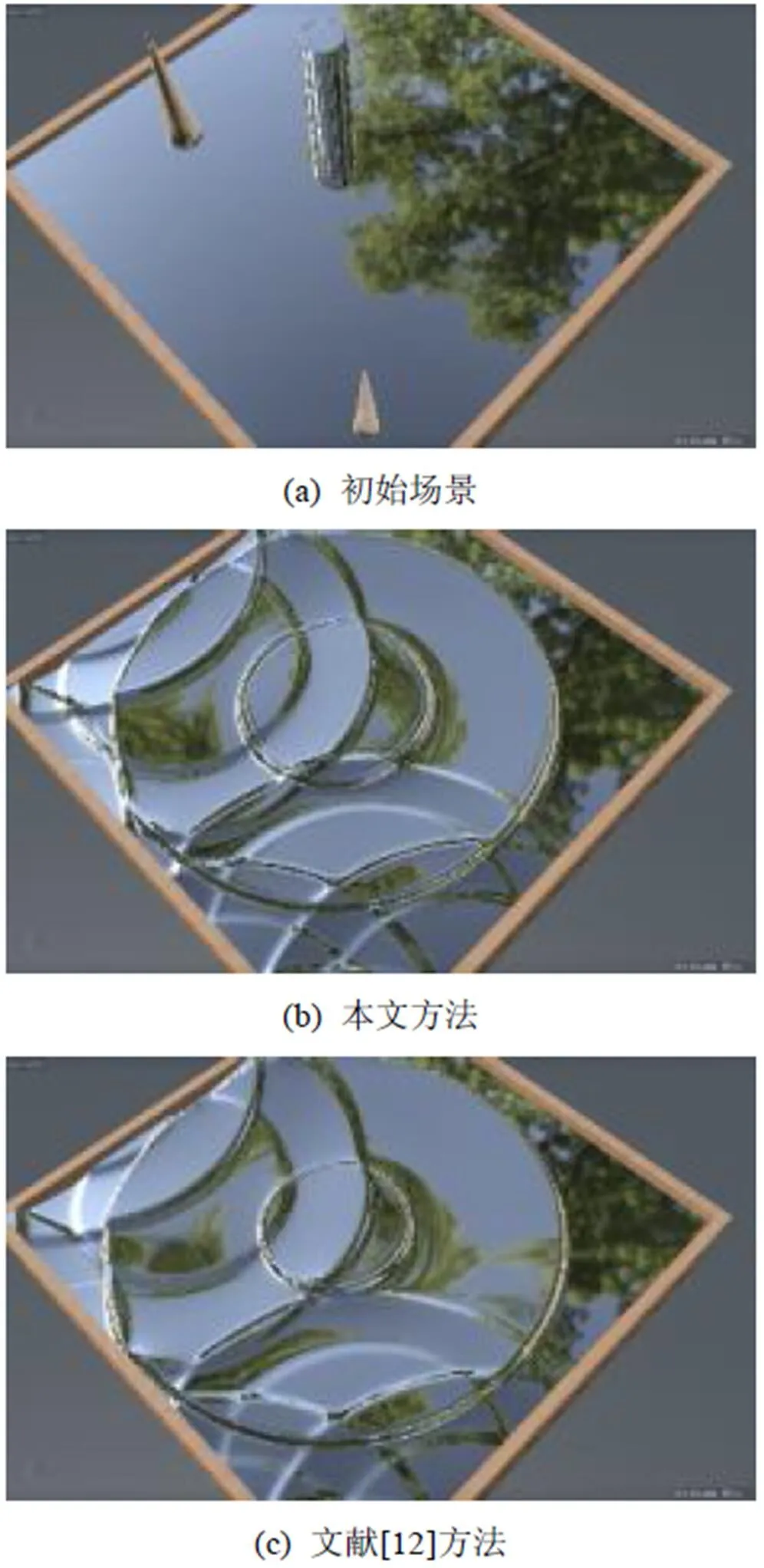
圖11 本文方法與文獻[12]方法的效果比較

進一步研究了本文算法的體積守恒特性。在不增加或去除水的情況下，通過對水深進行求和得出的總體積，在整個模擬過程中應該保持不變。在本文所有的實驗中，水的體積變化小于0.01%，由于變化極小，可認為實現了體積守恒。與文獻[9]的方法相比，如圖12所示，使用2種方法模擬圖7的場景，其效果基本相同。不過同樣是半拉格朗日隱式求解，如圖13所示，本文方法保證了體積守恒。

圖12 本文方法與文獻[9]方法的效果對比

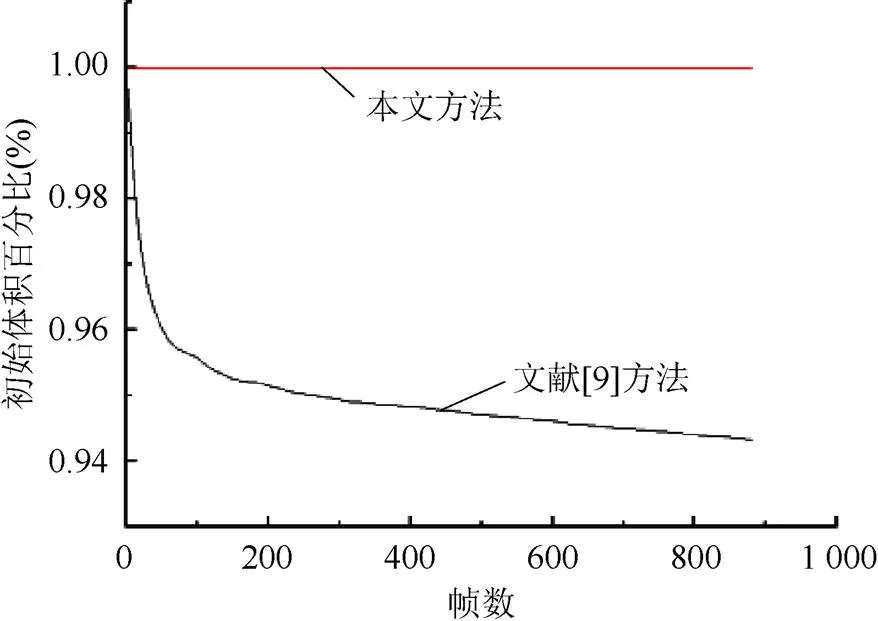
圖13 2種方法體積變化對比

4.3 進一步討論

到目前為止，通過本文方法已經實現了較大時間步長下的實時水體模擬，模擬過程中體積守恒，邊界處理令人滿意，單向流固耦合效果尚佳。但是水體模擬還有一些更有意思的事情，比如想要在水體的任意位置施加一個力、或者改變任意水體的速度。對于上述用戶指定的約束條件，本文方法可以實現。根據淺水方程來看，如果要給水體加上一定的約束條件，那么在每一步模擬的最后，改變水體的速度是最好的選擇。外力等其他條件，可以先將其轉化為動量通量，再轉化為速度的變化。通過該方法，可以更加靈活的模擬水體。圖14為本文方法模擬的風對水面的作用力[13]。

圖14 風對水面作用

5 結 論

本文提出了一個基于物理的水體模擬模型，該模型能夠模擬真實的水面，并且可以進行有效的單向流固耦合，即使在較大的時間步長下也能保持穩定，同時水體在模擬過程始終保持體積守恒。此外，因為基于淺水方程，所以效率很高，可以做到實時模擬。不過，模型的局限性也在于此，只能模擬淺水的無黏流動，對于更復雜的現象無法仿真。盡管如此，本模型在模擬溫和的海浪，對體積變化敏感的流體以及流固耦合方面還是可以起到很大的作用。下一步工作是實現雙向流固耦合，以及借助粒子的方法使得表面更富有細節且可以模擬一些破碎波浪等現象。

[1] JESCHKE S, WOJTAN C. Water wave animation via wavefrontparameter interpolation [J]. ACM Transactions on Graphics, 2015, 34(3): 1-14.

[2] 房克照, 尹晶, 孫家文, 等. 基于二維淺水方程的滑坡體興波數值模型[J]. 水科學進展, 2017, 28(1): 96-105.

[3] MICHEL-DANSACV, BERTHON C, CLAINS, et al. A well-balanced scheme for the shallow-water equations with topography or Manning friction [J]. Journal of Computational Physics, 2017, 335: 115-154.

[4] 張迪, 繆小平, 彭福勝, 等. 一種求解對流擴散方程的無條件穩定算法[J]. 水動力學研究與進展: A輯, 2017, 32(2): 158-164.

[5] ROBERT A. A semi-Lagrangian and semi-implicit numerical integration scheme for the primitive meteorological equations [J]. Journalof the Meteorological Society of Japan Ser II, 1982, 60(1): 319-325.

[6] LENTINEM, GRéTARSSON J T, FEDKIW R. An unconditionally stable fully conservative semi-Lagrangian method [J]. Journal of Computational Physics, 2011, 230(8): 2857-2879.

[7] LENTINE M, AANJANEYA M, FEDKIW R. Mass and momentum conservation for fluid simulation [C]// Proceedings of the 2011 ACM SIGGRAPH/ Eurographics Symposium on Computer Animation - SCA '11. New York: ACM Press, 2011: 91-100.

[8] LAYTON A T, LAYTON H E. A semi-Lagrangiansemi-implicit numerical method for models of the urine concentrating mechanism [J]. SIAM Journal on Scientific Computing, 2002, 23(5): 1526-1548.

[9] LAYTON A T, VAN DE PANNE M. A numerically efficient and stable algorithm for animating water waves [J]. The Visual Computer, 2002, 18(1): 41-53.

[10] HARLOW F H, WELCH J E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface [J]. Physics of Fluids, 1965, 8(12): 2182.

[11] QIAN S G, LI G, SHAO F J, et al. Positivity-preserving well-balanced discontinuous Galerkin methods for the shallow water flows in open channels [J]. Advances in Water Resources, 2018, 115: 172-184.

[12] CHENTANEZ N, MüLLER M. Real-time simulation of large bodies of water with small scale details [C]// Proceedings of the 2010 ACM SIGGRAPH/ Eurographics Symposium on Computer Animation.Goslar: Eurographics Association, 2010: 197-206.

[13] 鄒仲水, 趙棟梁, 黃健, 等. 海-氣界面動量通量的估計方法分析與應用[J]. 海洋學報:中文版, 2014, 36(9): 75-83.

Real-Time Simulation of Water with Volume Conservation in Large Time Step

ZHU Kui-xin1, GAI Meng2,3, LAI Shun-nan2

(1. Peking University Shenzhen Graduate School, Shenzhen Guangdong 518055, China; 2. School of Electronics Engineering and Computer Science, Peking University, Beijing 100871, China; 3. Beijing Engineering Technology Research Center of Virtual Simulation and Visualization, Peking University, Beijing 100871, China)

Physics-based fluid simulation can capture the movement of water. A common real-time simulation method is based on two-dimensional shallow water equation. Firstly, we introduce the two-dimensional shallow water equation, and then propose a new solution method, which is calculated by an implicit semi-Lagrangian method with volume conservation. This method allows a large time step while maintaining stability. Finally, we add additional correction steps to ensure volume conservation in the calculation process. In addition, a fluid solid coupling method based on momentum conservation is proposed, which works well. The model can simulate water more realistically in real time and ensure that the water volume is always conserved.

shallow water equation; semi-Lagrangian; volume conservation; large time step; fluid solid coupling

TP 391

10.11996/JG.j.2095-302X.2019040725

A

2095-302X(2019)04-0725-08

2019-03-26；

定稿日期：2019-04-26

國家重點研發計劃課題(2017YFB1002705)；國家自然基金面上項目(61872398，61632003)；裝備預研基金項目(315050501)

朱奎鑫(1997-)，男，河南商丘人，碩士研究生。主要研究方向為流體仿真。E-mail：zkx@pku.edu.cn

賴舜男(1965-)，女，重慶人，工程師，碩士。主要研究方向為虛擬仿真。E-mail：snlai@pku.edu.cn