高清彩色圖像分割的Mini-batch FCM算法研究

倪翠 李千 玄甲輝

摘? 要：模糊C-均值（Fuzzy C-Means，F(xiàn)CM）聚類算法是一種基于劃分的無監(jiān)督聚類算法，也是較為常見的圖像分割算法之一，該算法通過尋找0～1之間的模糊隸屬度等級來進行圖像分割，并通過在特征空間中尋找聚類中心來達到最小化目標函數(shù)的目的。它的局限性主要有實時性較差、初始聚類中心的設(shè)置對最終結(jié)果影響較大、未考慮空間因素導(dǎo)致抗噪性弱。本文將mini-batch方法應(yīng)用到FCM算法中，加快了FCM算法的收斂速度，提高了算法的效率及時效性，一定程度上解決了當(dāng)數(shù)據(jù)特征復(fù)雜、集合較大時，F(xiàn)CM算法的實時性不是很理想的問題，繼而節(jié)省算法運行的時間。

關(guān)鍵詞：FCM聚類;mini-batch;圖像分割

中圖分類號：TP391.41? ? ? 文獻標識碼：A 文章編號：2096-4706（2019）19-0015-03

Abstract：Fuzzy C-Means （FCM） clustering algorithm is an unsupervised clustering algorithm based on partition. It is also one of the common image segmentation algorithms. This algorithm conducts image segmentation by looking for the fuzzy membership grade between 0～1. The objective function is minimized by finding the clustering center in the feature space. Its limitations mainly include poor real-time performance，large impact on the final results due to the setting of the initial clustering center，and weak noise resistance due to the absence of space factors. In this paper，the mini-batch method is applied to the FCM algorithm to accelerate the convergence speed of the FCM algorithm，improve the efficiency and timeliness of the algorithm，and to some extent solve the problem that the real-time performance of the FCM algorithm is not ideal when the feature set of data is large，and then save the algorithm time.

Keywords：FCM clustering;mini-batch;image segmentation

1? FCM算法

1957年，Lloyd[1]首次提出了single-linkage層次聚類算法，經(jīng)典FCM算法是MacQueen[2]1967年提出的，對FCM算法的詳細分析和改進是由Dunn[3]和Bezdek[4]完成的。Bezdek等人對FCM進行了完善和推廣后，將FCM應(yīng)用在圖像分割方面。并且證明了該算法的收斂性[5]。

FCM是一種將樣本點進行分類的聚類算法，是K均值聚類算法的變體，也是最小化所有點到其聚類中心的距離之和，由于引進了介于0和1之間的隸屬度變量，將組合優(yōu)化問題變?yōu)檫B續(xù)變量優(yōu)化問題。

FCM模型的目標函數(shù)定義為：

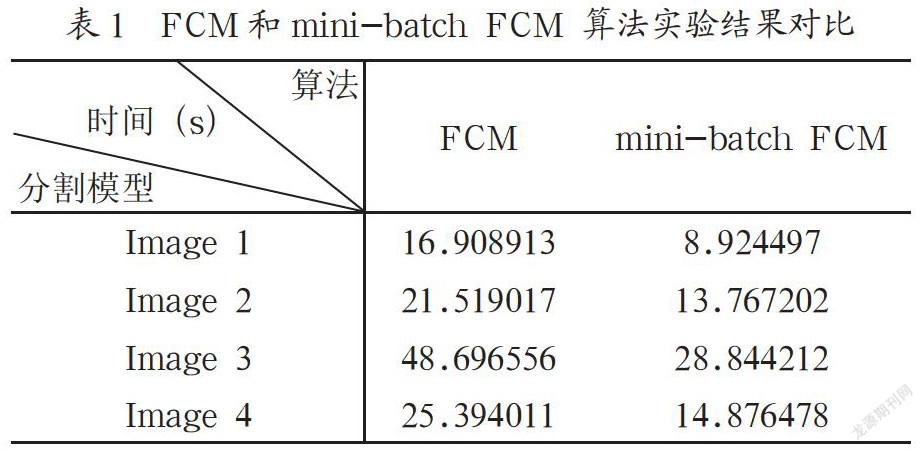
其中，U=（uik），1≤i≤C，1≤k≤m，為隸屬度矩陣，uik為k個樣本點屬于第i類的隸屬度，且，V=（vi），1≤i≤C，為樣本的聚類中心，1

目標函數(shù)值越小，像素點與其所屬聚類中心的隸屬度值越大;反之，目標函數(shù)值越大，像素點與其所屬聚類中心的隸屬度值越小。目標函數(shù)式（1）的最小化是通過不斷迭代更新隸屬度值uik，然后通過隸屬度值uik更新聚類中心vi來實現(xiàn)的。為了防止算法耗費過多的時間，F(xiàn)CM算法的終止準則為當(dāng)上一步的目標函數(shù)和本次的目標函數(shù)值之間的差小于某一個值時，算法停止，或者，當(dāng)算法的迭代步數(shù)達到了所給的最大迭代步數(shù)時，算法終止。在實際運用中，一般都是先達到第一種準則，即算法收斂。具體算法步驟如算法1（FCM算法）：

Step1 初始化：聚類類別數(shù)C，2≤C≤m，樣本個數(shù)m。迭代停止閾值ε，初始化隸屬度矩陣U，迭代計步器b=0;

Step2 用式（8）計算聚類中心vi，1≤i≤C;

Step3 用式（9）更新隸屬度值uik，1≤i≤C，1≤k≤m;

Step4 返回Step2繼續(xù)計算，b=b+1，直到收斂，輸出U=（uik），V=（vi）。

2? mini-batch FCM方法

傳統(tǒng)的FCM算法是用所有訓(xùn)練集更新隸屬度值uik和聚類中心vik，這樣大部分時間浪費在計算隸屬矩陣U和聚類中心V時的矩陣之間的運算上。為了能夠減少矩陣之間運算所消耗的時間。本文提出一種mini-batch FCM算法。mini-batch[6]通常和梯度下降法結(jié)合用來處理深度學(xué)習(xí)和機器學(xué)習(xí)中的大規(guī)模問題。mini-batch的思想是將訓(xùn)練集分組，分組之后，分別對每組進行計算，然后進行下一步迭代。假如將數(shù)據(jù)分為n組，則每次迭代將會做n次計算，這樣減少了大規(guī)模矩陣之間的運算時間，同時提升了收斂速度。

mini-batch FCM算法的思想為：為了讓每次計算的數(shù)據(jù)分布均勻，首先隨機打亂數(shù)據(jù)，然后將打亂后的數(shù)據(jù)分組，用每一組數(shù)據(jù)去更新隸屬度矩陣U和聚類中心V。這樣減少了隸屬矩陣U和聚類中心V在每次更新時所消耗的時間，同時使目標函數(shù)得到了充分的下降，提升了FCM的收斂速度。因此，mini-batch FCM算法比傳統(tǒng)的FCM省時。具體算法步驟如算法2（mini-batch FCM）：

Step1 給定m個樣本x1，…，xm，選取分組數(shù)n?m，一般有32、64、128等;

Step2 隨機分組：將m樣本隨機分成n組，前n-1組有[m/n]（向上取整）個樣本，第n組有m-[m/n]×（n-1）個樣本;

Step3 計算：用每一組樣本更新FCM算法中的隸屬度矩陣U和聚類中心V;

Step4 返回Step2繼續(xù)計算，直到收斂停止。

mini-batch FCM算法通過每次計算不同batch的樣本，能夠在一定程度上加速FCM算法收斂，使得達到相同精度，mini-batch FCM算法所用的時間更少，在相同的時間下，mini-batch FCM算法達到的精度更高。

3? mini-batch FCM實驗結(jié)果

在實驗中，取q=2，ε=10-8，C=2，mini-batch-size= 2048。圖1中的圖片采用高清彩色圖片。其中Image 1圖片的大小為473*1200*3。Image 2圖片的大小為1607*1600*3，Image 3圖片的大小為1600*1600*3，Image 4圖片的大小為1027*1600*3。

從表1可以看出傳統(tǒng)的FCM算法與mini-batch FCM算法相比，傳統(tǒng)FCM算法在處理圖像分割時所消耗的時間約是mini-batch FCM算法所消耗時間的2倍，尤其是處理尺寸大的高清彩色圖像時，效果更顯著。實驗表明，mini-batch FCM算法效率比傳統(tǒng)的FCM算法效率高。

4? 結(jié)? 論

在大數(shù)據(jù)時代，很多樣本的規(guī)模都很大，但是，當(dāng)數(shù)據(jù)的特征復(fù)雜、集合較大時，F(xiàn)CM算法的實時性不是很理想，于是，本文提出mini-batch FCM算法，在相同精度要求下，mini-batch FCM比FCM算法先收斂;在相同的時間下，mini-batch FCM的精度更高;因此，mini-batch FCM能夠加快FCM算法的收斂，同時避免了大型矩陣之間運算的耗時。

參考文獻：

[1] LLOYD S. Least squares quantization in PCM [J].IEEE Transactions on Information Theory，1982，28（2）：129-137.

[2] MACQUEEN J. Some methods for classification and analysis of multivariate observations [C]//Proc. of 5th Berkeley Symposium on Mathematical Statistics and Probability，USA：University of California Press，1967：281-297.

[3] DUNN J C. Well-Separated Clusters and Optimal Fuzzy Partitions [J].Journal of Cybernetics，2008，4（1）：95-104.

[4] BEZDEK J C. A convergence theorem for the fuzzy ISODATA clustering algorithm [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1980，2（1）：1-8.

[5] BEZDEK J C，EHRLICH R，F(xiàn)ULL W. FCM：The fuzzy c-means clustering algorithm [J].Computers & Geosciences，1984，10（2-3）：191-203.

[6] DEKEL O，GILAD-BACHRACH R，SHAMIR O，et al. Optimal Distributed Online Prediction using Mini-Batches [J].2012，13：165-202.

作者簡介：倪翠（1992-），女，漢族，寧夏中衛(wèi)人，助理工程師，碩士研究生，研究方向：機器學(xué)習(xí)中的優(yōu)化方法;李千（1970-），男，漢族，江蘇灌云人，副教授，碩士，研究方向：網(wǎng)絡(luò)大數(shù)據(jù)分析、嵌入式系統(tǒng)應(yīng)用;玄甲輝（1987-），男，漢族，山東泰安人，工程師，碩士研究生，研究方向：智能裝備系統(tǒng)與電子信息系統(tǒng)。