基于FRFT算法的移動平臺水聲信道編解碼技術研究
柴林峰 劉倩倩

摘 要:本文提出基于LFM-FRFT(線性調頻-分數階傅里葉變換)的聯合信道編解碼方式,在接收機端通過檢測LFM上下掃頻來解碼通信體制。LFM信號具有不敏感性,而FRFT通過分數階域能夠有效檢測LFM信號,達到解決多普勒引起的接收機信道不匹配問題。
關鍵詞:水聲通信;分數階傅里葉變換;LFM
中圖分類號:TN929.3 文獻標識碼:A 文章編號:1003-5168(2019)14-0008-04
Underwater Acoustic Channel of Mobile Platform
Based on FRFT Algorithm Research on Coding and Decoding Technology
CHAI Linfeng1,2 LIU Qianqian1,2
(1.The 27th Research Institute of China Electronic Technology Group Corporation,Zhengzhou Henan 450047;2.Zhengzhou Key Laboratory of Underwater Information System Technology,Zhengzhou Henan 450000)
Absratct: This paper proposed a joint channel coding and decoding method based on LFM-FRFT (Linear Frequency Modulation-Fractional Fourier Transform), which decoded the communication system by detecting LFM up-and-down sweep at at the receiver. Because of the Doppler insensitivity of LFM signal, FRFT can detect LFM signal effectively in fractional order domain to solve the channel mismatch problem caused by Doppler.
Keywords: underwater acoustic communication;;Fractional Fourier Transform;LFM
多普勒頻移對水聲通信系統產生了很大影響。長久以來,水聲通信領域工作者在對抗多普勒方面做出了很大努力,傳統的通信編碼較多采用PSK、FSK、OFDM、DSSS等方式。但是,在水聲信道中應用這些信道編碼方式存在較多問題,例如,PSK和FSK如果需要更遠的通信距離,則需要更大的瞬時功率,況且這兩種通信方式抗噪聲性能不佳;OFDM和DSSS雖然將信道能量拓展到一個帶寬內,降低了通信系統的瞬時功率,但是OFDM先天對多普勒具有敏感性,導致多普勒破壞子載波的正交性,引起接收機解碼困難;DSSS雖然通過接收機長時間累積,具有很強的抗干擾能力,但是對多普勒所引起的信號不相干問題,會導致累積增益優勢不明顯。因此,設計一種適合于水聲信道的高可靠性和多環境適應性的信道編碼方式顯得尤為急迫,一方面要參考無線電的編碼方式,但不能照搬;另一方面,要充分結合水聲信道的特點。本文運用Kebkal提出的掃頻-擴頻調制方式[1,2],結合掃頻信號的特點,改進接收機系統,采用LFM-FRFT的聯合信道編解碼方式快速完成信道解碼,適合工程化應用。
1 LFM信道編碼原理
線性調頻信號的構造方程為:
[yLFMt=A·expj2πf0t+πKt2+snK=BT-T2tT2] ? ? ? ? (1)
其中,[A]為信號增益;[f0]為線性調頻信號的中心頻率;[K]為調制斜率;[B]為調制帶寬;[T]為調制周期;[sn]為噪聲;fd為多普勒。
當[K>0]時,輸出的線性調頻信號稱為上掃頻,記為:[yLFM+t];當[K<0]時,輸出的線性調頻信號稱為下掃頻,記為[yLFM-t]。
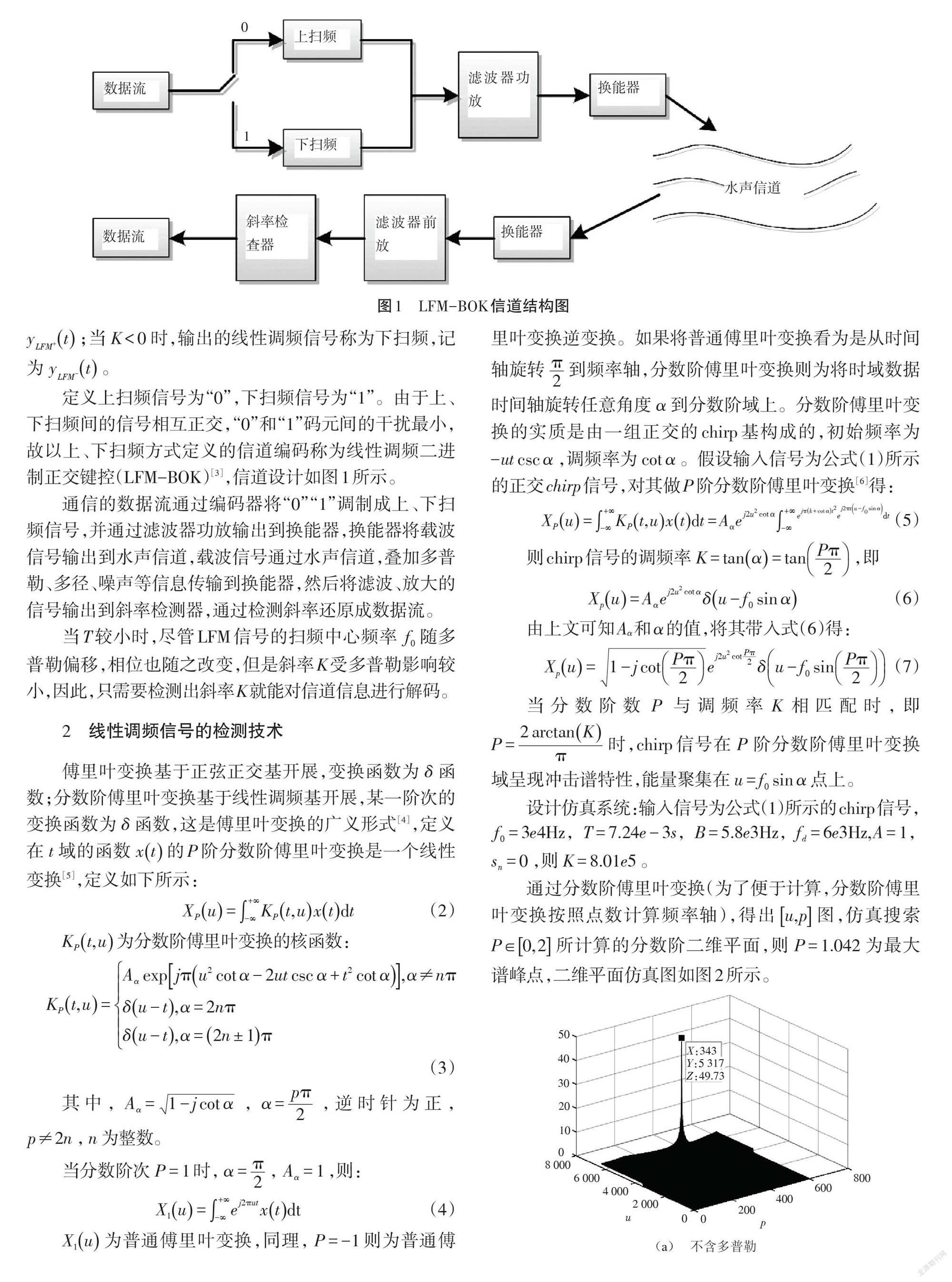
定義上掃頻信號為“0”,下掃頻信號為“1”。由于上、下掃頻間的信號相互正交,“0”和“1”碼元間的干擾最小,故以上、下掃頻方式定義的信道編碼稱為線性調頻二進制正交鍵控(LFM-BOK)[3],信道設計如圖1所示。
通信的數據流通過編碼器將“0”“1”調制成上、下掃頻信號,并通過濾波器功放輸出到換能器,換能器將載波信號輸出到水聲信道,載波信號通過水聲信道,疊加多普勒、多徑、噪聲等信息傳輸到換能器,然后將濾波、放大的信號輸出到斜率檢測器,通過檢測斜率還原成數據流。
當T較小時,盡管LFM信號的掃頻中心頻率[f0]隨多普勒偏移,相位也隨之改變,但是斜率K受多普勒影響較小,因此,只需要檢測出斜率K就能對信道信息進行解碼。
2 線性調頻信號的檢測技術
傅里葉變換基于正弦正交基開展,變換函數為[δ]函數;分數階傅里葉變換基于線性調頻基開展,某一階次的變換函數為[δ]函數,這是傅里葉變換的廣義形式[4],定義在[t]域的函數[xt]的P階分數階傅里葉變換是一個線性變換[5],定義如下所示:
[XPu=-∞+∞KPt,uxtdt] ? ? ? ? ? ? ? ?(2)
[KPt,u]為分數階傅里葉變換的核函數:
[KPt,u=Aαexpjπu2cotα-2utcscα+t2cotα,α≠nπδu-t,α=2nπδu-t,α=2n±1π](3)
其中,[Aα=1-jcotα],[α=pπ2],逆時針為正,[p≠2n],[n]為整數。
當分數階次[P=1]時,[α=π2],[Aα=1],則:
[X1u=-∞+∞ej2πutxtdt] ? ? ? ? ? ? ? ? ? ? ? ? ? ?(4)
[X1u]為普通傅里葉變換,同理,[P=-1]則為普通傅里葉變換逆變換。如果將普通傅里葉變換看為是從時間軸旋轉[π2]到頻率軸,分數階傅里葉變換則為將時域數據時間軸旋轉任意角度[α]到分數階域上。分數階傅里葉變換的實質是由一組正交的chirp基構成的,初始頻率為[-utcscα],調頻率為[cotα]。假設輸入信號為公式(1)所示的正交chirp信號,對其做P階分數階傅里葉變換[6]得:
[XPu=-∞+∞KPt,uxtdt=Aαej2u2cotα-∞+∞ejπk+cotαt2ej2πtu-f0sinαdt](5)
則chirp信號的調頻率[K=tanα=tanPπ2],即
[Xpu=Aαej2u2cotαδu-f0sinα] ? ? ? ? ? ? ? ? ? ? (6)
由上文可知Aα和α的值,將其帶入式(6)得:
[Xpu=1-jcotPπ2ej2u2cotPπ2δu-f0sinPπ2] (7)
當分數階數[P]與調頻率K相匹配時,即[P=2arctanKπ]時,chirp信號在[P]階分數階傅里葉變換域呈現沖擊譜特性,能量聚集在[u=f0sinα]點上。
設計仿真系統:輸入信號為公式(1)所示的chirp信號,[f0=3e4Hz,T=7.24e-3s,B=5.8e3Hz,fd=6e3Hz,A=1,][sn=0],則[K=8.01e5]。
通過分數階傅里葉變換(為了便于計算,分數階傅里葉變換按照點數計算頻率軸),得出[u,p]圖,仿真搜索[P∈0,2]所計算的分數階二維平面,則[P=1.042]為最大譜峰點,二維平面仿真圖如圖2所示。
<C:\Users\hnkj\Desktop\河南科技(創新驅動)2019年第14期_103928\Image\image47.png>[50][40][30][20][10][0][8 000][6 000][u][4 000][2 000][0][0][200][400][600][800][X:343][p][Y:5 317][Z:49.73]
(a) 不含多普勒
<C:\Users\hnkj\Desktop\河南科技(創新驅動)2019年第14期_103928\Image\image48.png>[50][40][30][20][10][0][8 000][6 000][4 000][2 000][u][0][0][200][400][600][800][p][X:343][Y:5 751][Z:48.09]
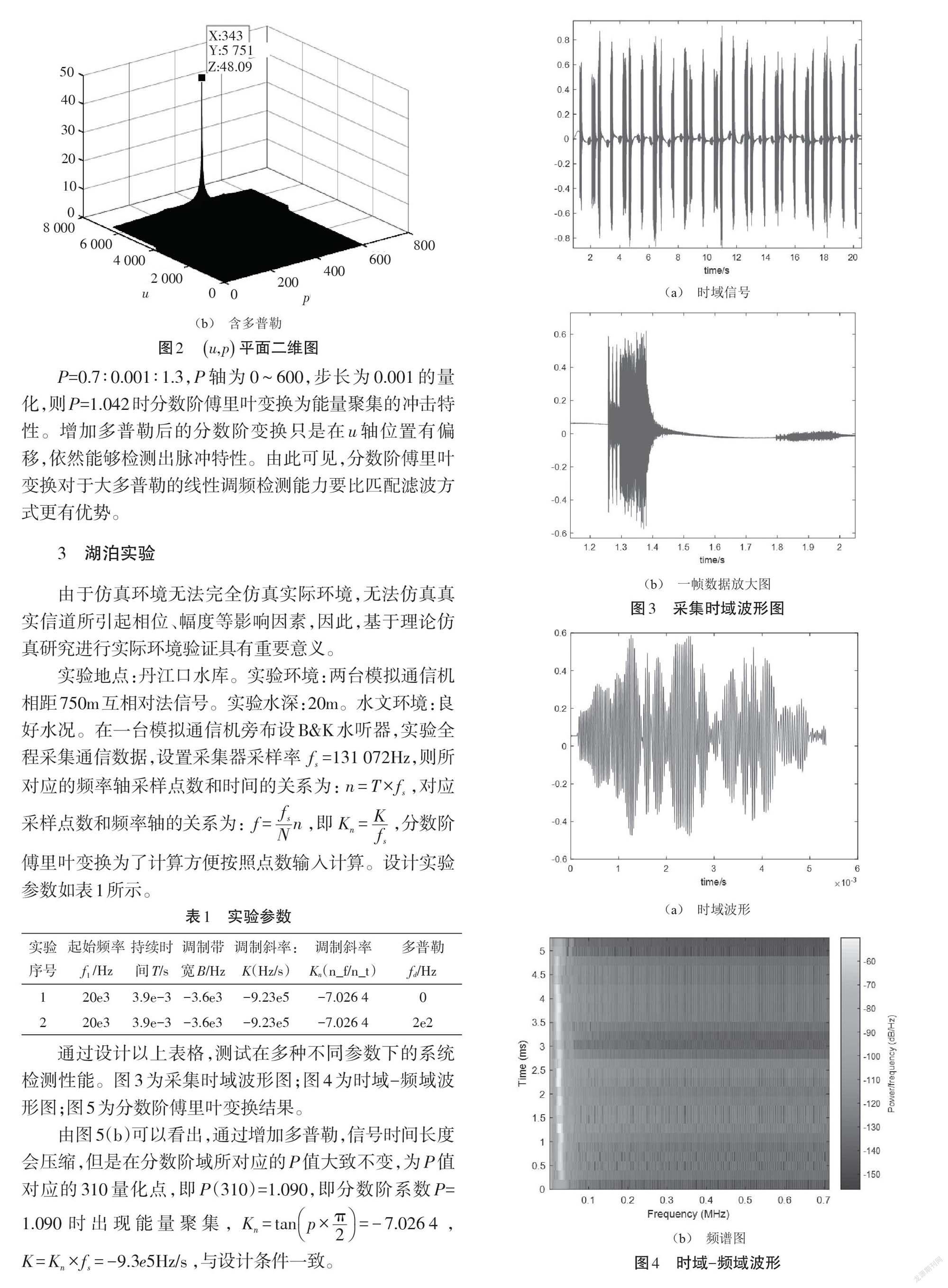
(b) 含多普勒
圖2 [u,p]平面二維圖
P=0.7∶0.001∶1.3,P軸為0~600,步長為0.001的量化,則P=1.042時分數階傅里葉變換為能量聚集的沖擊特性。增加多普勒后的分數階變換只是在u軸位置有偏移,依然能夠檢測出脈沖特性。由此可見,分數階傅里葉變換對于大多普勒的線性調頻檢測能力要比匹配濾波方式更有優勢。
3 湖泊實驗
由于仿真環境無法完全仿真實際環境,無法仿真真實信道所引起相位、幅度等影響因素,因此,基于理論仿真研究進行實際環境驗證具有重要意義。
實驗地點:丹江口水庫。實驗環境:兩臺模擬通信機相距750m互相對法信號。實驗水深:20m。水文環境:良好水況。在一臺模擬通信機旁布設B&;K水聽器,實驗全程采集通信數據,設置采集器采樣率[fs]=131 072Hz,則所對應的頻率軸采樣點數和時間的關系為:[n=T×fs],對應采樣點數和頻率軸的關系為:[f=fsNn],即[Kn=Kfs],分數階傅里葉變換為了計算方便按照點數輸入計算。設計實驗參數如表1所示。
表1 實驗參數
[實驗序號 起始頻率[f1]/Hz 持續時間T/s 調制帶寬B/Hz 調制斜率:
K(Hz/s) 調制斜率
Kn(n_f/n_t) 多普勒
fd/Hz 1 20e3 3.9e-3 -3.6e3 -9.23e5 -7.026 4 0 2 20e3 3.9e-3 -3.6e3 -9.23e5 -7.026 4 2e2 ]
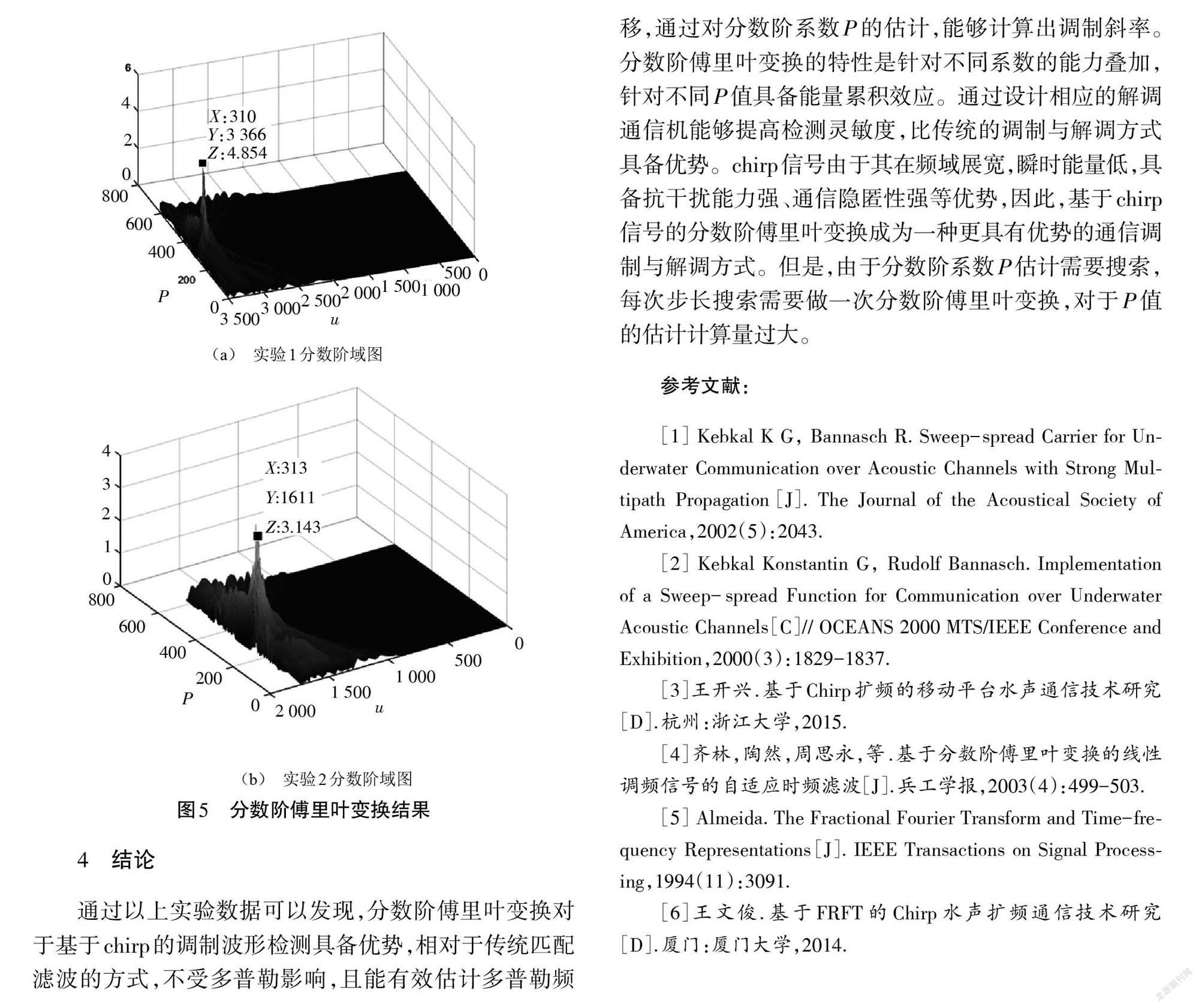
通過設計以上表格,測試在多種不同參數下的系統檢測性能。圖3為采集時域波形圖;圖4為時域-頻域波形圖;圖5為分數階傅里葉變換結果。
由圖5(b)可以看出,通過增加多普勒,信號時間長度會壓縮,但是在分數階域所對應的P值大致不變,為P值對應的310量化點,即P(310)=1.090,即分數階系數P=1.090時出現能量聚集,[Kn=tanp×π2=-7.026 4],[K=Kn×fs=-9.3e5Hz/s],與設計條件一致。
(a) 時域信號
(b) 一幀數據放大圖
(a) 時域波形
(b) 頻譜圖
(a) 實驗1分數階域圖
4 結論
通過以上實驗數據可以發現,分數階傅里葉變換對于基于chirp的調制波形檢測具備優勢,相對于傳統匹配濾波的方式,不受多普勒影響,且能有效估計多普勒頻移,通過對分數階系數P的估計,能夠計算出調制斜率。分數階傅里葉變換的特性是針對不同系數的能力疊加,針對不同P值具備能量累積效應。通過設計相應的解調通信機能夠提高檢測靈敏度,比傳統的調制與解調方式具備優勢。chirp信號由于其在頻域展寬,瞬時能量低,具備抗干擾能力強、通信隱匿性強等優勢,因此,基于chirp信號的分數階傅里葉變換成為一種更具有優勢的通信調制與解調方式。但是,由于分數階系數P估計需要搜索,每次步長搜索需要做一次分數階傅里葉變換,對于P值的估計計算量過大。
參考文獻:
[1] Kebkal K G, Bannasch R. Sweep-spread Carrier for Underwater Communication over Acoustic Channels with Strong Multipath Propagation[J]. The Journal of the Acoustical Society of America,2002(5):2043.
[2] Kebkal Konstantin G, Rudolf Bannasch. Implementation of a Sweep-spread Function for Communication over Underwater Acoustic Channels[C]// OCEANS 2000 MTS/IEEE Conference and Exhibition,2000(3):1829-1837.
[3]王開興.基于Chirp擴頻的移動平臺水聲通信技術研究[D].杭州:浙江大學,2015.
[4]齊林,陶然,周思永,等.基于分數階傅里葉變換的線性調頻信號的自適應時頻濾波[J].兵工學報,2003(4):499-503.
[5] Almeida. The Fractional Fourier Transform and Time-frequency Representations[J]. IEEE Transactions on Signal Processing,1994(11):3091.
[6]王文俊.基于FRFT的Chirp水聲擴頻通信技術研究[D].廈門:廈門大學,2014.

