巧用電子書包,提高初中數學教學效率
李富強
摘要:二十一世紀,人類社會已進入信息化時代,信息化教學得到廣泛應用,形成一種以現代信息技術為基礎的現代教學模式。而“電子書包”是信息化教育改革的產物,是信息技術與教育深度結合的一種電子產品。本文針對“電子書包”在初中數學教學中的應用方法開展探討,旨在提高初中數學教學效率。
關鍵詞:電子書包?初中數學?數學教學?教學效率
數學是初中教學體系中的基礎學科,電子書包的興起和應用推動了數學課堂的信息化、數字化,為教師和學生提供了高效的學習交流平臺,可以有效促進學生的個性化發展。因此,初中數學教師應該充分重視電子書包,有效發揮其教學作用,將電子書包引入數學課堂。電子書包實質上就如同普通書包一樣,學生打開電子書包就可以隨時翻閱電子課本,學習知識,主要區別在于電子書包使用起來更加輕便、知識容量更大、更新更快。如果教師能夠巧妙應用電子書包,就可以有效引導學生開展高效數學學習,可見,探討電子書包的應用策略有助于提高初中數學教學效率,促進學生數學綜合素養的提升。
一、創設情境引導學生自主學習
在初中數學教學實踐中,如果教師機械地向學生灌輸知識,學生就無法體會到學習的樂趣,久而久之就喪失了學習數學的興趣。為了解決這個問題,教師要善于結合教學內容創設各種各樣的教學情境激發學生學習熱情。而電子書包具備豐富的多媒體功能,教師可以借助電子書包的多媒體功能為學生創設生動的教學情境,促使學生主動學習數學。例如,在教學立體幾何圖形的相關知識時,教師可以讓學生用電子書包連接事先制作好的多媒體教學課件,讓學生自主選擇學習內容。利用電子書包播放多媒體課件為學生直觀呈現長方體、正方體、圓柱體、圓錐體等圖形,利用生動的動畫視頻全方位展現立體幾何圖形的形狀、特點,以激發學生的學習興趣,再引導他們回答問題:立體幾何圖形的構成方式是怎樣的?如果學生回答錯誤就可以重新瀏覽多媒體課件尋找正確答案。學生在觀看動畫視頻,回答基礎性問題的過程中將逐漸掌握這節課需要學習的基礎知識,為后續的課堂學習做好鋪墊,同時學生在愉快的氛圍中學習數學,有助于提高學習效率。
二、用電子書包引導學生合作探究
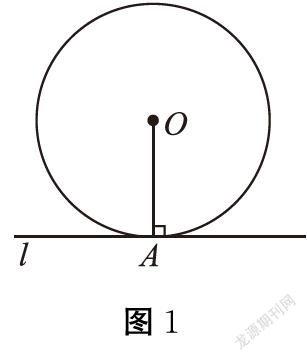
在引導學生開展自主學習的基礎上,初中數學教師可以利用電子書包給學生推送教學資料,通過相應的教學活動組織學生圍繞數學問題開展圖1合作探究。例如,在教學“點、直線、圓和圓的位置關系”時,教師可以先創設問題情境:一個圓,圓心為O,半徑OA,直線 經過圓O的半徑OA外端點A,且與半徑OA垂直,請問符合上述條件的直線由幾條?它們和圓O有幾個交點?然后將學生分為多個學習小組,以小組為單位利用電子書包中的幾何軟件,通過小組合作畫出圖形,展示小組討論成果。如圖1所示。
學生自己動手發現問題,解決問題,在與其他同學的合作交流中經歷從自主發現到合作探究的過程,從而對知識獲得更深的認識,進一步深化自己的數學知識結構,實現學以致用。這時教師再引導學生在電子書包中移動半徑OA在圓上的點A,讓學生發現經過點A同時與半徑垂直的直線也會隨著半徑轉動,然后教師在給學生演示動畫,使學生形成直觀感知,在此基礎上提問學生:固定半徑有幾條垂線?經過點A同時與半徑垂直的直線一定是圓的切線嗎?要求學生進行分組討論,然后選派代表陳述本組的討論結果。最后由教師對切線的概念進行總結:“經過半徑的外端且與半徑垂直的直線是圓的切線。”同時強調根據切線定義可知經過圓上一點的切線只有一條。這樣一來,學生就能更加清晰地認知切線地概念和定義。
在學生掌握切線概念定義地基礎上,教師可以利用電子書包開展教學活動,引導學生理解和掌握切線性質。首先提問學生:假如直線 是圓的切線,點A為切點,則半徑OA是否與直線 垂直?要求學生以小組為單位圍繞問題進行交流討論,然后選派代表陳述觀點,回答問題。再由教師進行點評總結:因為直線 是圓的切線,圓心O到直線 的距離與半徑長度相等,OA是圓心O到直線 的距離,可知半徑OA與直線 垂直,從而導出切線性質:圓的切線與經過切點的半徑垂直。使學生明白切線判定和切線性質是識別切線的兩種方式,方式不同但本質相同。在解決具體問題時,需要結合問題條件選擇適當方法。在判定切線時,要明確兩個特點:第一,直線經過半徑外端,第二,直線與半徑垂直,引導學生反面運用所學知識,加深學生理解,同時培養其逆向思維能力。
在學生掌握了切線性質及判定方法后,教師可以利用電子書包開展教學活動,引導學生理解并應用切線長定義。先創設問題情境:經過圓上某點作圓切線只能作一條,那么經過圓外某點能做幾條圓切線?然后組織學生利用電子書包中的幾何軟件動手畫圖,圍繞圖形開展小組討論,得出結論:經過圓外一點可以作兩條圓切線。在此基礎上引導學生探究兩條切線之間的關系以及該點與圓心連線分別與切線構成的兩個夾角之間的關系。學生通過小組合作探究獲得結論:兩條切線長度相等,點和圓心連線平分切線夾角。這時教師要向學生強調切線是不限長度的直線,但為了方便研究切線性質就需要定義切線長度,讓學生注意切線長的定義方法。在這個探究活動中,學生通過動手畫圖,觀察圖形得出切線長度相等的結論,通過畫輔助線構造全等三角形,證明圓外一點與圓心連線平分兩條切線的夾角,從而理解切線長定義。
最后,教師可以利用電子書包組織學生合作探究三角形的內切圓、內心和圓的外切三角形等概念。首先給學生展示一個三角形,然后在三角形上截取一個圓,提問學生:如何截取才能獲得最大面積的圓?引導學生進行小組討論,展示討論成果。以此鍛煉學生的知識運用能力和總結歸納能力。教師可以在此問題的基礎上進一步深化,引導學生結合三角形和切線性質,得到三角形的內切圓。課堂是培養學生思維的重要平臺,學生通過實際動手、動腦發現知識,在教師的指導下加深理解,并能夠鍛煉應用,在探索的過程中結合以前的知識進行探究,從而加強知識的關聯。
三、利用電子書包加深知識理解
初中數學教材中的練習主要針對基礎知識,比較簡單,學生單靠課本練習很難真正理解知識。因此,教師應該利用電子書包組織學生開展強化練習,加深學生對知識的理解,同時提高學生運用知識解決實際問題的能力。題目①假設直線AB經過圓O上的一點A,已知AB=OA ,∠OBA=45°,請問直線AB是圓切線嗎?為什么?要求學生利用電子書包自行完成該題目,教師需全程關注學生的練習情況,當學生遇到困難時要給予及時的幫助。然后再提問學生:如果圓心O在∠BAC的邊AC上,邊BC與圓相切于點D,OB平分∠ABC,請證明三角形的邊AB與圓相切。教師可以引導學生運用切線性質作輔助線連接OD,得OD與BC垂直,但是AB與圓是否存在公共點,根據題目條件無法確定,這時教師可以引導學生結合題目①進行比較分析,得出作輔助線的方法:作OE⊥AB于E,根據角平分線的條件可知OD = OE,從而證明AB與圓相切。教師可以將這兩個題目作為隨堂練習加以講解,以提高學生分析問題的能力,加深知識理解。
參考文獻:
[1]陳志剛. 巧妙應用電子書包工具,提高初中數學教學效率[J]. 中學生數理化(高考數學), 2014(5).
[2]李強. 初中數學教學中“電子書包”應用分析[J]. 教育:文摘版:0014900149.
[3]商慶平. 利用電子書包提高中學數學教學的有效性[J]. 教育信息技術, 2013(3):3841.
責任編輯:裴?帔

