“旋轉體的概念”：基于相似性，重構數學史

張益明 李卓忱

摘要：在梳理《幾何原本》《九章算術》中的旋轉體概念、問題以及西方早期幾何教科書中的圓柱概念的基礎上，采用HPM視角來設計“旋轉體的概念”的教學：首先，欣賞歷史上著名的圓柱形建筑或物體，思考圓柱形的好處，感悟學習旋轉體的必要性;接著，利用一個圓形紙片、一張長方形的紙片、兩支筆等工具，通過圖形的旋轉和平移形成圓柱，并利用數學語言逐步完善圓柱的概念;最后，利用類比思想形成圓錐、球的概念，并概括出一般旋轉體的概念，進一步思考旋轉體的集合定義。

關鍵詞：HPM旋轉體概念圓柱定義

立體幾何研究現實世界中物體的形狀、大小與位置關系。《普通高中數學課程標準（2017年版）》要求“利用實物、計算機軟件等觀察空間圖形，認識柱、錐、臺、球及簡單組合體的結構特征，能運用這些特征描述現實生活中簡單物體的結構”。滬教版高中數學三年級第15章《簡單幾何體》第3節的內容是“旋轉體的概念”。教材在本節開頭部分開門見山地給出了旋轉體的概念，接下來依次給出了圓柱、圓錐以及球的概念。學生經過《空間直線與平面》一章的學習，需要在這一章的學習中進一步發展空間想象能力。教師需要用動態的觀點進行教學，突出概念的本質特征，強調概念的精確性和簡練性。

在實際教學中，教師往往覺得本章內容枯燥無趣，因而重視不夠，相關教學研究也比較少。經過多年教學，筆者發現，按照直接引入的方式，學生也能掌握圓柱、圓錐以及球的概念，而且能夠節省時間來進行練習。但是，這種引入方式存在以下幾點缺陷：學生不理解學習旋轉體的必要性;沒有獲得通過圖形的運動形成幾何體的觀念;對定義的嚴密性理解不夠深刻。

HPM視角下的教學實踐表明，數學史有助于構建知識之諧、彰顯方法之美、營造探究之樂、實現能力之助、展示文化之魅、達成德育之效。歷史上，人們對旋轉體的概念經歷了逐漸完善的過程。基于歷史重構旋轉體概念的教學，有助于激發學生學習旋轉體概念的動機，讓學生經歷旋轉體概念的形成過程，了解知識的源流，加深對概念的理解，同時培養學生的空間想象能力和動態發展的數學觀。

有鑒于此，我們采用HPM視角來設計本節課的教學，擬定了如下教學目標：（1）知道旋轉體的有關概念;（2）經歷圓柱、圓錐、球概念的形成，理解三個旋轉體的基本性質;（3）進一步培養類比思想、空間想象能力。

一、歷史材料梳理

（一）《幾何原本》中的旋轉體概念

古希臘數學家歐幾里得（Euclid，公元前3世紀）在《幾何原本》第11卷中分別給出了球、圓錐、圓柱的動態定義：“固定半圓的直徑，旋轉半圓到開始的位置所形成的圖形稱為球。”“固定直角三角形的一條直角邊，旋轉直角三角形到開始的位置所形成的圖形稱為圓錐。”“固定矩形的一邊，繞此邊旋轉矩形到開始的位置所成的圖形稱為圓柱。”

之后，古希臘數學家海倫（Heron，1世紀）給出了球的靜態定義：“一個被表面包圍的立體圖形，所有從里面一點出發的直線都與另一條相等。”

可以看出，此時關于旋轉體的概念已經有動態和靜態的雛形。

（二）《九章算術》中的旋轉體問題

中國古代數學典籍《九章算術》（1世紀）記載了有關圓柱（古人稱之為圓堡壔）、圓錐和球（古人稱之為立圓）的實際應用問題。比如關于圓柱的一題：“今有圓堡壔，周四丈八尺，高一丈一尺，問積幾何。答曰：兩千一百一十二尺。術曰：周自相乘，以高乘之，十二而一。”此時，中國古代數學家關注的是旋轉體的度量與實際應用。

（三）西方早期幾何教科書中的圓柱概念

通過對西方早期教科書的考察，可以得到圓柱的五種定義方式，分別是矩形旋轉定義、直線旋轉定義、圓的平移定義、基于圓柱面的定義、基于圓柱空間的定義。

1829年，英國數學家海華德（J.Hayward，1786—1866）在《幾何學基礎》中將圓柱定義為“矩形繞其一邊旋轉所形成的立體”。這與《幾何原本》中的定義一致。他在書中還給出了圓柱另外兩種動態定義：一是“過圓上一點的直線沿著圓平移所形成的立體”，二是“圓沿著一條直線平移所形成的立體”。

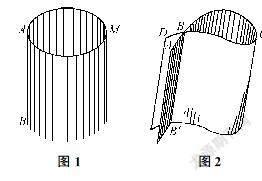
1884年，美國數學家紐康姆（S.Newcomb，1835—1909）在《幾何學基礎》中首先定義了圓柱面：“圓柱面是由直線的運動產生的，該直線始終與給定的曲線相交，并且與其原始位置保持平行（如圖1）。”然后定義了圓柱：“由一個圓柱面和兩個平行平面構成的幾何體為圓柱。”由于曲線的任意性，這里定義的是廣義的圓柱。1893年，美國數學家巴托爾（W.C.Bartol）在這個定義的基礎上，特別強調了“底為圓、母線與底面垂直的幾何體是直圓柱”。這與圓柱的現代定義是一致的。他還指出，直圓柱也稱為旋轉圓柱：“矩形繞其一邊旋轉，產生一個直圓柱。”該旋轉定義

與圓柱的現代動態定義是一致的。

1900年，Beman等人首先定義了柱面空間：“如果準線是一條閉合曲線，柱面就包圍了一個無限長空間，稱為柱面空間（如上頁圖2）。”據此給出了柱體的定義：“柱面空間中，含于兩個平行橫截面之間的部分稱為柱體。”由此，若準線垂直于底面，則柱體是直柱體;如果一個柱體的底是一個圓，那么這個柱體就是圓柱。

二、教學設計與實施

考慮到學生的認知基礎以及本節課的教學目標，我們對圓柱概念的歷史進行了重構：首先，穿越時空，欣賞歷史上著名的圓柱形建筑或物體，思考圓柱形的好處，感悟學習旋轉體的必要性;接著，重演歷史，利用一個圓形紙片、一張長方形的紙片、兩支筆等工具，通過圖形的旋轉和平移形成圓柱，并利用數學語言逐步完善圓柱的概念;最后，反思歷史，利用類比思想形成圓錐、球的概念，并概括出一般旋轉體的概念，進一步思考旋轉體的集合定義。

（一）情境引入，再識圓柱

教師指出：“國慶期間，各大旅游網站，都會推薦相應的景點。1916年，韋伯在其教科書《立體幾何》中也介紹了一個景點，即梅特拉墓。”同時，出示梅特拉墓圖，并介紹：“這個墓地是古羅馬貴婦人的墓地，是世界十大女性遺跡之一，意大利著名景點。”然后，出示歐洲古代水塔圖，并介紹：“這是歐洲古代的水塔。”接著，提問：“這兩個建筑都是什么形狀的幾何體？”

學生回答之后，教師出示中國古代的圓柱形物體，如故宮的柱子、西漢的搟面杖、古代的水井等，并讓學生討論圓柱形有哪些優點。學生從美觀、安全、存儲量等角度給出了優點，體會到學習圓柱的必要性。

（二）再現歷史，定義圓柱

（教師引導學生回憶圓的軌跡定義和集合定義，并比較。）

師我更喜歡軌跡說。軌跡說的核心是點在運動，更加動感、活潑，也更有探索和創新精神。這個時候，點不再是冷冰冰的概念，而是富有活力的生命體，因為生命在于運動。（稍停）現在，請同學們利用老師提供的材料——圓紙片、A4紙、筆等，通過圖形的運動形成圓柱。

生圓向上平移，筆繞著圓旋轉一周，旋轉A4紙。

生將A4紙卷成圓柱。

師卷的過程中紙的邊可以看成直線，因此，它與筆旋轉的方案等價。這里的筆在數學家眼中不再是筆，而是直線。請同學們用數學語言將剛才的方案描述出來，得到圓柱的定義。

生將一條直線繞著圓周旋轉一周得到的幾何圖形。

師很好，這種定義已經和歷史上數學家的定義相近了。1829年，英國數學家海華德在《幾何學基礎》中給出了圓柱的三種定義。其中，直線旋轉定義為，空間中經過圓上一點的一條直線沿著圓平移，形成圓柱的表面。同學們覺得這種定義準確嗎？

生直線是無限延伸的，沒有界限，因此，得到的不是封閉的幾何體。

師那么，如何修正這個定義？

生上下加兩個蓋子。

師意思差不多，圓柱其實就是被圓柱面和兩個平行平面包圍的立體。1884年，美國數學家紐康姆在《幾何學基礎》中基于直線旋轉定義給出了一種新的圓柱定義——基于圓柱面的定義：首先定義圓柱面為空間中一條直線沿著一條曲線平移形成的面，接著定義圓柱為被一個圓柱面和兩個平行平面包圍的立體。解決了封閉性的問題之后，由現在這個定義得到的圓柱和我們黑板上的圓柱一樣嗎？

生不一定一樣，可以是斜的。

師請舉出一個著名旅游景點的例子。

生比薩斜塔。

師很好！1893年，美國數學家巴托爾在基于圓柱面的定義的基礎上，給出了更完善的圓柱定義：“如果底是圓形，生成柱面的直線垂直于圓所在平面，這個柱體就被稱為直圓柱。”這里的“直圓柱”就是現在的圓柱。（稍停）剛才，我們一起利用直線旋轉形成了圓柱。在圓柱定義不斷完善的過程中，數學家們在追求真知的道路上不斷探索的精神以及嚴謹求實的態度非常值得學習。同學們也能和數學家一樣提出相似的定義，說明大家在數學學習上是非常有潛力的。現在，請同學們類似地利用圓的平移給出圓柱的定義。

生一個圓沿著一條直線平移，形成圓柱面，而且這條直線與圓面垂直，上下要加蓋子。

師不錯，意思基本對了。海華德在《幾何基礎》中還給出了一種矩形旋轉定義：矩形繞其一邊旋轉所形成的立體。而《幾何原本》第11卷也給出了類似的定義。請同學們點評上述三種定義：直線旋轉定義（包括其改進版）、圓的平移定義以及矩形旋轉定義，你更喜歡哪一種？為什么？

生圓的平移定義，因為它最簡潔。

生直線旋轉定義，因為有一種動態。

生矩形旋轉定義，因為旋轉的矩形中外面那條邊也可以看作直線，從而把直線旋轉包含進去，也把封閉性和垂直性包含進去。

師因此，課本上還是用了矩形旋轉定義：將矩形ABCD（及其內部）繞其一條邊AB所在直線旋轉一周，所形成的幾何體叫作圓柱。這個定義非常嚴謹，比如強調了矩形及其內部;非常動感，利用了圖形運動形成圓柱;也很簡潔，旋轉一周就行了。

（教師帶領學生學習圓柱中軸、母線、高、底面等定義。）

（三）類比研究，深入理解

師我們經歷過一個圖形、兩種運動、三種定義。請同學們基于圓柱的旋轉定義類比給出圓錐和球的旋轉定義。

生圓錐的定義為將Rt△ABC（及其內部）繞其一條直角邊AB所在直線旋轉一周所形成的幾何體。

生球的定義為將圓心為O的半圓（及其內部）繞其直徑AB所在直線旋轉一周所形成的幾何體。

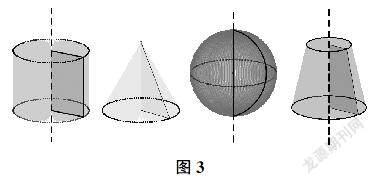
師我們利用不同的圖形，比如矩形及其內部、直角三角形及其內部、半圓及其內部，繞著直線旋轉一周得到相應的幾何體。那么，我們拿出其他幾何圖形，是不是也能夠得到相應的旋轉體呢？（稍停）平面上一條封閉曲線所圍成的區域繞著它所在平面上的一條定直線旋轉而形成的幾何體。（利用幾何畫板動畫展示圓柱、圓錐、球、圓臺的形成過程，如圖3）現在，請同學們舉出生活中的旋轉體例子。

生冰激凌、車的方向盤、輪胎。

（一位學生展示旋轉舞蹈。）

師不同的造型旋轉起來非常優美。請同學們思考一下：為什么今天所學的旋轉體的名稱中都有一個“圓”字。

生動點繞定點旋轉會形成圓。

（四）練習鞏固，深化認識

教師給出一些例子，讓學生辨析，從而強化之前學習的概念。

例題下列說法正確的是。

（1）以矩形的一邊所在直線為旋轉軸，其余三邊旋轉一周形成的曲面所圍成的幾何體是圓柱;

（2）以直角三角形的一邊所在直線為旋轉軸，其余兩邊旋轉一周形成的曲面所圍成的幾何體是圓錐;

（3）在圓柱上、下底面的圓周上各取一點，這兩點的連線是圓柱的母線;

（4）圓錐的頂點和底面的圓周上一點的連線是圓錐的母線;

（5）將半圓繞其直徑所在直線旋轉一周所形成的幾何體是球;

（6）空間中到定點的距離等于定長（大于0）的點構成的集合是球。

（五）探索創新，回顧總結

師下面也請同學們用嚴謹的態度，創新性地探索圓柱的集合定義。

生到定直線l距離等于定值且與l平行的直線構成的集合記為Ω，垂直于定直線l的兩個平行平面與Ω包圍的幾何體稱為圓柱。

生過定直線上一點且與定直線所成角相等的直線構成的集合記為Ω;垂直于定直線且不過該定點的平面與Ω包圍的幾何體稱為圓錐。

生空間中，到定點的距離小于等于定長的點構成的集合稱為球。

最后，師生共同總結本節課的數學知識，即圓柱、圓錐、球以及旋轉體的概念，總結本節課的數學思想方法，即類比的思想和運動的觀點;引導學生學會用數學的眼光觀察世界，用數學思維思考世界，用數學語言表達世界，即善于觀察生活問題，進行數學抽象，并形成數學問題，再加以解決。

三、學生反饋

課后，我們收集了全班40名學生對于本節課的反饋信息。

96%的學生“非常同意”聽懂了這節課的教學內容。98%的學生“很喜歡”這樣將歷史上的旋轉體概念融入課堂中。

當看到“旋轉體”這個詞時，38%的學生會想到旋轉體與其中的元素;12%的學生會想到運動及其他數學相關詞匯;8%的學生會想到圖形性質與審美;6%的學生會想到跨學科內容;30%的學生會想到旋轉體與生活。

對于為什么要學習旋轉體，在數學知識與技能方面，有27人分別從數學史、低維到高維、圖形的對稱、學習知識、定義、理解立體幾何、空間想象力等知識取向的角度進行了闡述;5人從數學定義的方法、數學語言的角度進行了解釋;10人從數學思維的角度進行了詮釋。在數學與生活方面，有16人從研究數學、生活、世界的角度進行了解釋。在數學情感方面，有4人從情感取向解釋了學習旋轉體時追尋真理、深入本質的研究態度以及反復研究和改進結論帶來的數學之美、好玩的情感。由此可以看出，學生對學習旋轉體概念的必要性有了一定的認識。

對于如何定義圓臺，35人利用直角梯形及其內部的旋轉;1人利用線段繞軸的旋轉;1人利用錐體截取上方小的圓柱;1人利用兩個大小不等、圓心連線與圓所在平面垂直的平行圓，聯結圓上對應點所形成的幾何體及其內部;1人利用集合論，即圓柱側面與上下圓心連線夾角相同的直線。由此可以看出，學生初步形成了幾何運動觀念，并且對定義的嚴密性有了一定的理解。

對于學完本節課后印象深刻的有哪些，學生的典型回答有：“歷史上的概念。因為感覺數學家提出這個概念時間很近，而且他們思考得并不全面，讓我驚奇。”“了解發現的歷史演變過程。因為了解到揭示規律、真理是在不斷改進之后產生的。”“同一圓柱的不同定義。因為數學有時也沒有唯一的規定。”“由古至今，分析定義。因為數學定義并非一下子得出的，而是經過不斷地修改與加工，才得以完善。”由此可以看出，學生初步形成了動態發展的數學觀。

四、教學反思

本節課HPM的使用方式有順應式、重構式和附加式。在情境引入中用順應式，介紹韋伯在《立體幾何》中呈現的梅特拉墓以及歐洲古代水塔，旨在幫助學生提升數學學習興趣，感悟數學來源于生活。在圓柱概念的形成中用重構式，讓學生利用所給材料，通過圖形運動形成圓柱，并根據設計的方案，利用數學語言表達圓柱定義;在學生不斷完善定義和辨析定義優缺點的過程中，自然地引入相應的數學史上的定義。課后應用附加式，讓學生自主閱讀圓錐概念的歷史發展過程。

本節課中，學生自己設計構成圓柱的方案，并抽象成數學概念，對比數學史上出現的類似定義，體現了“知識之諧”;教師點評了圓的兩種定義，也讓學生點評了數學史上圓柱的各種定義，找到了最簡潔、完善的定義，體現了“方法之美”;學生用不同的學具，以小組合作的方式，逐步探究出圓柱的定義，參與到知識生成的過程中，體現了“探究之樂”;學生從生活問題中抽象出幾何體，用類比的推理方式得到圓錐、球的概念，歸納出一般旋轉體的概念，提升了數學抽象、直觀想象和邏輯推理等能力，體現了“能力之助”;教師展現了東、西方的圓柱形建筑、物體以及不同時空的數學家對圓柱定義的不斷完善過程，揭示了數學背后的多元文化和人文精神，體現了“文化之魅”;通過旅游景點的推薦提升了學生的數學學習興趣，在圓柱概念的不斷完善過程中培養了學生動態發展的數學觀，同時，通過數學家對真善美的追求，讓學生受到了鼓舞，也學會了尊重和包容，體現了“德育之效”。

當然，在本節課中，教師并未引導學生將圓柱與棱柱概念進行對照，是一個遺憾。在未來的教學中，教師可以在學生的課后作業中設置這一部分內容，讓學生對幾何體的概念和形成有更系統的理解。

本文系本刊連載的汪曉勤教授團隊開發的HPM案例之一，也系華東師范大學HPM工作室開發的系列課例之一。

參考文獻：

[1] 張頡.多面體和旋轉體的教學[J].數學教學，1983（6）.

[2] 王志明.談立體幾何第三章“旋轉體”的教學[J].數學教學，1959（8）.

[3] 張頡.談談立體幾何《多面體與旋轉體》的教學體會[J].數學通報，1984（11）.

[4] 喬敏.《多面體和旋轉體》的數學思想方法與教學實踐[J].數學通報，2001（7）.

[5] Wang，X.，Qi，C.，Wang，K.A Categorization model for educational values of the history of mathematics[J].Science & Education， 2017（7-9）.

[6] ﹝古希臘﹞歐幾里得.幾何原本[M].蘭紀正，朱恩寬，譯.西安：陜西科學技術出版社，2003.

[7] Heath，T.L.The Thirteen Books of Euclids Elements[M].Cambridge：The University Press，1968.

[8] 郭書春.九章算術譯注[M].上海：上海古籍出版社，2009.

[9] Hayward，J.Elements of Geometry[M].Cambridge：Hilliard and Brown，1829.

[10] Newcomb，S.Elements of Geometry[M].New York：H.Holt，1884.

[11] Bartol，W.C.Theelements of SolidGeometry[M].Boston：Leach，Shewell & Sanborn，1893.

[12] Beman，W.，Smith，D.E.New Plane and Solid Geometry[M].Boston：Ginn & Company，1900.