創設數學思維情境，引導學生發現數學規律

韋豪將 郭利群

數學研究對象是形式化的思想材料，憑借數學語言和數學符號為思維載體，并以認識和發現數學規律為目的，進行表述、推理、歸納、交流和解決問題的一種思維活動。

一、創設操作情境，引發學生動作思維，發現數學規律

動作思維也稱直觀動作思維，在思維過程中依賴實際動作來進行思考、發現與解決問題的思維活動。其基本特點是動作與思維不可分開，離開了動作就不能思維，依靠實際操作與當前的感知覺來進行思考發現新知。

如教學“三角形”這部分知識時，首先讓學生拿出課前準備用的長方形紙片按對角線剪下，分成兩個三角形，教師點撥剪下這兩個三角形來重疊一下，你們發現了什么？經過學生動手操作后，由動作思維引向形象思維，有的說兩個三角形大小一樣，面積相等。有的說每個三角形都有一個角是直角。有的又補充說：另外兩個角的和是90°，因為他們是由長方形的一個角分出來的。此時水到渠成，教師因勢利導，讓學生自己歸納出：

1.三角形內角的和=長方形內角和的一半=90°×4÷2=180°

2.直角三角形的面積=是長方形面積的一半=長×寬÷2

用同樣的方法 ，再給學生把平行四邊形的紙片按對角線剪下，讓學生在前例的基礎上進行發散思維，學生紛紛動手用量角器分別量兩個三角形的內角和都等于180°，用同樣的方法，學生也歸納出鈍角或銳角三角形的面積=平行四邊行面積÷2=底×高÷2，最后組織學生對上面兩種情況進行推理歸納：

1、任意三角形內角和等于180°2、三角形面積=底×高÷2

學生通過類比，推理、歸納、產生飛躍、發現數學規律，激發學生的思維火花和求知欲望。

二、借用實物實圖，引發學生形象思維，發現數學規律

實物演示或計算，幫助學生形象思維。例如在學生掌握圓柱體體積計算的基礎上學習圓錐體體積計算時，首先讓學生形象觀察圓柱體和圓錐體，它們有哪些異同？它們之間體積存在什么關系？學生通過兩者的比較，都說底面積一樣，高度一樣，但體積不一樣，但不知道圓錐體體積是怎樣求出？教師就學生的質疑進行演示，用開口的圓錐杯盛滿水倒入開口等底等高的圓柱杯子，第一次倒入水位到圓柱杯刻度的 ，第二次倒入水位又上升到刻度的 ，第三次倒入水剛剛盛滿到杯口，如圖。

學生在自己操作實驗后，粗淺認識到等底等高的圓錐體體積等于圓柱體體積的 ，在此基礎上，歸納出兩者之間體積關系一：

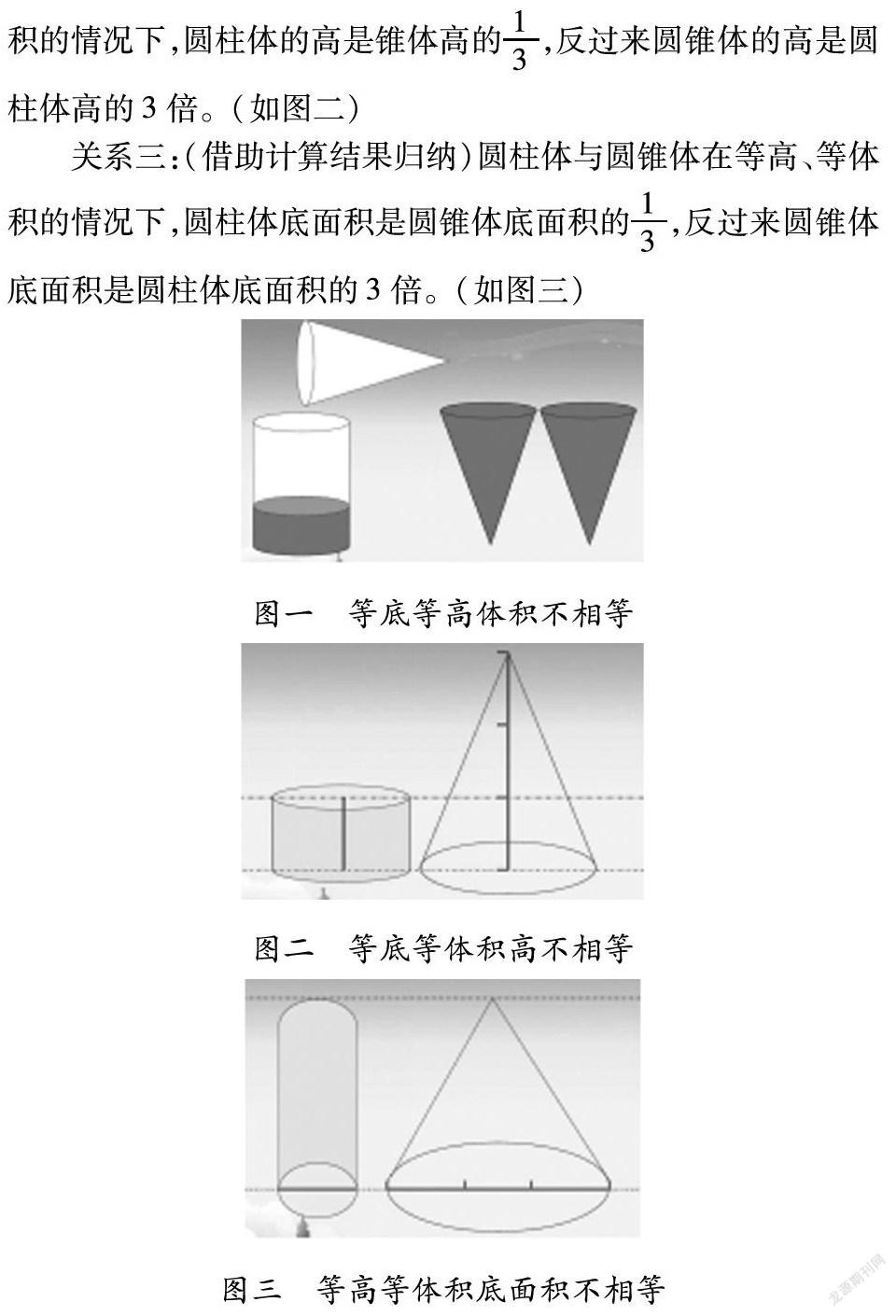
關系一：圓柱體和圓錐體在等底等高的情況下，圓錐體體積是圓柱體體積的 ，反過來，圓柱體體積是圓錐體體積的3倍。

關系二：（借助計算結果歸納）圓柱體與圓錐體在等底等體積的情況下，圓柱體的高是錐體高的 ，反過來圓錐體的高是圓柱體高的3倍。

關系三：（借助計算結果歸納）圓柱體與圓錐體在等高、等體積的情況下，圓柱體底面積是圓錐體底面積的 ，反過來圓錐體底面積是圓柱體底面積的3倍。

在學生通過實際操作，歸納出圓柱體和圓錐體底、高、體積三要素，其中已知兩要素相等時就可以求出另一個要素，就可以解決實際問題。

幫助學生構建正確的表象，使數量關系從抽象到形象的認識，把復雜轉變簡明清晰。

三、創設良好的抽象思維環境，幫助學生感悟

（1）從數量變化關系引導學生推導運算規律。實施讓學生主動發現運算規律的教學，教師要尊重學生，創設寬松和諧的課堂氛圍，做到學生能發現，教師不暗示，樂意讓學生發表見解，鼓勵學生“異想天開”，“創造奇述”。教師要抓住時機，啟發點撥，引導學生推導發現規律。如教學“商不變”性質時，設計練習：①10÷2=5 ②100÷20=5 ③1000÷200=5 ④10000÷2000=5

引導學生從左到右，又從右到左觀察被除數和除數發生什么變化？商為什么不變呢？學生從表象的觀察到推理判斷，很自然地歸納出：“被除數和除數同時擴大或縮小同樣的倍數，商不變”的規律。又如在教學加法交換律時，先讓學生觀察算式：38+12=12+38，560+310=310+560，要求學生口算每題兩邊的和是否相等，兩邊加數位置有什么變化？學生經觀察思考很自然地歸納出：“交換兩個加數的位置和不變”的規律。教師接著指導學生用字母“a+b=b+a”來表示“加法和不變”的規律。

（2）運用知識邏輯移原理，把抽象復雜轉化成形象思維。通過某種轉化過程，把問題歸結到一類典型問題，進行知識遷移，探求事物之間存在的普遍聯系的一種常用的辯證思維方法。如例：某制藥廠生產一批疾病預苗藥，原計劃25人14天完成，由于急需，要求提前4天完成，需要增加多少人？解此題時工作總量很抽象，教師提示學生思考這是一道比較抽象的工程問題，工作總量不變，但又沒有具體的數字，要求多少天完成也沒有直接給出，我們如何進行解答？學生經短時的交流后，紛紛搶答：25人14天完成已告訴我們工作總量，提前4天是已知的工作時間，計算時只多了一個步驟而已。

抽象思維的轉化擴展，是深化認知的首要步驟，是化歸法的邏輯原理，在教學中要逐步滲透，按照反復引導——初步認識——發現規律的路徑進行。作為教育者，調動學生思維的積極性和主動性，激發學生去發現、去探索、去創造，是時代賦予教師的神圣使命。