一類具比例時滯遞歸神經網絡的全局穩定性及仿真

邢 琳，周立群

（天津師范大學數學科學學院，天津300387）

遞歸神經網絡（RNNs），包括Hopfield 神經網絡、Cohen-Grossberg 神經網絡和細胞神經網絡等，其在信號處理、聯想記憶、優化與控制和人工智能等方面有著重要的應用.這些應用大多要求平衡點的穩定性，由于系統在運行過程中時滯普遍存在，因此研究具時滯的遞歸神經網絡的穩定性更有實際意義.

比例時滯作為一種無界時變時滯，在物理、生物、電子與計算科學等領域發揮著重要的應用.目前對比例時滯遞歸神經網絡的穩定性的研究已取得了一些成果[1-16].文獻[1-4]分別利用M-矩陣理論、時滯微分不等式、Young 不等式以及Lyapunov 穩定性理論，得到了比例時滯遞歸神經網絡全局指數穩定的充分條件.文獻[5]應用定點理論和不等式分析技巧，研究了比例時滯競爭神經網絡的指數穩定性.文獻[6-7]應用Lyapunov 穩定性理論與相關不等式技巧，分別研究比例時滯脈沖二階Hopfield 神經網絡的全局指數穩定性以及比例時滯遞歸神經網絡的指數同步性.文獻[8]利用微分不等式技巧得到了一類多比例時滯遞歸神經網絡正平衡點的唯一性和廣義指數穩定性.文獻[9-10]應用矩陣理論和Lyapunov 函數，證明了兩類多比例時滯細胞神經網絡的指數穩定性和漸近穩定性.文獻[11]利用非線性測度研究了多比例延時細胞神經網絡的指數穩定性.文獻[12]利用內積性質和矩陣理論，得到了一類比例時滯細胞神經網絡的耗散性.文獻[13-16]分別采用微分不等式技巧和微分包含理論研究了比例時滯非自治細胞神經網絡的全局指數收斂性和有限時間穩定性、比例時滯模糊細胞神經網絡的有限時間同步性以及記憶神經網絡的反同步控制性.本文對于一類比例時滯遞歸神經網絡，運用對角（半）穩定矩陣，并建立合適的Lyapunov 泛函，以及構造時滯微分不等式,得到保證系統全局漸近穩定和全局指數穩定的充分條件,該條件與時滯無關,且與以往結果相比保守性較低.

1 模型與預備知識

考慮如下模型

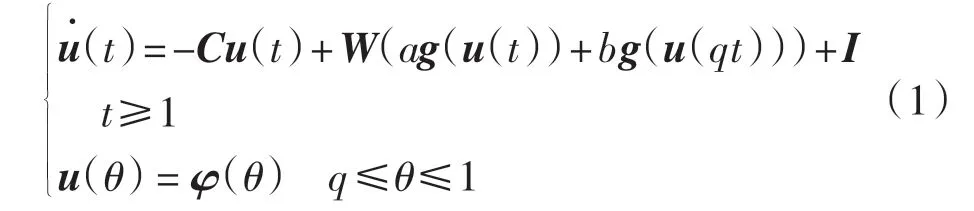
其中：C=diag（c1，c2，…，cn），ci＞0；W=（wij）n×n為神經網絡的權重矩陣；u（t）=（u1（t），u2（t），…，un（t））T為神經元在時刻t 的狀態向量；g（·）為激活函數，g（u（t））=（g1（u1（t）），g2（u2（t）），…，gn（un（t）））T；I=（I1，I2，…，In）T為偏置性輸入；a、b∈R，a ＞0，b ＞0；qt=t-（1-q）t，滿足0 ＜q≤1，（1-q）t 為時滯函數，且當t→+∞時，（1 - q）t→+∞（q≠1）； φ（θ）=（φ1（θ），φ2（θ），…，φn（θ））T∈C（[q，1]，Rn）為系統的初始函數，C（[q，1]，Rn）表示從[q，1]到Rn的所有連續函數構成的集合.

做變換

由系統（1）知et≥1，因此t≥0，且有由系統（1）和式（2）可得

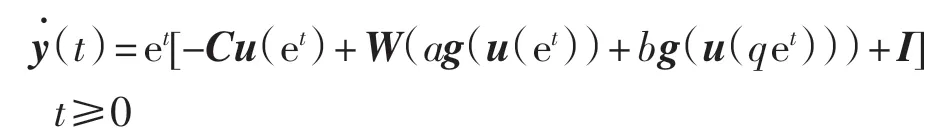
于是系統（1）可等價變換為

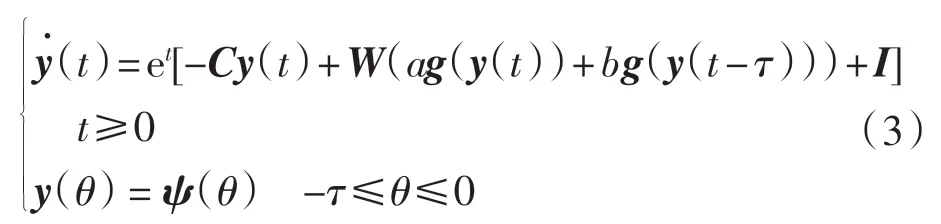
其中： τ=-ln q≥0； y（t）=（y（1t），y（2t），…，y（nt））T，ψ（θ）=（ψ（1θ），ψ（2θ），…，ψ（nθ））T∈C（[-τ，0]，Rn）.

假設g（·）滿足如下條件：（H）激活函數gi滿足連續的局部Lipschitz 條件，且為一致不減的函數，即對于任意常數xi0∈R，?εi0＞0，li0＞0，i=1，2，…，n，使得

其中：σ、ρ∈[xi0-εi0，xi0+εi0]，σ≠ρ.

設系統（1）的平衡點為u*, 系統（3）的平衡點為y*，由假設（H）知系統（1）和系統（3）的平衡點均存在,且易證u*=y*.令z（t）=y（t）-y*，則系統（3）可變換為

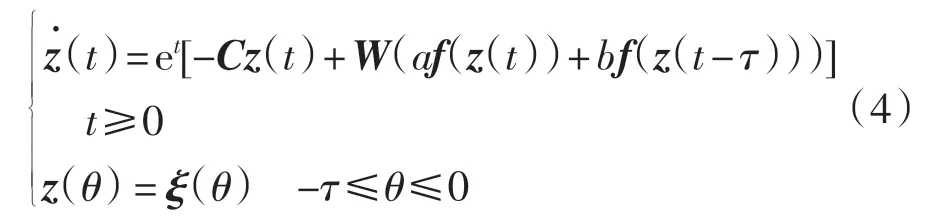
其中：f（z（t））=（f1（z1（t）），f2（z2（t）），…，fn（zn（t）））T=g（z（t）+y*）- g（y*），f（0）=0； ξ（θ）=ψ（θ） - y*.f 也滿足條件（H），因此,系統（4）零解的穩定性與相應的系統（3）的平衡點的穩定性等價.

定義1稱n×n 矩陣A 為對角半穩定的（或對角穩定的）,如果存在正對角矩陣K，使得KA+ATK≤0（或KA+ATK ＜0）.

定義2稱系統（4）的平衡點z*=0 是全局漸近穩定的,如果對于任何初始值都有

定義3稱系統（4）的平衡點z*=0 是全局指數穩定的,如果存在M≥1，β ＞0，使得

定義4設存在ai＞0，使得|zi（t）|≤ai，?t≥0，i=1，2，…，n.記

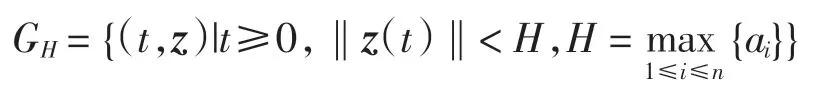
若在GH內存在正定函數V（z（t），t），使得則系統（4）的零解是穩定的.

命題1[17]存在正函數li（zit），i=1，2，…，n，滿足

命題2[17]存在正連續變量li0滿足

?sit=即sit是介于0 與zit之間的函數，D+fi（sit）為fi（sit）的Dini 導數.

命題3[17]存在正連續變量li0，i=1，2，…，n，滿足

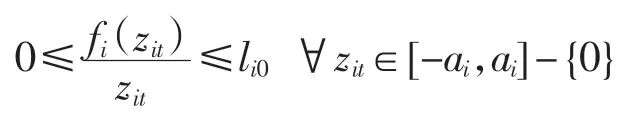
2 主要結果

定理1若系統（1）中矩陣W 是對角穩定的,且滿足條件（H），則系統（1）的平衡點是全局漸近穩定的.

證明因為W 是對角穩定的,因此存在正對角矩陣K=diag（k1，k2，…，kn），使得KW+WTK ＜0.考慮如下Lyapunov 泛函

由命題1 知V（t）≥0，即V（t）是正定的.易知afi（zi（t））+bfi（zi（t-τ））滿足條件（H）.對V（t）沿系統（4）對t≥0求導，得

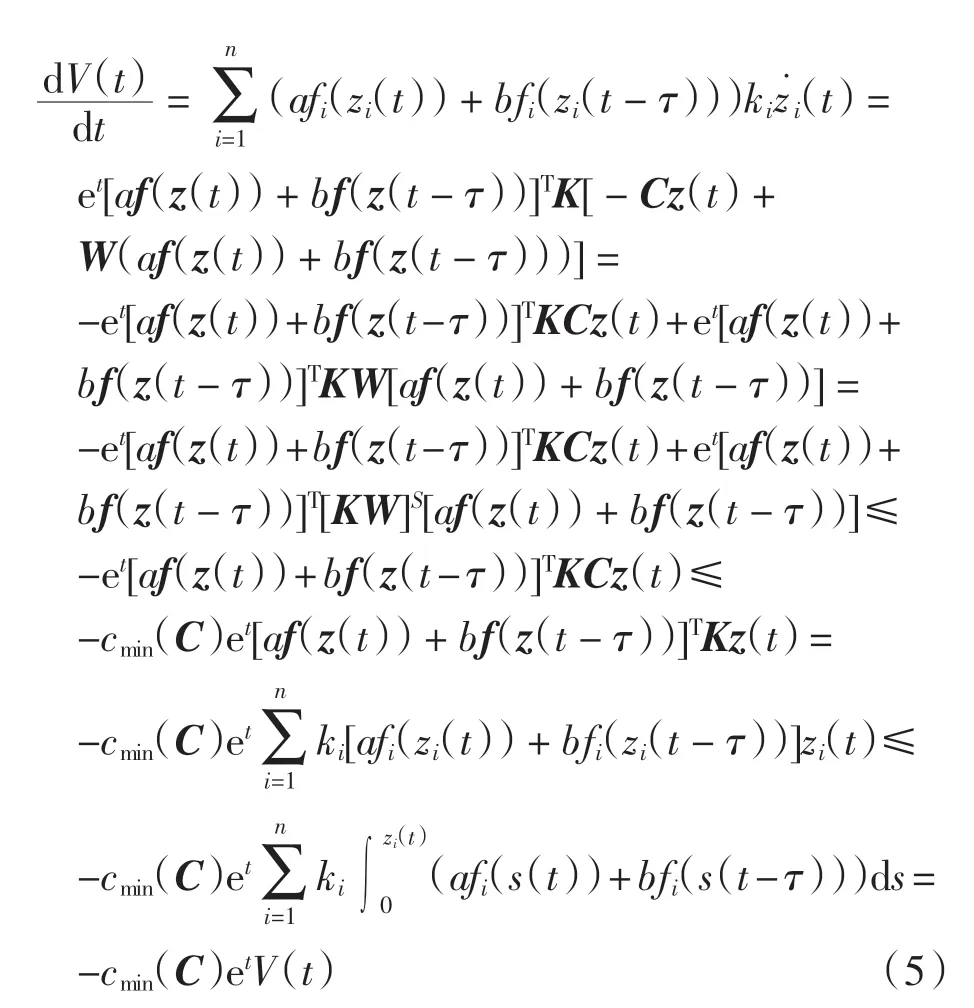
其中cmin（C）表示矩陣C 的最小的特征值.

設z（t）≠0，則存在某個i,使得zi（t）≠0，由V（t）的定義知V（t）＞0，再由式（5）得

考慮z（t）=0，若z（t -τ）=0，由式（5）得

利用一塔兩線模型分析得到的系統振動特性,與三塔兩線等其他更為復雜的模型得到的結論基本一致[13].因此,可以將多跨連續的塔-線體系結構簡化為一基塔與兩跨線組成的簡化系統,如圖1所示.將塔-線體系中的輸電塔、導線分別視為懸臂梁和弦線,得到的一塔兩線連續體簡化力學模型[14].

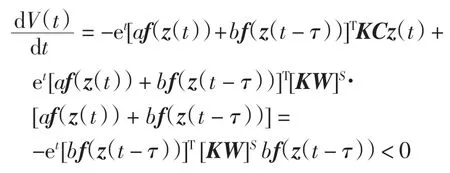
設z（t）=0，z（t-τ）=0，此時顯然有

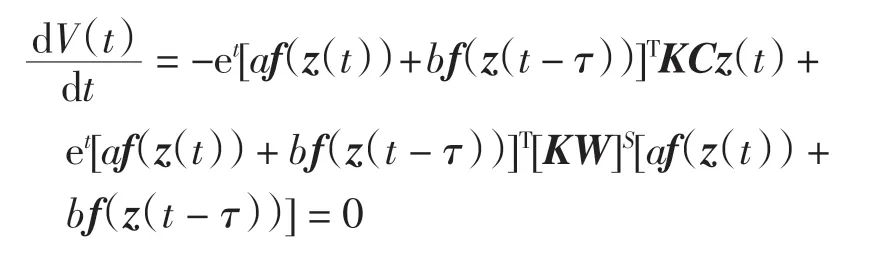
定理2若系統（1）中矩陣W 是對角穩定的,且滿足條件（H），并且存在常數α ＞0，使得

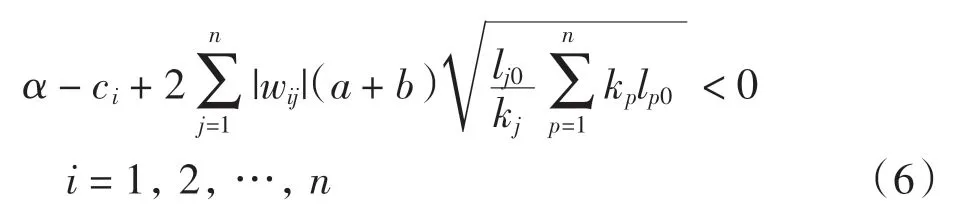
則系統（1）是全局指數穩定的.

證明仍考慮定理1 中的Lyapunov 泛函,由定理1 知系統（4）的零解z（t）=0 是全局漸近穩定的.由定義2 知，存在ai＞0，使得|zi（t）|≤ai，?t≥0，i=1，2，…，n.

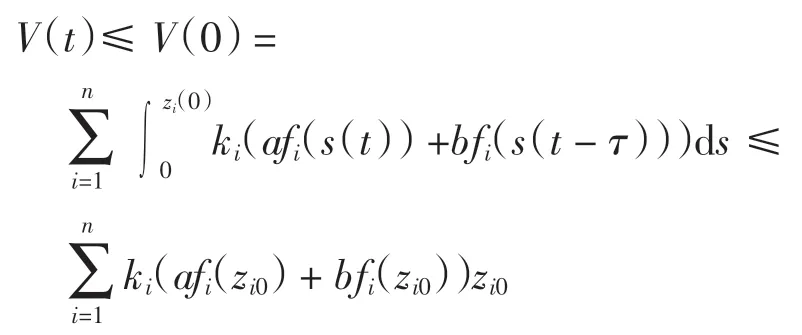
由命題3 得

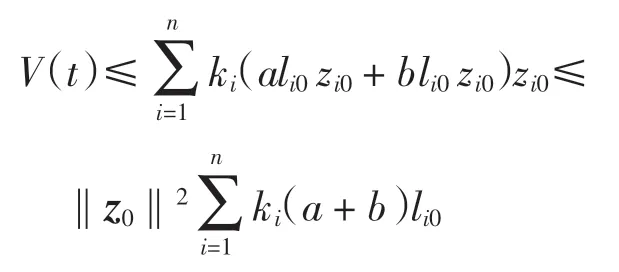
其中z0=（z10，z20，…，zn0）T.定義如下連續函數

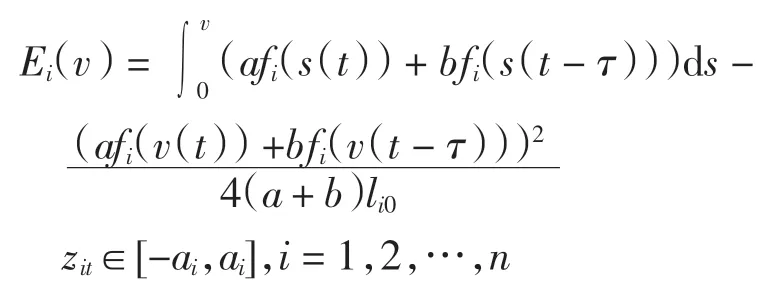
對Ei（v）取Dini 導數,得

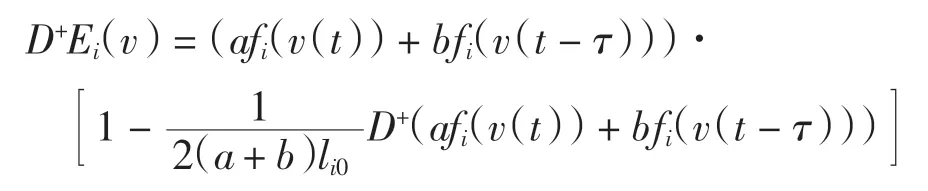
由命題2 可知

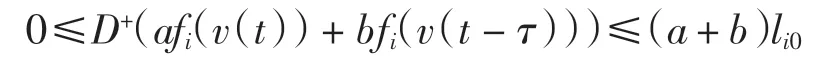
于是有

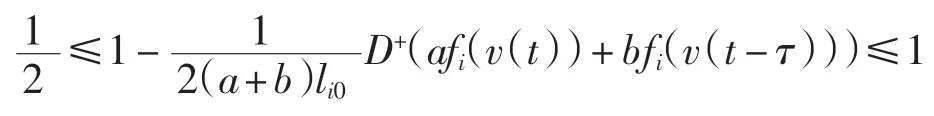
從而

由命題3 得

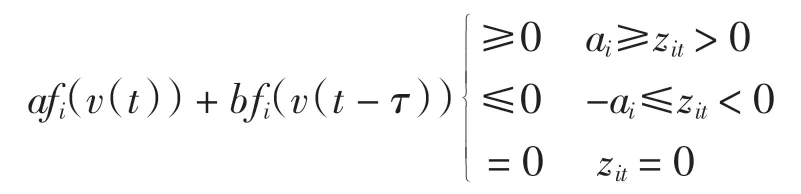
所以

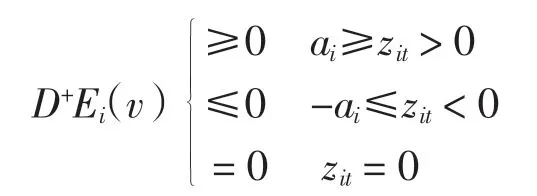
于是?zit∈[-ai，ai]，Ei（v）≥Ei（0）=0，即有

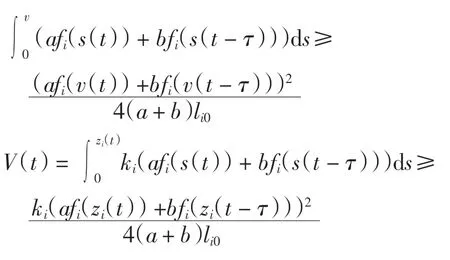
于是有

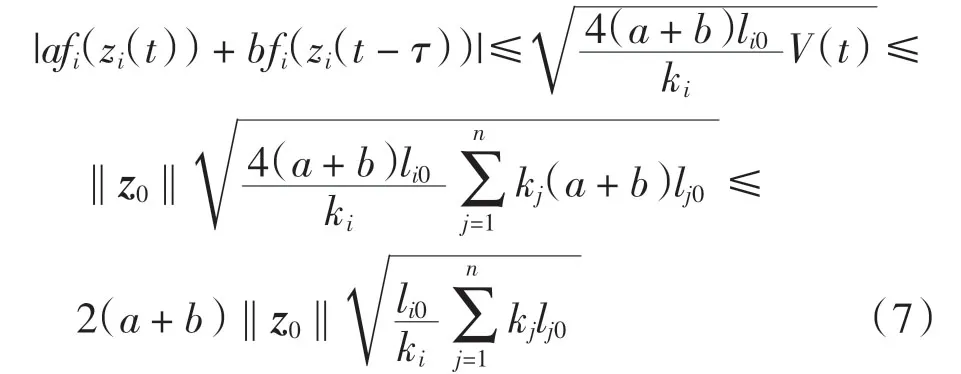
定義

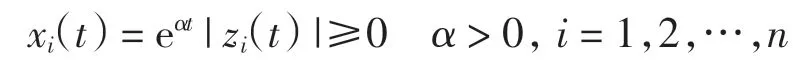
由式（4）及式（7）可得

因此

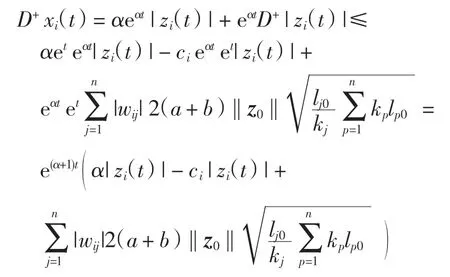
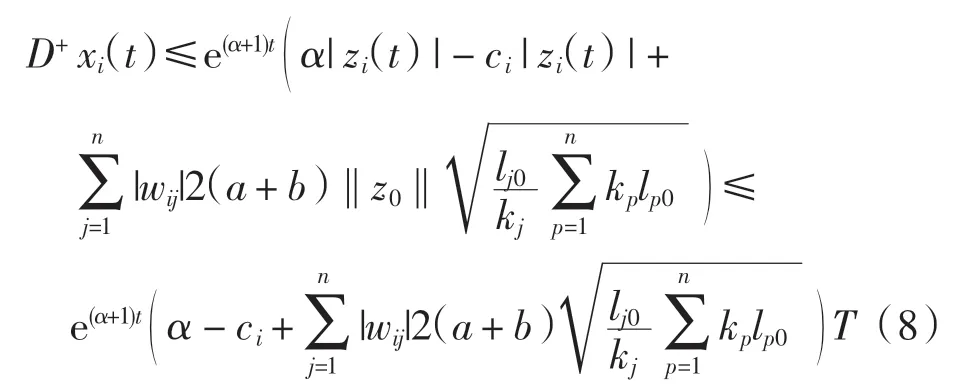
由此不難得到

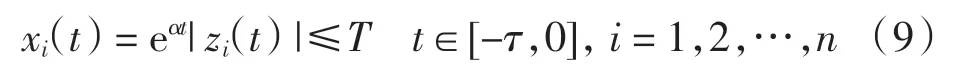
斷言xi（t）≤T，i=1，2，…，n，t∈（0，+∞）.先證對d ＞1，有

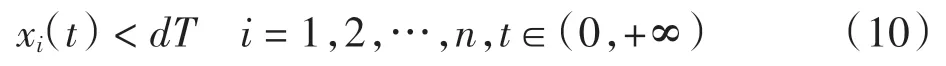
若式（10）不成立，則由式（9）可知存在t1＞0 和某個i（不妨設為k），使得

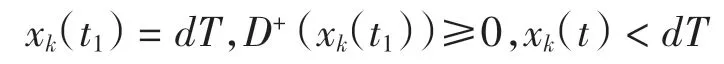
其中：-τ≤t ＜t1，i=1，2，…，n.

另一方面，由式（6）和式（8）有

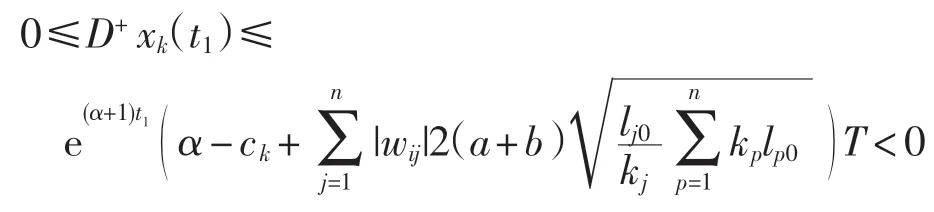
因此得到矛盾.于是有

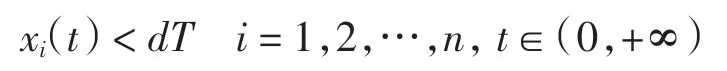
當d→1 時，有

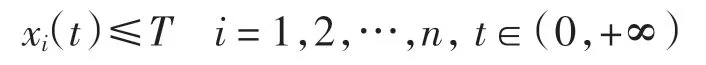
于是可得

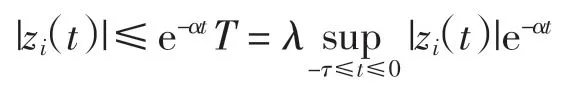
其中α ＞0，λ≥1，i=1，2，…，n.由定義3，系統（4）的零點是全局指數穩定的，從而系統（1）的平衡點也是全局指數穩定的.

定理3若系統（1）中矩陣W 是對角半穩定的，且滿足條件（H），則系統（1）的平衡點是穩定的.

證明對于定理1 中的Lyapunov 泛函，當z（t）=0，z（t-τ）≠0 時，由式（5）有

其余過程同定理1.由定義4 知系統（4）的零解是穩定的，則系統（1）的平衡點是穩定的.

3 數值算例及仿真

例考慮如下二維模型

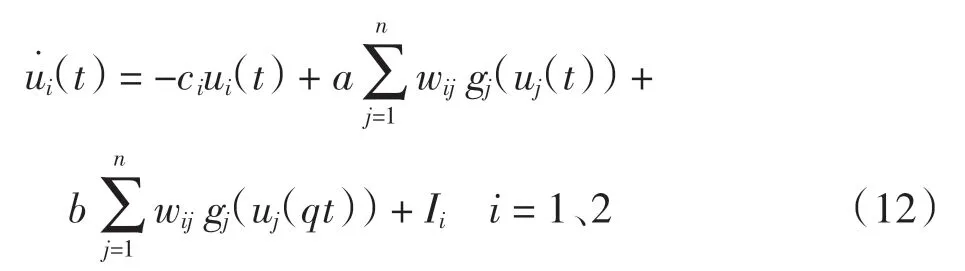
其中

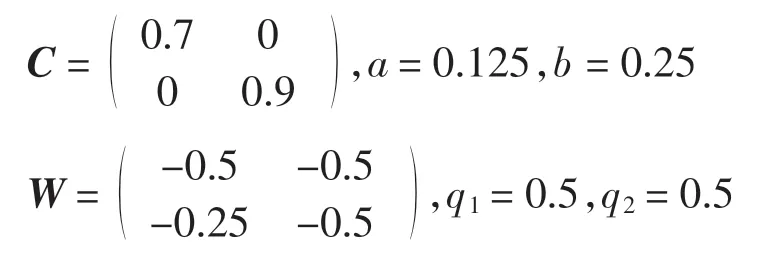
故有

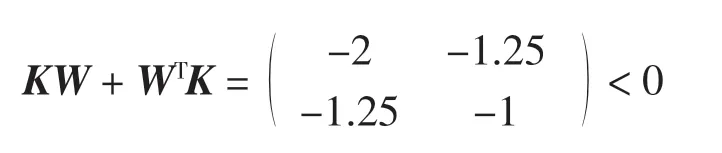
取α=0.001，計算得

故滿足定理2 的條件，則系統（12）的平衡點是全局指數穩定的.

當系統（12）外部輸入I=（0，0）T時，系統平衡點是（0，0）T.系統（12）的全局指數穩定性見相軌跡圖1和時間響應曲線圖2.

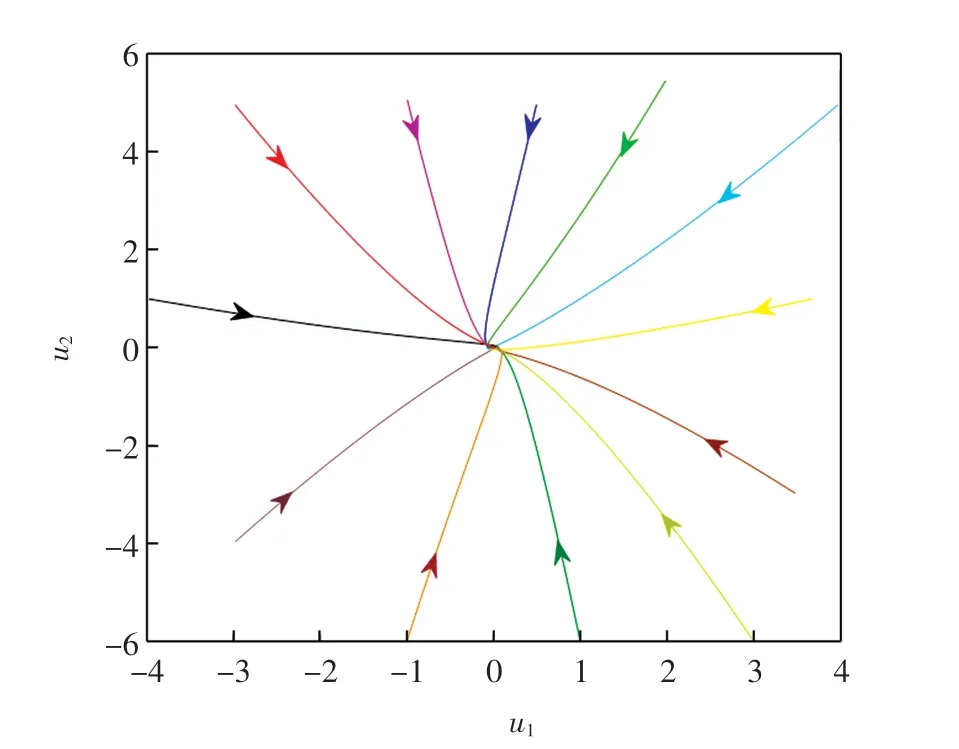
圖1 當I=（0，0）T 時，系統（12）的相軌跡Fig.1 Phase trajectory of System（12）when I=（0，0）T

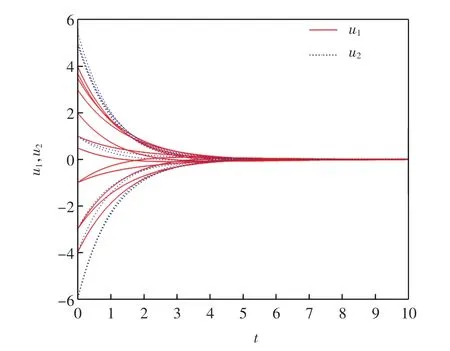
圖2 當I=（0，0）T 時，系統（12）的時間響應曲線Fig.2 Time response trajectory of System（12）when I=（0，0）T

當系統（12）外部輸入I=（1，-1）T時，應用Matlab計算得系統平衡點為（1.329 6，-1.097 5）T.系統（12）平衡點的全局指數穩定性見相軌跡圖3 和時間響應曲線圖4.

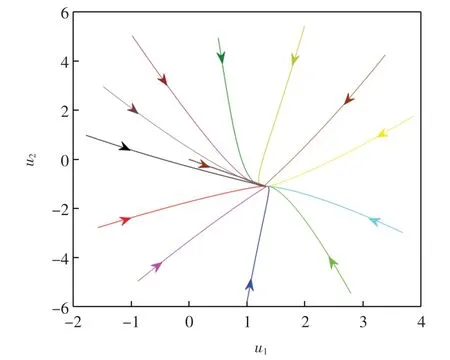
圖3 當I=（1，-1）T 時，系統（12）的相軌跡Fig.3 Phase trajectory of System（12）when I=（1，-1）T

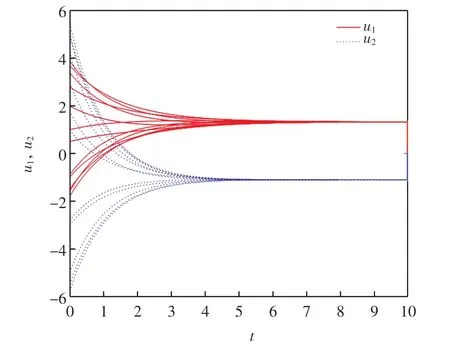
圖4 當I=（1，-1）T 時，系統（12）的時間響應曲線Fig.4 Time response trajectory of System（12）when I=（1，-1）T