滬科版初中數學教學中融入數形結合思想之實踐

余贊東

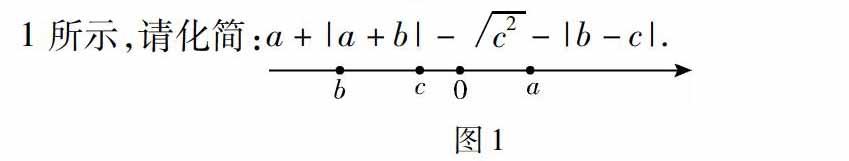
【摘要】數形結合思想是數學學科的一個重要內容，在滬科版初中數學教材中有許多內容都充分體現了數形結合的思想，讓數學問題從原有的抽象化轉變成為現有的直觀化，能夠讓學生充分理解數據關系，并從本質上理解圖形的幾何屬性，幫助學生降低抽象數學題的解題難度.因此，本文主要針對滬科版初中數學教學與數形結合思想的融合教學策略.

【關鍵詞】初中數學;數形結合;數據關系;幾何

數形結合實際上反映了數與形之間的對應關系，能夠利用數與形的互相轉化對數學問題進行解決.這主要是因為數形結合具有數學問題生動化與直觀化的特點，學生能夠發揮其形象思維能力，有效理解數學問題中蘊含的知識，并利用現有的知識解決數學問題.在初中數學中，數形結合思想的應用可以降低學生的數學學習難度，消除初中生對數學的畏難情緒.因此，初中數學教師應該積極將數形結合思想滲透在教學過程中.

一、在有理數的數學教學中滲透數形結合思想

在滬科版初中數學七年級上冊有理數這部分數學內容中，教師就可以滲透數形結合思想，增強學生對數形結合思想的運用意識，為學生以后在數學解題中運用數形結合思想而打下良好的基礎.而且有理數本身就是初中學生在數學學習過程中必須掌握的入門知識，在這部分數學內容的學習中學會采用數形結合思想來解題，拓展數學思維能力，并且有效提升數學分析能力.在有理數的實際教學中，數形結合思想一般會被運用在數軸方面，讓學生學會利用數軸來解決數學問題.而數軸實際上屬于一個抽象的內容，教師可利用實物演示的方法幫助學生理解這個概念，使其掌握數軸的數與點之間的關系，進而掌握數形結合思想的概念，學會通過數形結合的方法來分析數學問題中所蘊含的數量關系，以幫助其快速解決數學問題.在有理數的數形結合思想指導下可以解決的數學問題有很多，比如，相反數、絕對值或者與倒數相關的數學問題等等.比如，有這樣的數學問題：有三個實數a，b和c都在同一條數軸上，

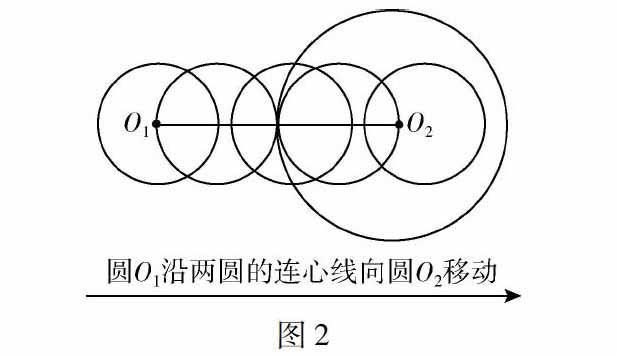
這道題目充分體現了數形結合的思想，根據數軸，學生可直觀地看到三個實數的正負.其中，a這個實數為正數，而b和c這兩個實數則是負數.同時，從數軸中也可以直觀地獲悉三個實數的大小關系.即只有a這個實數大于零，而b和c這兩個實數都小于零，且b

二、在教學中逐層遞進地滲透數形結合思想

在有理數的教學中滲透數形結合思想，實際上是對數形結合思想最簡單地運用.初中數學教師應該將這一重要思想貫穿在滬科版數學教材的始終.因此，教師要引導學生學會正確掌握數形結合思想中的基礎數量關系，并在接下來的數學教學中進行有效的應用，逐層遞進地掌握好數形結合思想的解題技巧.比如，在分解因式的教學中，教師就可以滲透數形結合思想.一般而言，學生在對a2-b2這一因式進行分解時，一般都是分解成為（a+b）（a-b），但是學生卻沒有進一步思考這個分解方式，比如，“為什么通過這樣的分解可以獲得正確的答案？”因此，為了鍛煉學生的思維能力，使其掌握數學本質，教師就可以引入數形結合思想來引導學生展開探究活動.教師可利用多媒體技術來演示：邊長為a的正方形被剪去邊長為b的正方形，可知a>b這個數量關系，而剩余的圖形面積即是a2-b2.通過這樣的數形結合方法，可以讓學生有效理解因式分解的數學原理，降低了學生對這部分知識的理解難度，可以有效增強學生在數學解題中的數形結合應用意識.

三、利用數形結合思想引發學生的深入思考

在滬科版初中數學教材中，存在一些可以引發學生遷移思考的數學內容，教師可充分挖掘這些知識內容，并滲透數形結合思想來啟發學生進行深入的思考.比如，在“兩圓的位置關系”這方面的數學知識中，要求學生從“點、圓的位置關系”以及“直線、圓的位置關系”這些淺層的數學關系中深入思考，對圓和圓之間的位置關系進行了解.這部分的知識存在較強的抽象性，融入數形結合思想，可以有效地將其轉化成為具體和形象的內容，幫助學生理清其中存在的關系，包括外離關系、外切關系、內切關系、內含關系、相交關系等五種位置關系，如圖2所示：

這一圖形非常直觀地展示了兩圓之間所有的位置關系，降低了學生對抽象數學知識的理解難度，同時又可幫助學生在解題時巧用數形結合的方法進行解答.

三、結束語

綜上，數形結合思想在滬科版初中數學中的滲透與應用具有重要的教學價值，能夠讓初中學生樹立起數形結合的解題思想，逐層遞進地了解更深的數學知識，利于提高初中學生的數學問題分析能力與解題能力，同時又可鍛煉其數學思維能力，實現學生對數學的深度學習.

【參考文獻】

[1]王愛花.初中數學數形結合思想教學研究與案例分析[J].中國校外教育，2017（2）：64.

[2]楊雙峰.初中數學教學中數形結合思想的培養策略[J].考試周刊，2016（80）：69.