如何借助導數及其應用培養數學思維
2019-09-17 08:00:46隋玉霞
數學學習與研究 2019年14期
關鍵詞:數學思維
隋玉霞
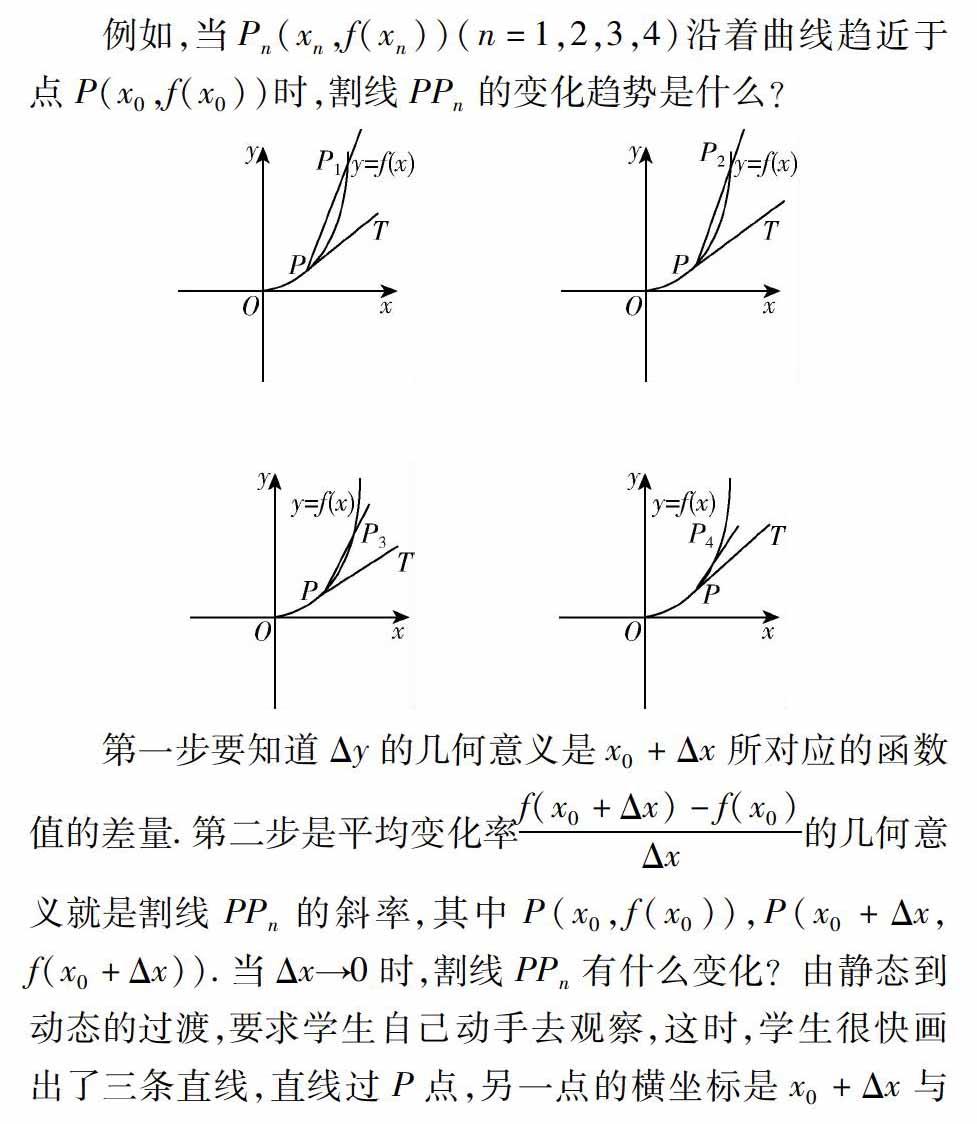

【摘要】導數的幾何意義應用了曲線的切線思想,導數的代數意義應用了變化快慢的數學思想,將數學知識轉化為學生的認知結構,進而培養學生的數學思維,就要設置一些問題情境,讓學生通過觀察與分析構建起自己的認知體系.
【關鍵詞】導數;數學思維;數形結合
數學以最簡約、最概括的方式反映著人類對事物數量關系及空間位置關系的認識,是科學真理的客觀反映.通過數學教育,培養實事求是、言必有據的數學思維形式,為學生接受高等教育打下堅實的基礎.導數是對函數性質的一個研究途徑,也是高等數學中微積分的核心概念.通過導數的學習培養學生數學思維,首先要了解導數中蘊含的數學思想,然后再由教師設計教學模式進行有針對性的培養.
一、導數中的數學思想
教材當中設計了兩條線索作為導數的起源,一個是自然界中廣泛的變化現象;一個是變量變化速率的幾何表示.這也說明,導數中蘊含著數形結合的思想、變化的思想.
二、如何通過教學設計培養學生的數學邏輯思維
(一)重視知識結構到認知結構的轉化
數學知識結構是由數學概念和命題構成的,要將這些新的知識結構轉化為學生的認知結構,只有通過學生的動手觀察、探索,將新的知識結構與舊的知識結構建立聯系,例如,導數數形結合的切線表示法,以及導數的變化快慢的代數表示法,就是用舊知識解釋新知識,從而轉化學生的認知結構的.
(二)從數學史的角度把握知識的形成過程
從數學史的角度來看,導數的發現與伽利略有關系,當時伽利略發現了自由落體運動的規律,可以根據加速度與時間的關系求出落體的瞬時速度,當△t很小時這個比值接近于時刻t的瞬時速度,這就是導數的啟蒙.
【參考文獻】
[1]梁霜.數形結合的思想在導數問題中的應用[J].數學學習與研究:教研版,2018(16):155.
猜你喜歡
都市家教·上半月(2016年11期)2016-11-30 18:55:58
考試周刊(2016年88期)2016-11-24 13:52:54
散文百家·下旬刊(2016年9期)2016-11-23 02:14:52
數學學習與研究(2016年19期)2016-11-22 10:50:58
數學學習與研究(2016年19期)2016-11-22 10:46:14
讀寫算·素質教育論壇(2016年22期)2016-11-14 06:39:19
讀寫算·素質教育論壇(2016年21期)2016-11-14 05:30:52
考試周刊(2016年84期)2016-11-11 22:57:22
情感讀本·理論篇(2016年9期)2016-11-05 17:08:37
考試周刊(2016年79期)2016-10-13 22:13:30

