深埋隧洞三岔口圍巖穩定性計算理論

饒軍應，謝財進，趙霞，劉燈凱，聶崇欣，劉寧

(貴州大學土木工程學院，貴州貴陽，550025)

隨著我國交通行業飛速發展，隧洞建設規模越來越大，隧洞也越修越長，對技術的要求越來越高。為滿足隧洞工期及運營通風需求，需要增設斜井、橫通道等輔助坑道，而輔洞與主洞連接處會形成三岔口。從力學角度分析，隧洞主洞的圍巖受力通常可視為平面進行求解，當存在輔助坑道介入主洞時，三岔口區的圍巖受力將變得十分復雜，該區域內的開挖易造成隧洞圍巖的受力狀態由最初的三向受力轉變為開挖后的單向或二向受力，且應力分布也截然不同，若未探明三岔口區圍巖應力的分布情況，貿然掘進會增加施工風險。三岔口區圍巖極易松動、掉塊或坍塌，是隧洞開挖時的薄弱點，需予以特別關注，為此，有必要研究三岔口處圍巖受力分布[1-3]。近年來，學者們就隧洞三岔口處圍巖穩定性開展大量研究，基于已有文獻可知，主要有數值分析和應用研究2 個大類[4-12]。在數值分析方面，羅彥斌等[13]通過現場實測和有限元數值模擬，研究了橫通道斜交隧洞對主隧洞結構受力及變形的影響，但未涉及理論解析；藺云紅等[14]研究了地鐵暗挖隧洞斜交下穿既有鐵路工程時的地層沉降和塑性區分布，仍依靠數值模擬分析，未涉及理論解析。在應用研究方面，李東海等[15]結合工程實例，對盾構隧洞斜交下穿地鐵車站的施工進行了分析，僅依靠監測數據和工程經驗給出施工指導意見，未給出理論解釋。已有研究成果表明：新建隧洞三岔口區設計、施工的主要依據源于類似工程的數值模擬、施工參數及工程經驗，在理論解析層面還有待加深。本文基于輔助坑道連接隧洞主洞，對其三岔口區圍巖穩定性進行理論探討，以便為類似工程的設計、施工提供理論支撐。

1 隧洞三岔口圍巖應力分析

隧洞開挖后，圍巖應力將重新分布，局部可能出現應力集中，導致變形甚至失穩破壞。圖1所示為隧洞三岔口受力計算分析圖。分析圖1可知：輔洞與隧洞主洞相交成銳角一側(定義為三角區)受力面積小，該區域受應力集中破壞可能性最大。為計算簡便，假設隧洞主洞、輔洞為不同直徑的圓形隧洞，且為深埋隧洞(圍巖應力計算時僅考慮巖體容重與隧道埋深)，此時，隧洞邊界巖體所受應力簡化為垂直應力P(P=γH，γ為巖體容重，H為隧洞埋深)和水平應力q(q=λP，λ是側壓力系數)，忽略圍巖自重的影響。

按彈性理論中的基爾希公式建立如圖2所示的計算模型，計算圍巖中任一點Q(ρ，θ)的應力[16]：

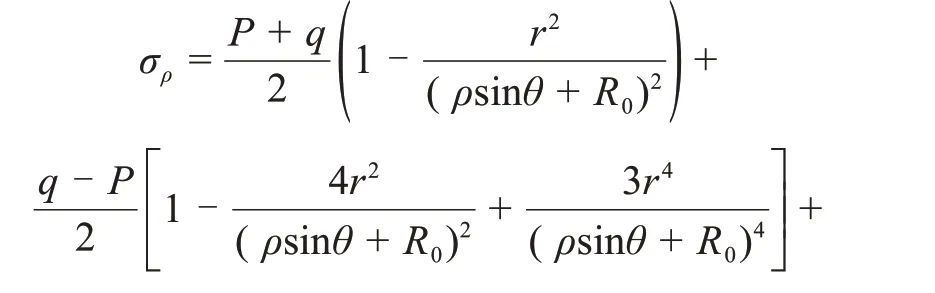
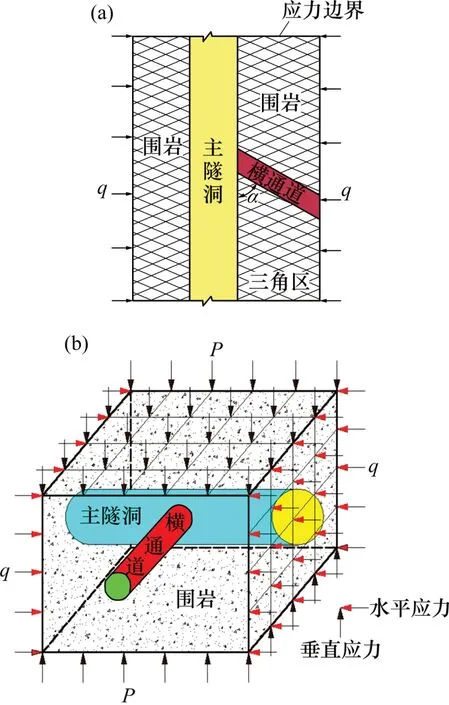
圖1 隧洞三岔口受力計算分析圖Fig.1 Analysis of force calculation of the tunnel three mouths

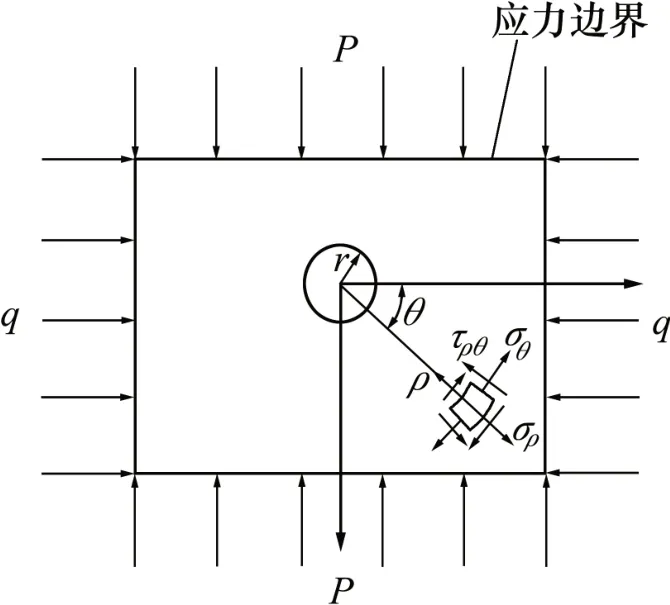
圖2 隧洞圍巖應力分布范圍及計算簡圖Fig.2 Stress distribution range and calculation sketch of tunnel surrounding rock

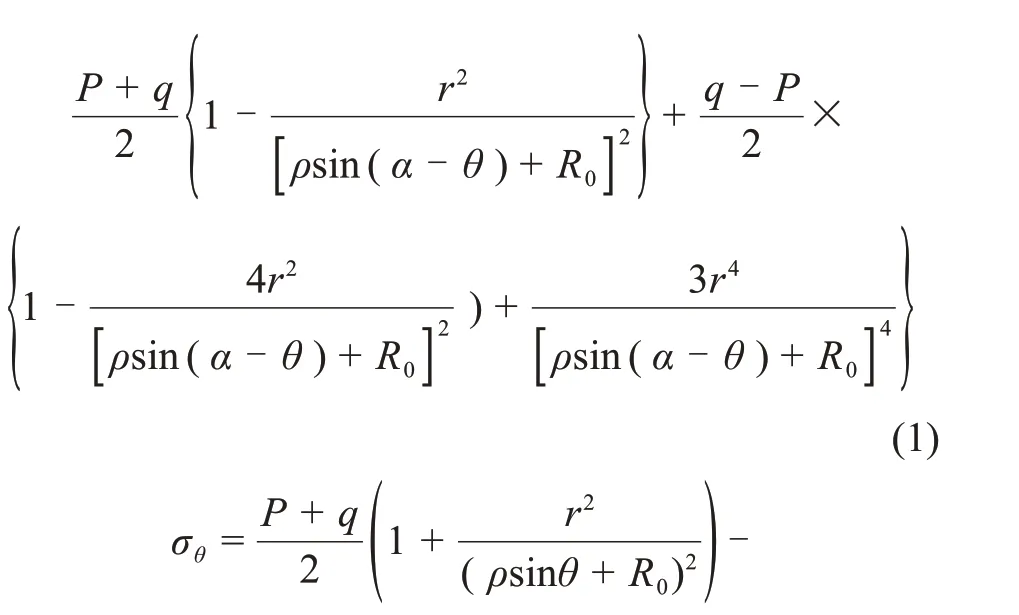
式中：σρ為沿ρ方向的正應力；σθ為沿θ方向的正應力；τρθ為切應力；R0為隧洞三岔口中心至塑性變形圈邊界的距離；r為隧洞主洞開挖半徑；ρ和θ為某點應力的極坐標；α為輔洞與隧洞主洞的交叉角度(銳角)。

根據隧洞三角區域圍巖力學特征及圓形隧洞彈性狀態下圍巖應力計算公式[17]，可得隧洞三角區圍巖垂直應力σh為

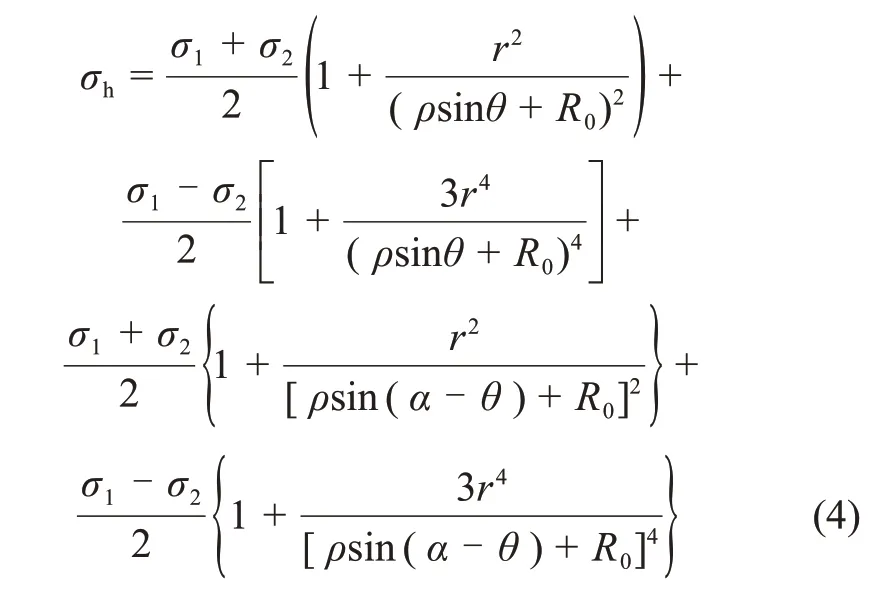
式中：σ1和σ2分別為原巖垂直應力和水平應力，且σ1=P，σ2=q=λP。

將σ1和σ2代入式(4)，可得

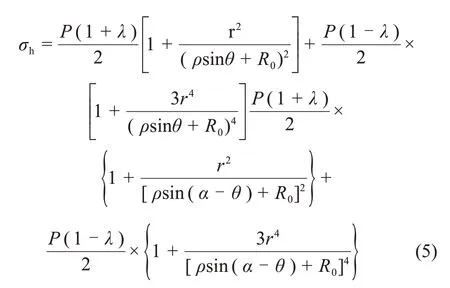
簡化為

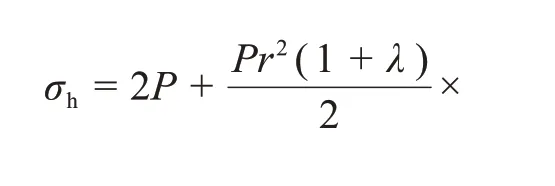
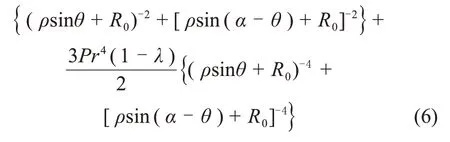
要計算σh，還需求解未知量R0，由卡斯特納(Kastner)公式得：

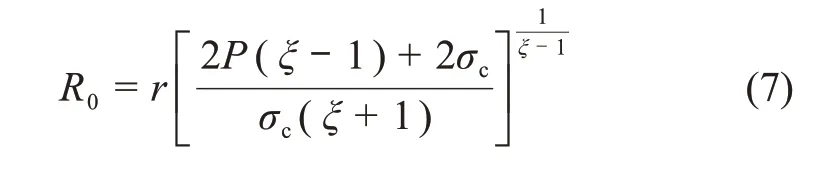
式中：ξ為摩爾圓強度線的斜率；σc為巖石抗壓強度。

由摩爾-庫侖強度理論得：

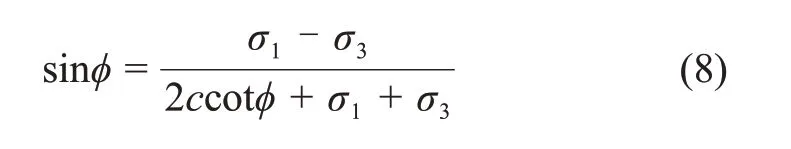
經簡化得

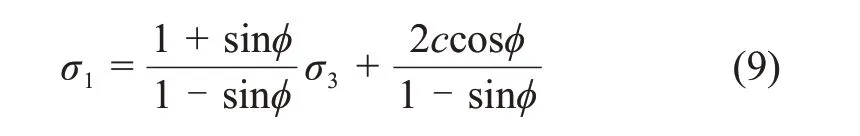
由 于σ1=ξσ3+σc，可 得：(其中：c和?分別為巖體粘聚力和內摩擦角)。

將σc代入式(7)得

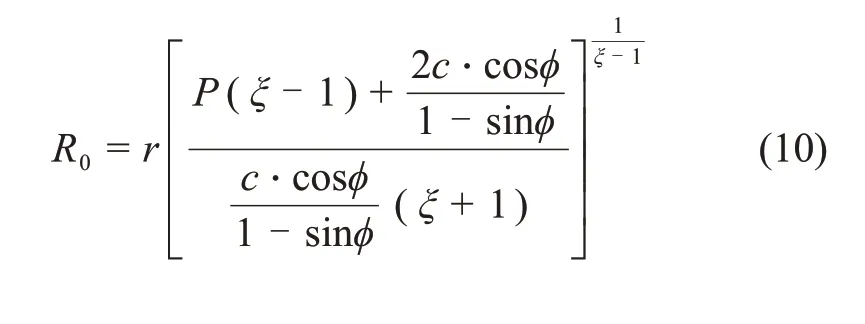
隨著隧洞的開挖，其三角區圍巖應力將重新分布，并伴隨應力集中現象的產生，該區域應力集中的強弱用系數K表示。

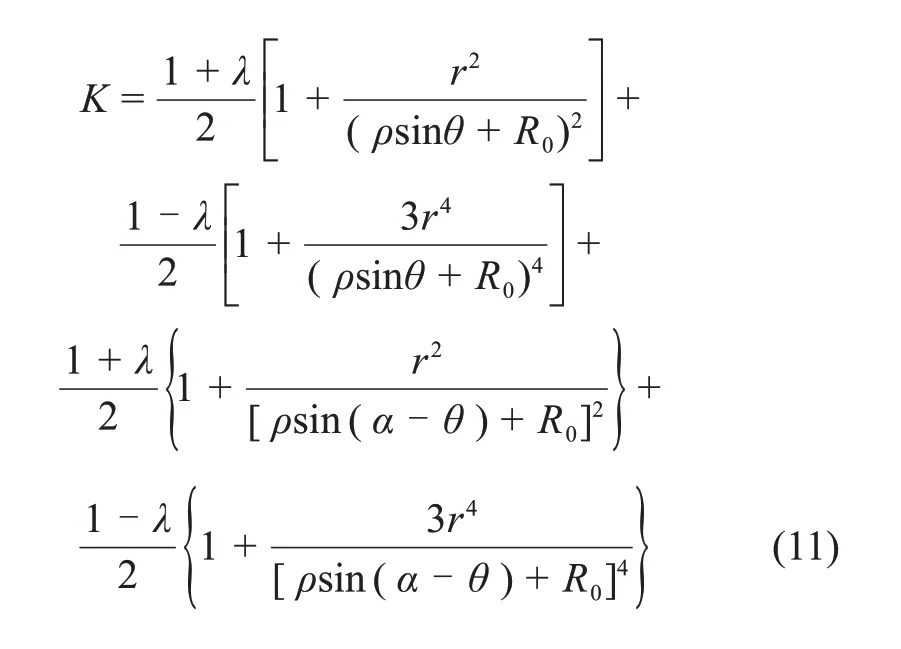
由式(11)可知，三角區圍巖應力與原巖應力、圍巖自身強度、巖體側壓力系數、隧洞截面形狀、尺寸及輔洞與隧洞主洞的交叉角度有關。

2 三岔口圍巖破壞規律分析

2.1 三岔口圍巖破壞深度分析

圖3所示為圍巖狀態分布圖。隧洞三角區圍巖應力集中系數較高，當集中應力大于巖體極限屈服強度時，圍巖由于支撐力不足發生塑性屈服破壞。隨破壞區的擴散，圍巖周圍將依次形成松動區、破碎區、破裂區、塑性區、彈性區和原巖區。圖4所示為彈塑性區圍巖應力分布特征圖。由圖4可見：若集中應力未超過巖體極限屈服強度，可認為圍巖處于極限應力平衡狀態。根據彈塑性區圍巖應力分布，由彈塑性極限平衡理論可知：

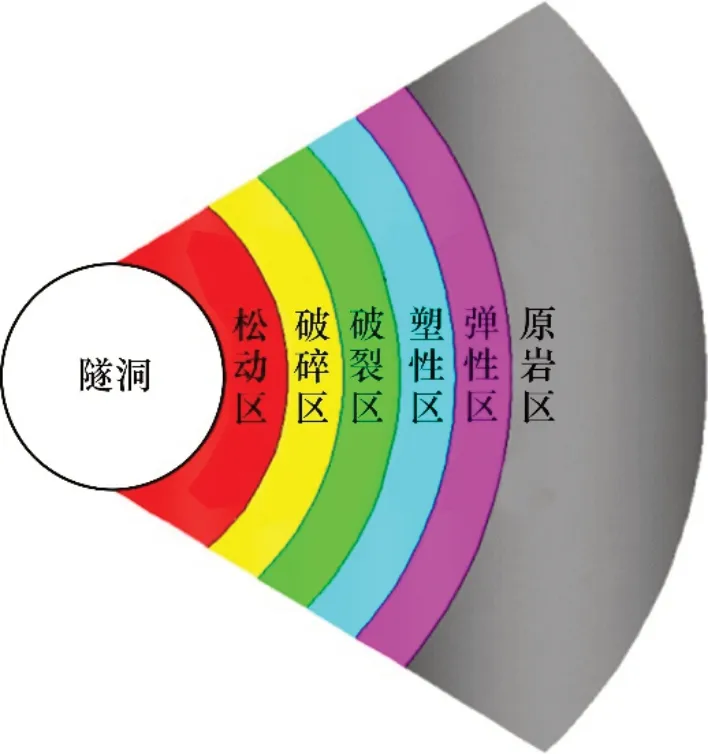
圖3 圍巖狀態分布圖Fig.3 Distribution of surrounding rock state

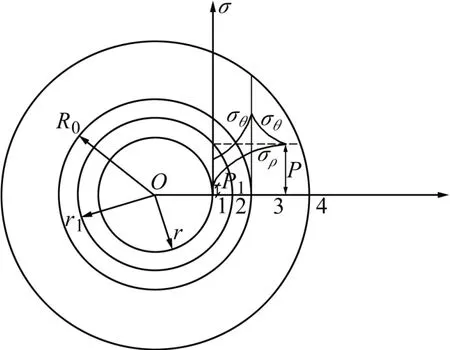
圖4 彈塑性區圍巖應力分布特征圖Fig.4 Stress distribution of surrounding rock in elastoplastic zone

彈性區圍巖應力可描述為[18-19]：

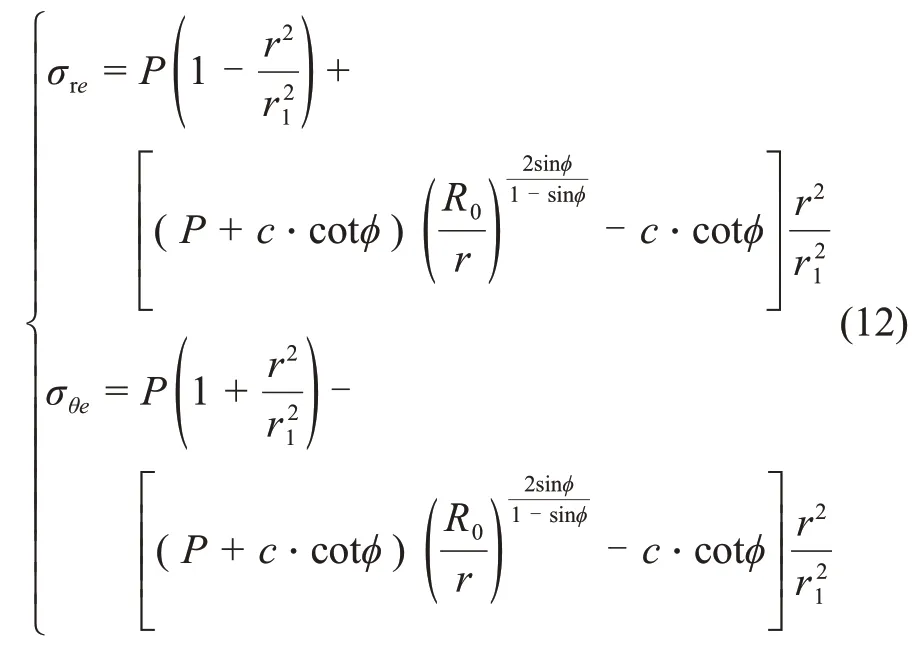
式中：σre為彈性區徑向應力；σθe為彈性區環向應力；r1為松動圈半徑，

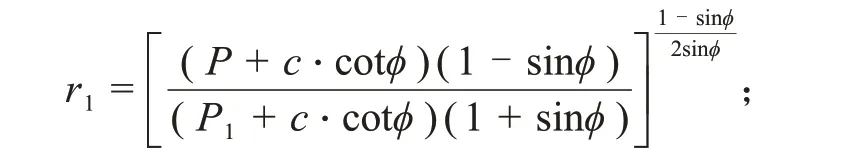
P1為支架反力。

結合式(12)，可知三角區應力疊加后彈性區內沿水平方向的鉛垂應力σx和沿鉛垂方向的水平應力σy為：

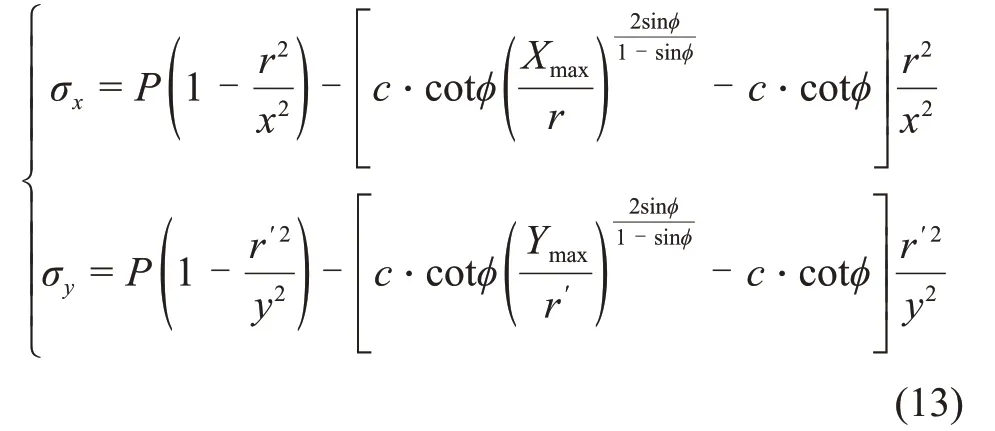
式中：x和y為輔洞與主洞的掘進距離；r′為斜井開挖半徑。

塑性區圍巖應力可描述為[18-19]：

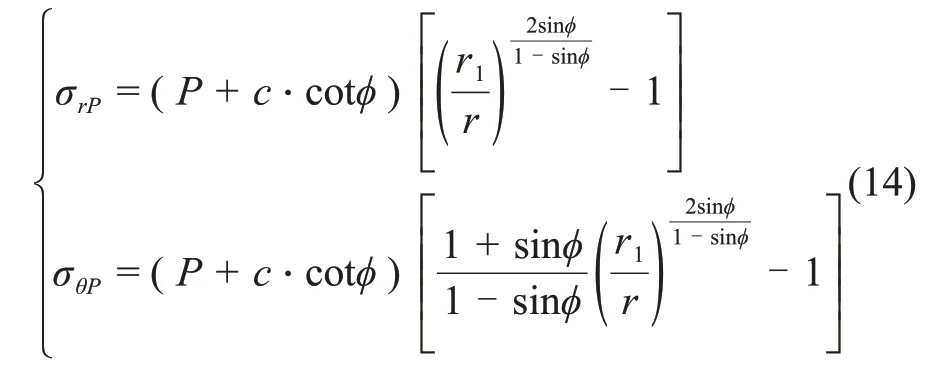
式中：σrP為塑性區徑向應力；σθP為塑性區環向應力。

結合式(14)，可知三角區應力疊加后塑性區內沿水平方向的鉛垂應力σx和沿鉛垂方向的水平應力σy為：

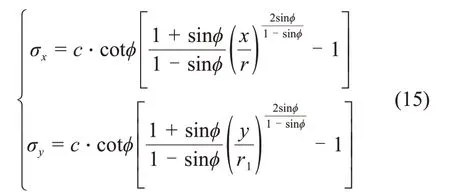
聯立式(13)和(15)解得三角區圍巖水平方向和鉛垂方向的破壞深度為：

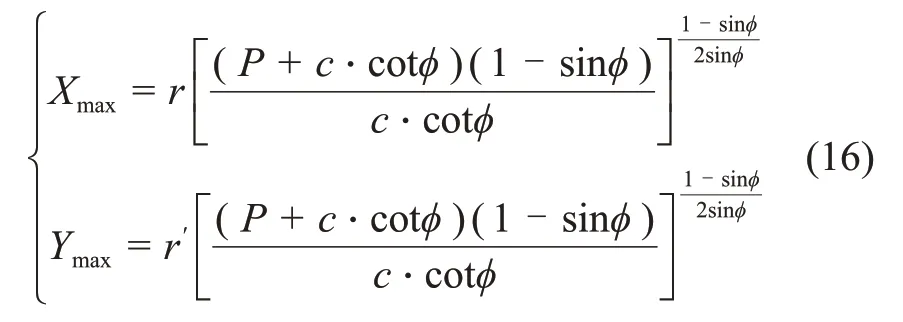
式中：Xmax和Ymax分別為三角區圍巖水平方向和鉛垂方向的破壞深度。

圖5所示為三角區圍巖應力分布及破壞范圍分布圖。由圖5可見：沿x方向的三角區最大破壞深度為Xmax，沿y方向的三角區最大破壞深度為Ymax。

圖5 三角區圍巖應力分布及破壞范圍分布圖Fig.5 Stress distribution and damage range of surrounding rock in triangle area

水平方向鉛垂應力的峰值位于x=Xmax處，為P3；鉛垂方向水平應力的峰值位于y=Ymax處，為P2。2 條應力曲線的交匯處圍巖應力集中系數最大，由數學關系可知圍巖最大破壞深度Q為

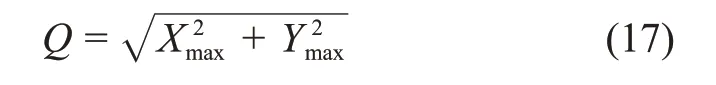
將式(16)代入式(17)得：

由于應力疊加的作用導致三岔口處形成曲邊三角形破壞區，其最大破壞深度與隧洞、輔洞開挖尺寸、原巖應力、巖體自身強度以及輔洞與主洞交角有關。若輔洞進主洞的開挖過度曲線在破壞區域內，則三岔口區圍巖不穩定，需進行加固；反之，三岔口區圍巖穩定。

2.2 三岔口圍巖等效跨度分析

圖6所示為圍巖壓力變化特征曲線。由圖6可見：根據圍巖變形特征分為彈塑性階段(AB段)、小松動變形階段(BC段)、大松動變形階段(CD段)。隧洞三岔口圍巖由于二次開挖導致應力集中，當集中應力大于圍巖極限強度時，圍巖將發生塑性屈服破壞，失去支承能力。在無支護條件下，隧洞頂板將會進入小變形階段甚至大變形失穩破壞階段，主要表現在較軟弱巖層中頂板冒落及隧洞兩幫支撐力不足時頂板彎曲下沉[20-24]。

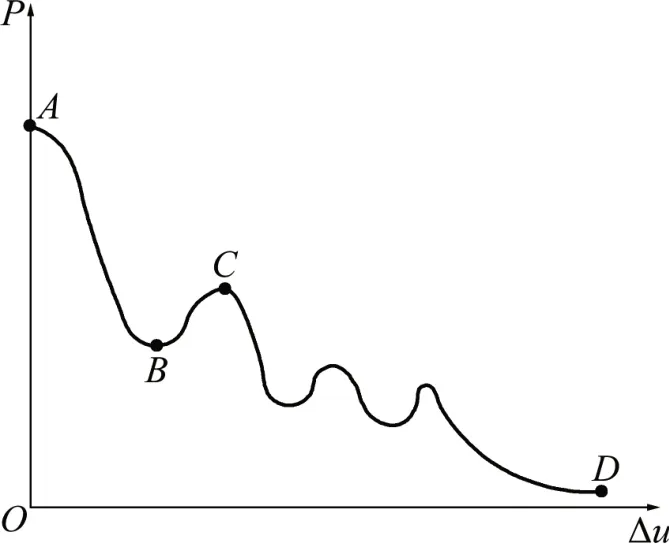
圖6 圍巖壓力變化特征曲線Fig.6 Curve of variation of surrounding rock pressure

圖7所示為隧洞三岔口區跨度示意圖。由圖7可見：頂板彎曲下沉時，基于隧洞三岔口圍巖破壞形式及特征，采用等效跨度理論計算該區域理論最大等效跨度Ltmax和極限等效跨度Lpmax[25]。

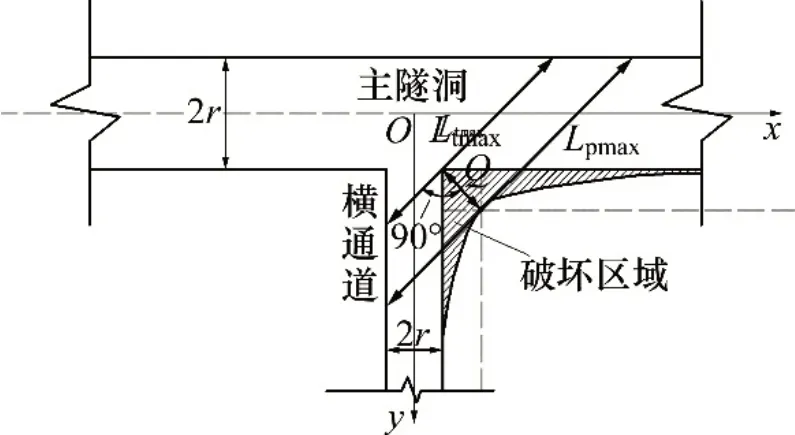
圖7 隧洞三岔口區跨度示意圖Fig.7 Schematic diagram of span of the tunnel

由隧洞三岔口處的幾何關系可得

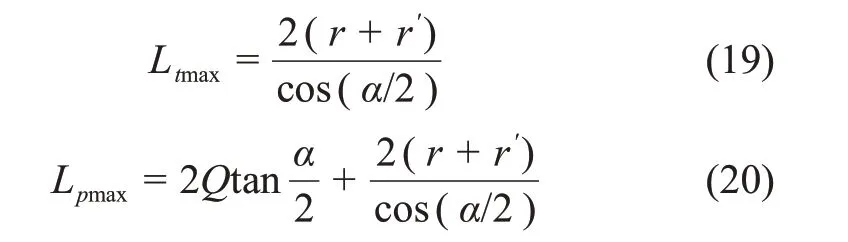
將式(18)代入式(20)可得:

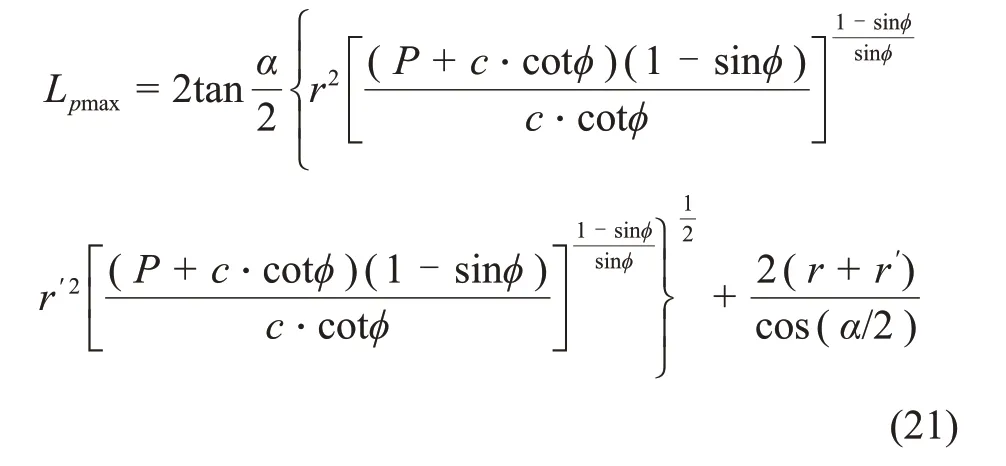
等效跨度值作為隧洞三岔口區圍巖變形位移參數，可反映圍巖穩定性。該值不僅受交叉角α、隧洞尺寸r和r′及破壞深度Q的影響，而且與隧洞埋深H、圍巖力學參數等有關。通過研究發現：當實際修建跨度值L不大于Ltmax時，即L≤Ltmax，三角區圍巖穩定；當遇特殊地質條件時，L會超出Ltmax，但不大于Ltmax，即Ltmax≤L≤Lpmax，此時，需對三角區圍巖進行適當加固；若L≥Lpmax，則三角區圍巖極不穩定，需采取有效加固措施。

3 算例與分析

以貴陽市軌道交通2號線區間為例，全區間采用礦山法，隧洞為雙洞單線馬蹄形斷面結構，采用復合式襯砌，最大埋深53.2 m。為計算簡便，取巖體容重γ=19 kN/m3，隧洞埋深H=50 m，將該隧洞主洞、輔洞分別假定為半徑r=5.0 m，r′= 4.0 m的圓形隧洞。

3.1 隧洞三角區垂直應力分析

1)當R0→∞，得

隧洞三角區圍巖垂直應力僅與隧洞上部巖體容重及隧洞埋深有關。

2)當R0為5r，4r，3r和2r時，分別得式(23)，(24)，(25)和(26)：

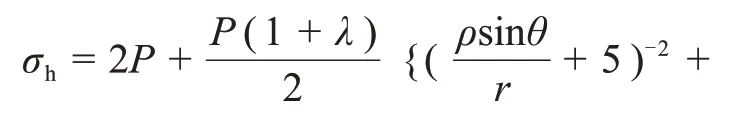
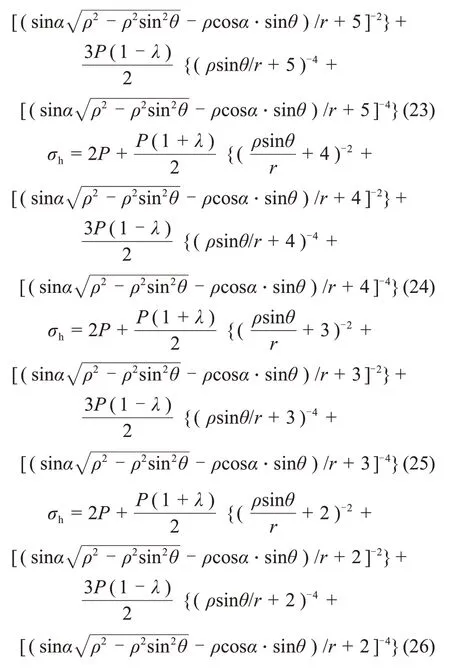
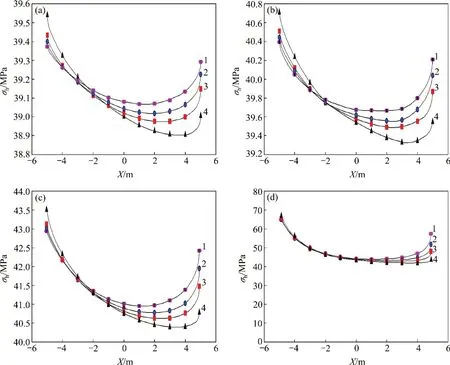
圖8 不同R0下三角區垂直應力分布Fig.8 Vertical stress distribution of lower triangular region in different R0

取側壓力系數λ=0.5，α分別為30°，45°，60°和90°時，由式(22)～(26)分別得σh的分布曲線。圖8所示為不同塑性圈下三角區垂直應力分布圖。由圖8可見：隨著X逐漸減小，圍巖所受垂直應力也逐漸減小；隨著α逐漸減小，三角區兩側的圍巖應力差值變小，隧道結構更穩定；當α=30°時，三角區所受峰值應力最小，且兩側圍巖垂直應力差值最小，三角區圍巖較為穩定，開挖條件較好；當α=90°時，三角區所受峰值應力最大，且兩側圍巖垂直應力差值最大，三角區圍巖極不穩定，此種開挖方案安全風險極高；隨著R0減小，σh逐漸增大，且三角區兩側σh差值逐漸增大，不利于隧道穩定。故需通過圍巖力學參數確定塑性圈范圍，根據垂直應力對隧洞三岔口區進行合理加固與開挖。

為進一步驗證本文理論解析的可行性，現用ANSYS有限元軟件對輔洞與主洞交叉角呈45°時的算例進行數值模擬計算，其網格劃分如圖10所示。

取α=45°，λ=0.5，三岔口區處于Ⅲ級圍巖中，數值模擬結果、解析計算結果如表1所示。由表1可見：1)解析計算和數值計算三岔口區圍巖垂直應力最大值間存在的最大誤差僅為3.92%；2)在同種工況下2種計算方法的結果存在微小誤差，原因在于理論解計算結果為確定值，而數值解則是近似運算的結果，且2種方法的計算假定條件存在差異；3)理論解與數值解間的計算結果十分接近，驗證了本文解析法在三岔口區圍巖穩定性計算中的可行性和準確性。

3.2 隧洞三角區應力集中分析

圖11所示為三岔口應力集中系數等值線分布圖。由圖11可見：越靠近圍巖三岔口交叉點，圍巖應力集中系數越大，三角區域最外圍的應力集中系數最小。這是由于隧洞開挖過程中三角區域外圍巖體容易破壞，在其表面形成卸壓區，為給橫通道與主洞交叉處的頂板提供足夠支撐力，有效支撐區將會向巖體深部轉移，故而應力集中減弱。在實際工程中，一般會將輔洞與隧洞主洞交叉處的尖角部分去掉修建成曲線狀，該過渡曲線應不越過K等值曲線，且與其彎曲程度相似，最好與等值曲線重合。

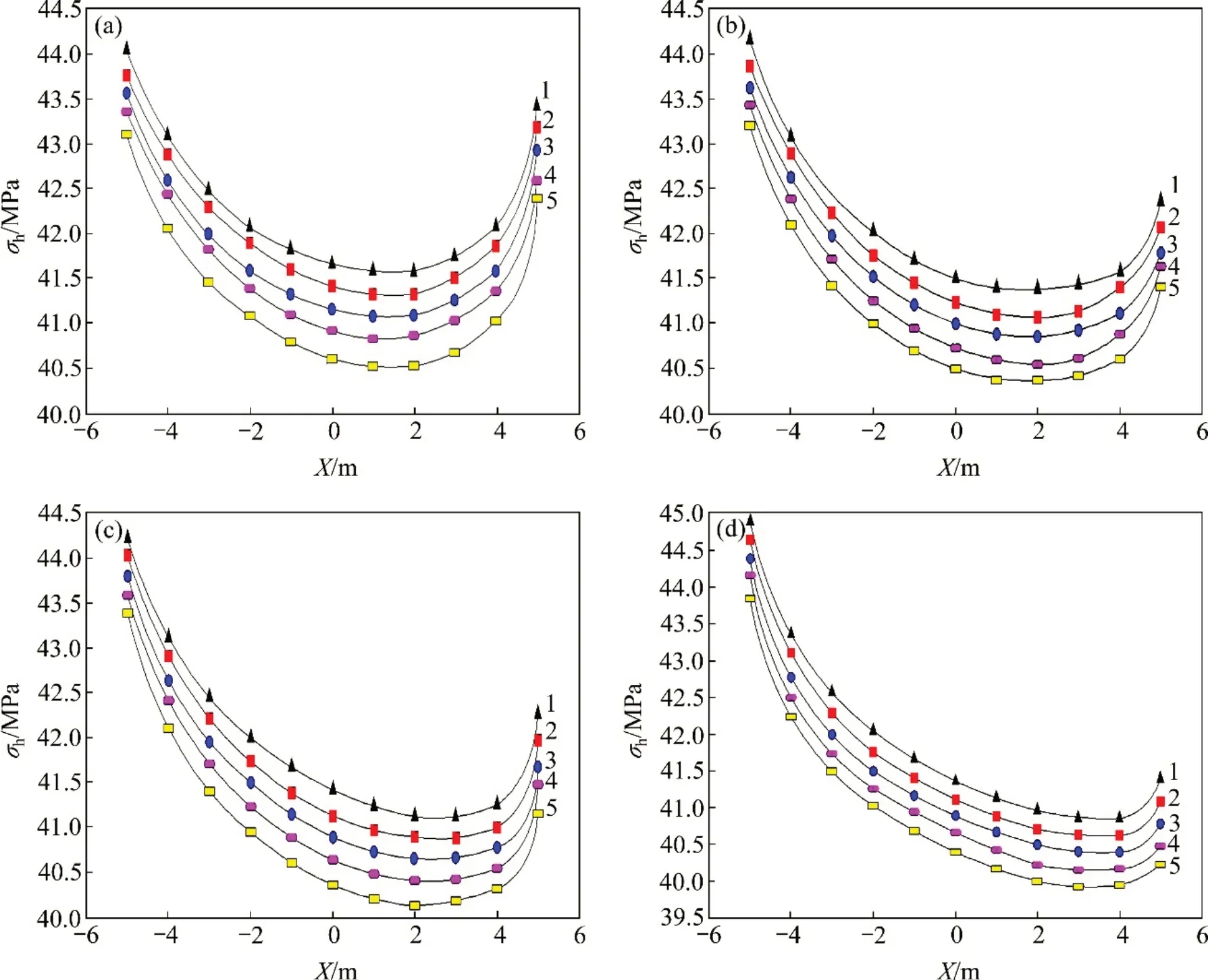
圖9 不同α下三角區垂直應力分布圖Fig.9 Vertical stress distribution in different α lower triangular region

圖10 ANSYS有限元計算網格劃分圖Fig.10 ANSYS finite element calculation grid division diagram

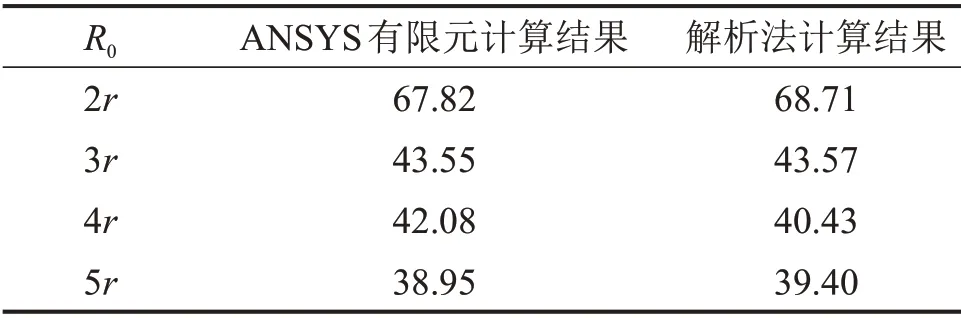
表1 輔洞與主洞夾角為45°三岔口區圍巖垂直應力最大值Table1 Maximum value of vertical stress of surrounding rock in divergence area when the angle between the auxiliary hole and the main hole is 45° /MPa

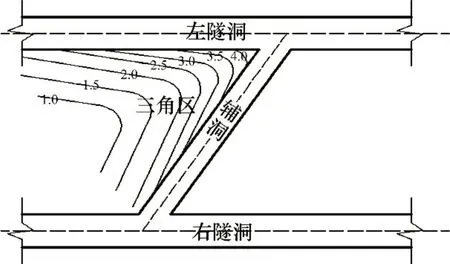
圖11 三岔口應力集中系數等值線分布圖Fig.11 Contour map of stress concentration factor of divergence

由式(11)可知：影響應力集中系數的主要因素有λ，r，R0及α。其中λ和R0是由隧洞所處地理位置決定，針對不同用途r也有相應固定標準，在實際工程中，α的隨機性較大。

當λ取0.5，R0取3r，r取5 m，代入式(11)后得：

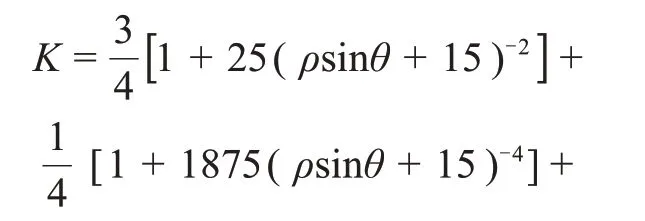
由式(27)繪制不同α下的K曲線，如圖12所示。由圖12可見：隨著α的增大，K的峰值逐漸變大，當α=90°時，K的峰值最大。此時三角區應力高度集中，圍巖穩定性差，不宜于開挖。故而輔助坑道進入隧洞時需以一定角度進入，避免正交方式。

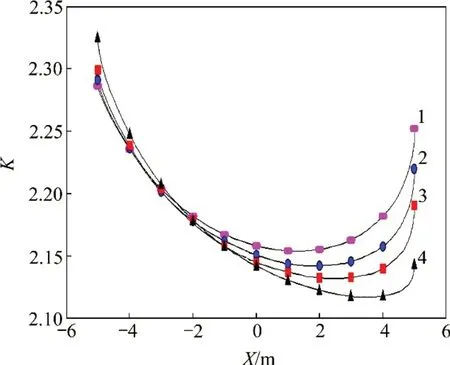
圖12 應力集中系數曲線圖Fig.12 Curves of stress concentration factor

3.3 隧洞三角區破壞深度分析

表2所示為不同圍巖級別下摩擦角φ和黏聚力c。隨著圍巖等級降低，巖體摩擦角φ和黏聚力c逐漸減小。不同等級圍巖過渡轉換時，可根據隧洞三角區最大破壞深度理論計算值，對其加固進行合理化建議。

由式(18)可計算不同圍巖級別下隧洞三角區最大破壞深度。圖13所示為圍巖破壞深度曲線圖。由圖13可見：隨著圍巖等級降低，破壞深度逐漸增加，Ⅰ至Ⅳ級圍巖三角區破壞深度遞增趨勢不明顯，Ⅴ級圍巖中破壞深度層指數形式增加，圍巖級別越差，三角區破壞深度越深。另外，在圍巖等級過渡段，其破壞深度會發生突變，故在圍巖不均勻地段開挖時，需考慮應力突變的狀況；在圍巖過渡段設計、施工時，需設置一定的安全系數。

3.4 隧洞三角區等效跨度分析

圖14(a)所示是由式(19)繪制的α與Ltmax的關系曲線。由圖14(a)可見：隨α增大，Ltmax單調遞增，當α=90°時，Ltmax達到最大值，Ltmax曲線下方為隧洞開挖安全區。

太湖新城地下空間工程位于太湖新城核心啟動區地下，項目總建筑面積30萬m2，占地面積6.8萬m2，地下共3層，結合地鐵4號線支線溪霞路站沿中軸大道南北向布置。地下1層為商業及公共配套設施，設置大量下沉式廣場，進行地面地下交通轉換。地下2層和3層為公共停車空間，共20萬m2，可容納停車2 800輛。該項目計劃于2013年12月開工建設。

令最大破壞深度Q=5 m，圖14(b)所示是由式(20)繪制的α與Lpmax關系曲線。由圖14(b)可見：隨α增大，Lpmax單調遞增，當α=90°時，Lpmax達到最大值。當遇特殊情況時，開挖等效跨度可適當增加，但也不能超過Lpmax曲線的范圍。Ltmax曲線下方為開挖安全區，Lpmax曲線與Ltmax曲線之間為開挖極限區。

當輔洞與隧洞主洞交角α=90°時，得：

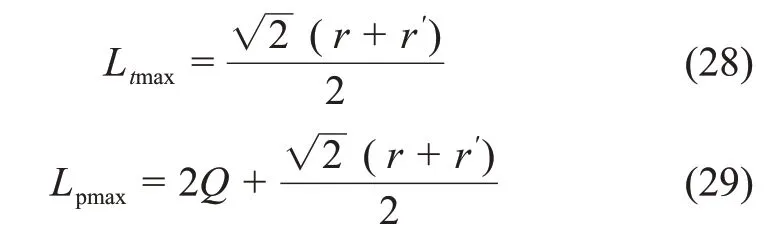
將式(18)代入式(29)得：

圖14 交叉角（α）與等效跨度的關系曲線Fig.14 Cross angle(α)and equivalent span relationship curve

由式(19)和(20)可知，當輔洞與隧洞主洞交角一定時，理論最大等效跨度僅與隧洞尺寸有關，極限等效跨度還與最大破壞深度有關。在設計輔洞進入主洞區時，實際修建跨度應小于理論最大等效跨度，在特殊條件下也不能大于極限等效跨度。

4 結論

1)當α=90°時，圍巖垂直應力最大，隨著α和λ減小，σh減小；隨著R0減小，σh逐漸增大。已知圍巖力學參數、地勘參數，就可根據理論公式對隧洞三岔口區圍巖進行合理加固。

2)在隧洞開挖過程中，越靠近圍巖三岔口的交叉點K越大，三角區域最外圍的K最小，且隨著α的增大，K逐漸變大，當α=90°時，K達到最大值。

3)隨著圍巖等級的降低，破壞深度越大，Ⅰ～Ⅳ級圍巖三角區破壞深度遞增趨勢不明顯，Ⅴ級圍巖中破壞深度呈指數形式增加。

4)隧洞三角區的集中應力大于圍巖極限強度時，圍巖會發生塑性屈服破壞，失去支承能力，在無支護條件下隧洞頂板將會進入小變形階段，甚至進入大變形失穩破壞階段。

5)當α一定時，Ltmax僅與隧洞尺寸有關，Lpmax還與最大破壞深度有關。在設計輔洞進入主洞區時，L應小于Ltmax，在特殊條件下也不能大于Lpmax。