溶液預凍方式與冰晶粒度分布之間的關系

賈穎姣，余云霞，劉志強，羅春

(1.中南大學能源科學與工程學院，湖南長沙，410083；2.新奧泛能網絡科技有限公司，北京，100176)

真空冷凍干燥是一種穩定的干燥過程。其原理如下：通過低溫冷凍使液態水凍結為固態冰，在一定的真空度下，固態水可以直接變為水蒸氣，在真空環境中相應的溫度和氣壓下對物料進行冷凍干燥處理。通過真空冷凍干燥得到的產品具有復水性好、穩定性高以及方便運輸、能長期保存等優點，因此，廣泛應用于真空冷凍干燥技術廣泛應用于醫藥、食品、材料等領域，但由于該技術存在干燥時間長、能耗大等缺點，因而其推廣受到限制。為了減少干燥時間，降低操作成本，得到高質量的凍干產品，必須對最佳凍干工藝條件進行研究[1-5]，但所需試驗量大、成本高，且結果對整個過程的優化缺乏預測性。從機理方面，凍干過程中升華干燥階段耗時最長，而預凍階段影響凍結體的結晶情況即干燥階段的孔隙結構，對凍干過程產生決定性影響。NAKAGAWA 等[6-8]通過模擬得到了凍干速率和成核溫度對冰晶尺寸等參數的影響；賈穎姣等[9]針對液態物料提出了3 種凍結方式，并得出了不同凍結方式對預凍溶液冰晶粒度分布規律的影響。為了提高凍干效率，需要定量地得出不同凍結方式下形成冰晶粒度的分布情況，以及不同冰晶粒度對凍干速率、能耗和復水性等參數的影響，從而獲得凍結條件與凍干效率和產品質量的對應情況，再通過逆向推理從機理上求得最佳凍干曲線。為此，本文作者基于數值模擬針對不同凍結方式與結晶粒度平均值和均勻度之間的函數關系進行研究，以便根據凍結方式預測其粒度分布，并根據干燥階段的需要來調控預凍條件，為研究凍干過程中預凍階段和干燥過程之間的關系提供依據。

1 數值模擬

1.1 物理模型

基于凍干箱內擱板凍結的預凍方式，以凍干機中2 塊擱板間1 個西林瓶內溶液和它所分配的周圍空間作為研究對象，忽略西林瓶液面以上的瓶身和瓶口部分對換熱造成的影響。簡化后的物理模型如圖1所示。

1.2 數學模型

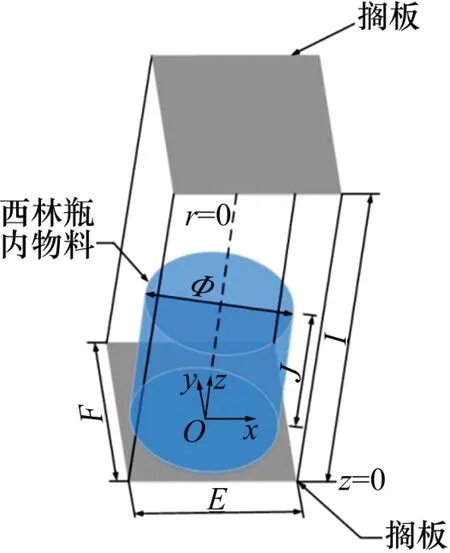
圖1 西林瓶裝物料預凍模型示意圖Fig.1 Schematic diagram of freezing material model in vial

在溶液的凍結過程中，固液相變界面隨著時間的變化而移動，稱為三維兩相stefan 問題[10-13]。針對該物理模型進行如下假設：1)只發生熱傳遞，忽略質傳遞，且傳熱方式為導熱，忽略熱輻射和熱對流；2)忽略固相和液相的密度差異性，即冷凍前后溶液體積不變；3)凍結過程只發生在固液相界面上，其溫度在固化溫度和液化溫度之間，瓶內冰晶為異質成核，不存在過冷情況；4)凍結區域和液相區域各自分布均勻且內部各處物性分別一致，忽略包含的不凝性氣體；5)預凍后只有晶態，沒有形成玻璃態物質。針對相變潛熱的問題，采取多孔-焓法[14-16]來解決，其中，液相的體積分數由熱焓平衡法[17]通過計算得出。能量方程如下：

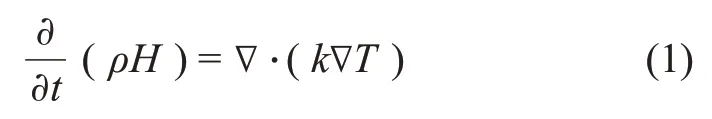
式中：ρ為材料密度，kg/m3；k為導熱系數，W/(m2?K)；T為物料溫度，K；H為材料的焓，J。H由顯焓h和潛熱ΔH之和所得：

其中：href為參考焓，J/kg；Tref為參考溫度，K；比定壓熱容cp定義為

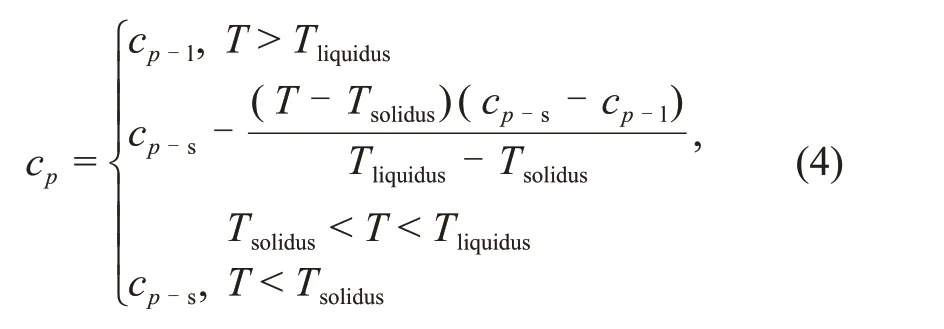
式中：cp-s和cp-l分別為固相和液相的比定壓熱容，J/(kg?K)；Tsolidus和Tliquidus分別為固化溫度和液化溫度，K，糊化區域的溫度介于這兩者之間。

已釋放的潛熱ΔH為溶液單位潛熱L的函數：

其中：ΔH在0～L之間變化；β為液相質量分數，

邊界條件為：

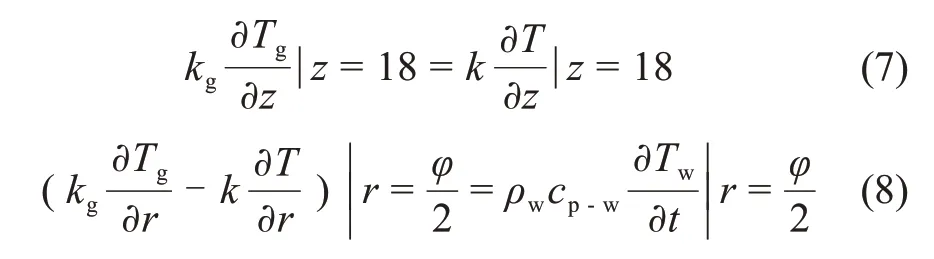
式中：kg為空氣導熱系數，W/(m2?K)；ρw為西林瓶壁材料的密度，kg/m3；cp-w為西林瓶壁的比定壓熱容，J/(kg?K)；Tw為西林瓶壁的溫度，K；Tg為空氣側的溫度，K。

1.3 數值解法

運用Ansys ICEM 軟件建模并劃分網格，且進行網格無關性驗證[9]。導入Ansys Fluent 15.0 軟件，選取凝固和熔化(融化)模型，采用有限體積法的二階迎風格式對控制方程進行空間離散化，殘差設置為10-6，運用SIMPLE 算法對模型溫度進行求解。將所得溫度場變化的數據導入Matlab軟件計算冰晶粒度，并針對該方法進行模型驗證[9]。粒晶顆粒粒度計算公式[6]為

式中：D為冰晶顆粒粒度，μm；c為常數；R為相界面的移動速率，mm/s；G為凍結區域的溫度梯度，K/mm；R和G為通過處理數值計算結果即溫度場間接得到，詳細計算過程見文獻[9]。

關于冰晶粒度的分布，本文選擇平均值和標準差2個參數進行研究，計算式如下：

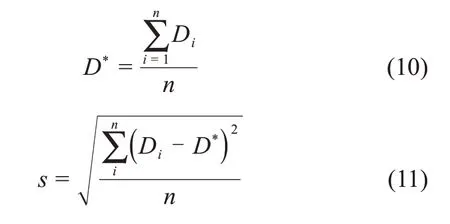
式中：D*為西林瓶中冰晶粒度平均值，μm；n為參考冰晶粒度的位置個數；s為冰晶粒度分布標準差，μm。

1.4 計算參數

1.4.1 幾何模型

甘露醇學名為己六醇，常被用作凍干藥品的低溫保護劑和賦形劑[5,18-19]。本文選取體積分數為10%甘露醇為研究對象，其對應圖1中的幾何尺寸如表1所示。

表1 幾何模型尺寸Table1 Geometric model mm

1.4.2 模擬工況

選取擱板溫度作為預凍過程中的控制變量，分別采用以下3組不同的凍結方式：1)將常溫物料放入溫度恒定的擱板上進行預凍(以下簡稱恒溫條件)；2)先將物料放入常溫凍干箱內，然后控制擱板溫度以一定速率下降直至凍結(以下簡稱恒溫降條件)；3)先使擱板溫度由常溫按照一定的速度下降至養晶溫度Tm并維持一段時間，而后繼續以同樣的速度降溫(以下簡稱混養晶條件)。具體模擬工況如表2所示，這3種凍結方式都在常壓環境下進行。

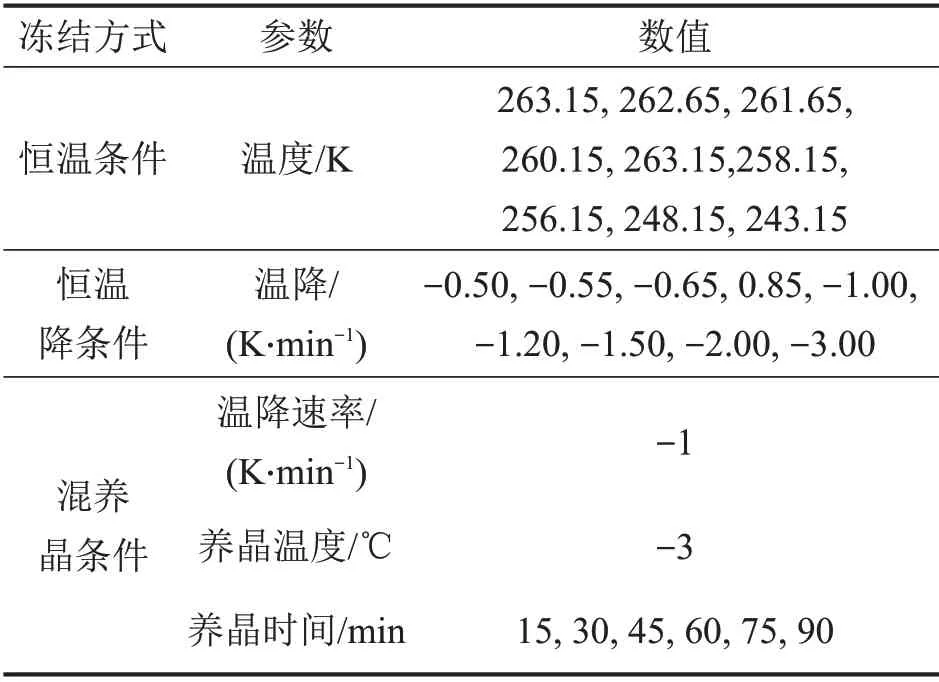
表2 3種不同凍結方式下的模擬工況Table2 Simulation conditions of three different freezing modes

2 關系式回歸研究

2.1 恒溫預凍方式

在恒溫凍結方式下，模擬得出各設定溫度下冰晶粒度的平均值和標準差，結果如圖2所示。為了明確擱板溫度與平均粒度和標準差之間的關系，進行多項式回歸擬合，擬合的多項式為

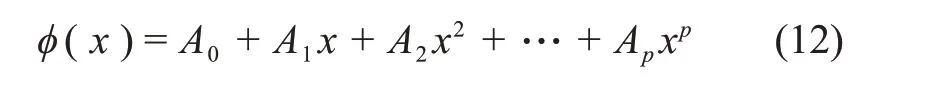
式中：A0，A1，…，Ap分別為該函數中的待定系數；p為待定系數個數；?(x)為擬合得出的冰晶粒度分布參數，即平均值或標準差；x為自變量，即擱板溫度。

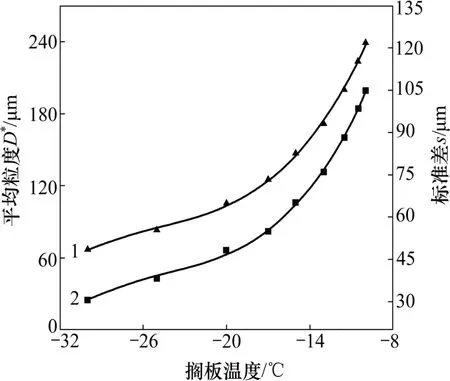
圖2 恒溫預凍方式擬合曲線Fig.2 Fitting curves in constant temperature condition

令

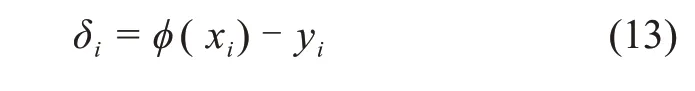
式中：yi為真實的冰晶粒度分布參數；δi為殘量，表示擬合的誤差。按照最小二乘法準則[20]確定系數Ai，即求得使殘量?i平方和最小的Ai。平方和S為

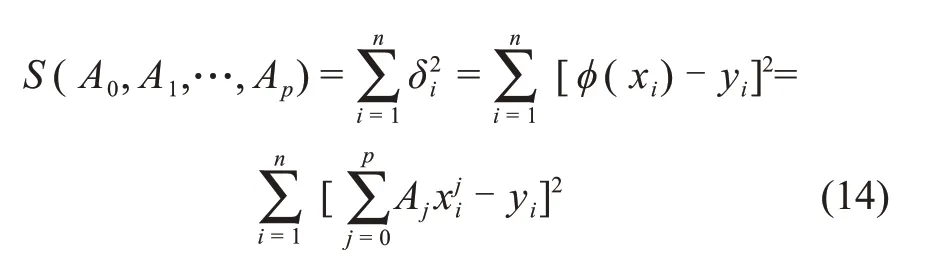
式中：S為殘量平方和。

聯立并求解式(10)和(12)便可求得擬合多項式。分析對比2 次、3 次和4 次多項式的不確定度，選擇最佳擬合多項式，可得擱板溫度-平均粒度的擬合多項式為

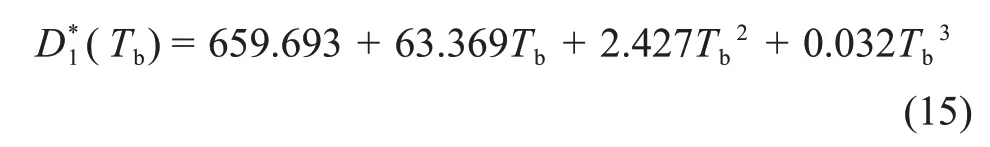
式中：D*1為擱板恒溫凍結方式下擬合得到的冰晶粒度平均值，μm；Tb為擱板恒定溫度，K。

所得擱板溫度-標準差多項式為

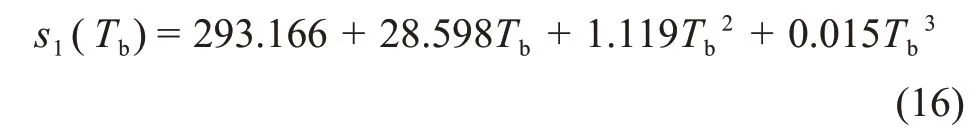
式中：s1為擱板恒溫凍結方式下得到的冰晶粒度分布標準差，μm。擱板溫度-平均粒度擬合曲線與擱板溫度-標準差擬合曲線如圖2所示。

2.2 恒溫降預凍方式

在恒溫降條件下，模擬各設定溫降速率條件下冰晶粒度的平均值和標準差，結果如圖3所示。根據同樣步驟進行多項式擬合，通過不確定度選擇最佳擬合多項式，得溫降速率-平均粒度的擬合多項式為

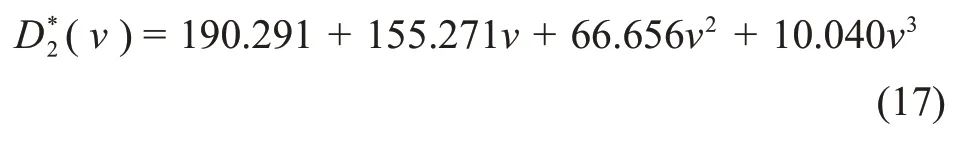
式中：D*2為恒溫降凍結方式下擬合得到的冰晶粒度平均值，μm；v為擱板降溫速率，K/s。所得的溫降速率-標準差擬合多項式為

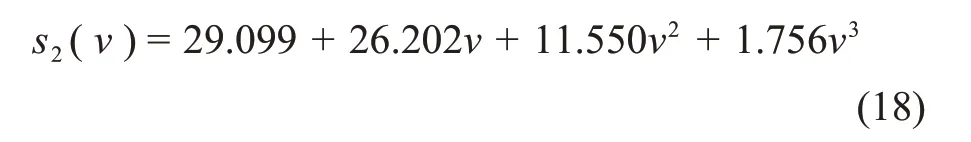
式中：s2為恒溫降預凍結方式下擬合得到的冰晶粒度分布標準差，μm。

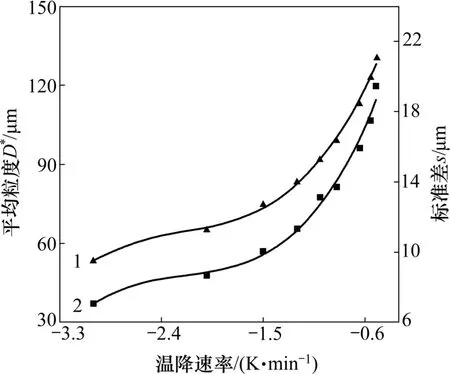
圖3 恒溫降預凍方式擬合曲線Fig.3 Fitting curves in constant temperature condition drop

2.3 混養晶預凍方式

在混養晶條件下，模擬出各設定養晶溫度條件下冰晶粒度的平均值和標準差，結果如圖4所示，可得45 min為粒度分布最均勻的養晶時間。

采用同樣步驟進行多項式擬合，通過不確定度選擇最佳擬合多項式，得養晶時間-平均粒度的擬合多項式為

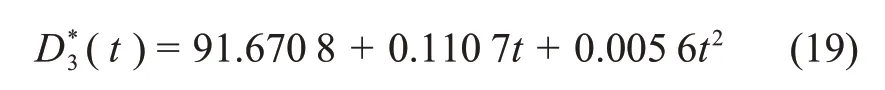
式中：D*3為混養晶預凍方式下擬合得到的冰晶粒度平均值，μm；t為養晶時間，s。所得的養晶時間-標準差擬合多項式為

式中：s3為混養晶預凍方式下擬合得到的冰晶粒度分布標準差，μm。

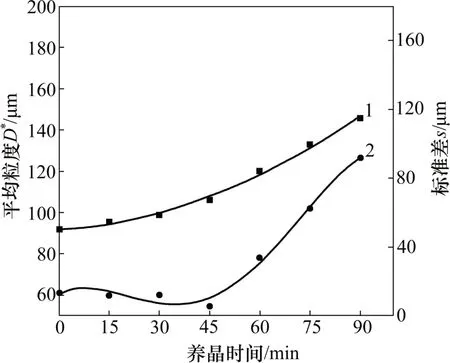
圖4 混養晶預凍方式擬合曲線Fig.4 Fitting curves in crystal growing condition

3 模型檢驗和不確定度分析

3.1 多項式模型的有效檢驗

為了檢驗冰晶粒度和凍結條件之間確實存在多項式關系，需要進行顯著性檢驗，根據多元統計理論，若取Xl=xl，則實際模型的一元多項式非線性回歸問題可簡化為多元線性回歸問題。可根據多元線性回歸的顯著性檢驗統計量檢驗多項式回歸方程的顯著性。

假設H0：A1=0，A2=0，…，Aj=0。

檢驗統計量：

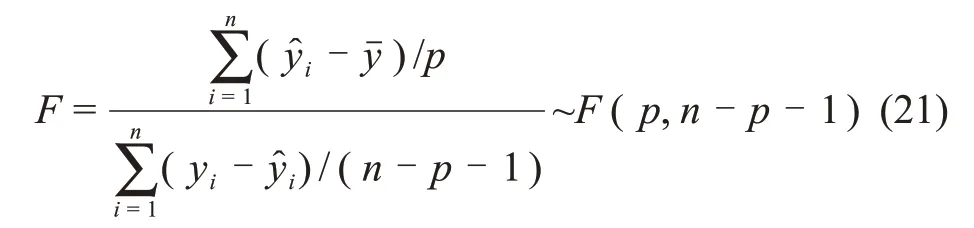
式中：F為檢驗統計量；為由擬合曲線計算的粒徑，μm；yi為由仿真得到的粒徑，μm；為yi的平均值；p為變量的自由度，它與擬合多項式的階數有關，對于多種凍結方式，分別取3，2和4。

若F＞F1-α(p,n-p-1)，則拒絕H0，所得多項式分布在置信水平α上是顯著的。所得結果如表3所示。

3.2 不確定度分析

從3種凍結方式的擬合曲線可以看出，擬合結果與原始結果比較接近，擬合效果較好。

3.2.1 均方根誤差

均方根誤差用來衡量預測值與原始值之間的誤差，在一定程度上反映了所得回歸公式的效果。殘量平方和為

均方根誤差為

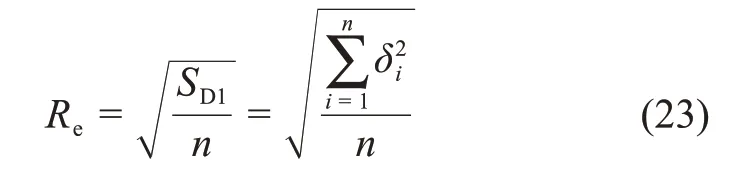
式中：SD1為殘差平方和；δi為擬合誤差，μm。

3.2.2 校正決定系數

雖然均方根誤差可以對擬合進行定量判斷，但均方根誤差也存在一定局限。為了獲得最佳的擬合優度，參考校正決定系數，其值在0～1之間變化，當校正決定系數接近1時，表明擬合效果好。

決定系數R為

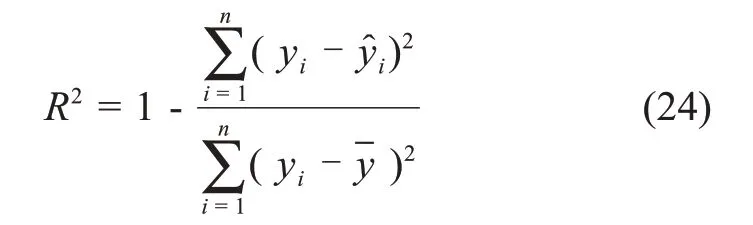
校正決定系數Ra為

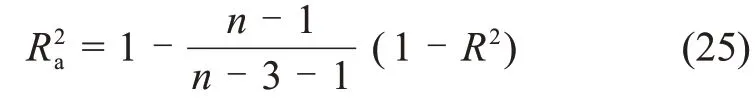
3.2.3 回歸參數標準偏差

標準偏差是用來評定回歸參數的準確度的量。標準偏差越小，則所得參數越準確。

殘余標準偏差se為

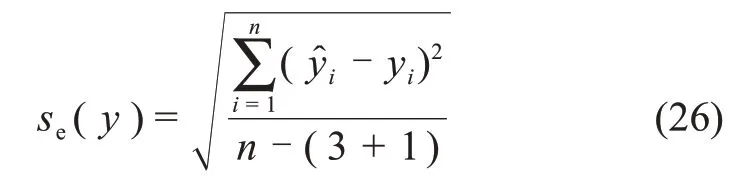
各參數標準偏差se(Ai)(i=1,2,3,4)為

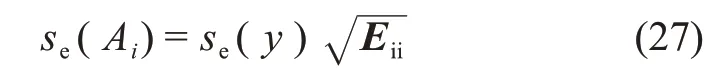
其中：E=B-1；B為求解待定系數Ai的系數矩陣。具體求解過程見文獻[20]；Eii為矩陣E中對應的數值。所得結果如表4所示。

表3 不同預凍條件下擬合多項式顯著性檢驗Table3 Significance test of fitting polynomial under different pre-freezing conditions

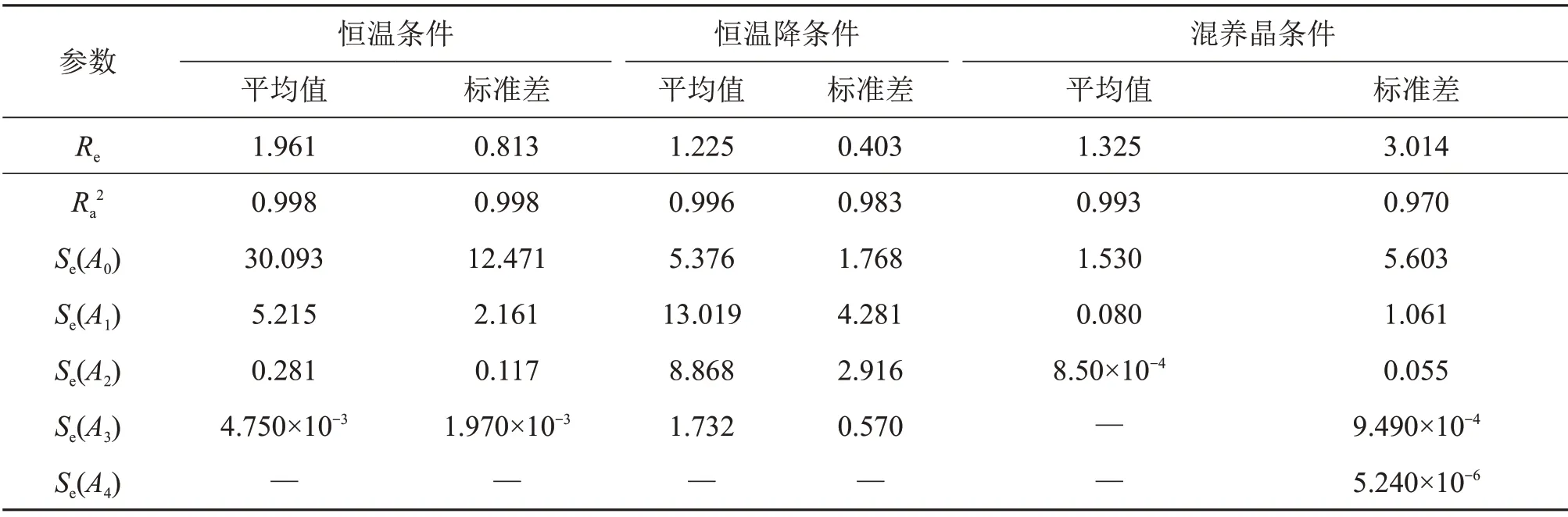
表4 不同預凍條件下擬合多項式的不確定度Table4 Uncertainties of fitting polynomials under different pre-freezing conditions

4 結論

1)在擱板溫度恒定的凍結方式下，擱板溫度-平均粒徑與擱板溫度-標準差之間的回歸關系式均為三次項式；在降溫速率恒定的凍結方式下，溫降溫度-平均粒徑與溫降速率回歸關系式均為三次多項式。而在含養晶過程的恒溫降過程中，養晶時間-平均粒徑關系式為二次多項式，而養晶時間-標準差關系式為四次多項式。

2)擬合優度和參數準確度比較高，而且多項式分布顯著性水平在0.99以上。

3)后續研究可根據結果推算到其他預凍條件下的冰晶粒度分布情況，定量研究預凍條件對凍干效率和產品質量的影響，優化凍干曲線。