PCCP管遠場渦流檢測激勵線圈布置方式研究
商 峰1,王 正,董 猛
(1.中國水利水電科學研究院 水電可持續發展研究中心,北京 100038;2.山東科技大學 土木工程與建筑學院,山東 青島 266590)
預應力鋼筒混凝土管(Prestressed Concrete Cylinder Pipe,PCCP)是指在帶鋼筒的混凝土管芯上螺旋均勻纏繞預應力高強鋼絲,并覆蓋砂漿保護層而制成的管道,在國內外長距離調水工程中廣泛應用。但隨著PCCP管服役時間的增加,PCCP管內的預應力鋼絲會發生斷裂;鋼絲斷裂數量增加到一定程度,就有可能引發爆管。為了保障供水安全,需要研發從PCCP管內定位斷絲區域的無損檢測技術。北美地區由于PCCP管應用歷史較長,因而PCCP管斷絲檢測技術發展較為成熟;國內相關研究近年來剛剛起步。研究表明[1],遠場渦流(Remote Field Eddy Current,RFEC)檢測是用于PCCP管斷絲檢測的重要方法。
遠場渦流檢測和漏磁檢測是常用于鐵磁性管道的無損檢測方法,漏磁檢測信號受溫度影響較大[2],而遠場渦流能夠以同樣的靈敏度檢測管壁上的缺陷,并且不受集膚深度的限制。該技術在油井套管、城市煤氣管道、核反應堆壓力管等管道檢測方面取得了較多的應用。典型的遠場渦流檢測裝置包括一個與管道同軸放置的激勵線圈和若干相距2~3倍管道直徑外的檢測線圈或者磁場檢測傳感器[3-4]。然而,這種裝置一般適用于口徑較小的管道(一般不大于500 mm);對于PCCP管而言,管徑最小為400 mm,最大可達到4000 mm以上[5],如果激勵線圈仍然采用與管道同軸布置的方式,會出現線圈尺寸和激勵電壓過大、線圈難以移動等問題。因此,有必要研發適用于大口徑PCCP管的遠場渦流檢測技術。
數值仿真是研究遠場渦流檢測方法的重要工具。1987年,Lord和孫雨施[6]合作應用有限元方法模擬了遠場渦流中電磁場分布,從中發現了“勢谷”和“相位節”現象。早期,受限于計算機的計算能力,大部分學者都采用軸對稱有限元方法,僅能模擬周向缺陷;研究軸向缺陷需要采用三維有限元[7]。為了簡化計算,部分學者[8]采用全域軸對稱+局部三維的有限元仿真方法,軸對稱仿真的計算結果作為局部三維仿真的邊界條件。隨著計算機軟硬件的發展,全域采用三維有限元仿真成為可能[9]。為能較好地指導實驗,王亞午等人通過模擬發現傳感器的移動速度應控制在2 m/s以內[10]。對于PCCP管討論激勵線圈的布置方式,則需要采用三維有限元方法。
因此,本文即嘗試應用三維有限元方法模擬低頻電磁場在PCCP管壁內外的傳播過程,研究激勵線圈在管壁內的布設方式,為研發相關檢測裝備提供依據。
1 三維電磁場有限元方法
有限元的運用不僅可以形象地描繪出管道內外的磁場分布情況,而且依據仿真計算結果,可以對檢測裝置的設計提供有效的理論指導,并為管道缺陷反演和定量識別提供有力的證據。遠場渦流現象為低頻電磁場現象,以穩態特性為主,可以忽略諧波、檢測速度、磁滯以及位移電流的影響。因此,麥克斯韋方程組可以簡化為[11]
▽×H=Js+Je, ▽×E=-jωB
(1)
▽·B=0, ▽·D=ρ
(2)
式中,Js為激勵線圈中的電流密度;Je為渦流電流密度;B為磁感應強度;H為磁場強度;D為電位移矢量;ρ為體電流密度。在各項同性的導磁管道中,還滿足以下關系:
D=εE,B=μH,Je=σE
(3)
式中,ε為介電常數;μ為磁導率;σ為電導率。為簡化計算,定義矢量磁勢A,▽×A=B,由庫倫規范規定▽·A=0,將其代入式(2)有
▽×(E+jωA)=0
(4)
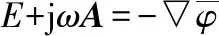
(5)
將式(4)、式(5)和▽×A=B代入式(2)有
(6)
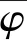
(7)
2 電磁場在預應力鋼筒混凝土管內外的傳播分析
2.1 計算模型
如圖1所示,以內徑為0.4 m的SL型PCCP管為例進行三維仿真分析,管壁結構尺寸參考規范[5]取值。采用ANSYS Maxwell軟件,分析激勵線圈放置在管道不同位置的影響。為優化網格形狀,預應力鋼絲采用等面積的正方形截面進行模擬,有限元網格如圖2所示。由于場量B的變化與接收線圈的電壓成正相關,所以建模時可以不設置檢測線圈。管壁材料參數取值如表1所示。預應力鋼絲斷裂時,依然存在磁導率,但是在斷裂位置附近,沿鋼絲纏繞方向的環形電流將會受阻,因此保持鋼絲單元磁導率不變,將斷裂位置附近鋼絲單元的電導率設為0。激勵源為40 Hz正弦波。
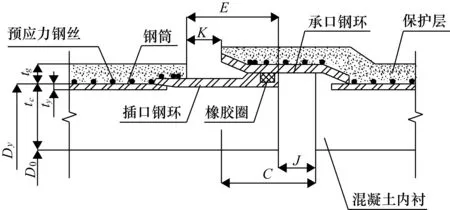
圖1 SL型PCCP管管壁結構圖[5]
遠場渦流有限元分析屬于開放域問題,管外域在管徑3倍處設置索末菲輻射條件[12],此時網格數量為300萬左右。

圖2 SL型PCCP管有限元計算網格
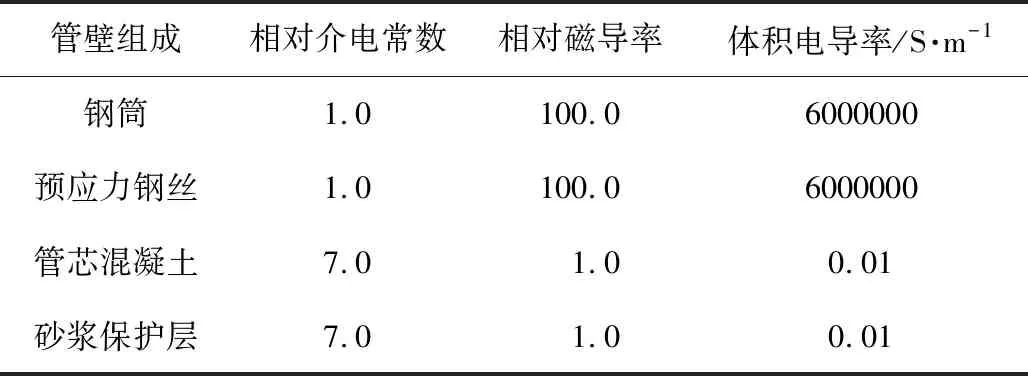
管壁組成相對介電常數相對磁導率體積電導率/S·m-1鋼筒1.0100.06000000預應力鋼絲1.0100.06000000管芯混凝土7.01.00.01砂漿保護層7.01.00.01
2.2 完好管道分析結果
分別計算了3種不同工況:① 激勵線圈尺寸與管徑(d)相近,與管道同軸放置;② 保持激勵電流密度不變,將激勵線圈尺寸縮小到工況1的1/4,與管道同軸放置;③ 保持激勵電流密度不變,激勵線圈尺寸縮小到工況1的1/4,放置在管壁附處。以管軸線方向為z軸,以管徑方向為r軸,取管壁附近點Bz和Br計算結果進行分析。
圖3、圖4給出了上述3種工況下完好管道管壁附近Bz和Br計算分布結果。從圖中可以看到,各工況下,隨著距離增加,近場區(距離激勵線圈2倍管徑以內)Bz和Br幅值衰減較快,遠場區(距離激勵線圈2倍管徑以外)Bz和Br幅值變化趨于平緩。保持激勵電流密度不變,激勵線圈尺寸縮小3/4,遠場區管壁附近磁感應強度減小1~2個數量級;激勵線圈尺寸不變,線圈中心由管軸線遷移到管壁附近時,除靠近激勵線圈附近位置,管壁附近磁感應強度分布差別不大。
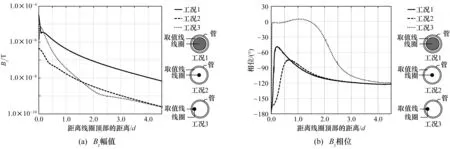
圖3 完好管道Bz計算結果
計算同時表明,近場區3種工況Bz相位差別很大,激勵線圈與管道同軸布置時,Bz相位都是先增加后減小,線圈尺寸越大,Bz相位沿程分布曲線上升段越陡峭;激勵線圈位于管壁附近時,在距離線圈頂端1.5倍管徑距離以內,近場Bz相位接近于0°,1.5倍管徑開始,Bz相位迅速衰減,直到距離激勵線圈3倍以遠,3種工況下Bz相位逐漸趨于一致。激勵線圈與管道同軸放置時,Br相位沒有上升段,相位分布曲線迅速下降后逐漸趨于平緩;縮小線圈尺寸對Br相位影響較小;激勵線圈尺寸不變,線圈中心由管軸線遷移到管壁附近時,Br相位從0.3倍管徑位置即開始迅速衰減,曲線趨于平緩轉折點提前到距激勵線圈約1.5倍管徑位置。
圖5給出了工況3條件下,完好管道管壁附近環向不同角度位置Bz和Br計算分布結果,這里環向角度定義為以管道軸線為圓心、取值線和線圈中心連線對應的圓心角。從圖中可以看到,激勵線圈位于管壁附近位置時,距離線圈0.5倍管徑以遠,不同環向角度位置Bz和Br幅值差別較小;遠場2~4倍管徑之間,環向角度越大,Bz幅值越大,而Br幅值越小。環向角度在90°以內,Bz相位隨軸向距離先增大后減小;環向角度超過90°,Bz相位逐漸轉變為軸向距離單調增加。軸向距離超過3倍管徑,不同環向角度位置Bz相位逐漸趨于一致。Br相位隨軸向距離變化曲線在近場區存在一個緩慢變化的階段,而后急劇減小,再趨于平緩;環向角度越大,緩慢變化段距離越長。
2.3 斷絲管道分析
對距離線圈頂部2.5管徑起斷絲20根的情況進行了仿真分析,分別計算了如下幾種工況:① 激勵線圈尺寸與管徑相近,與管道同軸放置;② 保持激勵電流密度不變,將激勵線圈尺寸縮小到工況1的1/4,與管道同軸放置,斷絲所處截面環向位置與1相同;③ 保持激勵電流密度不變,激勵線圈尺寸縮小到工況1的1/4,放置在管壁附近。在工況3條件下,分別計算了斷絲所處不同環向位置時Bz和Br的分布情況。取管壁附近點Bz和Br計算結果進行分析。
圖6給出了工況1、工況2和工況3-2的計算結果。從圖中可以看到,3種工況條件下,斷絲管道Bz幅值沿程分布與完好管道基本一致,Bz相位沿程分布曲線在斷絲位置略高于完好管道;斷絲管道Br幅值沿程分布曲線在斷絲位置附近略高于完好管道,Br相位在斷絲位置附近呈現倒“N”形分布,與完好管道曲線單調下降的趨勢有顯著區別。
圖7給出了工況3條件下,斷絲管道和完好管道Bz相位差和Br相位差沿程分布情況。可以看到,當激勵線圈位于管壁附近時,遠場Bz相位差呈“幾”形分布,相位差值幾乎不隨斷絲所處的環向位置的改變而改變;遠場Br相位差變化呈現倒“N”形分布,相位差值在斷絲起點(2.5d位置),隨斷絲所處的環向位置的改變而變化顯著。
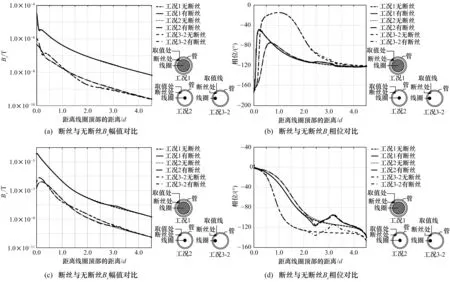
圖6 工況1、工況2和工況3-2斷絲管道計算結果(2.5倍管徑起斷絲20根)
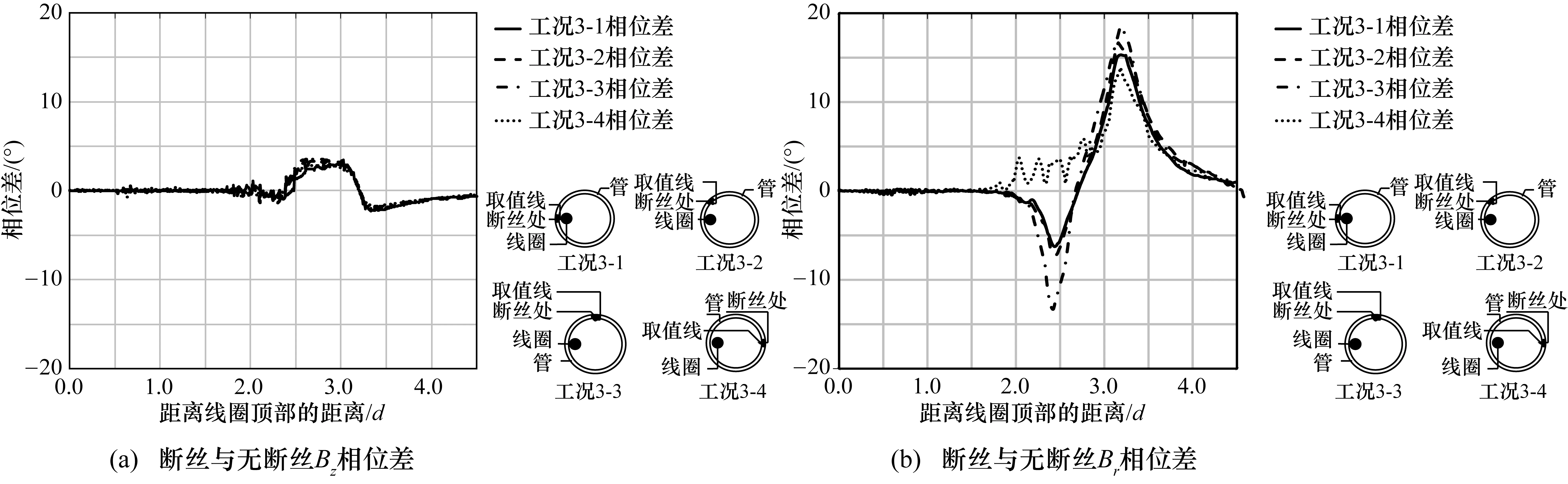
圖7 工況3斷絲管道和完好管道相位差沿程分布(2.5d起斷絲20根)
圖6和圖7的計算結果表明,當激勵線圈布置在管道不同位置時,無論以Br或是Bz作為檢測指標,激勵線圈的位置影響不大;但當激勵線圈布置于管壁附近時,檢測出斷絲的環向位置是可能的,此時,Br相位比Bz相位更適于作為檢測指標。
3 結論
通過應用三維電磁場有限元方法,研究了激勵線圈的布置方式對預應力鋼筒混凝土管斷絲檢測效果的影響,可以得出以下幾點結論:
① 激勵線圈位于管道不同位置時,保持激勵電流密度不變,改變線圈大小和位置,只會改變遠場Bz和Br幅值的分布,不會改變遠場Bz和Br相位的測量效果。
② 激勵線圈置于管壁附近時,遠場Bz相位差在斷絲位置附近呈“幾”形分布,但相位差值幾乎不隨斷絲所處的環向位置的改變而改變;遠場Br相位差在斷絲位置附近呈現倒“N”形分布,但相位差值在斷絲起點,隨斷絲所處的環向位置的改變而變化顯著。因此,
通過檢測管內遠場磁場相位,檢測出斷絲的環向位置是可能的,此時,Br相位比Bz相位更適于作為檢測指標。
③ 本文僅研究了斷絲位置附近的Bz和Br的計算分布,實際檢測中,并不能預先知道斷絲位置的環向角度,因此需要進一步深入研究激勵線圈、斷絲位置、Bz和Br的取值位置(即檢測線圈/傳感器位置)之間的關系對斷絲檢測效果的影響,建立斷絲位置環向角度的檢測定位方法。

