例析特殊值法在中考數學客觀題中的應用

高長亮

(安徽省淮南市民生中學 232000)

由于選擇題和填空題是一類只注重結果而不需要寫出解題過程的特殊問題,根據這一特點,我們可以采用多種方法來解答,通常常用的方法有：直接法、排除法、驗證法、特殊值法等等.本文主要研究特殊值法在客觀題中的應用.由于事物存在特殊性也包含著事物的普遍性,因此在研究某些客觀題時,我們可以不考慮它的一般情況,而假設特殊情況去研究,從而使原問題獲解,這就是所謂的“特殊值法”.用特殊值法探求解題的途徑,可以避免繁瑣的計算和推證,簡便而快捷地求出問題的答案.

具體做題時,當客觀題的結論唯一或題設條件中提供的信息暗示答案是一個定值,而已知條件中含有某些不確定的量時,可以將題中變化的不定量選取一些符合條件的恰當特殊值(或特殊函數,或特殊角,圖形特殊位置,特殊點,特殊方程,特殊模型等)進行處理,從而得出探求的結論.下面結合往年中考數學選擇題或填空題,舉例說明特殊值法在中考數學中的應用.

一、特殊值的應用

例1已知a<0,那么點P(-a2-2,2-a)關于x軸的對稱點是在第____象限．

分析對于大部分學生來說,可以通過a的范圍直接判斷出來點P在第幾象限，從而就可以得出點P關于x軸的對稱點在第幾象限.但是如果我們直接設a是一個滿足條件的簡單的數,判斷起來更方便更準確.

解設a=-1,則P(-3，3)關于x軸的對稱點是(-3，-3)在第三象限，所以點P(-a2-2,2-a)關于x軸的對稱點是在第三象限．

例2無論m為任何實數，二次函數y=x2+(2-m)x+m的圖象都經過的點是____.

分析由題意可知，不論m為任何實數，二次函數y=x2+(2-m)x+m肯定都經過同一個定點.也就是說當m取不同的值時，所有的二次函數都相交于一點,于是我們可以給m賦兩個不同的值，得到兩個不同的二次函數，然后求這兩個二次函數的交點.如果只有一個交點,那么這個交點便是我們所求的定點,如果有兩個交點,我們可以給m再賦一個不同的值,求這個二次函數與前面得到的任一個二次函數的交點,那么兩次求得的公共交點便是所求的定點.學生如果想不到給m賦予特定的值，這一道題就很難思考，不知道從何下手.

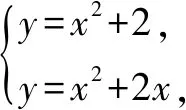
二、特殊點的應用

例3如圖1,點P是ABCD內一點,且S△PAB=5,S△PAD=2,則S△PAC=____.

分析如圖1,已知點P是ABCD內任意一點，△PAB和△PAD的面積分別是5和2,求△PAC的面積,因為這些三角形之間不具有同底等高的一些性質,所以很難直接求出.通過題意我們知道,△PAC的面積應該是一個定值,跟點P在ABCD內的位置無關,因此我們可以將點P特殊化在對角線BD上,如圖2所示,此時就很容易得出S△DAB=S△PAB+S△PAD=7,從而得出S△DAC=7,再根據S△PAD=S△PCD=2,就可以求出S△PAC.

解因為點P是ABCD內任意一點，所以可以將其特殊化在對角線BD上.如圖2所示：

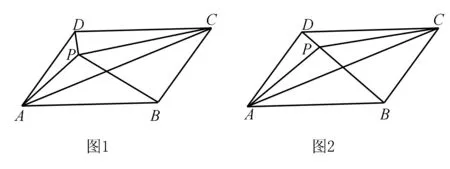
當點P在對角線BD上時，∵S△DAB=S△PAB+S△PAD=7,∴S△DAC=7.

又∵S△PAD=S△PCD=2，∴S△PAC=7-2×2=3.

三、特殊圖形的應用

例4(2009年安徽省中考題)△ABC中,AB=AC,∠A為銳角,CD為AB邊上的高,I為△ACD的內切圓圓心,則∠AIB的度數是( ).

A.120° B.125° C.135° D.150°

分析根據題意,我們可以畫出圖形,如圖3所示,要求∠AIB的度數,需要求出∠DAI和∠ABI的度數和,可是僅僅只根據△ABC是一個等腰三角形,不容易直接求出,如果我們把△ABC特殊化為等邊三角形,如圖4所示,那么問題就變得簡單多了.

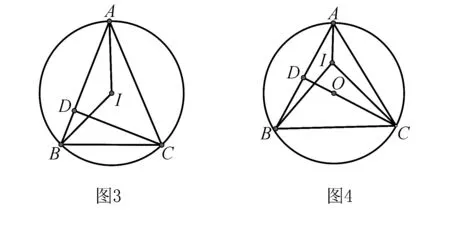
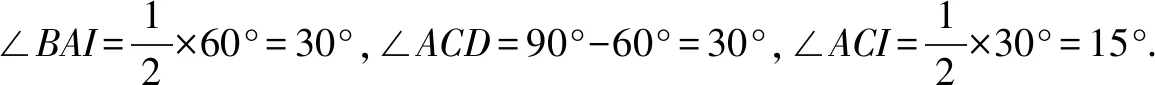
∵△BAI≌△CAI(SAS), ∴∠ABI=∠ACI=15°,

∴∠AIB=180°-30°-15°=135°.

上面通過幾個例題簡單介紹了特殊值法在中考數學客觀題中的應用，我們可以清楚地看到，對于某些較難的客觀題，有時我們利用特殊值法輕松地就可以求出其解.但是需要提醒大家的是：不是所有的客觀題都適用特殊值法，所以一定要認真審題，再根據題的特點決定能否用特殊值法，另外采用特殊值法時，設特殊的值或特殊的點時，一定要在允許的范圍內，否則求出的結果就不符合題意了.