關于一類數列求和的解法探究
張俊暢 楊柳忠
(廣東省大埔縣虎山中學 514299)
求通項為等差數列與等比數列的積的數列的前n項和,是數列求和中的一種重要題型.在教學中,我們發現,此類問題常用錯位相減法解決,解法比較單一,計算量大,合并化簡時,學生很容易搞錯,那么此類問題還有哪些解法,他們各自的優缺點在哪里,怎樣進行合理的選擇等等,此文將對此做些研究.
以2017年天津高考理科數學18題為例:已知{an}為等差數列,前n項和為Sn(n∈N*),{bn}是首項為2的等比數列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(1)求{an}和{bn}的通項公式;
(2)求數列{a2nb2n-1}的前n項和(n∈N*).
分析由題中的條件易求an=3n-2,bn=2n.我們來重點關注第二個問的求法,這里給出兩種不同解法.
一、錯位相減法
解設數列{a2nb2n-1}的前項和為Tn,由a2n=6n-2,b2n-1=2×4n-1,有a2nb2n-1=(3n-1)×4n,故
Tn=2×4+5×42+8×43+…+(3n-1)×4n,
4Tn=2×42+5×43+8×44+…+(3n-4)×4n+(3n-1)×4n+1,
上述兩式相減,得
-3Tn=2×4+3×42+3×43+…+3×4n-(3n-1)×4n+1
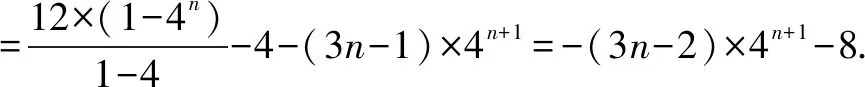
所以,數列{a2nb2n-1}的前項和為
解法提煉錯位相減法求和是求解由等差數列與等比數列的積構成的數列的和的標準解法,主要考查同學們數列公式的掌握程度和數式的運算化簡能力.同學們在錯位相減后用等比數列求和時容易把數列的項數搞錯,還有運算化簡很容易犯錯,這也是這種方法的弊端.
二、公式法
我們發現由等差數列與等比數列的積構成的數列都可化為形如{(an+b)·qn-1}的形式,現在我們來詳細研究此類數列的前n項和Sn的結構特點:
1.問題:設cn=(an+b)·qn-1,求數列的前n項和Sn.
2.猜想:觀察上例,我們不難看到此類數列的前n項和Sn是一次函數與指數函數的乘積與一個常數的和,嘗試幾個例子后,也有相同的結論,那么此類問題的一般結論是什么?它們之間到底存在怎樣的關聯呢?
3.公式推導:記an=an+b,bn=qn-1則
Sn=a1b1+a2b2+…+an-1bn-1+anbn…①,
qSn=a1b2+a2b3+…+an-1bn+anbn+1…②.
由②-①得:
(q-1)Sn=-a1b1-d(b2+b3+…+bn)+anbn+1
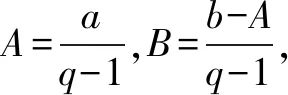
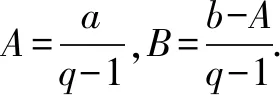
4.結論:形如{(an+b)·qn-1}的數列的前n項和是一次函數與指數函數的乘積減該一次函數的常數項.
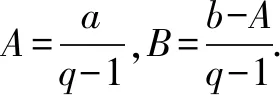
5.應用此結論解上題:
解設數列{a2nb2n-1}的前項和為Tn,由a2n=6n-2,b2n-1=2×4n-1,有a2nb2n-1=(3n-1)×4n.
設{(3n-1)×4n}的前n項和為Tn=(An+B)·4n-B,
則T1=a1=4A+3B=8…①.
∵T2=a1+a2=88,∴T2=32A+15B=88…②.
由①②解得:
也可以這樣解:∵(3n-1)×4n=(12n-4)×4n-1,設其前n項和為Tn=(An+B)·4n-B,
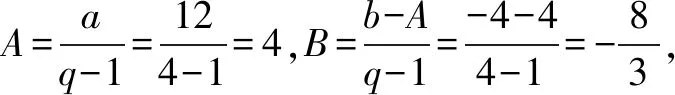
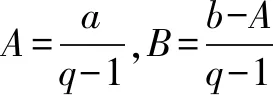
在這里還得說明一下,由于此公式課本上并沒有給出,所以在做解答題時不能直接使用,但我們可以按方法1的步驟求解后,用此法來檢驗最后結果的正誤.當然在做此類問題的選擇填空題上,直接運用公式法,可繞開中間繁瑣的運算化簡的過程,從而快速得出準確的結果,效果會比較好.
巴甫洛夫說過:“復雜現象只是逐步逐段的被科學所認識,但它總是越來越多地逐漸背科學完全掌握.”
我們在數學的學習與實踐中要善于觀察,求同存異,大膽猜想,勇敢探索,逐步逐段的接近真理,直至完全掌握它.這種對學生進行逐次漸進的解題意識和能力的培養,也正是新時期我們教育教學的一個努力方向.

