思維風暴下的“構造之花”
——賦值構造在代數式最值問題中的應用
孫如敏
(江蘇省睢寧縣第一中學 221200)
構造思想的核心是構造,構造是什么?怎么構造?構造作為一種手段,具有十分明確的目的,它與要認識和解決的數學問題緊密聯系著.筆者在講授函數最值時對構造的思想方法頗有感觸,在課堂的教學過程中提出了若干種常規的方法,雖然這些常規手段是我們解決函數最值時的首當其沖應該想到的,不過對于一些頗為棘手的難題,當我們用常規方法不太好解決時,可以根據題目中的條件對目標代數式進行構造,正所謂正難則反,選擇好的構造方法往往讓我們覺得耳目一新.下面就筆者在講授相關最值問題的一些案例和讀者共享.
案例1 設二次函數f(x)=ax2+(2b+1)x-a-2(a,b∈R,a≠0)在[3,4]上至少有一個零點,求a2+b2的最小值.
下面一段文字是筆者對課堂實錄的一部分.
T:二次函數f(x)=ax2+(2b+1)x-a-2(a,b∈R,a≠0)在[3,4]上至少有一個零點,意味著什么呢?
S:意味著此二次函數所對應的圖象在[3,4]這個區間上有一個或者二個交點.
T:能否在演稿紙上把相應的示意圖畫出來呢?
S:(學生默默地拿筆在演稿紙上畫圖,時間大概二三分鐘)……
T:學生把各自作圖成果展示給大家伙看,一起總結分析(教師用投影儀把學生畫的圖展示出來).我們發現滿足題目條件的圖象種類較多,每一種圖象的情況找出相應的限制條件.
S:經過剛才的討論情況,發現滿足條件的二次函數圖象情況較多,每一種情況也相對復雜些,把這么多種情況都考慮全面了,估計將耗費更多的時間和精力.
T:想一想有沒有更加好的辦法呢?
S:難不成我們可以利用條件直接去構造不成?
T:我們可以試試通過參變分離的方式構造出有關a2+b2的方程或者不等式來分析.
S:由已知得,設t為二次函數在[3,4]上的零點,則有at2+(2b+1)t-a-2=0,從而有
at2+2bt+t-a-2=0,即有2-t=[a(t2-1)+2bt].現在只能分離到這一步了,雖然本意想參變分離,但是盡我所能只能分到這一步了.
T:你們已經做得很好了,想徹底地做到參變分離的確有點困難,想想我們還可以通過其它什么方式做到參變分離呢?(留足夠時間思考)
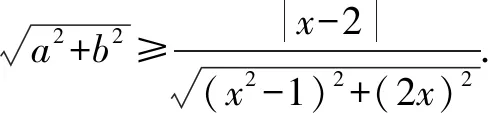
小結:上述案例就是用構造的方式求代數式的最值或者范圍問題,但構造的方式方法是多種多樣的,至于什么樣方式得看具體的條件來處理.有時候當一種方法失敗后就得學會在失敗的基礎上進行反思,不斷修正從而找到正確的構造方法.下面我們再欣賞一個案例:
案例2 設二次函數f(x)=2px2+qx-p+1,當|x|≤1時,f(x)≥0恒成立,求p+q的最大值.
下面一段文字是筆者對課堂實錄的一部分.
S:此題的條件和案例1所給條件從邏輯上講是對立的,但解題的方式恰恰是類似的,都可以從圖象入手,從正面考慮二次函數在區間[-1,1]上圖象永遠在x軸的上方或者在其上方時最多有一個交點,用不等式或者不等式組去限制時情況較復雜,所以也可以和上述案例一樣,采用構造的方式構造出有關p+q的代數式進而求出相應的范圍.
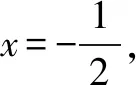
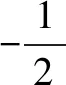

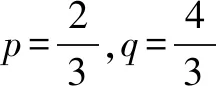
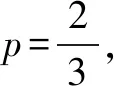
S:這種賦值構造的理由讓人受益匪淺,值得借鑒,對于代數式求最值或者證明其滿足某個范圍的時候,如果從正面考慮比較復雜,正所謂正難則反,通過構造的確是一個不錯的思路,其中賦值構造的辦法讓人眼界大開,很是不錯.
在解題的過程中有些人在達到目標和解答題目方面比較成功,另一些則沒有那么成功,數學教育的成功之處就是在于讓學生在解題的過程中充分體驗各種情緒,如失望,等待,焦慮,恐懼,期望,希望,激動,興奮.在對難度較大的數學題目面前是各種方法的較量與博弈,而在各種方法的博弈中,思維風暴下崩發出的構造之花更是錦上添花!

