提高監控反思 強化邏輯推理
鄭 良
(安徽省靈璧第一中學 234200)
筆者在進行高三二輪“數列”專題復習備課時,遇到了如下兩道試題,很容易就發現了其中的解答錯誤.而類似的運算錯誤在學生答題中比較常見,故撰寫此文,以示提醒,以期拋磚引玉,引發更多、更好的解決方案.
一、試題與解答
例1設等差數列{an}滿足:3a7=5a13,cos2a4-cos2a4sin2a7+sin2a4cos2a7-sin2a4=-cos(a5+a6),公差d∈(-2,0),則數列{an}的前n項和Sn的最大值為( ).
A.100π B.54π C.77π D.300π
解設等差數列{an}的公差為d,由3a7=5a13,得a1=-21d.
cos2a4-cos2a4sin2a7+sin2a4cos2a7-sin2a4=cos2a4(1-sin2a7)-sin2a4(1-cos2a7)=cos2a4cos2a7-sin2a4sin2a7=(cosa4cosa7-sina4sina7)(cosa4cosa7+sina4sina7)=cos(a4+a7)cos(a4-a7)=-cos(a5+a6).
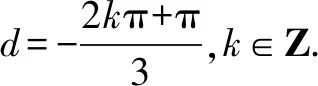
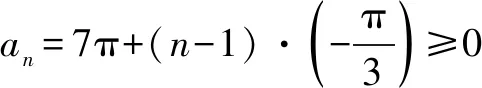
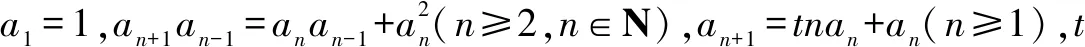
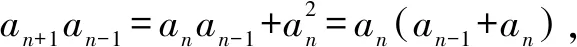
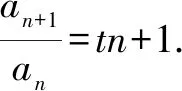
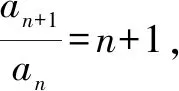
當n≥5時,n!的個位數字為0,而1!+2!+3!+4!的個位數字為3,所以所求前100項和的個位數字也是3.
二、案例剖析
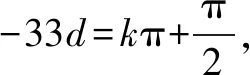
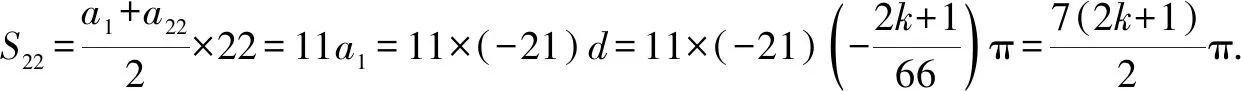
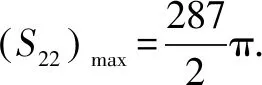
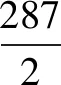
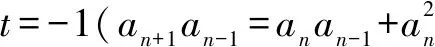
下面分別驗證其充分性:
當t=1時,an+1=(n+1)an,得an≠0,以上解答成立.(或先求an=n!,再驗證滿足an+1an-1=an(an-1+an)),此時所求前100項和的個位數字為3.
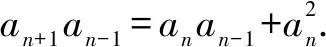
綜上所述,a1+a2+…+a100的個位數是3或1.
三、兩點感悟
1.深化運算能力 提高監控反思
數學運算是指在明晰運算對象的基礎上,依據運算法則解決數學問題的素養.主要包括:理解數學對象,掌握運算法則,探究運算思路,選擇運算方法,設計運算程序,求得運算結果.數學運算主要表現為:理解運算對象,掌握運算法則,探究運算思路,求得運算結果.運算求解能力是指會根據法則、公式進行正確運算、變形和數據處理,能根據問題的條件尋找與設計合理、簡便的運算途徑,能根據要求對數據進行估計和近似計算.運算求解能力是思維能力和運算技能的結合.數學運算是解決數學問題的基本手段,通過運算可以促進學生思維發展,形成規范思考問題的本質,養成一絲不茍、嚴謹求實的科學精神.提高數學運算素養必需夯實基礎知識、通曉運算規則,具有整體意識,明確問題走向,根據不同情形適時調整的能力.
學習過程中,可通過適當的合作學習,培養檢驗意識和技能等方式提高自我監控能力.解決問題時嘗試思考:還有哪些角度?還有哪些方法?方法與結論是否能夠推廣等等.自我監控能力的提高可實現根據具體問題進行自我調節從而保證了學習的效果.學生對除法運算中除數不能為零的元認識知識是具備的,但對其相關的元認知體驗未必深刻,它需要較多的正例與反例的強化與感悟.例1中,在方程cos(a4+a7)cos(a4-a7)=-cos(a4+a7)兩邊同時除以cos(a4+a7)是至精至簡的需要,也是化歸與轉化的體現,但解題者出現了對運算法則理解的 “暫時缺失”從而導致了錯誤操作.
2.強化邏輯推理 規范書寫步驟
邏輯推理是指從一些事實和命題出發,依據規則推出其他命題的素養.邏輯推理是得到數學結論、構建數學體系的重要方式,是數學嚴謹性的基本保證,是人們在數學活動中進行交流的基本思維品質.推理論證講究言必有據,先證后用是解題的基本規范,也是演繹推理的根基.
平時解題的書寫要規范,要寫清問題的原理(數學模型),盡可能做到不跳步.注重論據的落實,形成完整的推理論證鏈.如何求集合A和B的交集A∩B?一般有如下方法:
①平行型.先分別求出集合A,B,再求A∩B;
②遞進型.在集合A(B)的基礎上滿足集合B(A);
③交錯型.對A,B交叉使用,最終確保滿足A,B.