基于干擾觀測器的機械臂改進趨近律的滑模控制
(蘭州交通大學 自動化與電氣工程學院,甘肅 蘭州 730070)
機械臂因其獨特的靈活性,已在農業采摘、安全防爆、醫療衛生等領域得到了普遍的應用,但由于機械臂是一類多輸入多輸出、存在參數不確定性、外界干擾及未建模動態等不確定性的非線性系統,這些因素增加了精確控制的難度[1-2]。因此,提高機械臂控制系統的穩定性和精確性有現實的需求。
滑模變結構方法可以較好地克服系統參數變化以及外界干擾帶來的影響,實現對機械臂的有效控制,但其在控制過程中產生的抖振現象會對機械臂的安全性、穩定性、精確性產生較大影響,因此抖振削弱問題引起眾多學者的關注[3-5]。文獻[6]提出一種改進的冪次趨近律,對其趨近性能進行分析,有效抑制系統抖振,但沒有考慮摩擦與外界干擾的影響。文獻[7]提出一種多冪次滑模趨近律,該趨近律通過3個冪次項系數在系統趨近過程的不同階段進行針對性調節。文獻[8]采用狀態觀測器對系統外部的干擾進行實時估計,利用模糊控制策略對非線性誤差反饋控制加以改進,從而實現誤差反饋增益的優化整定。文獻[9]對引入干擾觀測器的機械臂系統采用滑模反演法設計控制器,提高了跟蹤性能,但設計過程略顯復雜。
本文綜合考慮上述問題,針對存在抖振問題和外部干擾等不確定因素影響下的機械臂軌跡跟蹤控制,提出了一種改進指數趨近律,并將干擾觀測器與滑模控制策略相結合。改進趨近律可以有效削弱抖振;干擾觀測器對系統的不確定因素和外界干擾進行觀測和補償;利用滑模控制器對未觀測到的干擾進行補償。仿真結果驗證了該控制策略的有效性和優越性。
1 機械臂數學建模
由拉格朗日運動學可以建立機械臂的N關節動力學方程:
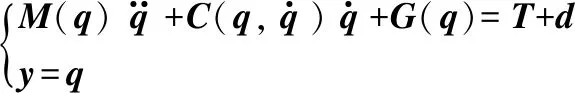
(1)
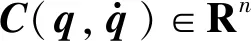
式(1)所描述的機械臂系統具有如下動力學特性。
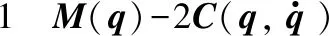
特性2 慣性矩陣M(q)是對稱正定矩陣,其逆M-1(q)存在,并且存在正數m1、m2滿足如下不等式:
m1‖x‖2≤xTM(q)x≤m2‖x‖2
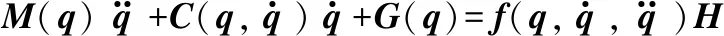

由于系統存在外部干擾信號,在設計過程中為使觀測器能夠較好地跟蹤期望的輸入角度qd,在設計時做出如下假設:
假設1 期望角度qd及其n階導數存在且有界。
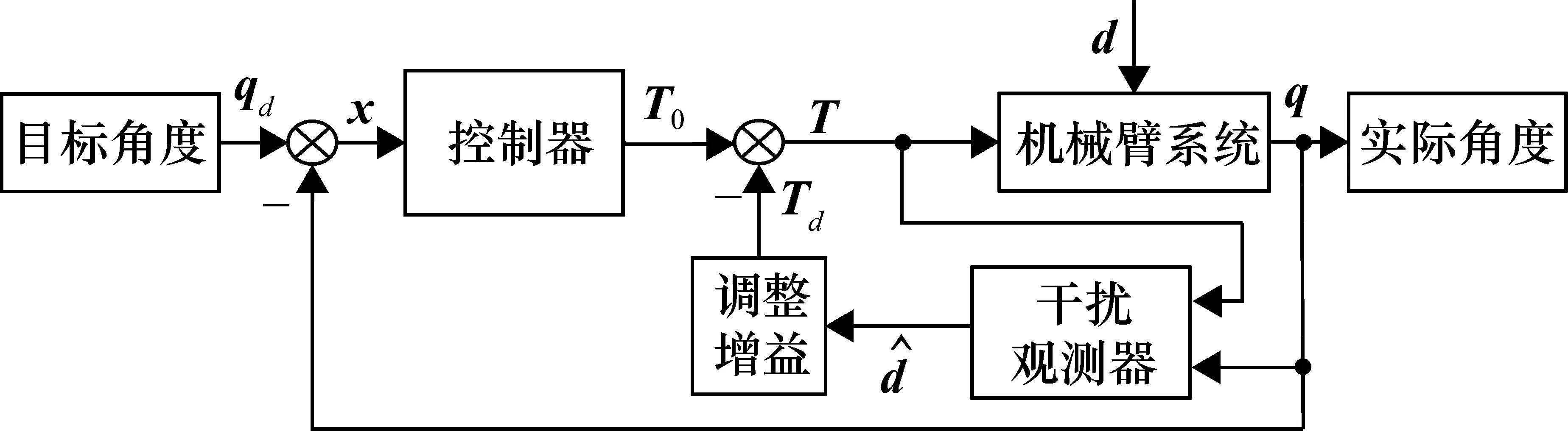
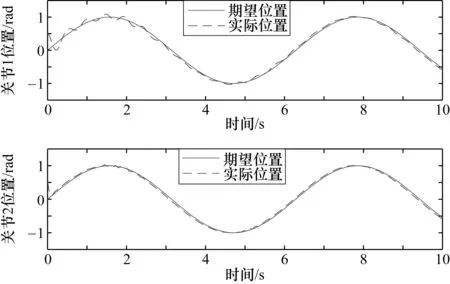
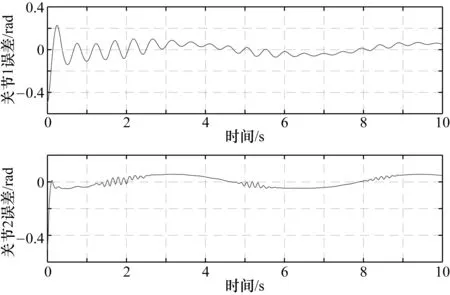
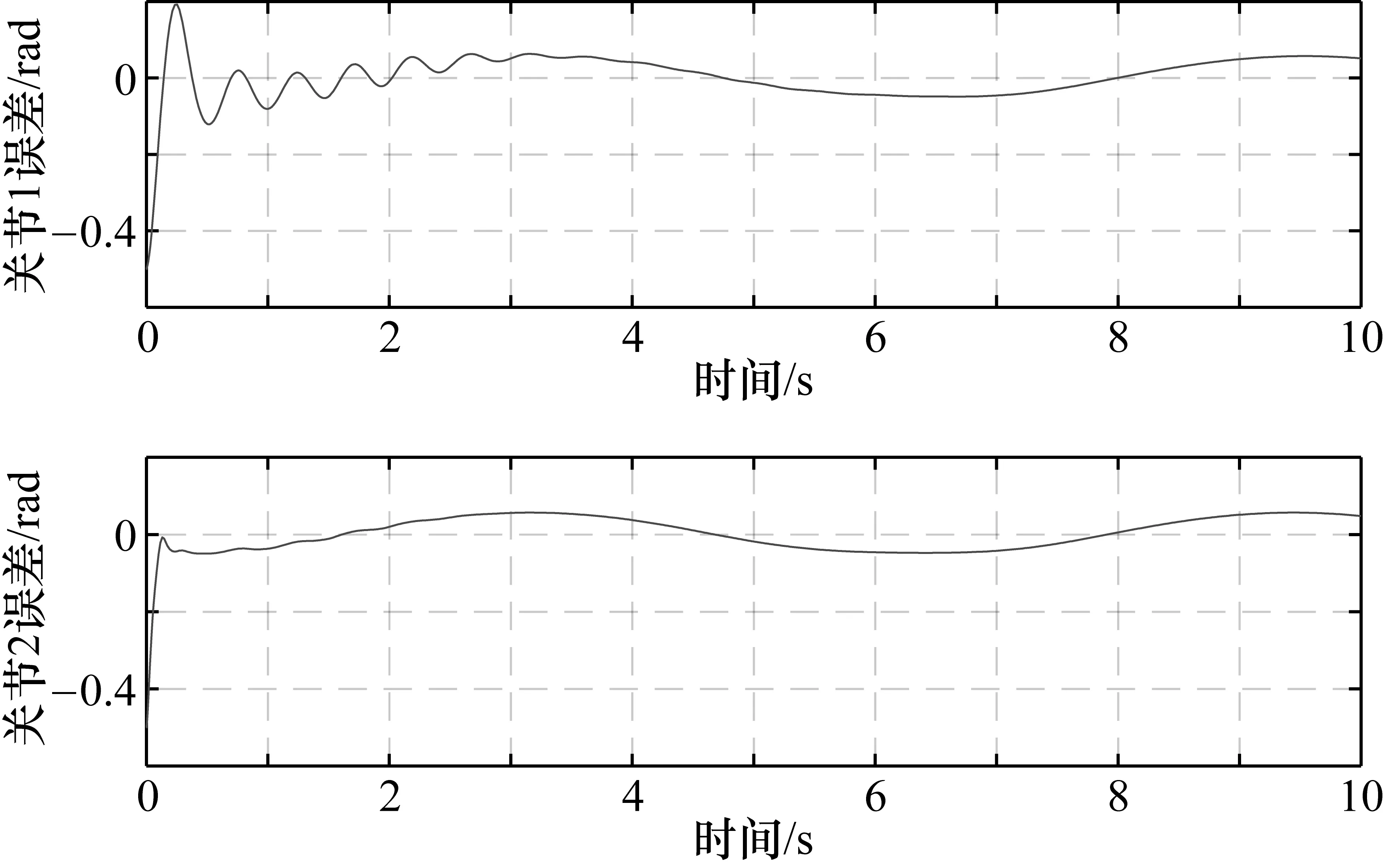
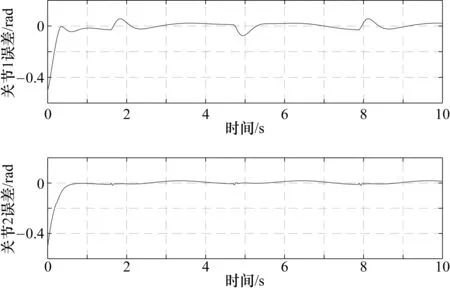
假設2 外部干擾信號d有界且界在機械臂系統可承受范圍,即|d| 由于指數趨近律具有參數可調節,趨近速度快,可在有限時間內收斂的優點,所以在此基礎上進行改進。 指數趨近律為 (2) 式中,k、ε均為常數;s為滑模面。 指數趨近律可以加快趨近滑模面的速度,但是由于其為帶狀,系統在向原點運動的過程中,不能趨近于原點,而是在原點兩側做抖振運動,會對機械臂造成損傷,對系統的跟蹤精度造成一定影響。因此,對指數趨近律進行了改進,如式(3)所示: (3) 由式(3)可以看出,式中加入了s2,在趨近運動的開始階段,由于離滑模面遠,運動速度快,系統誤差較大,但可以快速接近滑模面;隨著運動的進行,控制器的調節,系統誤差將逐漸變小,s2也隨之減小,系統逐漸趨于平穩,抖振有效減小。 由于式(3)中含有符號函數,符號函數實質上是分段函數,其切換具有不連續性,控制輸出一定會出現抖振現象;而飽和函數為連續函數,可使輸出平滑有界。因此,在改進控制律設計中采用雙曲正切函數來取代符號函數,雙曲正切函數為 (4) 其中,e為自然常數。 圖1為sgn(s)與tanh(s)的比較曲線,從圖中可以看出,tanh(s)連續且平滑,一次性穿越0點,這對趨近過程中的抖振現象有較好的抑制效果。 圖1 雙曲正切曲線與符號函數曲線比較 因此,改進后的趨近律為 (5) 由于 (6) 式(6)滿足趨近律到達條件,改進趨近律可以到達滑模面。在引入雙曲正弦函數抑制抖振的同時,系統的跟蹤速度會有所降低,為了保證系統的動態性能,在系統允許的范圍內,增大式(6)中的k值并相應減小ε可以使趨近過程變快,同時有效削弱系統抖振。 在機械臂控制系統中,給定一個輸入信號qd作為期望角度,輸入期望角度qd與實際角度q作差輸出誤差信號x,將該信號輸入到滑模控制器中,經過滑模控制器處理會輸出一個控制力矩T0與干擾觀測器經調整增益后輸出的力矩Td作差,產生最終的控制力矩T(即T=T0-Td),將T輸入機械臂系統中,從而實現對整個系統的控制。 由于存在外部干擾信號d,在控制器具體設計中將其分為兩部分:一部分為可觀測部分(如系統摩擦);另一部分為不可觀測部分(隨機外部干擾)。在具體設計中,可觀測的部分由干擾觀測器進行觀測,未觀測到的部分由滑模控制器進行補償,系統控制框圖如圖2所示。 圖2 基于干擾觀測器的機械臂滑模控制框圖 根據機械臂的數學模型,采用如下干擾觀測器: (7) (8) (9) 假設相對于干擾觀測器的動態特性,干擾的變化是緩慢的,即 (10) 由式(8)、式(10)可得干擾觀測器的動態方程為 (11) 將式(7)和式(8)代入式(11): (12) 綜合式(1)和式(7),可將式(12)變為 (13) 因而得到 (14) 干擾觀測器的輸出傳輸到增益調整模塊,將觀測到的干擾轉化成相應輸入通道的控制量,結合式(1)可知增益調整矩陣為單位陣,則 采取干擾觀測器后,可將式(1)的數學模型變為如式(15)所示: (15) 由式(15)可知,經干擾觀測器補償后,外界干擾由d減小為e,有效地減小了外界干擾對系統的影響。 假設機械臂期望關節角為qd,x=qd-q為誤差信號。設計滑模面為 (16) 當系統到達滑模面時,對于任意給定的初始點x(0),系統將穩定運行并在有限時間內到達平衡點。此外,通過設計常數矩陣B,可使控制系統具有較好的動態品質。 下面進行控制律的設計。由于誤差為x=qd-q,滑模面為 (17) 將滑模面求導,可得 (18) 將式(15)帶入式(18)中可得 (19) 由式(5)和式(19)可得控制律為 (20) 機械臂系統的動力學模型為[10]: 式中, p=[p1,p2,p3,p4,p5]=[0.29,0.076,0.087,0.304,0.087] 為了驗證所提控制策略的正確性和有效性,分別從軌跡跟蹤、位置跟蹤誤差以及干擾觀測結果3個方面比較傳統滑模控制策略與改進趨近律的控制策略。 圖3 傳統滑模控制軌跡跟蹤曲線(無干擾觀測器) 圖4 傳統滑模控制軌跡跟蹤曲線(含干擾觀測器) 比較圖3、圖4曲線可以看出,兩曲線在關節1處抖振明顯,跟蹤效果差;觀察關節2處的跟蹤曲線可以看出圖4中曲線的波動較小,可以大致跟蹤給定的軌跡,但其效果并沒有達到最優。說明干擾觀測器有效減小外界干擾對系統的影響,但系統仍然存在抖振現象。 圖5 改進趨近律的軌跡跟蹤曲線(含干擾觀測器) 對比圖4、圖5跟蹤曲線可以看出,采用改進趨近律的滑模控制策略,關節1處抖振明顯減小,關節2處在大約0.3 s時軌跡基本重合,說明改進趨近律可以有效減小抖振。 圖6 傳統滑模控制軌跡跟蹤誤差曲線(無干擾觀測器) 圖7 傳統滑模控制軌跡跟蹤誤差曲線(含干擾觀測器) 從圖6、圖7可以進一步看出,兩圖都有較大的跟蹤誤差,當采用干擾觀測器后,關節1在3 s以后誤差波動逐漸平穩,關節2的最大誤差減小到0.057 rad左右,說明干擾觀測器可以削弱外界干擾對系統的影響。 圖8 改進趨近律的軌跡跟蹤誤差曲線(含干擾觀測器) 比較圖7、圖8曲線,從圖7曲線可以看出未改進趨近律時跟蹤誤差較大,抖振幅度大,很難進行有效跟蹤;圖8曲線可以明顯看出采用改進控制律后,在0.6s以后,跟蹤誤差幾乎為0,跟蹤速度快且抖振小。 圖9為干擾觀測器觀測結果曲線,雖然在關節1轉折點處難以較好地跟蹤,但在關節2處可以實現對干擾的觀測。曲線表明采用干擾觀測器能夠快速準確地估計干擾信號,從而進一步對觀測到的干擾進行消除,減小干擾對系統的影響。 針對多關節機械臂滑模控制存在抖振與外界干擾的問題,設計了一種基于干擾觀測器的改進趨近律的滑模控制策略。在設計控制器的過程中,趨近律可以有效減小抖振,干擾觀測器對外界可觀測的干擾進行觀測,然后采用滑模控制器對其余的不確定部分進行補償,從而使系統輸出能跟蹤期望軌跡,保證系統的安全性和穩定性。仿真分析表明,與傳統滑模控制策略相比,該策略不僅能夠減小外界干擾對系統的影響,而且可以有效削弱抖振,加快系統響應速度,增強系統穩定性。2 趨近律設計
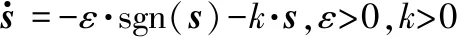

3 基于干擾觀測器的滑模控制器設計
3.1 干擾觀測器的設計
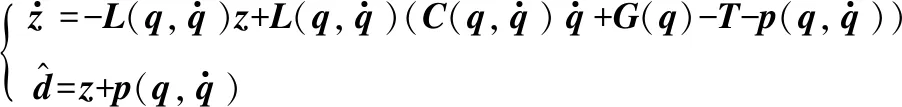
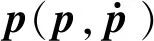
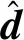

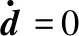
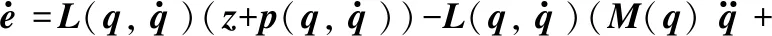
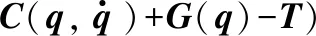

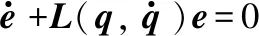
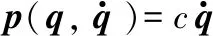
3.2 滑模面設計
4 仿真分析

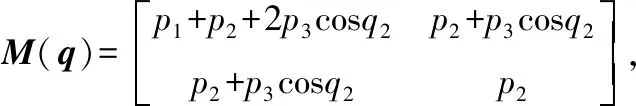



5 結束語

