基于VIP處理的O-PLS算法的無創血糖基礎研究

(上海工程技術大學 電子電氣工程學院，上海 201620)

血糖含量是診斷糖尿病的唯一標準，雖然通過醫療手段可以有效控制糖尿病[1]，但是目前全球尚無根治糖尿病的方法。為控制糖尿病，需要經常抽取靜脈血來測定血糖濃度，目前的監控方式主要有兩種：① 到醫院進行檢查；② 采用市場上的血糖檢測儀進行自我監控。為了使用方便，大多數患者都會選擇自我監控。但血糖檢測儀大都采用生化法對血糖的濃度進行測量，這種測量方法常伴有疼痛和患者傷口感染的風險，測量時血量的多少會直接影響到測量精度[2]，測量之后丟棄的試紙可能會造成環境污染。近年來，近紅外光譜技術的快速發展為血糖的無創檢測提供了技術支持，算法的快速發展讓糖尿病病人的高精度、無痛、實時的自我監控成為可能[3]。

本文結合光譜學原理，通過對不同濃度葡萄糖溶液的近紅外光譜的采集，PLS對光譜和濃度進行建模，利用OSC消除光譜和濃度主成分中的正交分量,增強光譜與濃度之間的相關關系，簡化模型，使得模型更加易于理解以及使用VIP篩選出對葡萄糖濃度解釋能力強的波長變量，提高模型的預測能力，使得PLS模型的準確度更高，預測的精準性得到明顯改善。

1 基本原理

1.1 偏最小二乘法

作為一種多元統計數據分析方法，PLS回歸模型將多元回歸模型問題降維，即將多元回歸問題分解為若干個一元線性回歸問題，適用于變量多而數據樣本少的建模問題。

使用葡萄糖溶液的光譜和其相應濃度建立的模型中，PLS的目標是使得葡萄糖溶液的光譜矩陣X的主成分向量t與其濃度矩陣y的協方差最大，即

(1)

式中,

(2)

由上述表達式可以看出，如果X的變量空間中包含與y正交的變化，則t和y的相關關系會很小。雖然t中包含了X的最大變化信息，但t與y的協方差不能最大化，這會導致模型的擬合性能較好而解釋性能變差。

1.2 正交信號校正法

為了解決由于葡萄糖溶液的光譜和濃度之間相關關系不大引起的模型的解釋性能較差的問題，在PLS回歸前使用OSC進行數據的預處理[5]。如果光譜中包含與濃度無關的系統變化信息，即光譜中包含與濃度正交的信息時，則必定會反映在光譜和濃度的主成分矩陣中[6]。OSC去除了光譜主成分矩陣t中所包含的與濃度矩陣無關的部分，用校正后的信號進行PLS回歸，提高了光譜主成分矩陣中含有的濃度信息，增強了模型的解釋能力[7]。

O-PLS(Orthogonal Signal Correction-Partial Least Squares)方法處理步驟如下。

首先將原始的葡萄糖溶液的光譜數據和濃度數據進行規范化(中心化和方差歸一化)處理，得到光譜矩陣X和濃度矩陣y。

① 計算X的權值向量：取u=y，計算wT=uTX/(uTu)。

② 將w歸一化：w=w/‖w‖。

③ 計算主成分向量t，t=Xw。

④ 計算負荷向量p，p=XTt/(tTt)。

⑤ 計算p和w正交的分量p0=p-[w(wTw)-1wTp]。由pTw=1知p在w上的投影與w相等，取w0=p0=p-[w(wTw)-1wTp]，w0為w的正交分量。

⑥ 將得到的w0歸一化：w0=w0/‖w0‖。

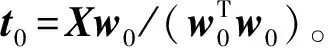
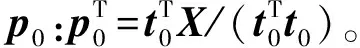
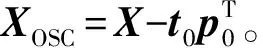
⑩ 若仍需要去除正交成分，則用XOSC代替X，重復上述步驟③～步驟⑨。

OSC每一步中都去除光譜矩陣X中與濃度矩陣y無關的成分，所以即使原來的光譜矩陣X和濃度矩陣y的相關性不大，去除足夠多的正交成分后，光譜矩陣X的剩余部分和濃度y的相關性將變大，大大簡化了原始的PLS模型，使得模型更加易于解釋和理解。

1.3 變量投影重要性指標

PLS方法中，通常通過變量投影重要性指標來表征光譜中波長變量和濃度的相關關系。具體計算公式如下：

(3)

式中，q為原波長變量的個數；wj是w的第j個分量，為第j個波長變量的權值。

從模型預測的角度來說，如果某一波長在解釋濃度時起的作用很小，則可以考慮刪去這個波長變量后重新建模。基于VIP對波長進行篩選后再采用PLS建模。

2 實驗及數據分析

2.1 實驗儀器

本實驗使用純葡萄糖和蒸餾水來配置濃度為1.8%～18%的葡萄糖溶液，采用Thermo Scientific AntarisTMntarisSci過程分析儀來收集葡萄糖溶液的光譜信息，光譜波長范圍為12000～4000 cm-1(833～2500 nm)，精度為±0.1 cm-1(0.02 nm at 1250 nm)。光譜掃描32次取平均以消除隨機誤差的影響。

2.2 數據分析

2.2.1 PLS對葡萄糖濃度和全光譜建模

在進行葡萄糖溶液的全光譜檢測時，選取溶液濃度區間為1.8%～18%,間隔1.8%，每個濃度配置3個樣本，控制測量條件不變的情況下每個樣本檢測3次，即每個濃度值有9個光譜數據樣本。每個濃度取6個葡萄糖溶液的光譜樣本作為訓練集，3個葡萄糖溶液的光譜樣本作為測試集，對葡萄糖光譜和濃度進行因子分析，得出主成分圖如圖1所示。

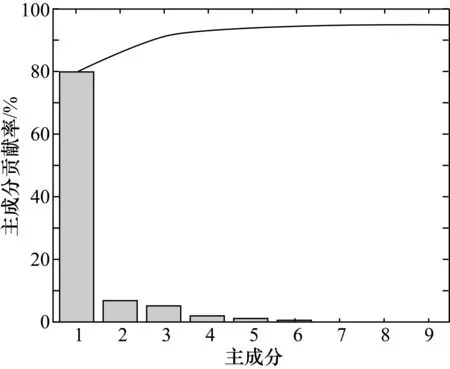
圖1 主成分貢獻率圖

圖1中，橫坐標為第i個主成分，縱坐標為主成分的貢獻率。由圖1可以看出，第一個主成分的貢獻率達到了80%左右，即系統信息的可解釋變異達到了總變異的80%左右，此時可認為回歸方程的精度已經達到要求。所以本文選取一個主成分進行建模后得到R2和RMSEP的值如表1所示(其中，每個葡萄糖濃度的光譜樣本用數字1～9來表示)。

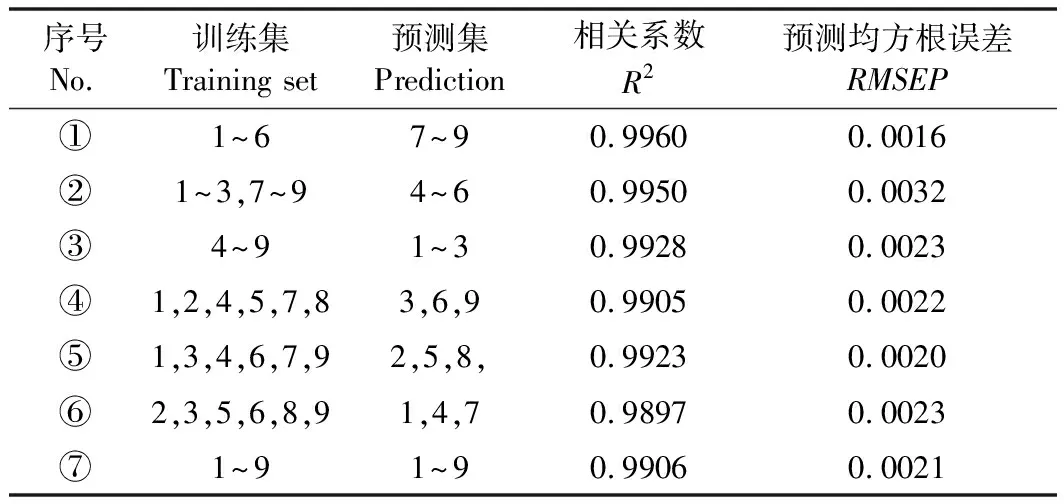
表1 PLS模型的R2和RMSEP

由表1可得，通過PLS建模所得到的模型驗證集的真實值和預測值的相關系數R2均在98%以上，RMSEP的值在0.0022左右，模型的預測效果較好，精度較高，具有較強的泛化能力。為了驗證OSC和VIP確實可以提高模型的精度和預測能力，本文選用R2較小，RMSEP值較大的No.6組樣本數據來進行處理建模。

2.2.2 OSC對樣本全光譜數據的處理

一元回歸分析中，經常采用散點圖來直觀地分析自變量和因變量之間的相關關系[9]。在PLS中，使用光譜和濃度的主成分t1和u1平面圖來反映光譜和濃度的相關關系，如圖2所示。

圖2為直接使用PLS建模的葡萄糖溶液觀測樣本的第一主成分偶對(t1,u1)散點圖，雖然t1和u1的關系近似于一條直線，符合光譜矩陣和濃度矩陣之間的線性關系，但是從圖上可以明顯地看出有些點偏離直線較遠，即這些點的光譜矩陣X和濃度矩陣y之間的正交成分過多，相關性不大。

圖2 葡萄糖溶液觀測樣本的t1/u1散點圖

為了解決上述問題，先使用OSC對數據進行預處理再使用PLS建模。得到的處理結果如圖3所示。

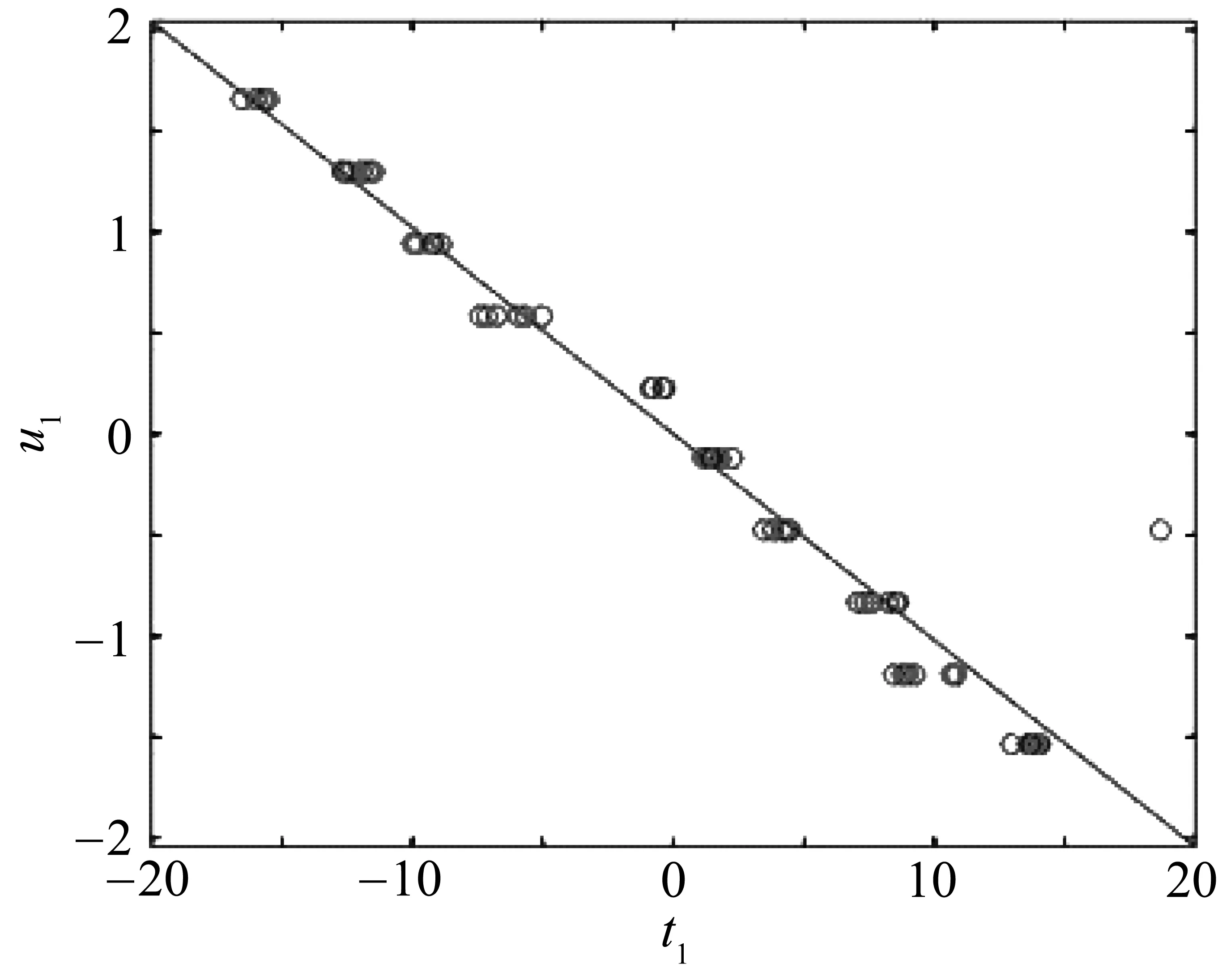
圖3 經過OSC處理后的葡萄糖溶液觀測樣本的t1/u1散點圖

由圖3可以看出，經過OSC處理后的第一主成分偶對(t1/u1)更加接近于一條直線。OSC處理后，對光譜和濃度使用PLS進行建模，模型由原先的R2=98.97%，RMSEP=0.0023變成R2=99.68%和RMSEP=0.0013，此時認為采用OSC方法有效地剔除了光譜矩陣和濃度矩陣之間的正交部分，增強了光譜和濃度之間的相關關系，使得模型的精度和預測精度得到了有效的提高。

2.2.3 經過OSC處理后再使用VIP對樣本全光譜數據的處理

對于經過OSC處理后的全光譜數據采用VIP來觀察光譜對葡萄糖溶液濃度的解釋作用，觀察結果如圖4所示。

圖4中，橫坐標為波長變量個數，縱坐標為相應波長變量的變量投影重要性指標。通過圖4可以看出，波長變量個數在500～600區間段內的VIP值較大，即波長變量對葡萄糖溶液濃度的解釋作用較大，這一區間段對應的葡萄糖的波長范圍為1596～1732 nm，正處于葡萄糖溶液在近紅外檢測的特征波段內。通過分析變量投影重要性指標挑選出90個對葡萄糖溶液建模解釋作用最大的波長變量，通過對這90個光譜波長變量進行建模，模型的R2達到了99.73%，RMSEP為0.0052。

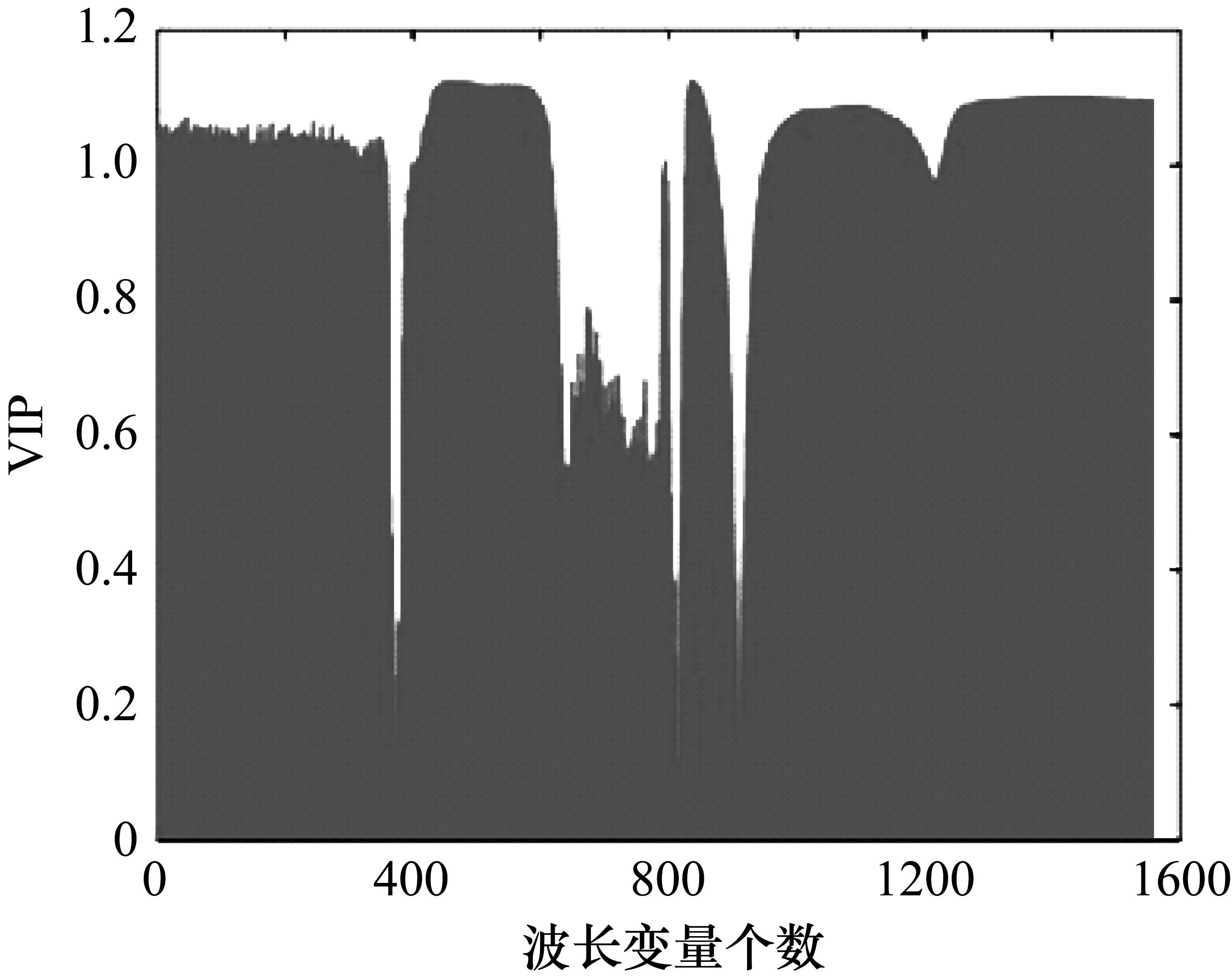
圖4 全波長變量對葡萄糖溶液的變量投影重要性

由于人為因素以及儀器的測量誤差，實驗所采集的樣本中存在異常樣本點，通過對OSC和VIP處理后的測試集數據樣本做主成分分析得到得分圖如圖5所示，其中黑色點22，59，60代表異常樣本，灰色的點為正常樣本。

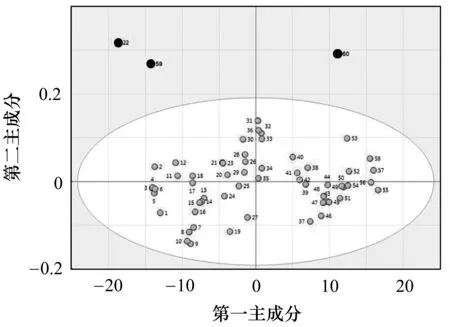
圖5 數據經過OSC和VIP處理后的得分圖

剔除3個異常樣本后，再次進行PLS建模，模型驗證集的真實值和預測值的相關系數R2達到了99.77%，RMSEP為0.0048，模型的解釋能力和精度都得到了提高。最終的模型預測結果如圖6所示。

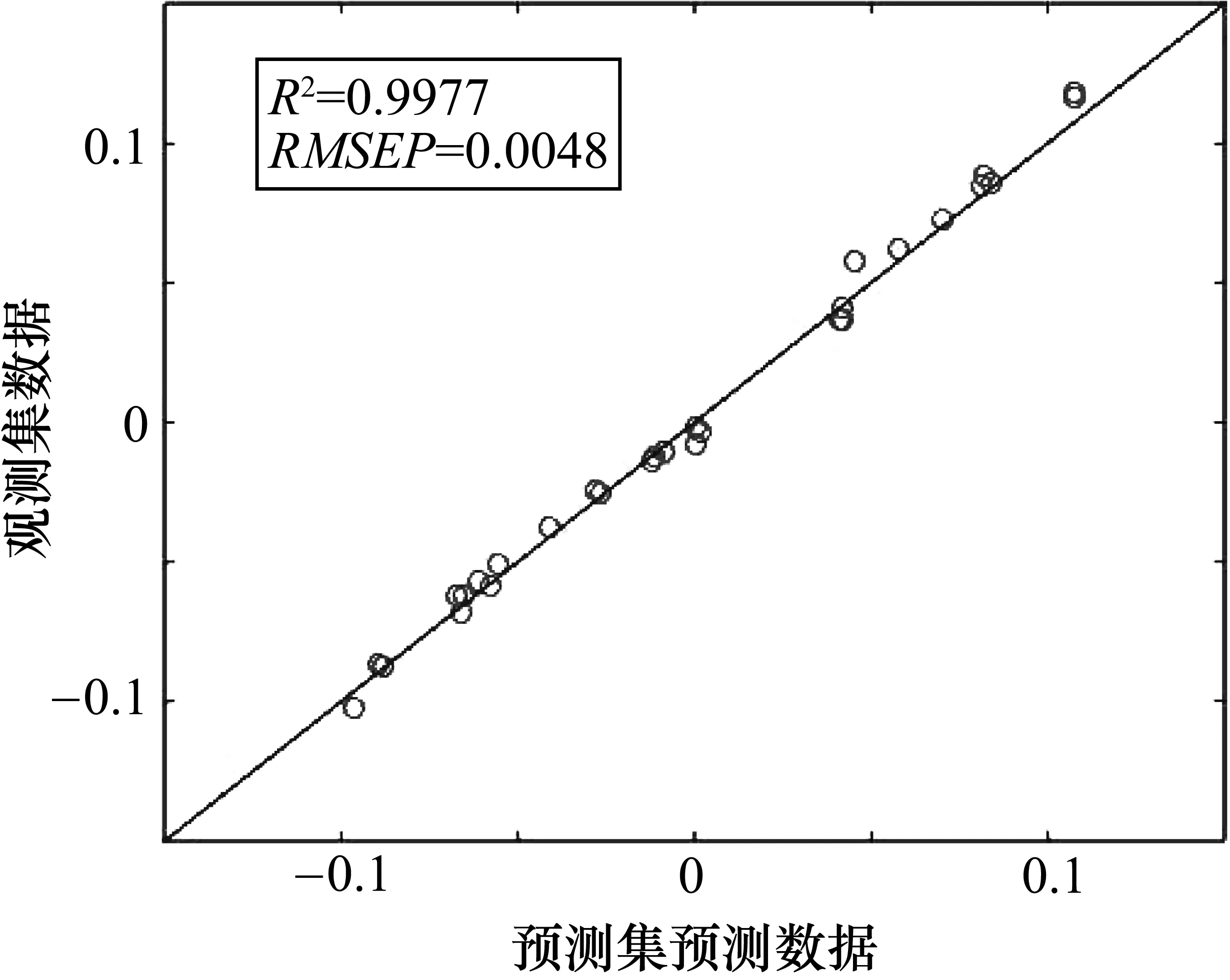
圖6 模型最終預測結果

圖6中，數據擬合的效果接近于一條直線，即預測集通過VIP處理的O-PLS算法處理后，模型的預測結果幾乎近似于實際測得的值，模型的預測精度較高。

通過式(4)計算采用VIP和OSC處理后的數據進行PLS處理與直接使用PLS處理的相關系數的相對提高值。

(4)

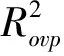
3 結束語

通過VIP處理的O-PLS算法對葡萄糖溶液的光譜和濃度數據進行建模，結果表明，通過OSC可以有效地剔除光譜和濃度的主成分中的正交成分，增強光譜和濃度之間的相關性。采用變量投影重要性指標(VIP)來分析PLS回歸方程中波長變量對葡萄糖溶液濃度建模的解釋能力，去除不相關的波長變量，有效地提高了整個模型的預測精度。相比不做數據處理的PLS，模型驗證集的真實值和預測值的相關系數相對提高了77.67%。