基于PCA優化的神經網絡飛機燃油消耗預測方法

(空軍工程大學 航空工程學院，陜西 西安 710038)

飛機是一種燃油消耗巨大的航空器。對于民用飛機而言，航空燃油消耗直接關系到航空公司的運營效益[1]；對于軍用飛機而言，燃油消耗對地面保障和任務規劃影響極大。對飛機的燃油消耗進行合理預測，并以此為基礎對燃油進行管理、規劃飛行任務等對于提升航空運輸的經濟性與飛機的任務能力都具有重要意義。

飛機燃油的消耗受到諸多因素的影響，而且多個影響因素之間存在極強的非線性耦合效應，導致利用傳統方法對飛機燃油消耗建模存在較大困難。文獻[2]和文獻[3]分別利用多元線性回歸模型和基于隨機森林算法建立的回歸模型對飛機燃油消耗進行了預測，模型較為簡單，但忽略了飛發交互效應和非線性因果關系；文獻[4]和文獻[5]建立了基于能量守恒原理的燃油消耗模型，主要缺點是模型性能參數難以獲得，且沒有考慮氣象條件以及飛機“油耗油”問題對油耗的影響[6]；文獻[7]提出了基于軌跡模式識別的計算方法，主要用于估算，不宜精確預測；文獻[8]利用飛行動力學方程建立了飛機燃油消耗動力學模型，預測精度還有待提高。Chang等人建立了基于飛行數據模糊邏輯模型的運輸機燃油消耗模型[9]，預測的精度較高，但模型較為復雜；Park等人利用飛行軌跡數據和總能量模型飛燃油消耗進行了估算[10]，解決了工程實際應用困難的問題，但在精度上有所欠缺；Vazquez等人利用動力學數值分析建立了飛機的油耗模型[11]，具備可操作性強的優點，但是其諸多理想化假設條件忽略了發動機工況等對燃油消耗的影響因素。Khadilkar[12]等利用飛參數據建立了燃油消耗多變量函數模型，變量數據在工程實際中難以獲得；飛參數據是記錄的飛機、發動機以及其他設備的狀態數據，是建立飛機燃油消耗的重要依據[13]。Elman神經網絡適用于預測時間序列，對于受歷史飛行狀態影響較大的耗油速率適應性較好。鑒于以上分析，本文選取了Elman神經網絡，經過主成分分析法降低輸入維數，利用Elman神經網絡對飛機燃油消耗進行了預測，并將該網絡與其他網絡及未經PCA法處理的Elman網絡進行了對比，最后利用K-S檢驗法驗證了其預測誤差服從正態分布，并依據驗證結果對預測值進行了進一步修正。

1 主成分分析基本原理

主成分分析法(Principal Component Analysis，PCA)是一種降維處理方法，通過線性變換轉變為其他幾個不相關的指標，新指標按照方差遞減順序依次排列[14]。

1.1 歸一化處理

設有n個相互關聯的m維變量作為輸入，記為X1,X2,…,Xn，樣本采集數為j,則樣本矩陣Xm×n為

(1)

其中,

(2)

(3)

(4)

令

(5)

即完成原始樣本矩陣的歸一化處理。

1.2 計算各變量之間的相關矩陣R

(6)

其中,

(7)

l=1,2,…,m;p=1,2,…,m;q=1,2,…,n。

1.3 計算主成分

利用Jacobian法求解相關矩陣R的所有特征值λk(k=1，2，…,n)及其對應的特征向量并將特征根由大到小排列，分別計算出對應的主成分。主成分計算需要確定主成分的個數，一般由方差貢獻率和累計貢獻率確定。

主成分Zk的方差貢獻率Pk為

(8)

式中,λk為主成分Zk在全部方差中所占的比重。前c個主成分的累計貢獻率Pc為

(9)

2 實例建模分析

2.1 飛機燃油消耗因素的主成分分析

輸入的飛參數據數據項經過篩選后一共有21項。現對經過歸一化處理后的數據進行主成分分析，經過主成分變換后，原先的21個變量經過線性變換為21個主成分，按照大于80%的累計貢獻率進行篩選，最終只留下前5個主成分作為神經網絡輸入。現給出前5個主成分按照特征值、方差貢獻率以及累計貢獻率，如表1所示。

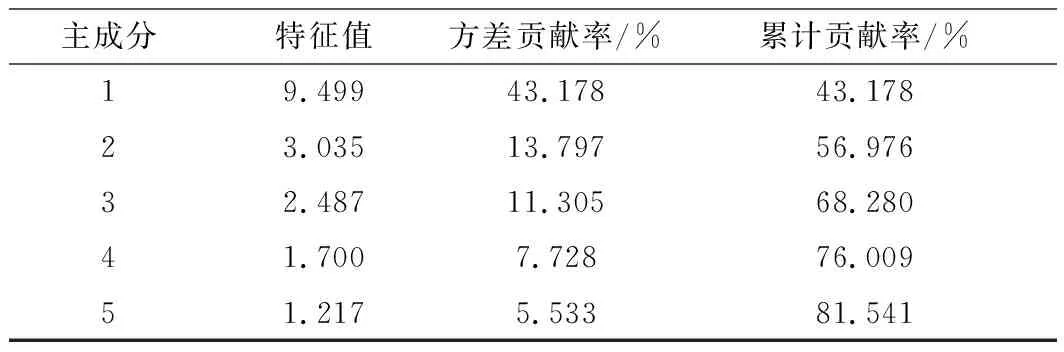
表1 主成分的特征值、方差貢獻率與累計貢獻率

成分矩陣反映了主成分包含的原有變量信息的豐富程度。數值越大，則表明該主成分包含的某原始變量的信息越多。主成分與原始變量的關系可以得到這5個主成分的反映原始數據信息的能力，如表2所示。第1主成分主要包含了發動機因素(發動機的各項狀態參數，縱向加速度很大程度上取決于發動機推力)、大氣因素(飛行高度)、速度因素(馬赫數)、重量因素(總剩油量)；第2主成分主要包含了爬升因素(俯仰角、升降速度)；第3主成分主要包含了速度因素(飛行速度、馬赫數，發動機進口氣流總溫取決于來流速度)；第4主成分主要包含了升力因素(法向加速度、迎角)；第5主成分主要包含了機動因素(橫滾角，側向加速度)。

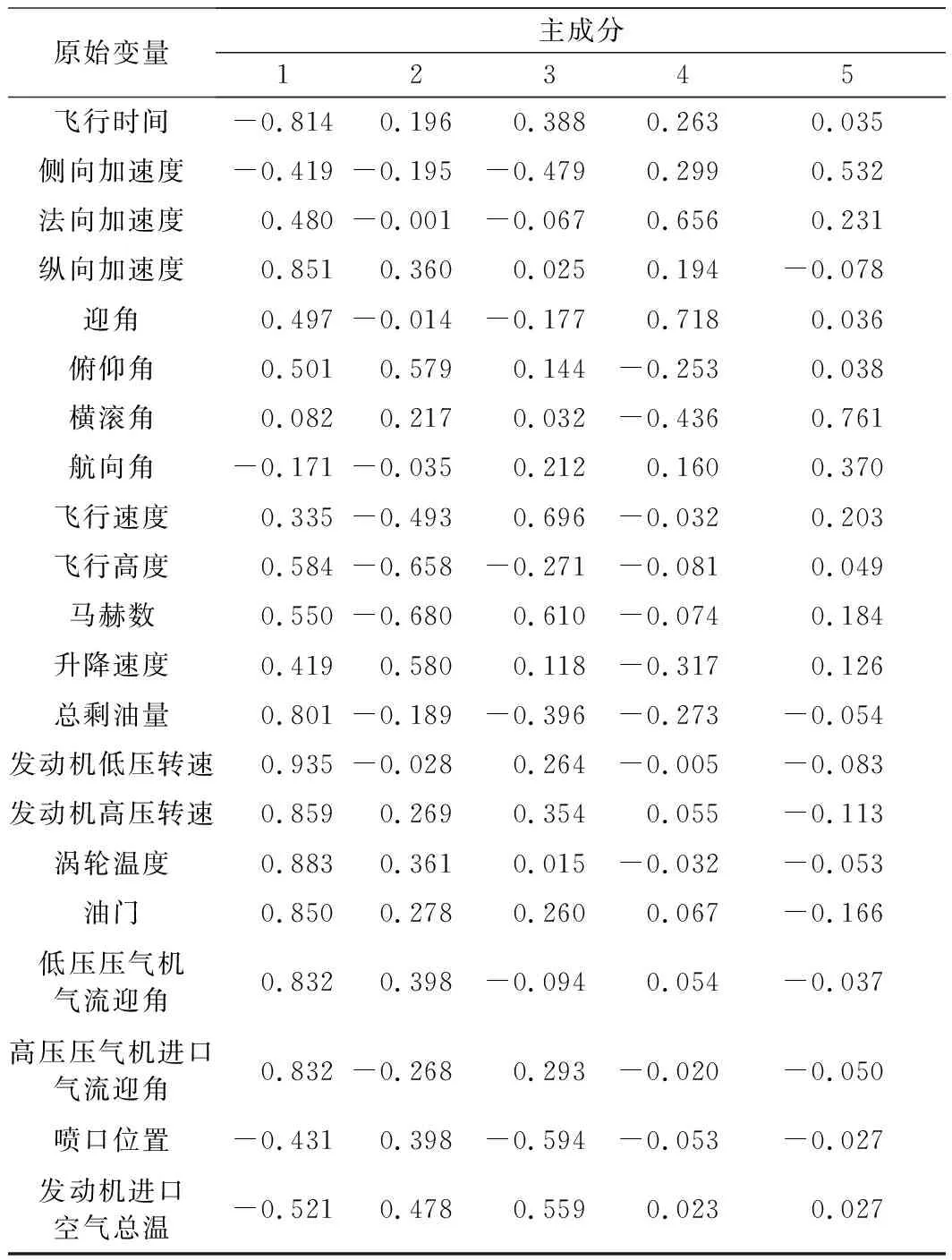
表2 成分矩陣所含信息

可見這5個主成分能夠充分反映21個原始變量的有效信息，對所有的影響因素進行了解耦和線性組合，并與實際影響飛機燃油消耗的因素相符合，在充分保留原有信息的同時進行了降維處理。

2.2 飛機燃油消耗的神經網絡預測

2.2.1 訓練數據和測試數據的選取

為了充分證明Elman神經網絡對飛機燃油消耗預測的準確性，本文對某型同架飛機不同飛行剖面的兩個架次飛參數據進行了采集，并將一個73 min的飛行架次采集的飛參數據作為訓練數據，將另一個47 min的飛行架次的數據作為測試數據進行預測，兩個架次分別稱為架次1和架次2，采集時間間隔設定為1 min，以避免樣本數過多產生過擬合。

2.2.2 神經網絡結構設計

經過試驗，網絡一共包含30個神經元，其中隱含層包含10個神經元，輸入和輸出層均包含10個神經元。訓練函數為traingdx函數，輸入層到隱含層的傳遞函數為transig函數，隱含層到輸出層的函數為purelin函數。

2.2.3 訓練和測試

經過10000次迭代后，網絡的均方誤差(MSE)已經降低到10-3以下，符合飛機燃油消耗預測的需求。利用訓練完畢的網絡進行預測，平均相對誤差為4.29%，均方相對誤差為0.34%，符合工程上的誤差要求。為訓練和預測的結果對比，如圖1所示，利用架次1數據訓練得到的網絡仍然能對架次2有良好的預測效果，說明主成分分析與Elman神經網絡結合的方法能夠充分挖掘飛參內部的有效信息，具備良好的非線性映射能力。

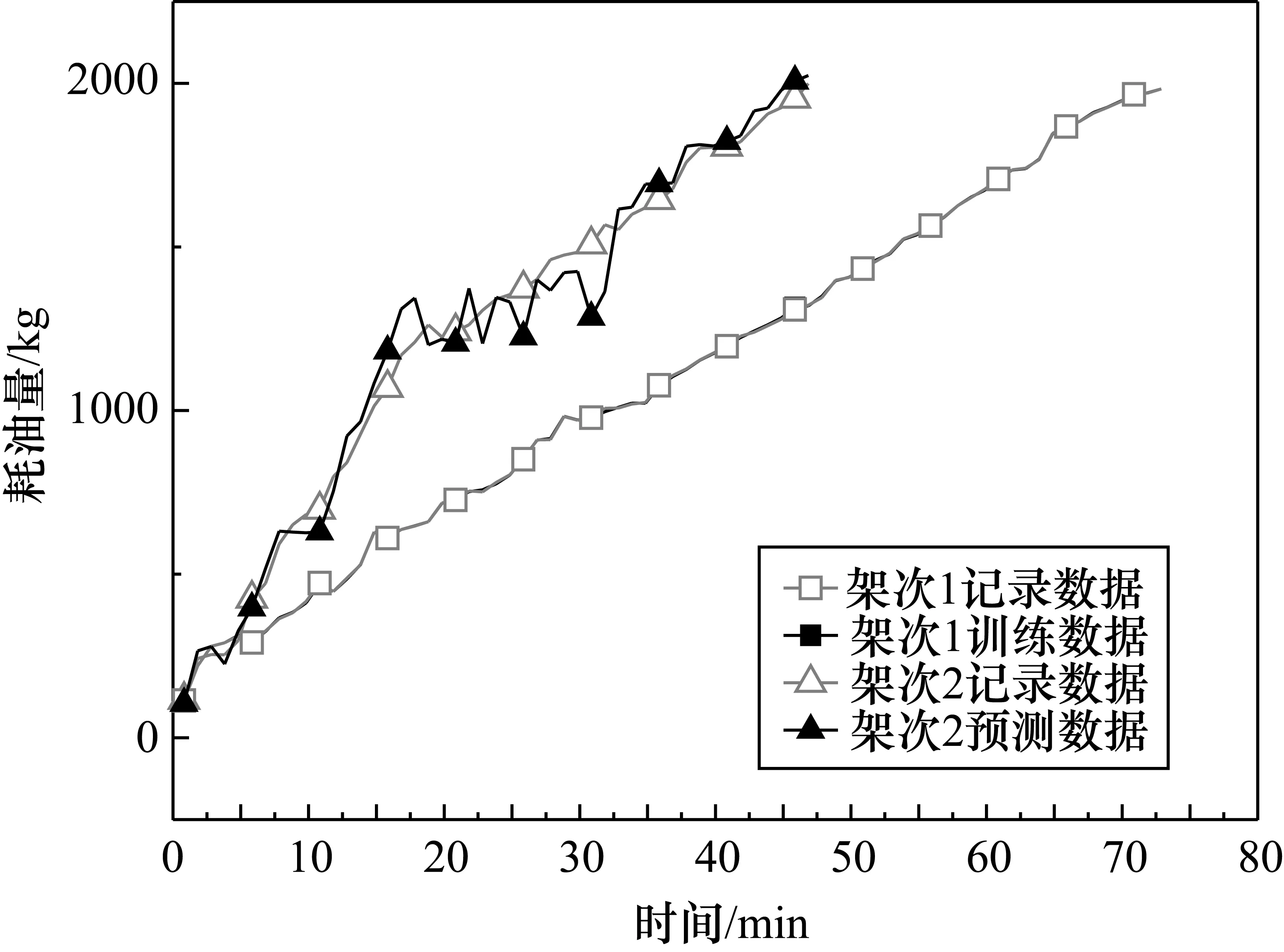
圖1 Elman神經網絡訓練和預測結果

現利用在主成分分析基礎上的BP、GRNN和RBF 三種神經網絡,未經過主成分分析法處理的Elman神經網絡的預測結果以及經過主成分分析法處理的Elman神經網絡進行對比。5種預測方法的預測結果與飛參系統記錄數據的對比如圖2所示。可以看出，BP網絡的預測趨勢雖然基本符合油耗規律，但是部分區間預測結果波動過大，且出現大量尖峰值；GRNN網絡只能大體給出油耗趨勢，預測值則與實測值之間的差值過大；RBF網絡則出現病態數據。

未經主成分分析法降維處理的網絡的預測效果不如經過主成分分析法優化的Elman網絡，但是卻仍然遠優于其他三種網絡;經主成分分析法處理后的Elman神經網絡擬合效果更接近真實值，3項誤差指標分別只有未經處理的6.45%、29.96%、22.24%，在網絡的訓練時間上提升了6 s,如圖3與表3所示。由此可以得出結論，Elman神經網絡的經過主成分分析降維處理后的網絡在誤差性能和收斂性上均有較大提升。

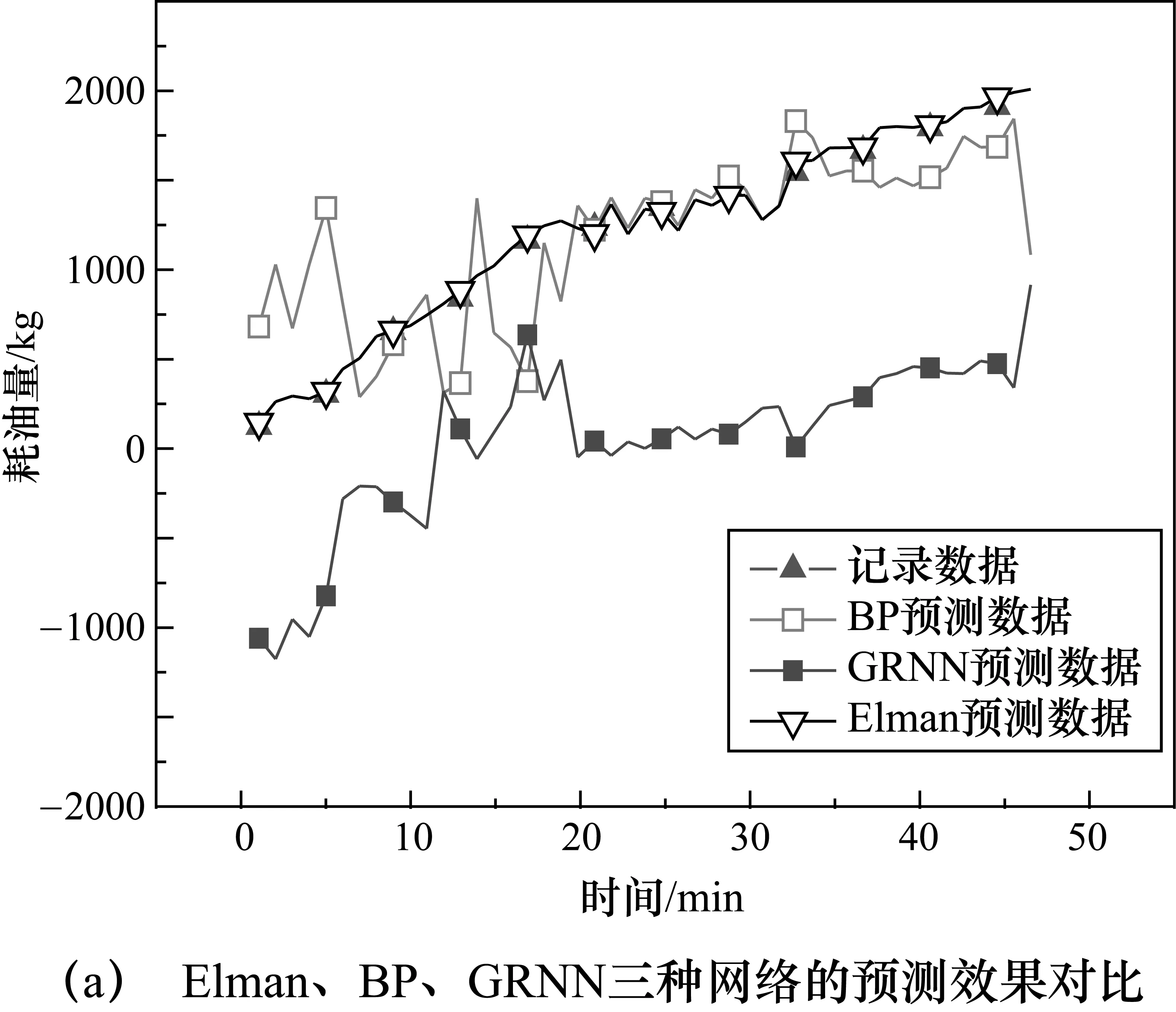
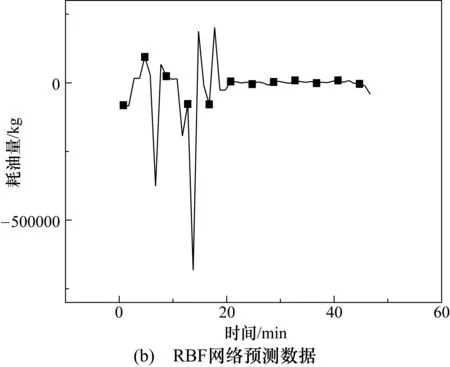
圖2 不同網絡預測效果對比

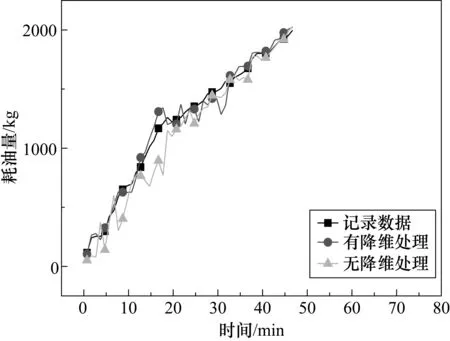
圖3 有無主成分降維處理預測效果對比

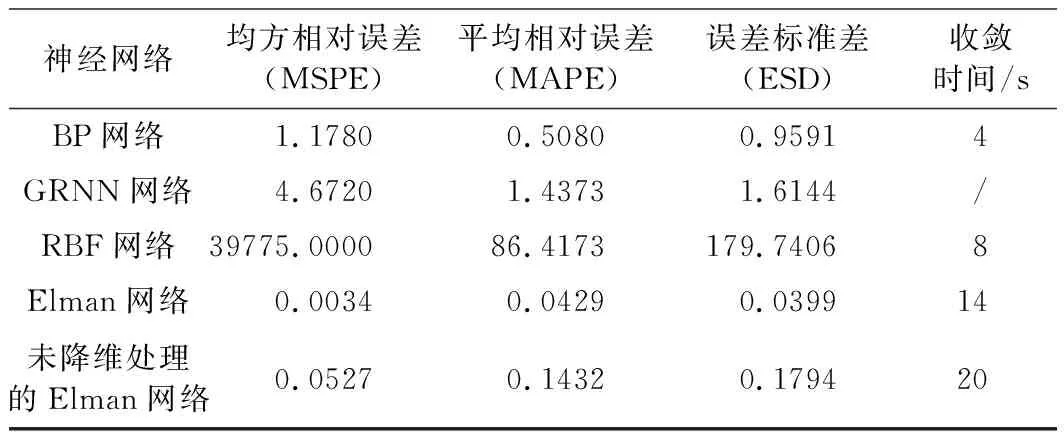
神經網絡均方相對誤差(MSPE)平均相對誤差(MAPE)誤差標準差(ESD)收斂時間/sBP網絡1.17800.50800.95914GRNN網絡4.67201.43731.6144/RBF網絡39775.000086.4173179.74068Elman網絡0.00340.04290.039914未降維處理的Elman網絡0.05270.14320.179420

3 基于K-S檢驗法的預測結果冗余修正

在工程實際問題中，往往需要設計有一定的冗余度或設置安全系數。為滿足飛行安全要求，現對誤差分布進行研究并求得安全系數β，修正預測結果。現提出一種基于Kolmogorov-Smirnov檢驗法(以下簡稱“K-S檢驗法”)的預測結果冗余修正方法。令實際值為U=[U1,U2,…,Ut]T,預測值為V=[V1,V2,…,Vt]T，實際值與與預測值之間的相對誤差為δ=[δ1,δ2,…,δt]T(此例中t=47)，顯著性水平α=0.05，對誤差進行K-S檢驗是否服從正態分布。K-S檢驗的漸進顯著性為0.827，大于顯著性水平α，接受原假設，并服從N(-0.003,0.0049)分布，結果如表4所示。

表4 誤差分布的K-S檢驗結果

取燃油預測值置信度為95%的置信區間[a,b]=[-0.0232,0.0170]，取置信區間下限的相反數為預測結果安全系數β=-a=0.0232,則經修正后的預測值為VM=(1+β)V,即經過修正后的燃油消耗的預測值是原始預測值的102.3%，保證飛機預測油耗在95%的可能性下高于實際油耗。

4 結束語

(1) 利用主成分分析法將21個飛參參數簡化為5個主成分，分析了成分矩陣，降低了神經網絡的輸入維數，提高了Elman神經網絡的性能。將主成分分析得到的數據作為輸入，對某架次的飛機燃油消耗進行了預測，結果表明預測值與實測數據偏差較小。

(2) 將Elman神經網絡的預測結果與其他幾種網絡以及未經主成分分析法改進的神經網絡進行了對比試驗，驗證了前期網絡篩選的結果，也證明了主成分分析法對神經網絡性能具備改進作用。

(3) K-S檢驗法證明Elman網絡的預測誤差服從正態分布，以此為基礎，為保證飛行安全冗余，利用95%置信區間下限得到安全系數β,進而得到修正后的預測值。

(4) 針對飛行燃油消耗的神經網絡的結構優化可以做進一步研究，以提高預測性能。