基于剪式控制力矩陀螺的低軌衛星垂軌擺掃姿態控制*
曹永奎 廖育榮 倪淑燕 楊新巖
1.航天工程大學研究生院,北京101416 2.航天工程大學職業教育中心,北京 101416 3.航天工程大學電子與光學工程系,北京 101416
針對大范圍區域進行持續性監測,對于環境管理、空天安全等都具有重要意義。借助衛星姿態機動來調整探測器主軸方向,通過視場拼接實現大范圍探測是低軌衛星實現大面積對地觀測的有效手段[1-2]。當前衛星多采用多條帶成像[3]方式來滿足大范圍探測的需要,在這樣的方式下,衛星一次過頂的時間內,部分時間必須用于衛星姿態調整[4],縮減了實際探測時間[5];部分研究通過掃描軌跡規劃提高過頂時間利用效率[6-7],但仍需要在成像間隙調整姿態。沿垂軌方向的掃描成像方式,能在整個過頂過程中都進行探測,但目前僅有線陣掃描方式[8],未見星載面陣相機的垂軌擺掃應用。
垂軌擺掃方式對衛星姿態機動能力提出很高的要求。現常用的姿態執行機構有噴嘴、反作用飛輪、磁力矩器,控制力矩陀螺等。控制力矩陀螺(Control Moment Gyroscope,CMG)具有精度高、力矩大的特點[9],是低軌成像衛星的首要選擇。在使用CMGs時,當前一般采用金字塔型、四棱錐和五棱錐型安裝,這類方式一般只能對稱安裝,且存在內部奇異,需要用特殊方式避免或逃離奇異位置[10-12]。任務要求衛星按照預定軌跡快速姿態機動,需要執行機構提供大力矩輸出。剪式CMGs在輸出上具有操縱律簡單、力矩解耦合[13-15]的特點,本文使用剪式CMGs作為執行機構。
針對衛星姿態垂軌擺掃,使用三軸非對稱安裝的剪式CMGs作為執行機構設計姿態控制系統,簡化陀螺框架角操縱律,避免系統出現內部奇異,減小了執行機構質量,實現衛星姿態的快速擺動。
1 垂軌擺掃大范圍探測過程
如圖1所示,利用低軌成像衛星對于目標區域進行大范圍掃描探測,需要利用成像衛星的姿態控制能力,調整衛星成像載荷對地指向,實現比傳統低軌探測方式更大的檢測范圍。
圖1 使用垂軌擺掃進行大范圍探測
衛星到達目標區域上空,從區域的一端開始探測,完成后調整視場垂直軌道移動,進行下一次探測,使2次探測視場之間能夠拼接成一個更大的視場,如此反復直到探測視場移至目標區域另一端,形成一個垂直軌道的帶狀區域;之后又反向重復此過程。如此反復直至覆蓋整個區域,在此過程需要衛星進行精準的三軸姿態機動。
實際擺掃中為簡化姿態控制,可以只進行滾動角調整進行垂軌擺掃,沿軌方向可由衛星的軌道運動進行推進。
如圖2所示,探測中2個視場之間有重復區域,這能保證拼接效果以及實現多次探測,提高對于微小目標或弱強度目標的監測概率。需要注意的是,實際運動中由于垂軌運動為變速,因此指向軌跡不是簡單折線,而是曲線,但只要前后2個周期的探測視場在沿軌方向剛好實現拼接,對于圖像拼接就沒有影響。
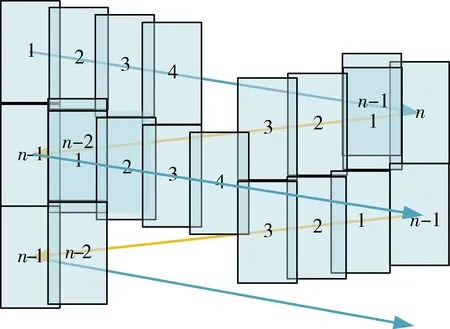
圖2 垂軌擺掃探測的視場拼接
本文設定相關任務參數如下:
h=500km,R=6400km
s=a×b=100×100km2
S=l×w=1000×1000km2
其中,h為軌道高度;R為地球半徑;s為探測器單幅探測面積;a為沿軌幅寬;b為垂軌幅寬;S為探測目標區域面積;為l表示區域沿軌長度;w表示區域垂軌寬度。
在此設定下,任務總時間為:
(1)
式中,GE=3.986×1014m3/s2為地球引力常數, 探測推進長度為akm時,(擺掃一個來回)時間為:
(2)
在一次任務中,需要進行10次垂軌擺掃來完成對整個目標區域的探測,并且重復區域的大小不會影響擺掃周期,可以通過控制探測器探測幀率來控制重復率,即重復率不會改變對于衛星姿態控制的需求。
2 垂軌擺掃軌跡設計
綜合考慮衛星成本以及性能要求,衛星擺掃時的姿態變化應按照特定軌跡進行,從而保證視場拼接。本文所述擺掃運動,繞著星體的橫滾角轉動,因此進行軌跡設計的時候,主要考慮衛星橫滾角的機動,默認衛星的另外2個姿態角保持不變(僅在空間干擾力矩作用下存在微小變化)。
2.1 恒角加速度姿態運動
恒角加速度運動即是保持角加速度值為恒定的運動,是較簡單的轉動形式。在衛星執行機構的最大力矩確定時,恒角加速度運動是一種時間最優的姿態機動軌跡。在一個擺掃周期內,其各個運動學參量的關系如下:
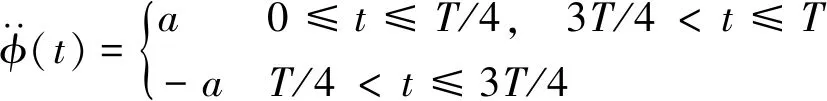
(3)
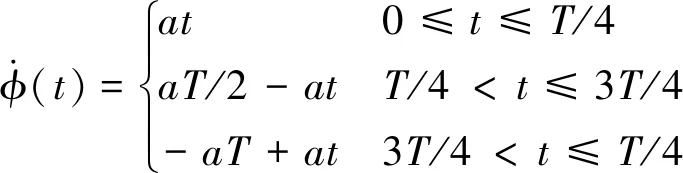
(4)
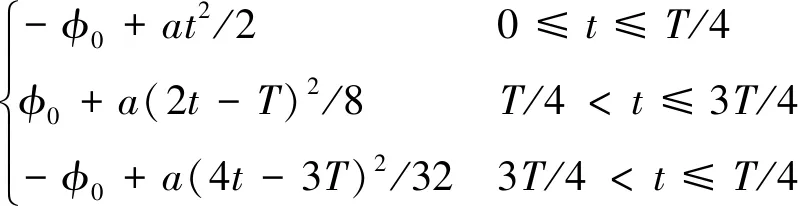
(5)
進行這樣的恒角加速度的姿態機動時,角加速度存在突變,對于執行機構要求高,并且會導致衛星的撓性振動。
2.2 正弦角加速度姿態運動
如圖3所示,正弦加速度運動的加速度曲線滿足正弦關系。正弦加速度軌跡平滑,對于星體和控制器件之間沒有力和力矩的突變,有利于衛星的穩定運行,尤其對于撓性衛星,正弦加速度運動能夠有效避免衛星振動。
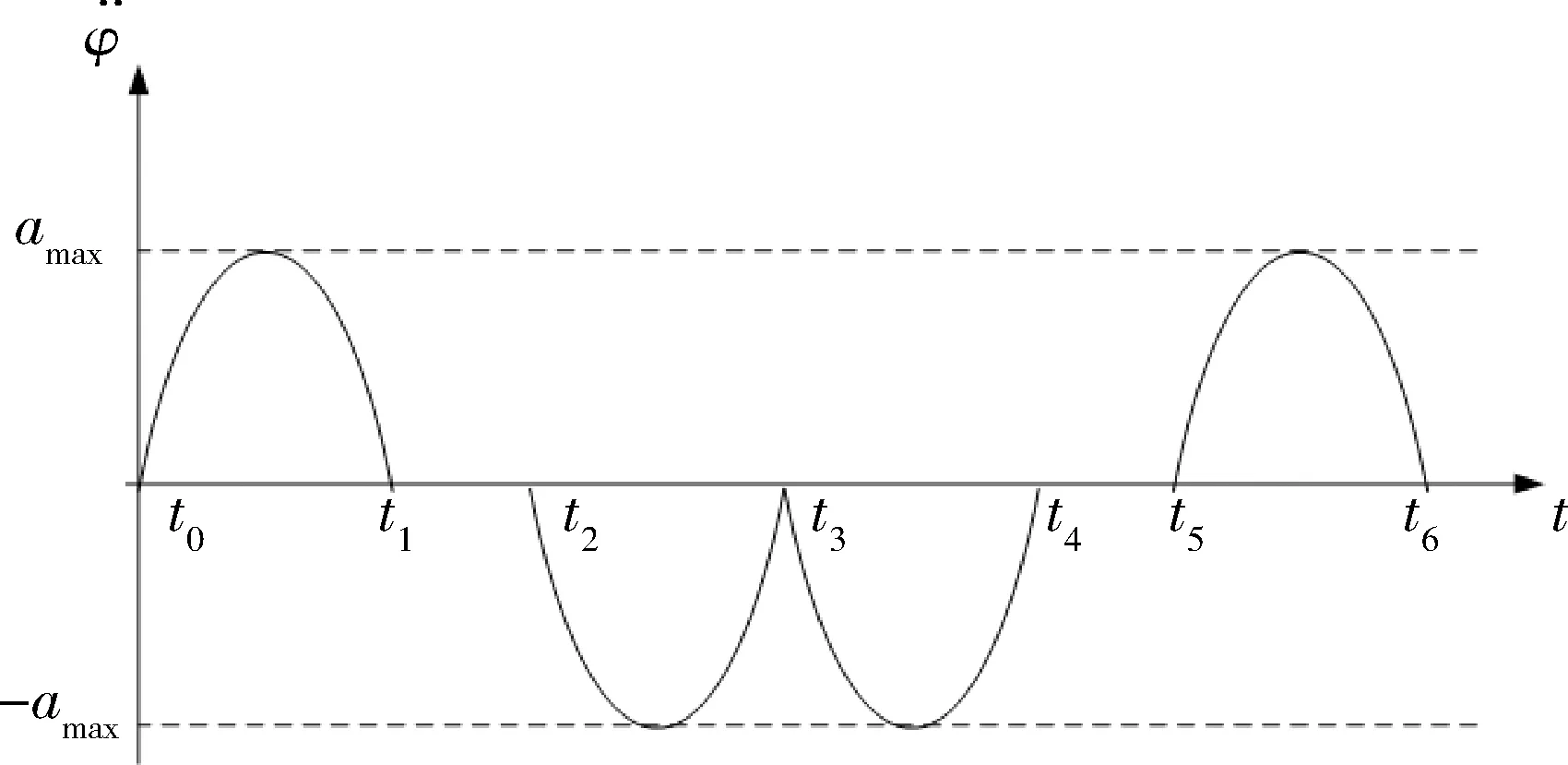
圖3 擺掃中正弦加速度運動加速度曲線
圖3所示為正弦加速度運動1個周期內的角加速度變化曲線,其中,t0~t6為1個周期T;t0和t3時刻衛星的滾動角分別為2個極限值。由于t0~t3,t3~t6兩時段運動特性一致,僅僅是方向相反,因此對t0~t3時段進行分析,并且有t3-t0=T/2。圖中加速段與減速段經歷時間相同,即是:t1-t0=t3-t2。
如圖3所示,t0~t3各個階段的角加速度為:
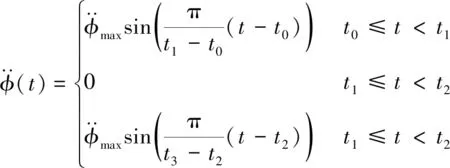
(6)
進一步得角速度和角度關系為:
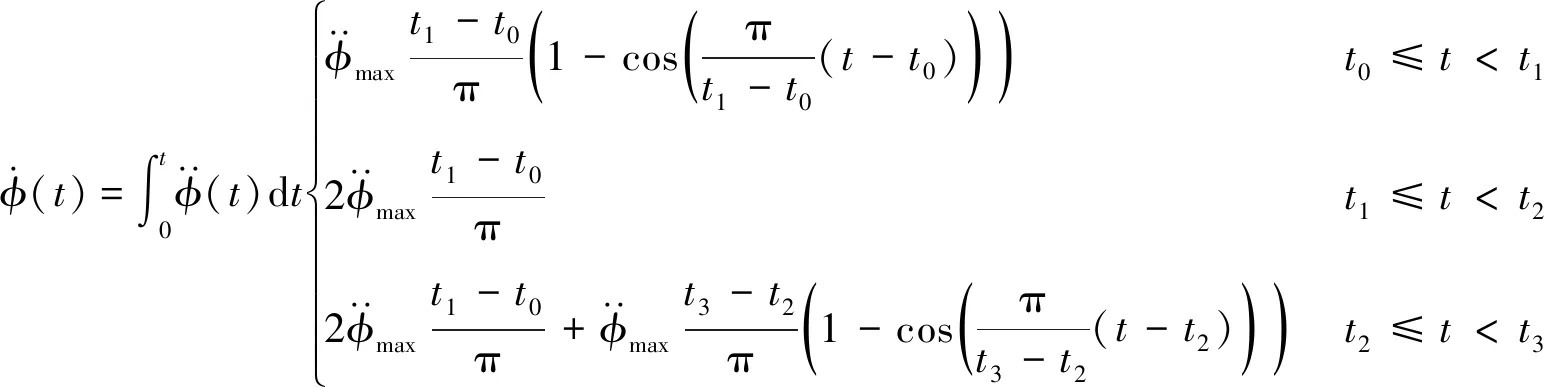
(7)
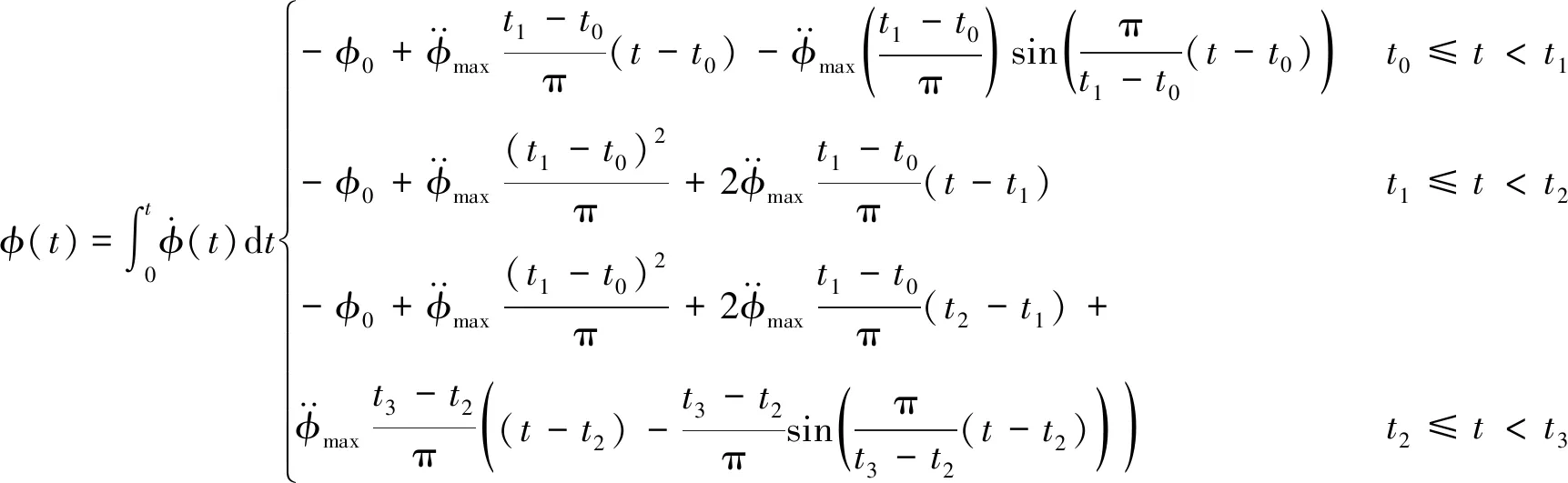
(8)
3 基于剪式CMG的衛星姿態控制
3.1 基于四元數表示的衛星姿態控制
用單位四元數表示衛星的姿態動力學,具有計算量小、避免奇異等優點;通過姿態四元數研究大角度機動問題較為方便。用四元數表示衛星姿態運動學的表達式為:
(9)
其中:
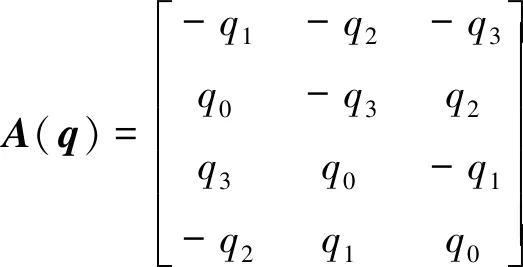
根據歐拉定理,衛星轉動角動量與力矩之間的關系為:
(10)
其中,H為星體角動量;u為控制力矩;Td=[Tx,Ty,Tz]T為衛星受到的干擾力矩總和。干擾力矩來源主要有重力梯度力矩、地磁力矩和太陽光壓力矩等,為簡化計算,本文用1個零均值的高斯分布干擾力矩進行等效。
本文采用原理簡單、應用廣泛且效果穩定的PD控制器進行姿態控制。基于誤差四元數的PD控制器原理為:
Tu=-KpJqev-KdJω+ω×Jω
(11)
轉動慣量矩陣J為一個3×3方陣,由衛星自身質量分布決定,一般可以將其取為對角陣;同樣一般取Kp=diag(kp1,kp2,kp3)為對角陣,Kd=diag(kd1,kd2,kd3),并且Kpi和Kdi均為正數。式中qev為誤差四元數的矢量部分,誤差四元數由當前姿態四元數q和期望姿態四元數qd計算而得。
3.2 剪式控制力矩陀螺操縱律
單框架控制力矩陀螺的示意圖如圖4。
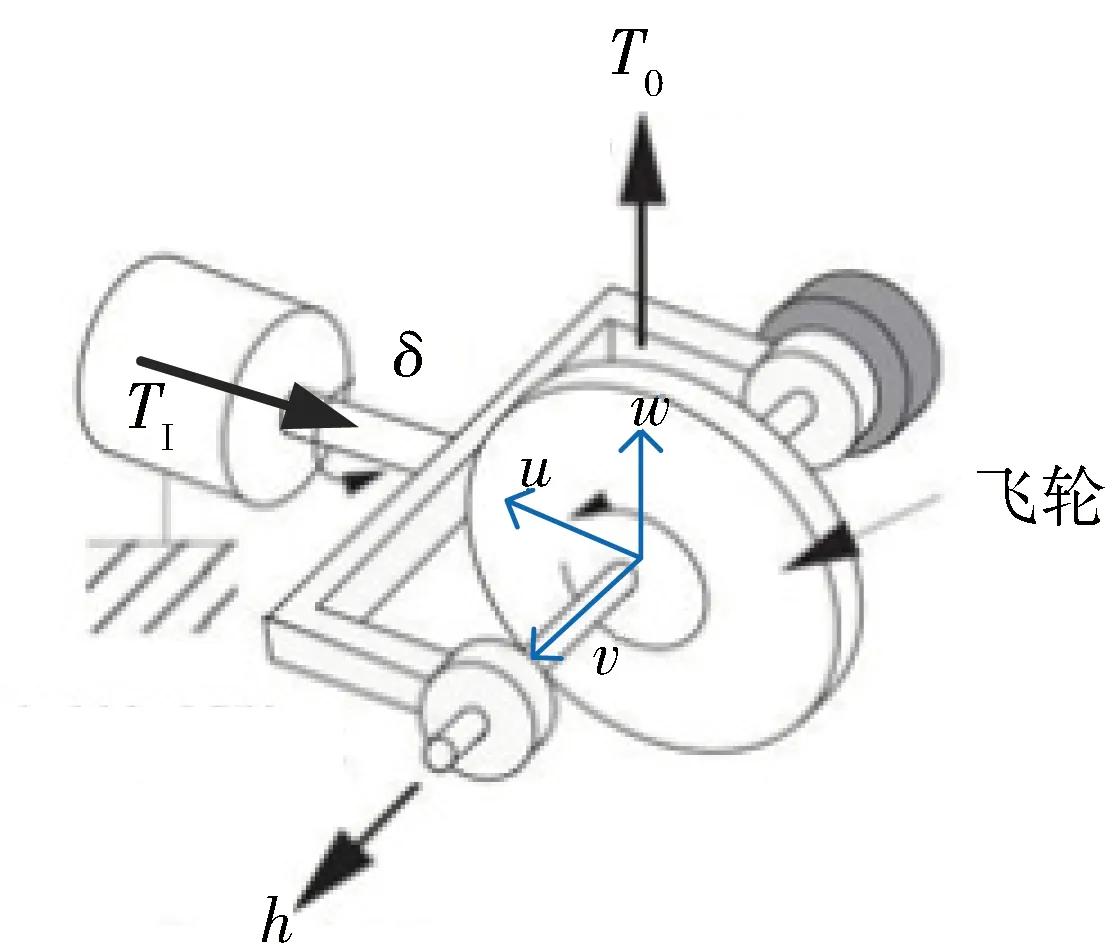
圖4 單框架控制力矩陀螺示意圖
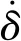
(12)
將一對CMGs進行剪式安裝示意圖如圖5,2個CMG固連在同一個支架上,初始狀態時2個陀螺的角動量共線但方向相反。在輸出力矩時,2個CMG框架角之間始終保持關系δ1+δ2=π。
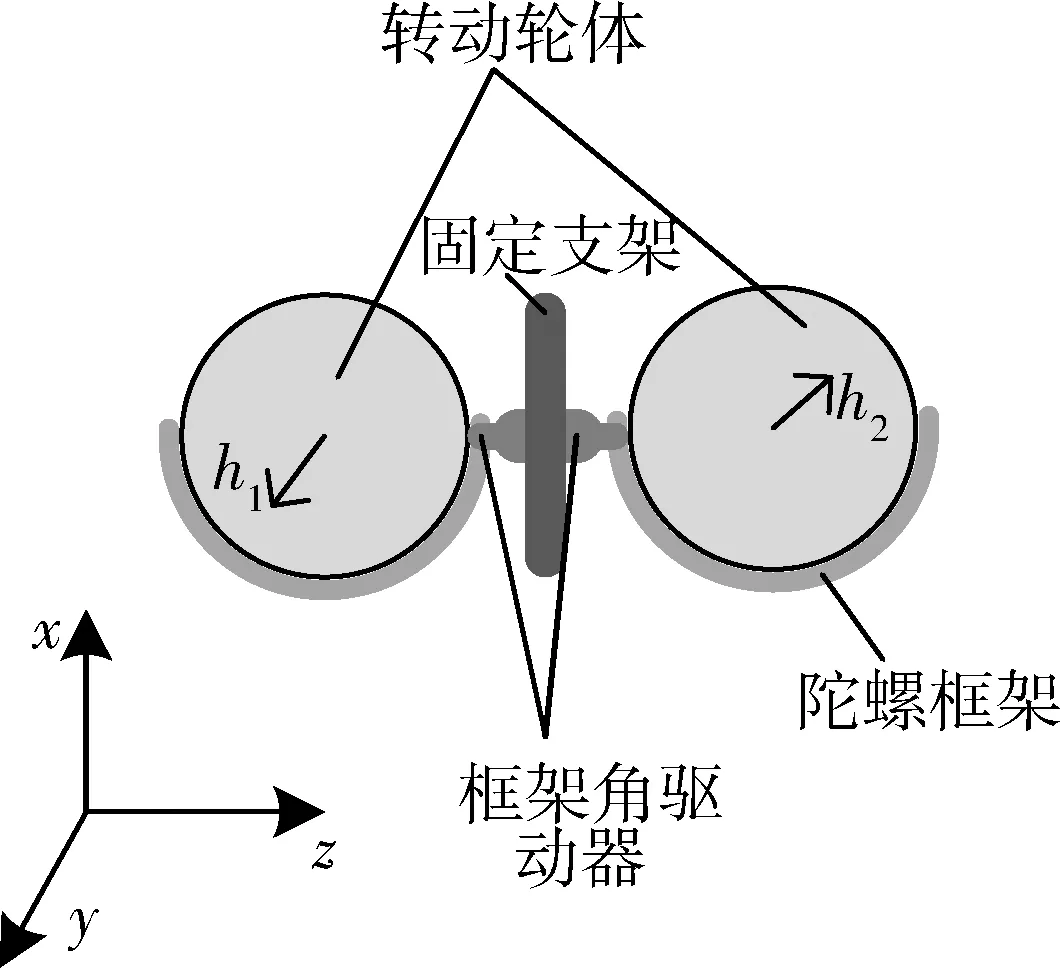
圖5 剪式安裝的CMGs示意圖
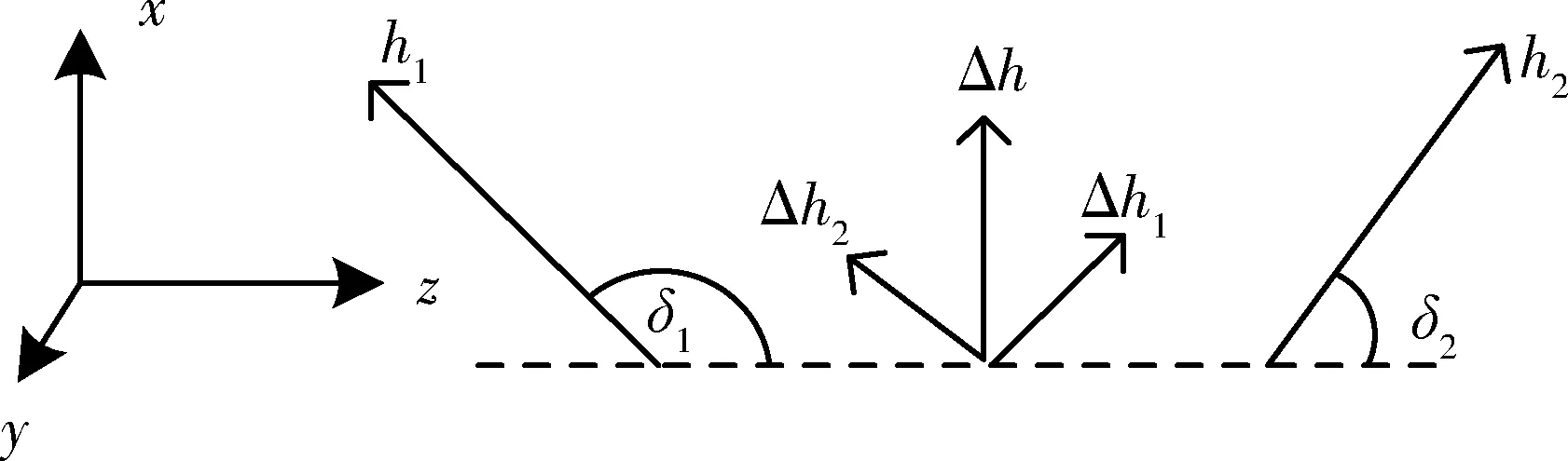
圖6 剪式控制力拒陀螺力矩輸出
圖6為CMGs輸出示意圖,其中δi表示框架角度值,Δhi為角陀螺角動量變化量。由于框架角驅動軸平行于y軸,因此陀螺角動量在xoz平面變化。分析得:
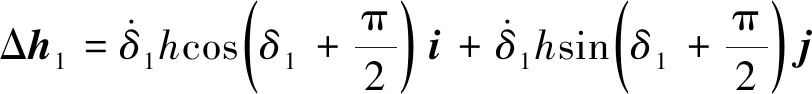
(13)
其中,H1為陀螺轉子角動量大小;i和j分別為x,z軸的單位矢量。由于δ1+δ2=π,則:
(14)
可以看出剪式CMG將z方向的力矩輸出耦合
抵消了,最終的力矩輸出沿x軸方向。
由于衛星需要三軸穩定控制,因此需要在三軸都裝上剪式控制力矩陀螺,共需6個控制力拒陀螺。將6個控制力矩陀螺的框架角表示為δi,i=1,2…,6;其中δ1和δ2的變化輸出x軸力矩,δ3和δ4的變化輸出y軸力矩,δ5和δ6的變化輸出z軸力矩。類比式(11),得到如下關系:
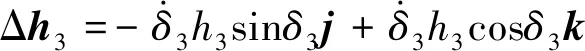
(15)
由于剪式控制力矩陀螺滿足約束:h3=h4=H2,h5=h6=H3,將CMG系統的總角動量變化率和框架角速度之間的關系表示為式(16):為保證矩陣的求逆,附加約束條件δ1+δ2=δ3+δ4=δ5+δ6=π,將雅克比矩陣寫成方陣形式,獲得關系如式(17):
(16)
(17)
4 衛星擺掃運動控制仿真
由式(2)得擺掃時一個周期為T=14.2s,系統刷新速率為Δt=0.05s,衛星的轉動慣量為:
PD控制參數為
干擾力矩Td服從均值為0、標準差為0.05的正態分布。由于實際中橫滾角是主要機動方向,對于CMGs力矩輸出要求較大;而俯仰角和偏航角上僅需要調節由誤差引起的姿態擾動,對于CMGs力矩輸出要求小,因此選用更小輸出的CMG,能夠減小執行器質量,降低系統功耗。
仿真時設定CMG轉子角動量為:
H1=1.3kg·m2/s
H2=H3=0.25kg·m2/s。
取2個擺掃周期作為仿真對象,分別對于恒角加速度運動和正弦角加速度運動時的衛星姿態運動參數、CMGs輸出力矩以及框架角速度變化情況進行分析。
a)按照恒角加速度運動進行垂軌擺掃的matlab仿真結果如圖7~10所示
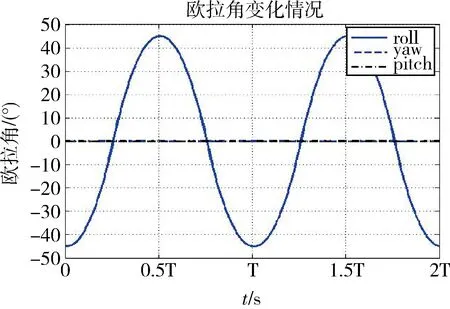
圖7 恒角加速度垂軌擺掃歐拉角變化情況
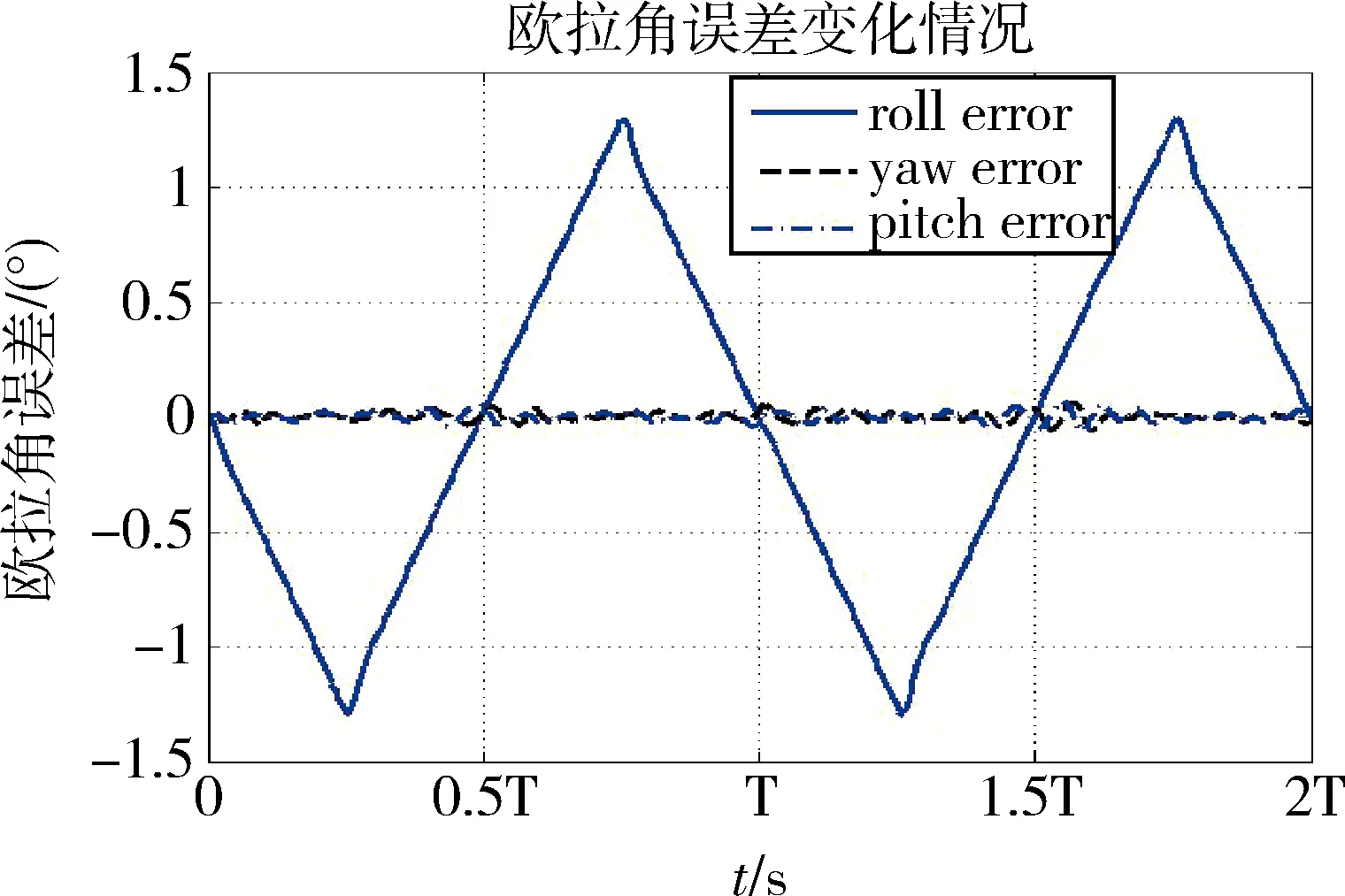
圖8 恒角加速度垂軌擺掃歐拉角誤差
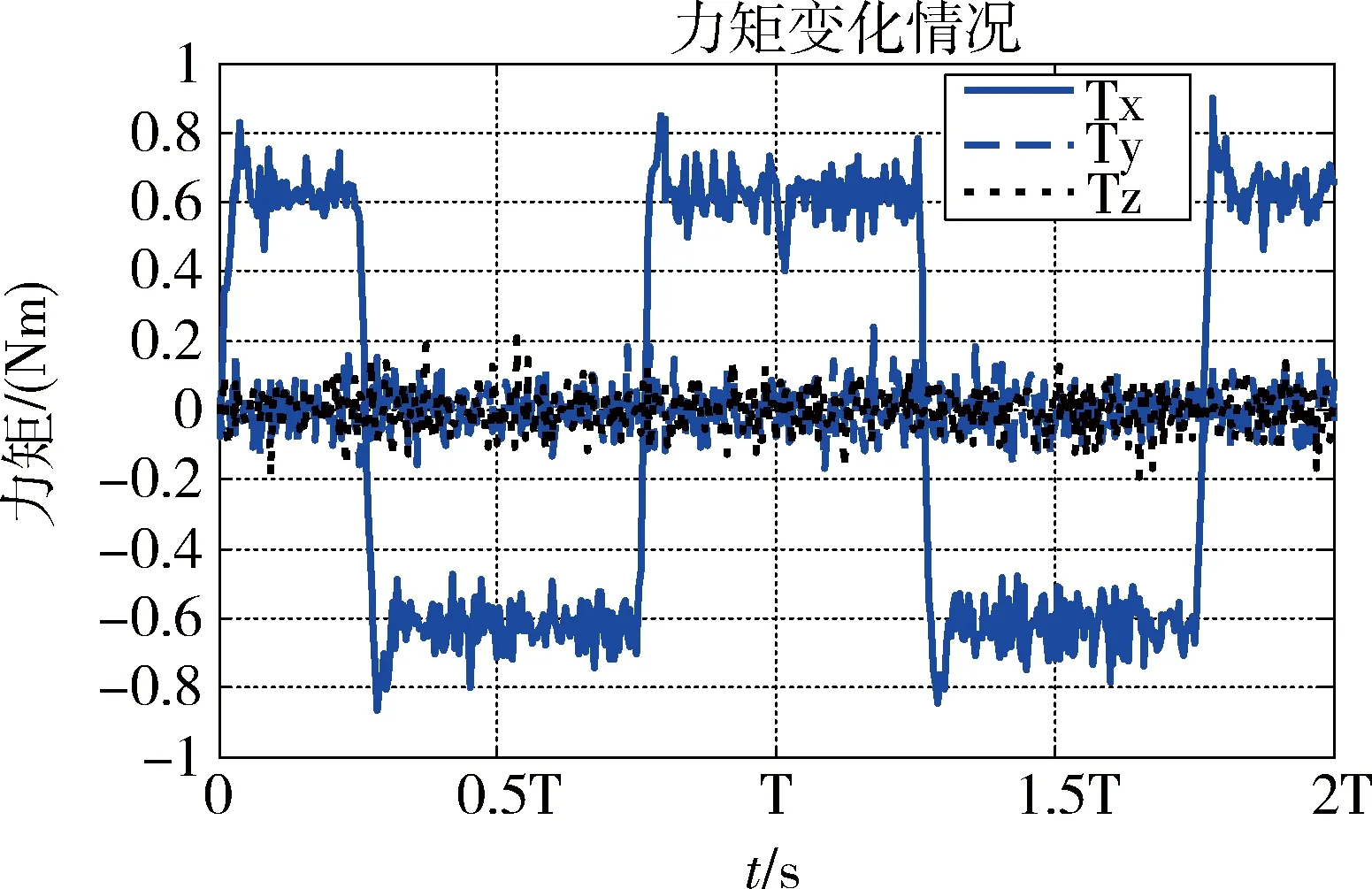
圖9 恒角加速度垂軌擺掃控制力拒
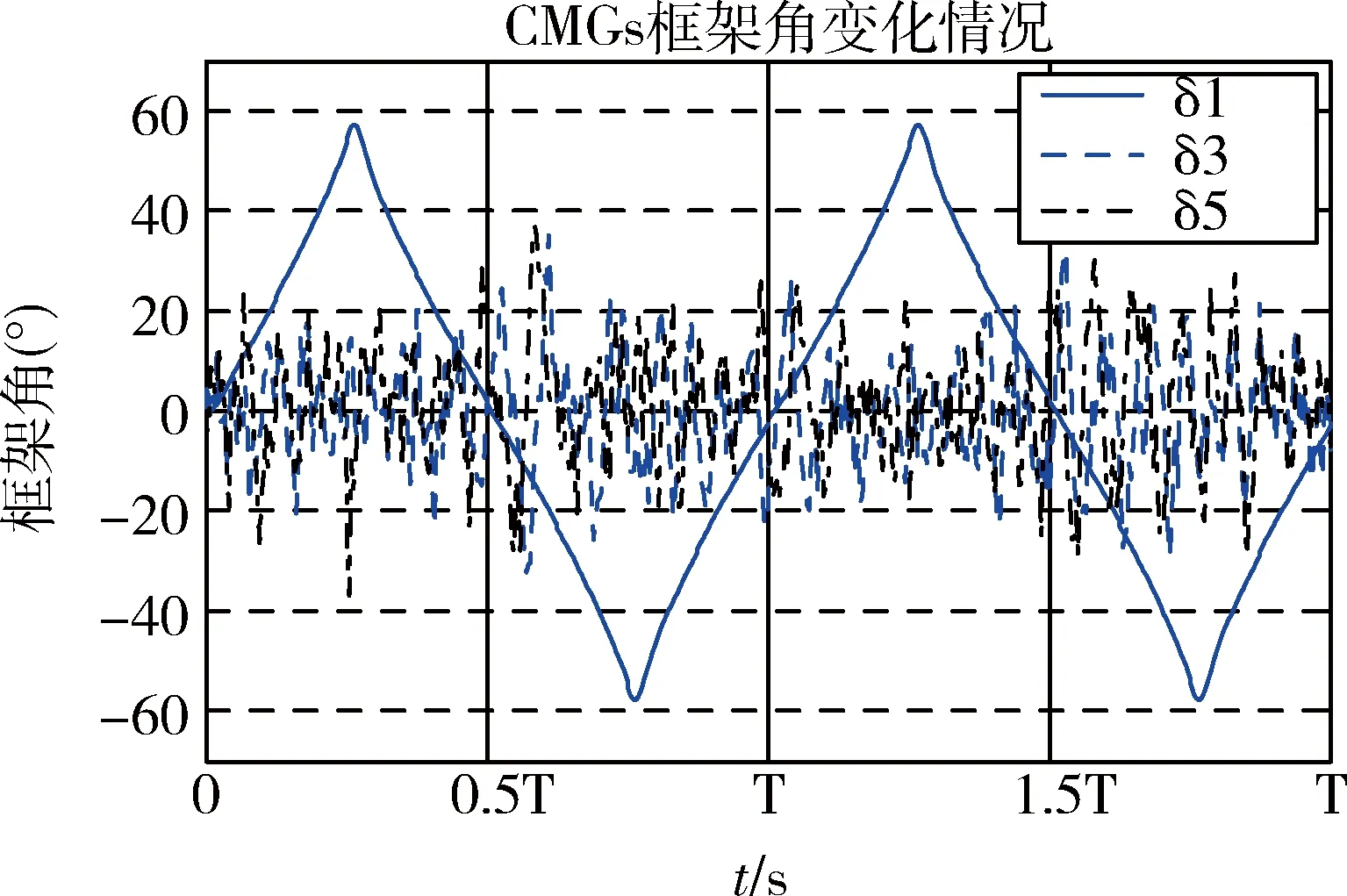
圖10 恒角加速度垂軌擺掃陀螺框架角
在選定的仿真參數下,滾動軸姿態誤差最大值為1.28°。對于x軸向控制力拒,其絕對值均值為0.61N,其最大值為0.91Nm;y軸向控制力矩絕對值均值為0.051N,最大值為0.19N;z軸向控制力矩絕對值均值為0.053N,最大值為0.16N。x軸上的控制力矩陀螺框架角工作空間為-57.9°~57.1°;y軸上的控制力矩陀螺框架角工作空間為-36.5°~38.6°;z軸上的控制力矩陀螺框架角工作空間為-38.7°~37.9°。
b)按照正弦角加速度轉動進行垂軌擺掃的matlab仿真所得結果如圖11~13所示。

圖11 正弦角加速度垂軌擺掃歐拉角誤差
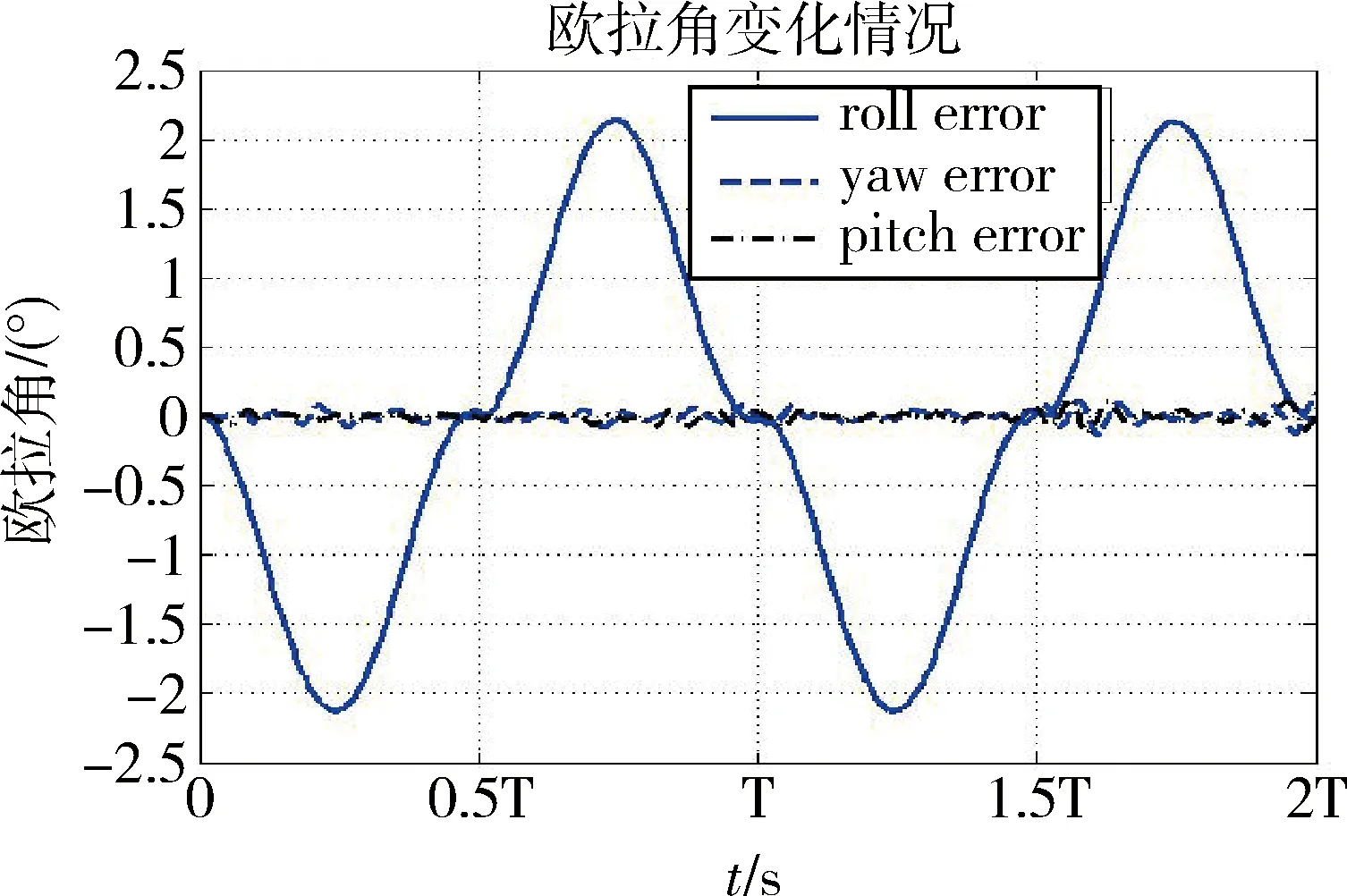
圖12 正弦角加速度垂軌擺掃歐拉角誤差
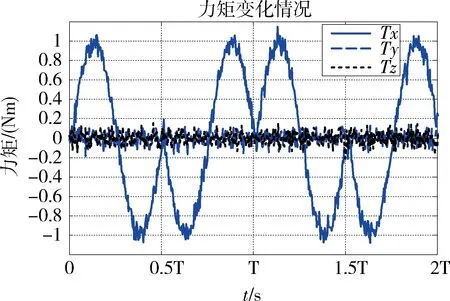
圖13 正弦角加速度垂軌擺掃控制力矩變化情況
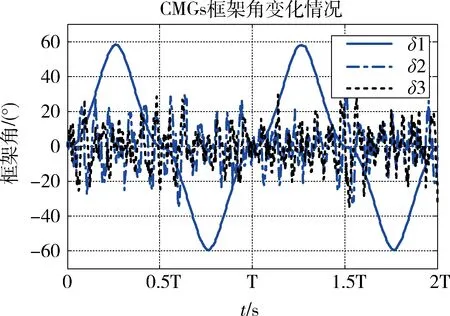
圖14 正弦角加速度垂軌擺掃陀螺框架角
在選定的仿真參數下,滾動軸姿態誤差最大值為2.12°。對于x軸向控制力拒,其絕對值均值為0.62N,其最大值為1.13Nm;y軸向控制力矩絕對值均值為0.052N,最大值為0.19N;z軸向控制力矩絕對值均值為0.054N,最大值為0.22N。x軸上的控制力矩陀螺框架角工作空間為-59.2°~58.3°;y軸上的控制力矩陀螺框架角工作空間為-37.5°~36.9°;z軸上的控制力矩陀螺框架角工作空間為-38.2°~34.2°。
正弦角加速度姿態機動的優勢在于能夠有效減小衛星振動,但是從仿真結果來看,正弦角加速度姿態機動的角度誤差要大于恒角加速度姿態機動的誤差,并且CMG的最大力矩輸出要求也更大。因此在對振動抑制沒有特殊需求時,選擇恒角加速姿態機動效果更好。
5 結論
針對大范圍持續監測任務,設計了基于剪式CMGs低軌衛星垂軌擺掃探測姿態控制系統。仿真結果表明選用的剪式控制力矩陀螺框架角在允許范圍內變化,擺掃期間沒有出現奇異,控制系統能夠實現對預定軌跡的穩定跟蹤,完成大范圍探測任務。

