巖石類介質侵徹效應的理論研究進展*

李 杰，程怡豪,2，徐天涵，王明洋,3

（1. 陸軍工程大學爆炸沖擊防災減災國家重點實驗室，江蘇 南京 210007；2. 陸軍工程大學野戰工程學院，江蘇 南京 210007；3. 南京理工大學機械工程學院，江蘇 南京 210094）

侵徹效應是指彈體高速撞擊靶體產生的破壞效應，若彈體穿透金屬靶體，人們又習慣稱為穿甲。天然巖石具有強度高、抗侵徹性能好的特點，因此重要的地下防護工程總是盡可能選址于強度高、完整性好的天然巖體中，許多防護工程也會利用塊石作為遮彈層的主要材料[1-3]。因此，彈體對巖石侵徹效應歷來是防護工程領域關注的關鍵科學問題之一，其往往體現為相互“矛盾”的兩方面：一方面，武器裝備研究人員通過提升彈體速度、優化彈體結構和發展串聯戰斗部等手段增加侵徹深度[4]；另一方面，防護工程研究人員則需要合理設計以天然巖層為基礎的安全防護層厚度，通過增加掩體埋設深度、改進防護層材料和配置方案等手段提高防護工程的抗侵徹能力[5-7]。

侵徹效應的研究最早可以追溯到19 世紀以前[1,8]，在20 世紀取得長足進展。尤其最近三十年，因GBU-28 等精確制導鉆地武器在幾場局部戰爭中的杰出表現[1,4]，引起國內外學者的高度關注，將巖石中侵徹效應的研究向前推進了一大步。從研究手段上看，侵徹效應的研究主要有試驗、數值模擬計算及理論分析等手段。早期的研究主要是通過對大量實驗數據的總結，歸納出經驗或半經驗的計算公式，具有簡單直接的特點，在世界各國有關防護結構的設計規范或計算手冊中得到廣泛應用[8-11]，其缺點在于適用范圍狹窄，這些公式在實驗特定的范圍之內具有較高的準確性，但是介質的特征參量和彈體的侵徹速度、幾何尺度等一旦超出實驗范圍，就會造成預測預報的偏差[1,11-12]。近三四十年來，利用大型仿真程序進行侵徹數值計算的研究獲得快速發展[5,12-15]，數值模擬的誘人之處在于能提供彈體和靶體內部響應的詳細信息，這些信息通常是在實驗中也難以觀察到的，然而其計算結果往往受本構模型與相關參數選取的限制，具有較強的人為性。侵徹問題本質上是一種復雜的沖擊局部問題，主要取決于撞擊物（彈體）與被撞擊物（靶體）的撞擊速度、撞擊姿態、材料性能和彈靶雙方的幾何與結構特性[16-18]。為揭示問題實質，根據彈靶的幾何和物理特性，以問題的主要影響因素為切入點，建立具有明晰的物理力學意義的簡化理論模型仍然具有十分突出的理論意義和工程價值。

傳統鉆地武器普遍采用高硬度合金且對地打擊速度普遍不超過1 km/s，因此經典巖石侵徹理論中常常將彈體假設為剛性彈，理論分析的核心在于彈體阻力函數，剛性侵徹是侵徹理論研究比較成熟的部分。目前，隨著科技的發展，彈體的發射速度更高，試驗證實[19-30]，當彈體速度由一般侵徹速度（＜900 m/s）向高速侵徹（1 200～1 700 m/s）轉移時，在侵徹過程中會發生彈體的質量侵蝕，嚴重影響了彈體的侵徹性能，甚至出現侵徹深度的“逆減”效應。近年來高超聲速技術已經從概念和原理探索階段進入了實質性的技術開發階段，外軍正在研發的超高速動能武器對地打擊速度3 000～5 000 m/s，此時的侵徹問題將具有顯著的超高速碰撞問題的特點，即侵徹過程是一個由動能急劇釋放引起的極端高溫高壓過程，不僅會發生侵徹，還會引起顯著的成坑效應并觸發強烈的地沖擊效應，其作用范圍可遠超侵徹深度，其破壞效應接近于淺埋爆炸[13,15,31-34]，其侵徹機理與破壞模式與常規侵徹問題存在顯著差別。當前對高速和超高速彈體對巖石的侵徹效應及其內在機理研究尚不十分充分，這也是當前理論研究的熱點問題。

本文中圍繞大速度范圍內巖石類介質的侵徹效應經驗公式、侵徹理論模型、成坑效應和地沖擊效應的研究成果，綜述國內外學者的相關理論研究成果，并對目前研究中尚有待解決的問題和下一步的研究方向進行展望。需要說明的是，為達到最佳的侵徹效果，鉆地武器一般具有細長的殼體外殼，除非特別指出，本文中主要論述理想垂直入射條件下長桿彈對巖石厚靶的一維侵徹問題，不考慮貫穿問題和斜侵徹問題，同時，為了便于介紹理論模型的發展歷程，也會涉及到部分金屬、混凝土介質的侵徹理論。

1 侵徹效應經驗公式

鉆地武器侵徹巖石深度的研究是防護工程領域關注的問題之一，由于沖擊侵徹現象的復雜性，在很長時期內，該問題的實用計算都是采用以彈道試驗為基礎的經驗公式。建立經驗公式的方法大體有兩種：一種是直接對試驗數據進行回歸分析建立的經驗公式，又稱純經驗公式；另一種是預先假定作用在彈體上的阻力變化規律，運用運動方程推導出計算公式，再利用試驗數據資料修正公式中的常數，這種方法建立的公式稱為半經驗半理論公式。在防護工程領域，當前應用較多的巖石侵徹經驗公式主要包括美國圣迪亞國家實驗室（SNL）的Young 公式[8]、美國陸軍水道實驗站（WES）的Bernard 公式[9]（包含三個版本）和蘇聯的別列贊公式[10]等。

（1）Young 公式形式為：

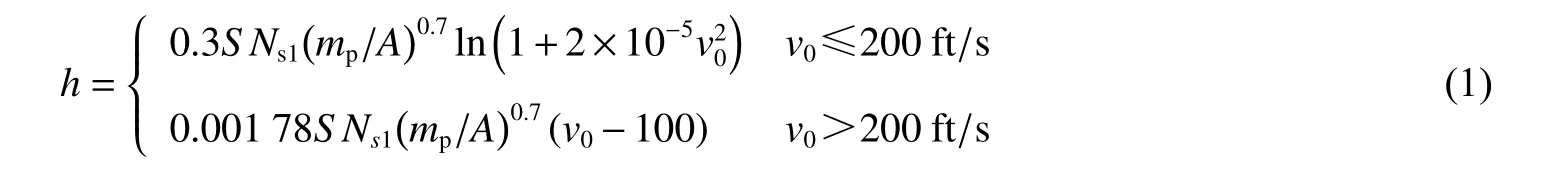
式中：所有參數均采用英制單位，h 為侵徹深度，S 為可侵徹性指標， S = f(fcQ)與巖石無側限抗壓強度fc和 巖石質量 Q （巖石完整性程度）有關，Ns1為彈頭形狀系數，mp為彈體質量，A 為彈體截面積， v0為彈體初始撞擊速度。

（2）Bernard 公式的三個版本的主體分別為：

（3）別列贊公式的形式為：

式中：λ1為彈形系數，λ2為彈徑系數， d為彈體直徑，α 為命中角（即彈體軸線與目標表面法線方向夾角），Kα為彈體偏轉系數，Kq為靶體材料的侵徹系數（主要與材料無側向抗壓強度有關）。

從參數選擇看，以上公式均以一定的方式考慮了彈體質量、撞擊速度、彈體截面積（或彈體直徑）和巖石無側限抗壓強度，但不同之處在于：

（1） Young 公式和Bernard 公式均考慮了巖石的完整程度的影響，但別列贊公式未考慮，這導致后者無法合理預測抗壓強度相同但風化程度不同的巖石的侵徹深度。

（2） Bernard 公式（III）相對于其早先版本最重要的修正之一是增加了對彈頭形狀的考慮。

（3） 別列贊公式的主要特色在于考慮了非垂直入射和彈體偏轉的影響，這是其他公式所未考慮的；但是別列贊公式對靶體性質考慮較為簡略，甚至沒有考慮巖石密度的影響。

從預測效果看[35]，Young 公式和Bernard 公式比較接近，別列贊公式的預測效果較以上公式均明顯偏大，其主要原因是別列贊公式的實驗數據來源于對地表風化巖石的原位侵徹實驗，因此在相同條件下其侵徹深度較深，從防護工程設計角度而言偏于安全。

經驗公式能反映問題的主要影響因素，使用簡便、計算可靠度較高，因而目前各國有關防護結構的設計規范中，基本還是采用經驗公式計算彈體的侵徹深度，其缺點在于試驗費用高、適用范圍窄，公式只能反映彈體初始情況與最終結果間的關系，不能說明彈靶相互作用機理，不能準確分析侵徹過程中彈體所受到的阻力。

此外，需要指出的是，以上公式均默認相同條件下侵徹深度隨著彈體撞擊速度的增加而增加，但實際情況是，當彈體打擊速度足夠高時，存在一個侵徹深度隨打擊速度增加而急劇下降的階段，與之伴隨的是彈道偏轉和彈體的侵蝕破壞，當打擊速度進一步增加時，由于彈靶接觸面的劇烈壓縮作用使介質材料破壞、融化，侵徹深度隨著打擊速度的增加而緩慢增加并有趨于流體動力學極限的趨勢[19-20,31, 36-37]，在長桿彈侵徹鋁靶、混凝土靶的中也發現了類似的轉變現象[21-29,38-41]。可見，式(1)～(3)的適用條件主要局限于彈速不高、彈道偏轉不大、彈體變形不顯著的情形，不適用于超高速侵徹問題。

2 不同打擊速度下侵徹效應的理論模型

2.1 對速度分區的討論

從桿形彈體對多種密實介質（巖石、混凝土和鋁等）的侵徹實驗結果看[19-26,36-41]，在近似理想垂直入射條件下，隨著撞擊速度增加，彈體均將經歷從變形可忽略的階段（僅有少量質量損失）向侵蝕階段（即彈體長度嚴重縮短）的轉變，侵徹深度也將經歷“迅速增加-逆減-緩慢增加-趨于流體動力學極限”的過程，不同過程的物理機理不同。由于撞擊速度是決定侵徹效應的首要因素，在速度分區問題上許多學者提出了許多建議。

Forrestal 等[41]通過鋼桿彈在0.5～3.0 km/s 范圍內侵徹鋁靶的試驗發現，隨撞擊速度提高，彈體經歷了從剛體彈侵徹到侵蝕彈侵徹的轉變，伴隨侵深大幅下降的現象，Chen 等[39]根據對前述侵徹速度下彈體失效機理進行分析，提出了“剛性彈侵徹-半流體侵徹-流體侵徹”三階段劃分模型，并利用撞擊函數I 給出了剛性彈侵徹上限和半流體侵徹下限 Ic2的臨界閾值（見圖1）。由侵蝕彈向半流體侵徹轉換的臨界值 Ic為：

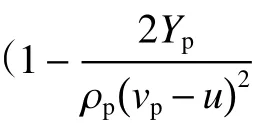
圖 1 鋼桿彈撞擊鋁靶機理分區[39]Fig. 1 Schematic of penetration of steel projectiles into aluminum targets[39]

以上主要通過彈體的響應對超高速侵徹問題進行分區，更加完善的速度分區需要綜合考慮靶體的響應。巖石介質是由尺寸、形狀和礦物成分各不相同的許多顆粒連接在一起而組成的集合體，顆粒的排列方式不規則并且存在有缺陷。巖石構造缺陷水平包括微觀上的原子層次（包括空缺和位錯），細觀上的構造缺陷（包括顆粒內裂縫、沿過多個顆粒的粒間裂縫和沿粒界的裂縫、構造上邊界碎片的分層、夾雜物等），甚至宏觀上的裂隙、節理以及層理等，其力學性質受材料性質、材料微結構、荷載性質、加載速率及材料應力歷史和加載路徑等各種因素的制約，傳統的彈塑性力學本構難以準確描述。Shemyakin[47-49]研究指出在強爆炸沖擊作用近區巖石行為由彈性狀態向塑性狀態轉變時，不是轉向理想的塑性狀態，而是轉向顯著增強的塑性狀態，這種增強的本質在于受限內摩擦。對巖石介質侵徹速度的準確劃分需要準確了解沖擊壓縮狀態下巖石介質的動力學行為及可能的力學狀態。Ahrens 等[50]基于沖擊波響應過程的研究，認為壓縮作用下巖石介質的動力響應過程可劃分為五個階段（圖2）：0，彈性階段；1，塑性狀態；2，低壓力狀態；3，混合狀態，4，高壓力狀態。在彈性、塑性、低壓力階段，材料的強度起主要作用，表現為固體屬性；在高壓力狀態，材料的體積壓縮起主要作用，表現為流體動力學屬性，可以認為達到超高速侵徹機制的臨界條件是體積壓縮性在阻力項中占主導地位。

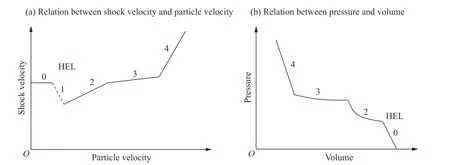
圖 2 巖石的動力壓縮曲線[50]Fig. 2 Dynamic compression curves of rock[50]

王明洋等[32]在系統研究巖石介質侵徹近區動態可壓縮行為的基礎上，提出了流體彈塑性內摩擦侵徹模型，認為隨著打擊速度的提高，彈靶近區相互作用壓力增大，靶體的力學狀態發生從低應力固體狀態、內摩擦擬流體狀態至高應力流體狀態的改變，在不同狀態區巖石的固體、流體屬性分配份額不同，導致巖體的應力波狀態、應力波衰減軌跡、應力應變狀態等力學行為發生顯著變化，具體如表1[51]所示。

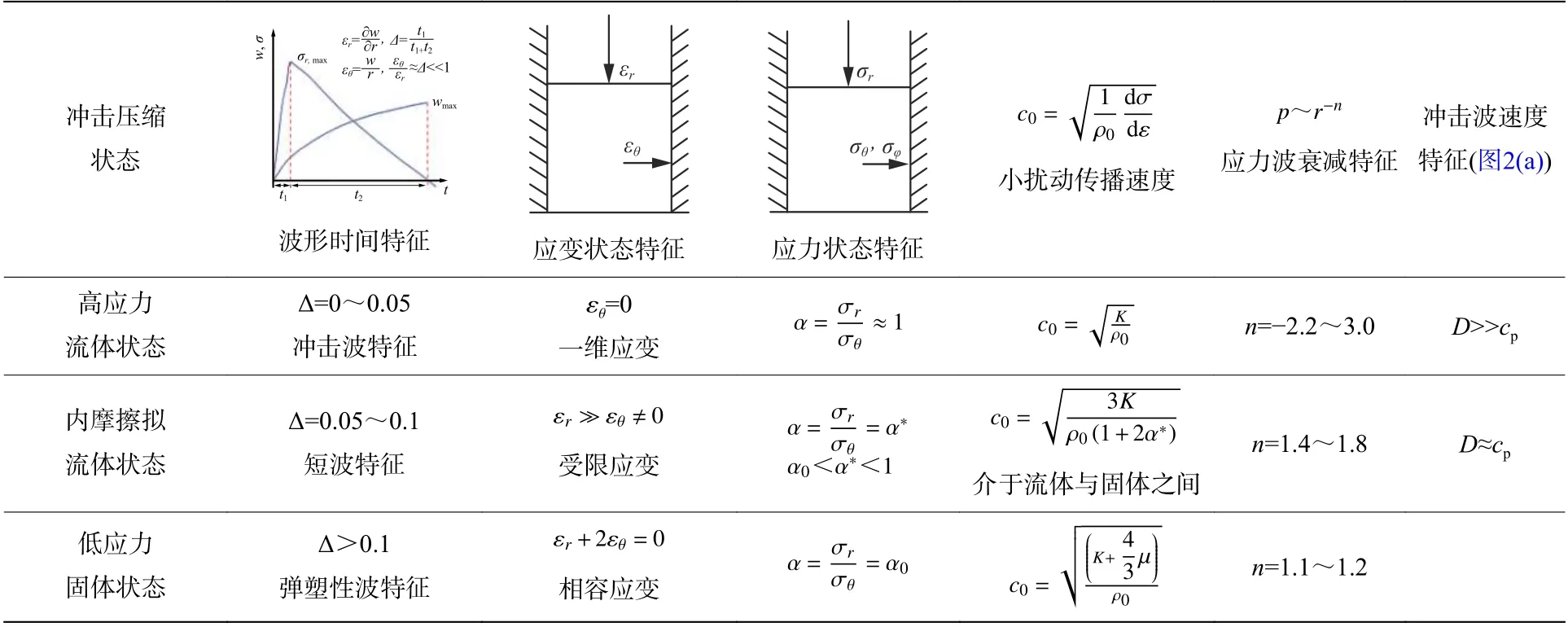
表 1 沖擊壓縮作用下典型硬巖分區行為特征[51]Table 1 Dynamic behaviors of hard rock in different ranges under shock compression[51]

表1 數據與圖2 基本一致，表1 中低應固體狀態對應圖2 階段2，內摩擦擬流體狀態對應圖2 階段3，高應力流體狀態對應圖2 階段4。隨后，王明洋等[32]根據不同彈體速度打擊下靶體體積應變曲線p/Ht偏離線性、剪切強度 τ/Ht趨近于 τp/Ht（ 見圖3）以及側壓力系數 α趨近于1（見圖4）的程度，將撞擊速度大致分為三個區間：

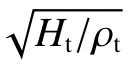
圖 3 侵徹速度界定及介質壓縮狀態Fig. 3 Definition the scope of penetration velocity and medium compression state

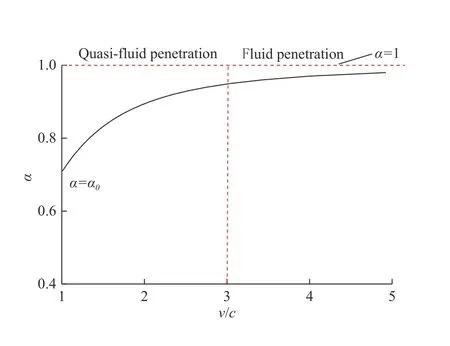
圖 4 v /c與α 關系曲線Fig. 4 Curve between v /c and α

高速或超高速打擊條件下，彈體速度 vp與 彈靶接觸面處靶體巖石質點運動速度 v 有以下換算關系[32]：

式中：ρp和ρt分別為彈體和靶體密度，這樣，結合公式(5)～(6)就可以判斷不同的彈體打擊速度下靶體介質所處的力學狀態。

由彈體變形和侵蝕所導致的侵深逆減現象可能出現在靶體的低應力彈塑性區和內摩擦擬流體區，具體視彈體形狀、彈靶材料形狀等因素制約。根據高強合金鋼對花崗巖等典型硬巖的侵徹試驗結果[19]（見圖5），一般彈體在靶體的低應力固體區即發生侵蝕，這樣，典型硬巖可分為：剛性彈固體侵徹（圖5 中區域I）、侵蝕彈固體侵徹(區域II)、擬流體侵徹(區域III)、流體動力學侵徹四個階段，與Chen 等[39]分區不同，此處綜合考慮了彈體和靶體的力學狀態，剛性彈侵徹、侵蝕彈侵徹主要針對彈體狀態，固體侵徹、擬流體侵徹、流體動力學侵徹則主要針對靶體力學狀態。

圖 5 花崗巖侵徹實驗結果（撞擊速度1～2.5 km/s）[19]Fig. 5 Experimental results of penetration into granite targets with impact velocity from 1?2.5 km/s[19]

2.2 剛性彈體侵徹理論

剛性彈體侵徹理論的成果最豐富、發展最成熟，主要包括：空腔膨脹理論、微分面力法、速度勢理論、滑移線法等[1,52-54]。其中，空腔膨脹理論的固有特性決定了其不同彈頭形狀、不同靶體材料均有較好的適應性，近十多年來，在Forrestal 等[55-56]的研究成果的基礎上，研究人員通過對材料本構關系的修正，即將材料體積變形方程從不可壓縮向躍變壓縮、線性壓縮、非線性壓縮發展，強度模型則從理想彈塑性向線性硬化、冪次硬化、壓力相關強度準則、分階段強度準則發展并可考慮脆性斷裂效應，使得空腔膨脹理論得到了新的推廣[57-65]。

空腔膨脹理論應用于彈體侵徹分析中的關鍵是根據質量和動量守恒方程建立空腔膨脹速度與徑向應力的關系，進而計算彈體受到的侵徹阻力，為了便于計算，通常將侵徹阻力寫成如下顯式形式：

式中：v是瞬時侵徹速度，Fz是侵徹阻力，α、β、γ 分別為速度二次項、一次項和零次項系數。特別地，當β=0 時，式（7）被稱為Poncelet 型阻力函數并得到了最廣泛的應用，其經典形式為Forrestal 等[65]提出的：

式中：Rt是材料的固有阻力，N*是彈頭形狀系數。對于混凝土，Rt近似滿足如下經驗關系：

式中：fc為混凝土單軸抗壓強度。

在滿足Poncelet 型阻力函數時，由空腔膨脹理論得到的典型侵徹深度表達式為：

式中：K1和K2為靶體材料密度、強度和彈頭形狀決定的參數。值得注意的是，Frew 等[20]、張德志等[36]分別采用式（8a）對石灰巖和花崗巖侵徹實驗結果進行擬合，發現Rt與彈體撞擊速度和彈體尺寸均密切相關，這說明式（8a）并不完全適合巖石介質。錢七虎等[51]、王明洋等[66]采用應力短波條件下的內摩擦侵徹理論得到了彈體阻力的表達式，并根據參數分析發現恰恰是Poncelet 型阻力函數所忽略的速度線性阻力函數在硬巖介質的中高速侵徹過程中起決定性作用，因此侵徹深度與撞擊速度之間近似滿足線性關系，這與經驗公式較為一致。

2.3 變形彈侵徹計算理論

實驗研究表明，高速侵徹條件下，彈體可以在未出現侵蝕和顯著質量損失的情況下發生磨蝕、鈍化、彎折等情況，嚴重影響彈道的穩定性，引起侵徹深度陡然降低。上述情形被歸結為變形彈侵徹問題，此時仍然可以采用牛頓第二運動定律描述彈體運動，但必須計及彈頭的磨蝕和質量的損失。

在彈體變形機理方面，何麗靈等[27,67]、Guo 等[68]研究了侵徹混凝土時彈體磨蝕和質量損失的物理過程。何麗靈等[69-70]引入修正系數表征熔化彈體表面材料脫落和靶中骨料硬度對彈體質量損失的影響，給出了質量增量表達式，計算時，每個時步內認為彈頭形狀保持不變，計算完成后，再根據彈頭質量增量確定彈頭形狀，計算認為彈頭質量損失對侵徹影響可以忽略，主要是彈頭形狀影響侵徹深度。鄭浩[71]采用彈靶分離的方法和修正后Archard 磨損彈體侵蝕模型，建立了彈體頭部鈍化演變差分計算方法，得到了不同撞擊速度下彈體頭部形狀。楊陽[72]利用量綱分析推導了考慮骨料硬度的彈體侵徹混凝土靶體的質量損失無量綱公式。

在侵徹模型方面，Zhao 等[28]指出隨著初始撞擊速度的增加，彈頭將被磨損，并且明顯地從截卵形彈頭變為半球形，甚至更鈍的形狀，據此根據試驗結果建立了彈頭形狀系數與瞬時侵徹速度的關系和彈體侵徹過程中的質量，最后采用剛性彈侵徹計算方法得到變形彈侵徹計算模型，并發現在考慮磨損效應后侵徹深度將在某一撞擊速度下出現極值，大致對應于實驗中發現的侵徹深度突降臨界速度。

Lan 等[73]假設撞擊的瞬間，彈體頭部立即發生變化（見圖6），并且橫截面積保持Ad不再變化，且變化后的頭部仍然保持球形，整個已變形區域的質點速度均為 vm，在界面處存在質點速度和橫截面積間斷，且壓力在界面處均勻分布，開坑截面積保持不變，得到了變形彈侵徹時彈尾速度與侵徹速度的關系：

式中：au由試驗結果確定， v0為 初始撞擊速度， vg為從剛性彈侵徹進入變形彈侵徹的臨界速度。最終得到了變形彈階段的侵徹深度計算公式：

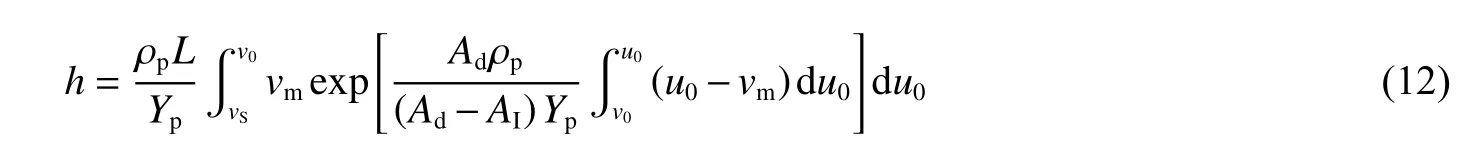
式中：L 為彈體長度。從以上研究成果總體來看，目前彈體變形過程中質量磨蝕的影響還未定論，彈頭鈍粗與質量磨蝕對侵徹的影響程度還需明晰，彈頭鈍粗的程度還很大程度上依賴于試驗擬合結果。彈道穩定性研究方面，還未見考慮彈體磨蝕引起的彈道偏移的定量理論研究成果。作者及其同事在花崗巖侵徹實驗中未觀察到彈體墩粗的現象(見圖7)[19]，據此認為侵徹深度的減小主要是彈體質量損失引起的（圖5 中區域II 彈體質量急劇降低伴隨著侵徹速度的急速逆轉），通過引入彈體質量損失函數建立了變形彈侵徹理論[31]，這部分介紹詳見2.5.2 節。

圖 6 變形彈計算假設[73]Fig. 6 Assumption of deformable projectile[73]

圖 7 不同速度侵徹后回收彈體的形態[19]Fig. 7 The morphology of the recovered projectiles after penetration under different velocities[19]

2.4 半流體和流體侵徹理論模型

典型的超高速侵徹過程可以根據彈靶界面壓力隨時間的演化過程劃分為四個階段[74]（見圖8），即階段Ⅰ：瞬態激波階段，階段Ⅱ：穩態侵徹階段（或主要侵徹階段），階段Ⅲ：二次侵徹階段（或慣性流動階段），階段Ⅳ：彈性恢復階段。對于桿形彈而言，階段Ⅱ對侵徹過程起決定性作用，此時可以采用經過修正的穩態流體動力學模型來分析機理；對于球形彈而言，階段Ⅱ的影響很小，一般需要綜合階段Ⅰ和階段Ⅲ進行分析。本節重點綜述桿形彈的超高速侵徹理論模型，球形彈的超高速侵徹理論模型將在本文3.1 節“成坑效應”中闡述。

圖 8 基于界面壓力的超高速侵徹階段劃分[74]Fig. 8 Phases during hypervelocity penetration based on interface pressure[74]

2.4.1 流體動力學模型

桿形彈體超高速侵徹的理論模型最早來自高速射流的流體動力學理論，當彈體的速度極高，彈靶接觸面壓力極大導致可忽略彈體和靶體的強度時，可將桿形彈侵徹簡化為聚能射流問題，彈靶接觸面的壓力平衡關系可由Birkhoff 等[75]建議的伯努利方程描述：

式中： vp為射流速度（彈體尾部速度）， u為彈靶界面速度，ρp為射流（彈體）密度，ρt為靶體密度。假設侵徹為定常過程，可以由公式(13)得到無量綱的侵徹深度：

式中：L 為彈體長度。式（14）被稱為桿形彈的“流體動力學侵徹極限”。需要指出的是，盡管上述計算結果經常被視作連續射流和長桿彈體在速度趨于無窮時的侵徹深度理論極限值，但在現有實驗速度條件下的實際侵深往往與之存在顯著偏差，因此必須對上述模型進行修正以使之更加符合實際。

2.4.2 修正流體動力學模型

侵蝕彈侵徹時，只是彈靶接觸部分呈流體狀態，其余部分還處于剛體狀態[76]，因此實際上不能忽略彈體和靶體的強度特征。流體動力學理論的最大不足在于未考慮材料強度，因而只適用于速度極高情況下的侵徹行為，對于半流體侵徹階段，彈靶相互作用的描述一般采用修正的流體動力學模型。經典的修正流體動力學模型都是首先基于金屬靶體侵徹提出的，包括Allen-Rogers 模型[77]（A-R 模型）、Alekseevskii-Tate 模型[42-44]（A-T 模型）等。

（1）Allen-Rogers 模型

在聚能射流理論的流體動力學模型基礎上，1961 年，Allen 和Rogers 在伯努利方程中加入強度項考慮靶體強度效應的影響，形成Allen-Rogers 模型[77]：

式中： σ于靶體材料強度相關，將該式對時間積分可得無量綱侵徹深度表達式：

當 vp→∞（ 或忽略 σ）時，式(16)可退化成式(14)，Allen 和Rogers 成功用該模型解釋了鎂、鋁、錫等桿形彈高速撞擊鋁靶的試驗數據，在高速侵徹作用下，侵徹深度趨近于流體動力學極限。

（2）Alekseevskii-Tate 模型

A-T 模型是最經典的桿形彈高速侵徹的理論模型，該模型由Alekseevskii[42]和Tate[43-44]各自提出，他們將彈體和靶體材料的強度（Yp和Rt）引入伯努利方程中，并聯合彈長變化方程、侵徹方程和彈體減速運動方程，建立了侵徹計算的流體力學模型：

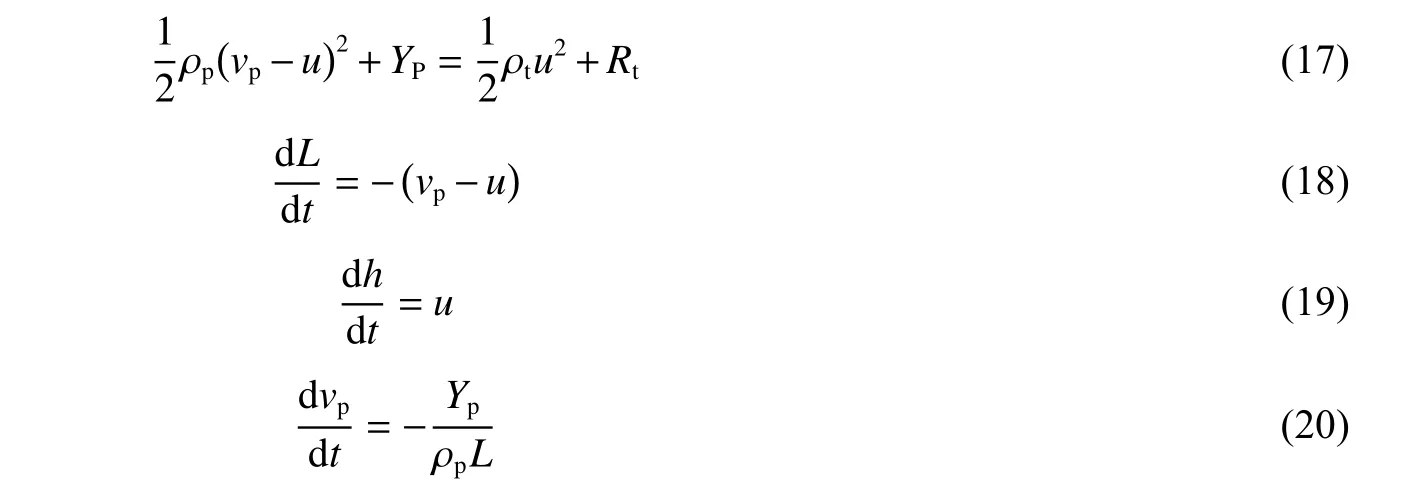
該模型假設彈體侵徹過程中僅彈體頭部較小區域和彈靶接觸面附近靶體處于流體狀態，其余彈體部分仍為剛體。對應不同的彈靶組合，有兩種不同侵徹情形：當Yp＜Rt時，彈體邊侵徹邊侵蝕，直到彈體速度 vp下 降到臨界速度時侵徹停止；當Yp＞Rt時，彈體速度 vp下降到臨界速度，剩余彈體以剛性彈繼續侵徹。

對于A-T 模型求解，一般采用數值方法，由于Yp和Rt會對計算結果有較大影響，因此模型中Yp和Rt取值和理解一直是A-T 模型分析的重點和難點，目前仍難以達成一致性觀點[40]。Tate 最初曾建議將Yp取為Hugoniot 彈性極限（即HEL）[42]，而Rt取靶體材料HEL 的3.5 倍。后來在1986 年，通過實驗數據擬合，重新評估了Yp和Rt[44]：

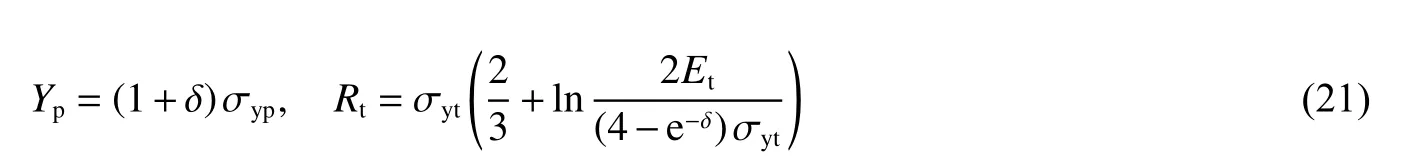
式中：σyp為彈體的動態屈服應力，σyt和Et分別為靶體的動態屈服強度和彈性模量， δ一般取0.7。

（3）其他修正流體動力學模型

在A-T 模型基礎上，國內外學者提出了諸多改進模型，如：孫庚辰-吳錦云-趙國志-史駿模型[78]（S-WZ-S 模型）、Rosenber-Marmor-Mayseless 模型[79]（R-M-M 模型）、Walker-Anderson 模型[80]（A-W 模型）、Zhang-Huang 模型[81]（Z-H 模型）、Lan-Wen 模型[73]（L-W 模型）等。這些模型最早都是針對金屬靶體提出的。樓建鋒[53]對各個模型的基本假設、控制方程和計算結果作了全面的比較，并認為上述模型的關鍵控制方程均可以統一描述為如下形式，即：

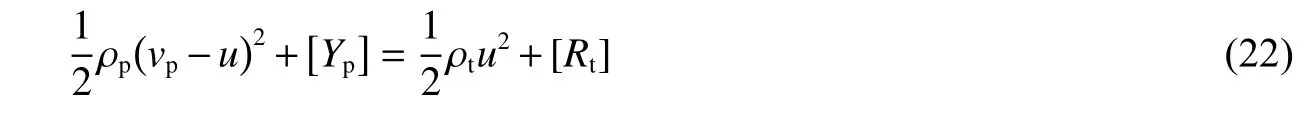
式中： vp和u 分別表示彈體尾部速度和彈-靶界面速度，ρp為彈體密度，[Yp]和[Rt]分別為彈體名義強度和靶體名義阻力。盡管式（22）在形式上實現了模型的統一，但實際上各模型的基本假設、參數取值和預測效果差異很大，在文獻[1]中給出了以上各模型中[Yp]和[Rt]的比較（表2）。

表 2 不同修正流體動力學模型中[Yp]和[Rt]值[1]Table 2 The value of [Yp] and [Rt] in different models[1]

從中可以看出，對于以A-T 模型為代表的修正流體動力學模型，研究的矛盾和難點主要集中在模型中[Yp]和[Rt]的取值。

準確獲知侵徹過程中的[Yp]和[Rt]值是一個十分艱難的任務。對于[Yp]，Rosenberg 等[82]對不同強度長桿彈侵徹的模擬計算表明，[Yp]與彈靶強度、撞擊速度和長徑比都相關，因此認為[Yp]是A-T 模型中不能準確定義的參數。由于[Yp]控制彈體侵蝕和減速，Anderson 等[83]曾建議通過實驗測量彈尾的實時運動來推測[Yp]值，但目前為止，仍未見精確的侵徹過程中[Yp]實測數據。

由修正流體動力學模型的控制方程（公式(22)）可知，影響彈體侵徹效應的是模型中[Rt]與[Yp]的差值[Rt]- [Yp]，目前研究人員普遍認為其對長桿彈高速侵徹能力的影響較小，因此通常取[Yp]為定值或零強度進而主要研究[Rt]的規律。目前常采用三種方式確定[Rt]值[84]：(1) 通過空腔膨脹等理論模型進行推導；（2）通過侵徹實驗數據反向擬合；（3）在數值模擬中獲得瞬時壓力，再對時間或位置積分獲得侵徹中的平均值。由于采用的模型不同，不同的修正理論獲得的[Rt]通常具有顯著的差異[1,84]，由于A-T 及其修正模型主要針對穩態侵徹階段，同時[Rt]在侵徹過程中劇烈變化，因此利用最終侵徹深度反向擬合[Rt]的方法也不盡合理。Anderson 等[83]發現在A-T 模型中，無法同時匹配侵徹速度和侵徹深度，隨后Anderson 等[85]詳細比較了利用侵徹深度反向擬合的靶體阻力和對應數值模擬中按時間平均、按侵深平均及僅考慮穩態侵徹階段的靶體阻力，發現二者差異顯著，在超過4.5 km/s 的撞擊速度下，用侵徹深度反向擬合的[Rt]為負值，這顯然違背了客觀物理規律。在巖石類介質侵徹效應的理論研究，如何準確確定[Rt]和[Yp]值，仍將是一個艱難的工作。

2.5 統一的內摩擦流體彈塑性侵徹理論模型

目前關于侵徹理論計算模型主要分空腔膨脹理論及射流理論兩種，其中空腔膨脹理論主要適用于研究固體彈塑性侵徹問題；而射流理論則主要適用于研究流體動力學侵徹問題，目前尚缺乏一種涵蓋從低速至高速、超高速侵徹的全過程理論模型。王明洋等[31-32]、李杰等[86-87]在系統總結爆炸和沖擊加載作用下巖石動態壓縮試驗數據的基礎上，指出：在固體彈塑性侵徹區域與流體動力學侵徹區域之間，還存在一個擬流體過渡區，在這一區域材料的行為兼具固體和流體屬性，隨后創新提出流體彈塑性內摩擦侵徹理論，表征了材料從低應力固體彈塑性至高應力流體之間的應力狀態，推導出了從固體侵徹至流體侵徹全過程的阻抗演變公式：

式中： v?和 v??分別為巖石介質進入擬流體侵徹和流體動力學侵徹對應的彈體臨界速度，按公式(5)～(6)確定，dv為擬合系數，由試驗確定，隨彈速增加，公式（24）中不同項應力影響分配份額發生變化，根據侵徹壓力狀態遞進過程中，不同參數演化趨向極限的程度，將侵徹過程分為固體侵徹、半流體侵徹和流體動力學侵徹。下式給出了3種侵徹情況下，阻抗的計算公式和速度閾值：

在不同的侵徹狀態下，通過對彈頭進行受力分析得到彈體的最終侵徹深度。

2.5.1 剛性彈侵徹階段

在剛性彈侵徹時，巖石介質處于固體侵徹狀態，根據牛頓第二定律得到彈體運動微分方程[32,51,66]：

式中：F 為彈頭阻力，受彈頭形狀影響，應通過分析心角為θ0（ θ0=arctan((s?r0)/s)=arctan(1?1/2ψ)，ψ=s/2r0為彈頭頭部曲率），彈體垂直侵入靶體，初始侵入速度為 v0，中途侵入速度為 vp，則作用在彈彈頭微面積上的阻力積分得到。例如，對于弧形彈頭（見圖9），設彈桿半徑為r0，彈頭表面某點的法線方向與彈軸的夾角為θ，彈頭圓弧半徑為s，圓體頭部微面積上的法向阻力和切向阻力分別為：

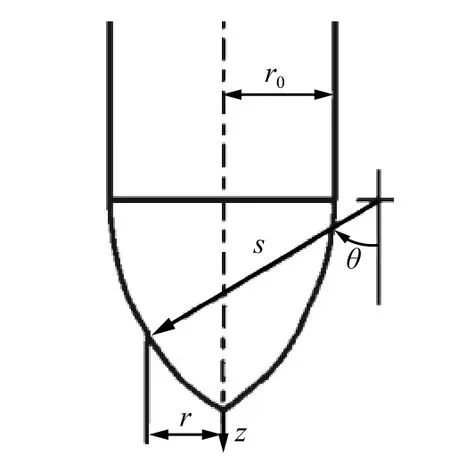
圖 9 弧形彈頭的幾何參數Fig. 9 Ogive-nose projectile geometry

式中： σr按公式(25)固體侵徹階段取值， μs為彈靶間摩擦因數，則彈頭軸向合力為：

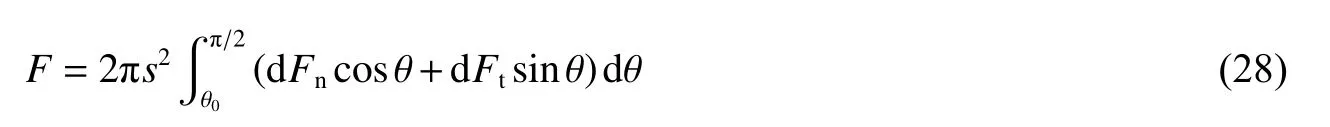
王明洋等[51,66]分析了不同彈體形狀下剛性彈侵徹階段彈體侵徹深度，統一用下列公式表示：

對于弧形彈：

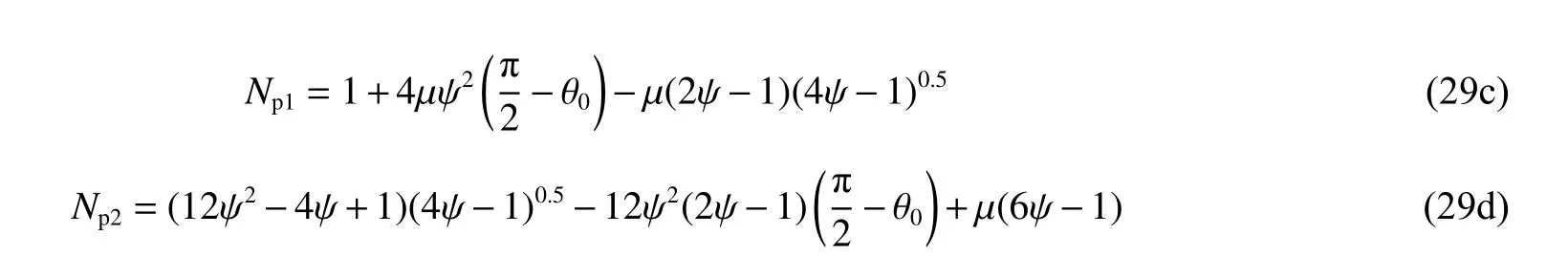
當0.1≤v0/cp≤0.2時，式(29a)中對數項影響小于5%，可簡化為：

2.5.2 侵蝕彈侵徹階段

隨著侵徹速度進一步增加，當巖體介質阻抗超過彈體的動力屈服強度時，彈頭將發生屈服、磨蝕，造成由于彈體變形和質量損失帶來的侵徹深度的急劇下降，仍然采用式（26）所示的控制方程，但需要引入彈體質量的損失與侵徹速度的關系[32]：

式中： mp0為彈體的初始質量， vcr為發生質量損失的臨界速度，由條件σr=Yp來確定，當 vp＞vcr時，彈體侵徹時出現質量侵蝕，侵徹過程中，彈體速度不斷減小，被侵蝕的質量不斷增加，當速度降低至 vp≤vcr時，彈體重新恢復剛體侵徹，彈體質量不再發生變化，αe為質量損失參數，可通過實驗確定。

此時將公式（31）代入彈體運動微分方程（26），可得到侵蝕彈侵徹階段彈體侵徹深度計算公式：

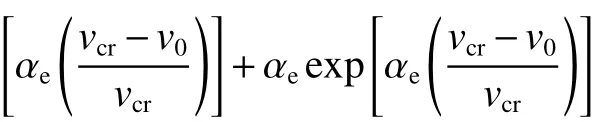
2.5.3 內摩擦擬流體侵徹階段

對于堅硬巖石，當靶體進入內摩擦擬流體狀態時，彈體一般也已進入流體狀態，此時須采用修正的流體動力學方程描述彈體行為，即[32]：

式中： σr按公式(25)擬流體侵徹階段取值。若彈體強度Yp可忽略，在理想定常侵徹條件下，得到侵徹深度計算公式：

式中： κ按公式(24)函數給出。對于非定常侵徹，可取公式(33)為控制方程，并聯合A-T 模型的彈長變化方程、侵徹方程和彈體減速運動方程進行數值求解計算。

2.5.4 流體動力學侵徹階段

在公式(34)中，若κ→1，進入流體動力學階段，侵徹深度計算公式演化為[32]：

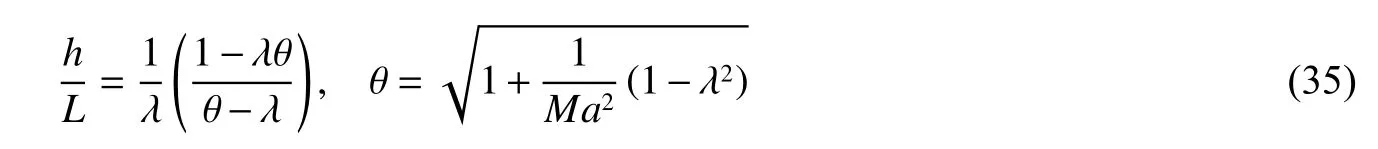
隨著 Ma的 增大， θ →1，于是式(35)退化成為：

內摩擦侵徹理論模型實現了由低速至高速、超高速侵徹的全過程計算，并得到了1.0～5.0 km/s鋼彈侵徹花崗巖的試驗驗證[32]（見圖10）。

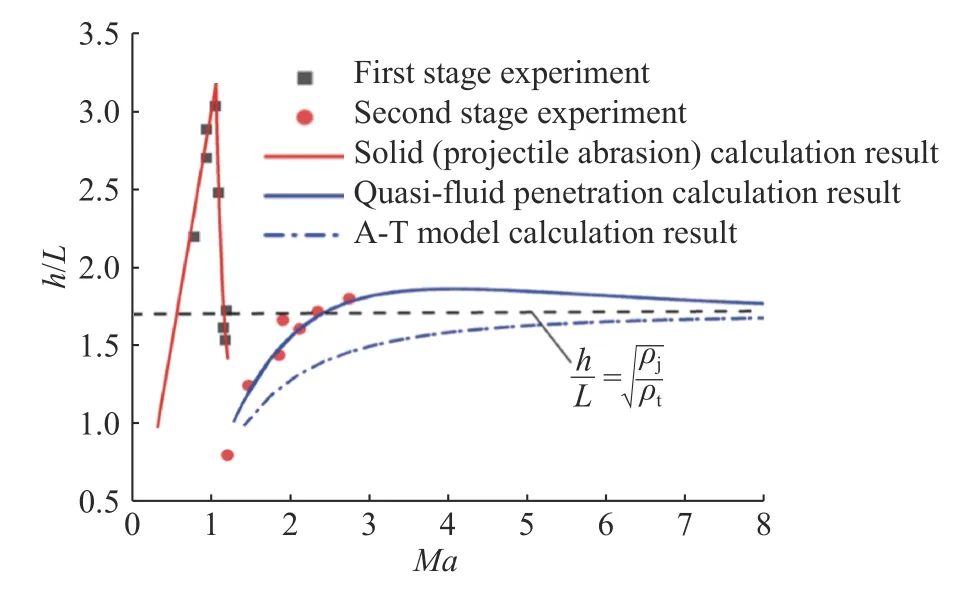
圖 10 花崗巖侵徹深度的實驗結果與理論計算結果的預測效果[32]Fig. 10 Comparison of calculation results with experimental results of penetration depth in granite[32]

3 超高速侵徹成坑和地沖擊效應

研究表明，隨著彈體速度提高，超高速侵徹深度逐漸趨向極限，但彈體動能急劇釋放引起的極端高溫高壓過程致使彈坑半徑呈現非線性擴增現象，同時產生類似于爆炸的強地沖擊現象，其本質是一種幅值高、作用時間長的應力波[13,33]。由成坑效應和地沖擊效應帶來的附加毀傷效應值得引起工程防護設計和武器研發人員的重視，同時對研究隕石撞擊效應和破巖技術具有重要的意義。

3.1 成坑效應

目前成坑效應的研究主要集中于球形彈撞擊效應，研究背景主要來源于破片或太空垃圾對航天航空飛行器的破壞以及隕石對類地星體的撞擊成坑等。對于地質類材料，地質學和行星學家圍繞小行星和隕石撞擊成坑效應，開展了大量室內模型實驗，并綜合采用參數擬合方法以及半解析手段得到了金屬介質中的成坑尺寸計算公式。如Burchell 等[88]根據花崗巖的撞擊試驗擬合獲得了經驗公式：

式（37）要求采用mm、km/s 作為長度和速度單位；Takagi 等[89]根據玄武巖的撞擊試驗得到了成坑參數和彈體動能之間的關系

更早時候，Donald[90-91]基于100 多次玄武巖和花崗巖的試驗結果歸納出了成坑深度和成坑直徑的經驗公式

式（39）要求采用cm、g、s 作為長度、質量和時間單位進行計算，其中i 是入射角度，以垂直入射為i = 90°且要求i＞15°。

以上關系大多是零星的經驗公式，缺乏針對不同因素、不同尺度下相似關系的考慮。經典的超高速撞擊成坑的相似關系在Kinslow[92]和張慶明等[93]的著作中得到了較為充分的總結，而專門針對地質類材料的相似關系的系統理論成果則首推Holsapple、Housen 和Schmidt 等學者等在過去二十多年積累的成果[94-101]，其形式總體滿足表2 的結果，其中ρp為彈體密度，a0為彈體半徑，Yt為靶體強度，ε 為靶體孔隙率參數，含有不同下標的f 為ε 的函數且與對應的幾何參數和控制區域有關，g 為重力加速度，ξ1，ξ2為擬合常數。其中ξ2一般取為1/3，1/3＜ξ1＜2/3 且ξ1與ε 有關：當ε = 30%～35%時，ξ1=0.4；當介質孔隙率較小時，ξ1=0.6。當彈體直徑不超過～10 m 級別時，成坑相似率在強度控制區域；而當彈體直徑超過～10 m 級別時，成坑相似率在重力控制區域。表3 中的公式得到了海量實驗數據的驗證并形成了適用于寬廣條件的計算參數，因此得到了較為廣泛的應用并有專門的網站供讀者進行估算[102]。近年來MEMIN 課題組利用上述相似關系開展了大量的室內模型實驗[103-108]，并從宏觀和微觀角度加深了對成坑機理的理解。

表 3 地質類材料成坑效應的相似關系Table 3 Similarity laws of cratering effects in geological material

目前對于桿形彈成坑效應的研究不多。但目前隨著高超聲速動能武器的發展，已逐漸引起世界各國學者的關注。

完整的成坑效應包括不同侵徹深度處彈坑橫向尺寸的全部信息，一般來說，地質材料和金屬介質的撞擊成坑外觀差異十分顯著（見圖11）。在垂直撞擊下，金屬介質中將形成內壁光滑、輪廓清晰的圓形截面彈坑（圖12(c)），在彈坑邊緣可以觀察到顯著外翻的“唇沿”，附近介質顯著隆起[93,109]。相比之下，巖石介質中的成坑一般難以用簡單形狀函數描述，其典型特征是在中央坑周圍存在一個邊緣極不規則的剝裂區域，其內壁凹凸不平。這一不規則區域主要是由于反射應力波引起的表面剝離效應，一般認為是與巖石介質抗拉強度低、脆性顯著、內部缺陷分布有關。

圖 11 巖石與金屬靶體超高速撞擊成坑的典型外觀[106, 109]Fig. 11 Typical appearance of craters formed by hypervelocity impact[106, 109]

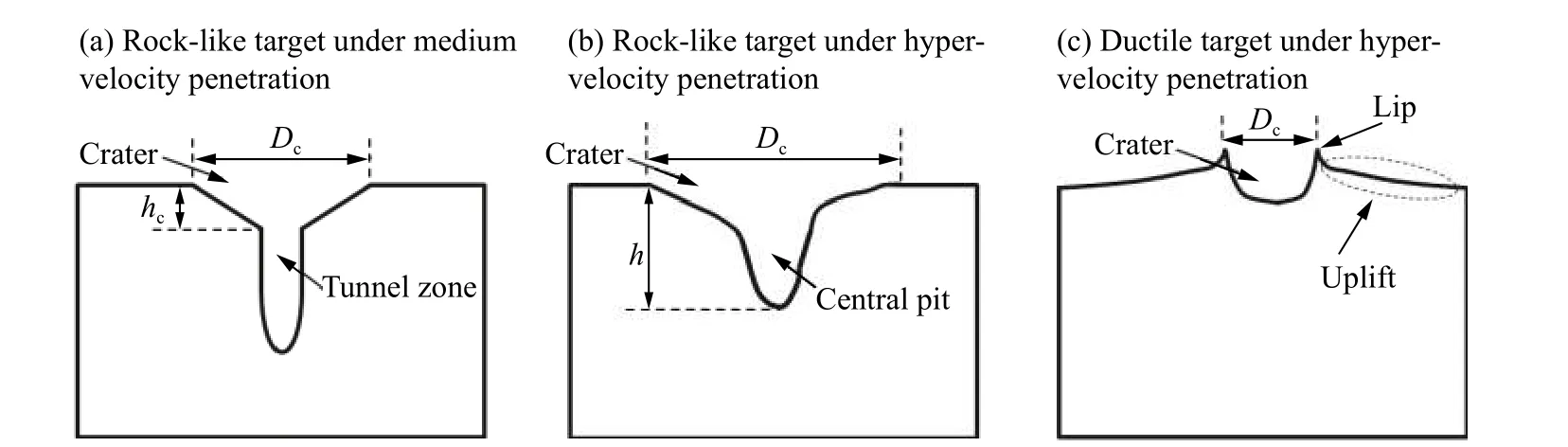
圖 12 不同條件下的成坑效應Fig. 12 Cratering effects under different conditions

當撞擊速度較低時，典型巖石介質成坑效應包括表面淺碟形的開坑區和隧道區（圖12（a））[110-111]；當撞擊速度較高時，上述兩個區域的邊界趨于模糊，隧道區逐漸演化為中央彈坑（圖12（b））[19, 21-22, 103-108, 112]。

現有研究主要針對開坑區范圍計算。Forrestal 等[23、Frew 等[113]對一般彈道速度下開坑區深度hc和開坑直徑Dc進行了分析，認為混凝土hc是彈體直徑的2 倍，Dc為彈體直徑的2～8 倍。Li 等[111]采用滑移線理論給出了混凝土hc的深度的簡化計算方法，并認為其主要取決于彈頭形狀和彈體直徑，與撞擊速度無關。劉海鵬等[110]給出了混凝土hc和Dc的解析計算方法，發現開坑區傾斜角度與材料的力學性能和撞擊條件關系不大并接近于24.7°。

由于長桿彈成坑效應機理復雜，對于長桿彈成坑效應的計算主要采用半理論半經驗的計算公式，許多學者將類似于表2 中的相似關系引入長桿彈侵徹，并通過試驗建立了成坑效應計算公式，如錢秉文等[21]利用Holsapple-Housen 模型得到了鎢合金短桿彈超高速侵徹混凝土成坑效應中Dc和Vc的歸一化表達式：

式中：k 為擬合參數，Yt取混凝土單軸抗壓強度。程怡豪等[114]得到了涵蓋文獻[21-22,29]實驗數據的混凝土成坑深度的分段計算公式（見圖13）：

式中：Yt建議取為式（8b）中的Rt。

以上半理論半經驗公式具有簡單直接的特點，在實驗特定的范圍之內具有較高的準確性，其缺點在于介質的特征參量和彈體的侵徹速度、幾何尺度等一旦超出實驗范圍，就會很容易造成預測預報的偏差，因此需要從巖石的成坑機理出發，建立物理意義明確的理論模型。

圖 13 式（41）與混凝土超高速侵徹深度實驗結果的對比[114]Fig. 13 Comparison between Eq. (41) and experimental results of hyper-velocity penetration depth into concrete[114]

圖 14 高速彈體侵徹巖石擴孔范圍計算簡圖[116]Fig. 14 Calculation diagram of cavitation induced by high-velocity projectile penetration into rocks[116]

目前對于長桿彈成坑效應的理論模型，較為經典的是Slepyan 模型。桿形彈超高速撞擊巖石過程中，彈靶近區巖石的超高壓力致使巖石破碎，并經由彈靶接觸邊界向外噴射[21,115]。Slepyan[116]采用如圖14所示的計算模型研究了擴孔范圍，圖中Ω1（實質上是一個外直徑2R0的變截面空心圓柱）為擬流體區，該區域的破碎巖石可以視為無黏性不可壓縮理想流體；Ω2為裂紋區，該區域內的質點位移很小并可視為剛性；Ω3為彈性區，仍舊保持著巖石的初始物理力學特征。擬流體區與裂紋區的邊界滿足P=Ht，并且隨著彈體的侵徹，該邊界不斷沿著x1軸移動。因此，上述問題轉化為擬流體破碎介質以強度為邊界的管道中遇到彈體阻礙時的流動問題。

Slepyan 模型將破碎巖石可以視為無黏性不可壓縮理想流體，實際上由于巖石力學性質特殊性，很難達到如此力學狀態。王明洋等[31]在Slepyan 模型基礎上，通過內摩擦理論（2.5 節）對模型中流體項的修正，得到Ω1內的伯努利方程和連續方程為：

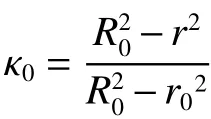
Ma=vp/c?0， 的計算可借助Gurevich[117]的研究結果：對于彈體侵徹這類圓錐體的軸對稱問題求解極其復雜，但是試驗與數值分析表明，平面問題與軸對稱問題的壓縮射流系數基本相等，可以將等效楔形體所致的壓縮射流系數視為相應圓錐體的壓縮射流系數。平面問題壓縮射流的系數由下列公式確定：

式中：α 是楔塊頂端的半角（0 ＜α≤π/2） ， x=α/π， ζx=Ma·(1+Ma2)?0.5。

通過粉碎區邊界壓力做功與裂紋增長能量之間的關系，得到徑向裂紋區半徑 Rc簡單的相似關系：

圖15 給出了擬流體侵徹范圍徑向裂紋區半徑理論計算結果與花崗巖中實驗結果對比。結果表明，相較于Slepyan 模型，利用內摩擦理論修正的計算模型撞擊成坑計算公式與實驗結果吻合更好。

以上公式及表2 的結果均是針對超高速撞擊成坑最終形態的計算公式，不能再現成坑的全過程。Maxwell 的Z 模型[118]是較早成功用于描述超高速撞擊成坑和核爆成坑過程的理論模型，該模型對彈坑邊緣和前驅沖擊波陣面之間的速度場進行矢量化描述，并在一定的邊界條件和初始條件下求解最終成坑尺寸和介質拋射過程，其基本控制方程為：

圖 15 徑向裂紋區半徑計算結果與實驗結果對比[32]Fig. 15 Comparison of crater radius between calculation results and experimental results[32]

式中： R為 徑向方向向量，αz和Z 近似為常數， U為速度場向量。式（46）描述了沖擊波后不可壓縮條件下流場的運動，當Z = 2，3，4 時，沖擊波后流場如圖16 所示。求解Z 模型尚需材料本構模型和邊界條件，過程較為復雜，一般必須借助于數值方法，但對于特殊情形可以求得解析解。例如文獻[34]的模型可以視作Z=2 時的特例，此時流場滿足球對稱條件，因此可以采用球形空腔膨脹理論進行分析。

圖 16 Z 模型在不同Z 值下的速度場[118]Fig. 16 Streamlines with different values of Z[118]

綜上，超高速打擊情況下，彈靶界面處的沖擊壓力遠大于材料的動態強度，材料呈現出準流體或流體狀態，在接觸面周圍流動，最終形成遠大于彈體口徑的彈坑，并在彈坑周圍形成破碎區和徑向裂紋區，巖石的成坑特性反映了彈體打擊過程中能量分配的份額，從而決定了輻射出來的應力波基本參數，對于評判超高速動能武器打擊的毀傷效應具有重要價值，但是相關研究尚不完善。目前在實驗上僅能獲得打擊結束后靶體的成坑形貌，很難連續測得彈坑的形成規律，因此難以建立起能精確描述成坑效應的理論模型，而且對影響成坑的主要因素尚存在分歧。目前迫切需要對超高速侵徹過程中彈靶接觸面的介質壓碎過程、塑性流動軌跡、應力波反射剝離效應等進行更加詳細的理論分析、試驗量測和模擬研究工作，從而建立起更加具有物理意義的力學模型。

3.2 地沖擊演化規律

爆炸與撞擊都是能量的高速釋放轉化過程，屬于高壓力、高應變率、高溫度的作用過程，鄧國強等[13,119]對超高速武器對地打擊效應進行了數值仿真，結果表明超高速對地打擊將形成塑性沖擊波，在彈坑形狀、沖擊波波形及衰減規律上高能裝藥的淺埋爆炸效應均具有一定相似性，所不同的是超高速撞擊過程中彈體動能具有定向性。

Oberbeck[120]通過實驗表明：在動能一定的情況下，可以用爆炸能量等于彈體動能、且爆炸沖擊波壓力峰值等于超高速撞擊沖擊波峰值的淺埋爆炸來模擬超高速撞擊，實驗利用長4.6 mm、直徑6.4 mm、質量0.435 g 的圓柱形鋁質彈丸，以2.00 km/s 的速度撞擊石英砂靶體，彈體的動能為870 J，彈丸對石英砂的沖擊壓力峰值為8 300 MPa。使用和彈丸形狀一模一樣、裝填密度為1 g/cm3的0.15 g TNT 炸藥（爆炸沖擊波壓力峰值為8 300 MPa），進行淺埋爆炸，裝藥中心埋深分別為0、3.2、6.3、9.5、14.3 mm。對比發現，炸藥埋深為6.3 mm 左右（比例埋深）時，爆炸彈坑和撞擊彈坑匹配最好。

Baldwin[121]認為，對于特定的彈靶組合和炸藥，等效模擬存在速度限制。以鋁質彈丸高速撞擊石英砂為例，如果彈丸撞擊速度高達9.6 km/s，則彈丸在石英砂中產生的沖擊波壓力高達50 GPa，而裝填密度為1.6 g/cm3的TNT 炸藥爆炸沖擊波壓力峰值為23 GPa，同時要求二者的單位能量和沖擊波壓力峰值都相等有很大困難，用爆炸模擬將不再合適。

Holsapple[122]以彈坑體積相同為標準，提出了化學爆炸模擬超高速撞擊問題中“等效埋深”的概念，多種撞擊條件和化學爆炸條件下，石英砂中的等效埋深實驗結果，并通過試驗得出了定性結論：撞擊速度固定的情況下，隨著撞擊能量的增加，等效埋深減小；撞擊能量固定的條件下，隨著撞擊速度的增加，等效埋深減小。

王明洋等[32-33]認為，從力學本質上講，巖石中超高速撞擊與淺埋爆炸都屬于強動載作用下材料動力學行為和過程的問題，二者近源區產生強沖擊波，隨著傳播距離增加迅速衰減為短波、彈塑性波，波的傳播衰減規律相同，可以用相同的物理力學方程描述。隨后王明洋等以彈坑體積和形態為等效指標（基于沖擊成坑深度確定等效裝藥埋深，基于沖擊成坑半徑確定彈坑拋擲指數），建立超高速撞擊與標準裝藥爆炸的能量等效關系：

式中： kδ為爆破多方指數，與炸藥和巖石性質有關； Nδ=R/h 為彈坑形狀系數； R為表面成坑半徑。

與化爆、核爆一樣，超高速撞擊引起的地沖擊也可在一定范圍內采用以下公式描述[32,123]：

式中：σpk為應力波峰值，r 為撞擊點到考察點的距離，n 為衰減指數。衰減系數 n的取值與巖石壓力狀態密切相關。Melosh[123]較為系統地闡述了地質材料的超高速撞擊成坑及沖擊波傳播的過程，如圖1 所示，在速度10 km/s 的彈體的撞擊下，彈體和巖石靶體之間形成峰值壓力50 GPa 以上的沖擊波并向地下傳播，波的傳播規律如圖17 所示，在50 GPa 以上的強沖擊區波的壓力衰減指數約為3.6，在5～20 GPa 的過渡壓力范圍內衰減指數約為1.4～1.8，在小變形彈塑性變形區衰減指數約為1.1～1.2（見圖18）。

哈努卡耶夫[124]總結了值與側壓力系數α 間的簡單關系：

式中：正號對應沖擊波傳播區域（高應力流體狀態），負號對應固體彈塑性波傳播區域（低應力固體區）。在高應力流體區， α ≈1， 故 n ≈3 ，在低應力固體區， α ≈0.2～0.6，上述關系大致描述了n 值從近區（n＞2）向遠區（n＜2）突躍式減小的現象。

借助于室內縮比撞擊試驗與預埋壓力傳感器的方法可以直接測得不同位置的壓力變化，進而得到壓力隨距離衰減的真實過程。程怡豪[125]總結了不同文獻中實測或數值計算得到的衰減指數（見表4）。

對于巖土中爆炸應力波波形計算，應用最多的是文獻[126]提供的計算公式：

式中： α=1/ta, ta=r/ct為達到時間，tr為升壓時間，f 耦合系數，ρt為靶體材料密度，cP縱波速度，Q 為等效TNT 當量；r 為爆心至測點距離， n為衰減指數。

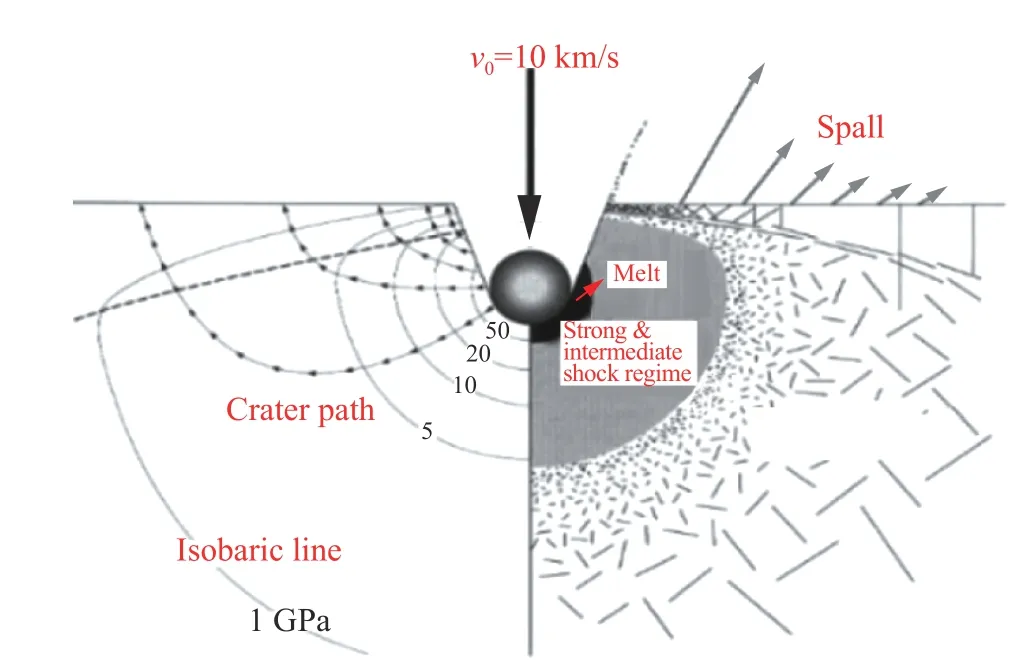
圖 17 球形彈超高速撞擊下介質中壓力分布[123]Fig. 17 Pressure distribution in medium under hypervelocity spherical projectile[123]

圖 18 峰值壓力隨距離衰減曲線[123]Fig. 18 Peak pressure decay with impact of distance[123]

表 4 地質類材料地沖擊衰減指數nTable 4 Power exponent n for attenuation of ground shock in geological material

花崗巖中超高速撞擊地沖擊試驗證實，按公式(50)計算的應力波形與實測波形基本一致（見圖19～20）。

綜上，在超高速彈體對地撞擊時，產生類似于淺埋裝藥爆炸的強地沖擊效應，在進行防護工程抗超高速動能彈打擊最小安全防護層厚度設計時，除侵徹近區的局部破壞效應（侵徹、成坑）外，還應考慮由于超高速撞擊所引起的地沖擊荷載。近年來，在超高速動能武器研制及工程防護需求的推動下，不同學者對下地沖擊演化及壓力峰值衰減規律進行了研究，建立了超高速撞擊巖石地沖擊效應與淺埋爆炸的等效計算方法，但相關研究還未達到機理明晰的地步：（1）對于衰減系數n，目前仍主要采用基于試驗擬合和數值模擬所得到的經驗系數，還未建立系數n 與應力波、巖石力學參數的關聯關系；（2）由圖18 和公式（49）可知，參數n 隨距撞擊源（或爆心）比例距離的增加而急劇減小，這也造成衰減系數n 擬合的主觀性，在試驗過程中測點位置、測點數目的變化均可造成n 值的較大差異；（3）目前超高速彈體侵徹巖石的地沖擊效應試驗主要采用室內縮比撞擊試驗與預埋壓力傳感器的方法，由于巖石尺度小、地沖擊衰減快造成了試驗測量的困難，同時在巖石中預埋壓力傳感器的方法破壞了巖石的整體性，也會對試驗結果造成誤差，如何實現超高速撞擊過程中地沖擊傳播的高分變率全過程觀測仍是未來發展的方向；（4）超高速侵徹地沖擊效應的數值模擬研究發現[13,119]，超高速成坑地沖擊具有定向傳播特性，同時由于彈靶界面移動速度接近應力波傳播速度，其追趕前驅應力波會產生壓力波形的疊加倍增效應，相關現象采用等效計算的方法難以準確描述，需要建立更加準確的計算模型。

圖 19 彈速3 558 m/s 時實測地沖擊壓力時程曲線[32]Fig. 19 The experiment time history curve of ground shock with impact velocity 3 558 m/s[32]

圖 20 彈速3 558 m/s 時按公式（50）計算的地沖擊壓力時程曲線[32]Fig. 20 the calculated time history curve of ground shock with impact velocity 3 558 m/s[32]

4 結論與展望

超高速武器是當今軍事強國致力發展的下一代武器系統，近年來，國內外學者圍繞超高速動能武器打擊巖石的毀傷效應與工程防護問題進行了廣泛而細致的研究，取得了豐富的研究成果。本文中圍繞大速度范圍內巖石介質的侵徹效應經驗公式、侵徹理論模型、成坑效應和地沖擊效應的研究成果進行綜述，通過對相關文獻的查閱分析，得到的主要結論和建議如下：

（1）大速度范圍內桿形彈的侵徹效應具有明顯的多階段特征。隨著撞擊速度增加，彈體將經歷從變形可忽略的階段（僅有少量質量損失）向侵蝕階段（即彈體長度嚴重縮短）的轉變，靶體材料經歷從固體侵徹、內摩擦擬流體侵徹項動力學侵徹行為的轉變，侵徹深度經歷“迅速增加—逆減—緩慢增加—趨于流體動力學極限”的過程，不同階段的物理機理不同，在進行侵徹效應計算時需要考慮所采用的物理力學模型對不同彈靶狀態的適用性問題。

（2）近年來圍繞巖石和混凝土介質的侵徹深度計算問題開展了大量研究，建立了空腔膨脹、修正流體動力學、內摩擦流體彈塑性等理論模型，實現了對大速度范圍內侵徹深度變化規律的描述。但相關研究仍或多或少存在表征不夠精細的問題，一些參數的獲取仍然具有明顯的經驗性，甚至存在一定爭議，需要更進一步的深入寬廣應變率范圍內巖石的動態力學行為，盡可能的了解不同加載范圍材料的實際性能。

（3）超高速侵徹過程下的成坑和地沖擊效應不可忽視，但目前相關理論研究仍處于起步階段，主要采用半理論半經驗的計算公式，需要從超高速侵徹成坑、地沖擊演化的三維效應和力學機制出發，構建更加完善、更加細致的演化模型。

（4）由于巖石的工程地質屬性，其變形破壞具有顯著的尺度效應，由于發射手段限制，目前超高速侵徹效應理論的研究缺乏大尺寸彈體的超高速侵徹實驗驗證，需要發展更為先進的試驗設備和技術，針對不同彈靶材料開展大尺度、速度范圍的室內相似模擬與原型試驗，建立寬廣尺度范圍內彈體侵徹的相似規律。