淺談高中數學解題中轉化思想的應用
趙思麒
重慶市第十一中學校 重慶 400000
高中數學作為一項極具抽象性及邏輯性的理科課程,高中生在解答相關習題時應充分掌握解題技巧、結合多種解題思路、靈活轉變思考方向,這就對轉化思想的運用提出了極高的要求。為了更好的應用轉化思想,以提高高中生的解題效率,本文從轉化思想的含義與其在數學的解題應用方面進行了詳細的分析。
1 轉化思想的實質
轉化思想的實質在于將復雜問題轉變為簡單直觀的問題,不僅可以便于高中生理解問題,同時也可以提高做題效率。高中數學由于其知識點繁雜,體系龐大,造成高中生在解題過程中需要對不同知識的關聯性有深刻的理解,才能解決相關數學題目。因此,高中生首先應逐步對問題進行細致分析,并掌握等價轉化的解題思路,繼而充分運用所學知識準確地解決問題。通過轉化思想將問題化繁為簡,大大降低了高中生的解題難度從而縮短了解題時間[1]。
高中生在應用轉化思想進行解題時,應注重思考角度的轉換,不僅要從多角度看待問題,而且應看到問題的正反面。當遇到難度較高的問題時,高中生能夠學會以反面的角度來對問題進行思考及探索,這不僅擴寬高中生的解題思路,而且對培養高中生逆向思維起到了良好的促進作用。
2 轉化思想在三角函數問題中的應用
在高中數學考試中,三角函數是常考題型,由于三角函數知識點和公式繁多,且其分值比較高,所以高中生應重視三角函數題型。在三角函數題型中,高中生遇到的角度都不是特殊角,如果單純直接計算,就需要查表,然而在考試中顯然是不可行的。因此,高中生應運用轉化思想,將三角函數中的特殊角與題目中的角度建立聯系,這樣三角函數問題就能迎刃而解[2]。
3 轉化思想在概率問題中的應用
概率問題是高中數學中最容易丟失的部分。許多學生認為用兩個參數求解概率問題時,分析過程相當復雜,解決思路比較混亂,針對具體問題難以解決。如果學生使用轉換的思想,他們可以簡化概率問題。例如,使用該列表可以使兩個參數的值一一出現,使學生的思想更加清晰明了,從而快速解決概率問題[3]。
例.有5張白卡、5張黃卡和5張紅卡,分別是數字1、2、3、4和5。每次考試都要抽一張牌,用i表示1、2、3、4、5。并做出如下規定:抽取的是白色的卡片,則得分;如抽取的是黃色的卡片,則得+1分;抽取的是紅色的卡片,則得i+2分。
(Ⅰ)求得分為3分的概率;
(Ⅱ)求得分大于3分的概率。
解:將白色卡片用k=0表示、黃色卡片用k=1表示、紅色卡片用k=2表示,則每次試驗抽取一張數字為i的白色卡片、黃色卡片、紅色卡片分別所得分為(+0)分、(+1)分、(+2)分,所有得分情況如下圖:
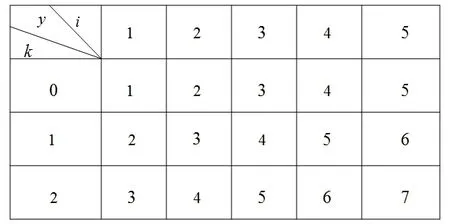
由上圖可知試驗的基本事件總數為n=15,得分y取的值分別是1,2,3,4,5,6,7對應的基本事件個數分別為1,2,3,3,3,2,1。
(Ⅱ)得分大于3分包含的基本事件的個數為3+3+2+1=9,即得分大于3分的概率為
4 結語
從高中數學習題解析過程中可見,其習題類型更多的是由固有的知識點來進行變形和延伸發展而形成的。而在高中數學習題中運用轉化思想,可以激發學生的發散性思維,同時也能夠在鞏固原有知識的基礎上,進一步地探究數學知識應用路徑。所以,轉化思想不僅可以幫助學生解題,更重要的是它還可以開拓學生的思維,讓學生達到學習的真正目的。

