基于動態特性的數控銑削參數自適應在線優化

劉恒麗，王 勇，董靖川

LIU Heng-li1，WANG Yong1，DONG Jing-chuan2

（1.天津商業大學，天津 300134；2.天津大學 機械工程學院，天津 300072）

0 引言

在數控加工過程中，切削力控制問題一直是制造業研究的永恒話題[1]，并且近年來，大都是基于自適應控制技術，通過傳感器在線監測被控量，采用智能算法和控制策略對切削參數進行在線調整和優化，從而實現切削力穩定控制[2～7]。

智能算法中，模糊邏輯算法最為常用，由于其控制規則決定著自適應控制器的性能，因此，近年來關于控制規則的產生和優化成為國內外學者研究熱點，并且同時也代表了數控加工參數在線自適應優化技術的發展程度。最常用的大都是基于經驗和知識庫而建立的控制規則，比如，文獻[8]基于脈沖分析和經驗建立模糊控制規則，對電火花切削加工中的切削力和功耗進行自適應控制。文獻[9]采用傳統的模糊控制方法，通過調整進給速度，控制主軸負載力，實現加工過程在線優化。文獻[10]采用基于動態閾值的模糊自適應控制策略，對影響磨削力的磨削深度和擺動角速度在線模糊調整，以適應磨削過程并保持磨削過程穩定，但模糊控制算法也是使用基于知識庫和經驗數據的語言規則完成控制動作。

隨著對加工質量要求的提高，為了提高控制器性能，專家學者們開始對模糊控制規則進行優化研究，采用智能算法對控制規則進行優化，如：基因遺傳算法[11]，神經網絡算法[12]等。而文獻[13]將灰色預測理論與傳統的模糊控制器相結合，避開了研究非線性復雜系統的動態性能及控制規則和隸屬度函數的建立和選擇，但是預測參數變化趨勢，并非真實趨勢，準確性較低。文獻[14]采用基于RBF神經網絡與自組織混合模糊控制器，保證車削過程穩定；通過徑向基神經網絡使得自組織模糊控制器的學習率和權重分布調節到準確值，避開了模糊控制規則的建立問題，但基于神經網絡擬合得到的輸入輸出關系不能反映真實情況，并且所基于的樣本數據有限，使得擬合關系可靠性較低。文獻[15]用公式即加權系數來調整控制規則，具有一定的主觀性。文獻[16]提出通過學習能自動產生模糊規則的神經模糊網絡系統，但還停留在理論階段。

通過以上研究可以得出，基于模糊邏輯算法的切削力自適應控制得到廣泛應用，但決定控制效果的控制規則庫大多基于專家知識和經驗而建立，或是基于各種算法優化，甚至直接回避控制規則的建立問題，均不考慮或簡化系統動態特性，有一定的局限性，從而影響控制效果和加工穩定性。基于此，本文提出了一種基于數控加工系統動態特性的模糊自適應控制策略，克服了模糊控制規則庫基于經驗和預測方法建立的缺陷，使數控切削過程更加穩定。

1 銑削過程分析

數控銑床是一個典型機電系統，包含執行部件、傳動系統、伺服驅動系統等，如圖1所示。在銑削加工過程中，負荷的產生和傳遞的過程如下：

1）切削力的產生：刀具主切削運動和工件進給運動形成一對相互作用力，使刀具—工件產生變形，完成切削。

2）切削負荷的傳遞：切削負荷產生于主軸末端，以轉矩的形式體現，經過中間的齒輪減速器或齒形帶向后傳遞給負載轉矩。

3）機電轉換過程：電機輸出電磁轉矩與電機軸摩擦轉矩，再加上切削轉矩、主軸慣性轉矩，這幾個轉矩之間的平衡在主軸上實現。

可見，機電系統兩端的參數是主軸電流和切削負荷，并且兩者之間存在著一定的關聯。

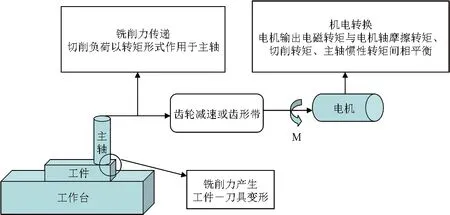
圖1 銑削過程分析

2 數控加工切削力自適應控制系統模型

2.1 切削力與電流關系

通過銑削加工過程分析，得到了主軸電流和切削負荷之間存在一定的關聯。近年來國內外學者的一些研究文獻也表明了電機電流與切削力間的關系，并通過測量電機電流來間接監測切削力。文獻[17]對于切削力與電流之間關系進行研究，從理論和實驗角度證明了主軸電機電流特征值的變化可以很好地反映出切削力的變化。文獻[18]采用小波分析理論對主軸電流信號進行處理，主軸電機電流信號幅值的變化會因刀具負載轉矩的變化而改變。文獻[19]從理論和實驗角度證明了主軸電機電流特征值的變化可以很好地反映出切削力的變化，通過測量主軸電機電流來間接測量切削力是合理可行的。文獻[20]對機床進給控制系統進行了詳細的分析，并利用電機電樞電流信號得到力信號。文獻[21]立足于進給系統的動態模型，針對直流進給伺服電機中的電流信號和力信號間的關聯性進行研究。文獻[22]所進行的研究工作立足于神經網絡法，創建了有關主軸電機電流和切削力的關聯性的模型，進而對就切削力實施估算。

2.2 數控加工自適應控制系統模型

基于以上分析，通過測量主軸電機電流來間接測量切削力是合理可行的。因此，本文選擇主軸電機電流I代替切削力作為狀態監測參數，以及進給速度的變化作為系統調整量，以電流作為決策量構成加工系統的閉環反饋控制，最終實現切削力自適應控制。數控加工切削力自適應控制系統模型如圖2所示。根據模糊控制原理，該控制系統的兩個輸入參數分別為電流偏差和偏差變化率，系統輸出則為進給速度調整量。圖中，FLC為模糊控制器，CNC_Mach為被控數控機床，I為實際電流信號，Iref為給定的電流參考值。在任一采樣時刻輸入到CNC_Mach的進給量為

圖2 基于模糊邏輯的數控加工自適應控制系統模型

3 模糊控制器

模糊控制器結構如圖3所示，它由輸入參數模糊化、模糊推理、隸屬函數、模糊規則庫和輸出反模糊化組成。依前述，模糊控制器輸入語言變量為電流偏差E及偏差變化率EC，輸出語言變量為進給速度變化U。

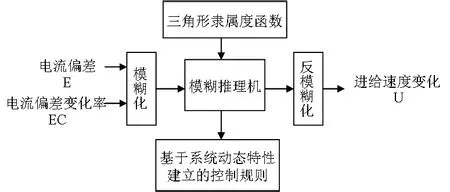
圖3 模糊控制器結構

3.1 輸入模糊化和隸屬函數

為了得到系統的輸入量，電流參考值Iref為設定值，被監測電流值I為數控加工實際電流值。任一采樣時刻i，I與Iref的比較得到模糊控制器的兩個輸入參數：

現取E，EC和U的模糊子集為{NB，NM，NS，0，PS，PM，PB}，其中NB，NM，NS，0，PS，PM，PB分別表示為負大、負中、負小、零、正小、正中、正大，令這三個語言變量的模糊集合論域量化檔數均取相同值6，論域均為{-6，-5，-4，-3，-2，-1，0，+1，+2，+3，+4，+5，+6}；為減少計算量加快響應速度，隸屬函數均以三角形函數表示，如圖4所示。

圖4 隸屬度函數

3.2 控制規則

1）經驗控制規則

如圖4所示，輸入參數電流偏差和偏差變化率的模糊集為7，每一組輸入模糊集的組合都對應一種控制動作，具體動作由模糊控制規則來決定，例如，根據經驗知識和實驗結果，如果電流低于目標值，進給速度就應該增加，根據決策量與被控目標的聯系，目前，大多數都是基于專家和知識經驗建立的模糊控制規則，如表1所示[2,9]。

表1 基于經驗的控制規則表

2）基于動態特性優化的控制規則

由于數控加工系統動態非線性的特點，依據經驗建立的規則庫往往不能正確反映輸入輸出之間真實的動態關系，因此，本文在此基礎上，進行優化和重新建立規則庫，以提高模糊控制器的性能，使得加工過程快速穩定及避免機床承受大的沖擊。

文獻[23]研究了數控加工主軸-X軸切削系統動態特性，得到了系統從啟動到穩態的動態仿真結果，從結果中得到，當主軸電機電流發生較大幅度變化時，進給速度變化較平緩，并且，主電機電流和進給速度變化是本文模糊控制器的輸入和輸出語言變量，兩者之間的變化關系決定了模糊控制規則，因此這種變化趨勢為控制規則的優化和建立提供了理論依據。基于兩者的變化關系，將其量化，即把輸入空間到輸出空間的推理以量化的形勢進行表達，得到輸入和輸出語言變量電流偏差E、偏差變化率EC和進給速度變化U三者之間的數值變化關系，如表2所示。當電流偏差E為NM，偏差變化率EC為NM時，進給速度變化U為NB，而基于經驗的模糊控制規則中，此時進給速度變化U為NM。基于動態特性得到輸入輸出語言變量變化關系共6組，基于此，對基于經驗的模糊控制規則逐一對照進行優化；再根據控制規則的基本原則，修改其他規則，如：當電流偏差E為PM，偏差變化率EC為PB時，進給速度變化U為PM，因此，當電流偏差E為PS，偏差變化率EC為PB時，進給速度變化U也應改為PM。根據以上分析，最終建立新的模糊控制規則如表3所示。

表2 輸入輸出語言變量變化關系模糊量化表

表3 基于系統動態特性建立的控制規則

對比表1與表3可以看出，輸入、輸出語言變量總體變化趨勢相同，個別地方存在差異；例如：當電流偏差E的語言變量值為NB，EC的語言變量值為NS時，基于經驗的控制規則中U的語言變量值為NM，而優化后為NB；當E、EC都為NS時，基于經驗的控制規則中u的語言變量值為NS，而優化后為NM。從變化趨勢上看，當輸入參數值呈增加趨勢時，輸出參數值也呈增加趨勢，但增加速度較緩；由此可見優化后的控制規則更加符合輸入、輸出參數真實的動態變化關系，故模糊控制器性能更佳。此外，作為模糊控制器輸入輸出語言變量的主電機電流和進給速度變化兩者之間的變化關系是基于系統動態特性研究得到，當系統參數發生變化時，兩者的變化關系和趨勢不變，因此，基于此建立的模糊控制規則是合理且穩定的。

3.3 模糊推理和輸出反模糊化

根據已建立的模糊規則及隸屬度函數，經過模糊推理，輸出控制量，再通過反模糊化，產生模糊控制動作，因此，模糊推理和反模糊化決定了模糊輸入參數所對應的模糊控制規則和隸屬度函數的執行效果。采用重心法對控制量的模糊集進行反模糊化，得到輸出參數進給速度的變化調節量。

其中，Δafi為第i條規則時的輸出，Hi為隸屬度函數，n為控制規則總數。

4 實驗驗證

4.1 單工序加工實驗

數控銑削參數在線優化實驗在TDNC-W200數控銑床進行，如圖5所示，機床設備和實驗參數如表4所示。

圖5 實驗機床

表4 數控銑削加工參數在線優化單工序加工實驗參數

1）既定切深下動態特性優化控制規則與經驗控制規則在線優化效果比較

為了安全起見，將既定電流值設定為7.6A，電流偏差E實際取值范圍為[-1，1]，偏差變化率EC實際取值范圍為[-2，2]，輸出進給倍率變化量U實際取值范圍為[-40，40]，模糊控制程序中分別采用經驗控制規則表1和基于動態特性優化建立的控制規則表3。以1mm切深為例，實驗結果分別如表5、圖6和圖7所示。實驗過程中為了充分體現出效果，選擇的主軸轉速不同，初始進給速度不同，因此初始電流值也不同，但無論是降速還是升速都能調節到既定安全值。從圖中可以看出，基于動態特性優化的控制規則在線調節時間為30s，而基于經驗的控制規則在線調節時間為60s，可見基于動態特性優化控制規則的參數在線優化時能夠更快地使機床參數調節到設定值和穩定狀態。

表5 兩種不同控制規則優化效果

圖6 動態特性優化控制規則降速和升速

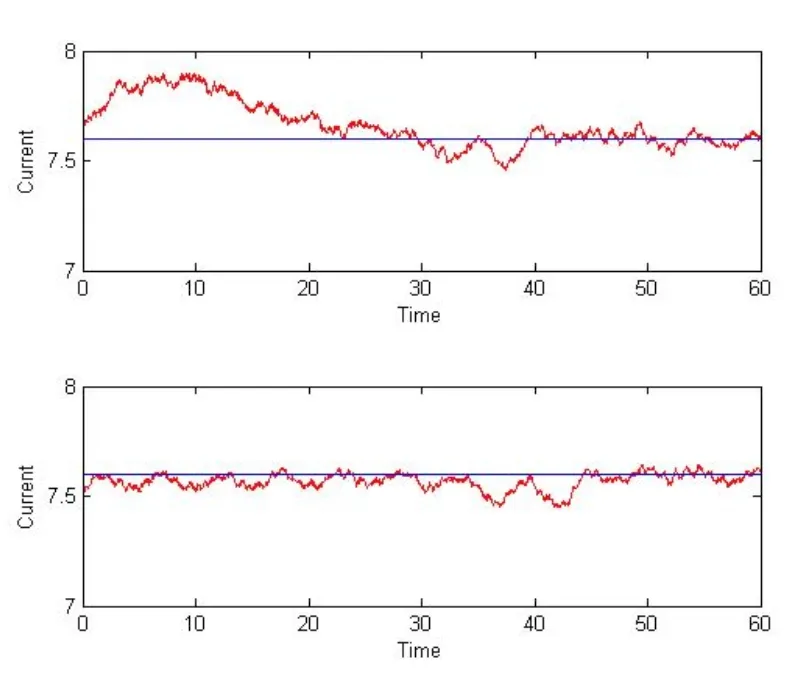
圖7 經驗控制規則降速和升速

2）變切深下動態特性優化控制規則與經驗控制規則在線優化效果比較

根據機床參數，設定既定電流值為7.8A，確定模糊輸入語言變量電流偏差的變化范圍為[-8，8]，電流偏差變化率的范圍為[-16，16]；輸出語言變量進給倍率變化的范圍為[-150，150]；分別按照0.5mm，1mm，1.5mm，2mm的切深參數順序進行平面銑削，進一步驗證動態特性優化規則的優化效果。加工實驗過程分別如圖8和圖9所示。

圖8 采用經驗規則加工過程

圖9 采用動態特性優化控制規則加工過程

表6和表7所示分別為采用經驗控制規則和動態特性優化控制規則進行的在線優化結果。從表中看出，相同的切削參數，當切深改變時，基于經驗規則電流值變化較大，超出設定值，通過再次自適應調整到既定值；而采用優化控制規則，進給速度調整緩慢，電流恰好達到既定值附近，不會反復調整。例如，當切深為0.5mm時，采用經驗控制規則在線調整進給速度，電流達到8.2A，超出設定值，再次進行自適應調整，降低進給速度，使得電流達到7.8A，完成本工序需要40秒；而采用動態特性優化控制規則則需要30秒，節省了10秒。因此，優化后的控制規則相對于經驗控制規則能夠使得電流值更快地穩定到設定值，提高模糊控制器的性能，更能提高加工效率，同時也驗證了方法的有效性和可行性。

表6 基于經驗控制規則優化效果

表7 基于動態特性優化控制規則優化效果

4.2 實體模型加工實驗

為了充分驗證在線模糊自適應優化功能，體現在線調整主電機電流，穩定切削力的效果，根據加工時刀具走刀順序和加工路線，根據切削負載不同，導致電流不同，設計能夠使得電流變化的加工模型，如圖10所示，單邊實體邊長為26mm，輪廓總長260mm，厚5mm的實體模型。以連續加工實體模型為例，觀察在整個加工過程中，當主電機電流即切削力超出或達不到預定值時，通過在線模糊控制，使得電流調整到設定值，保證加工穩定性，同時使得機床能發揮最大效率。螺旋銑削實體模型實驗在TDNC-W200數控機床上進行，加工基本實驗參數如表8所示。

圖10 實體模型尺寸

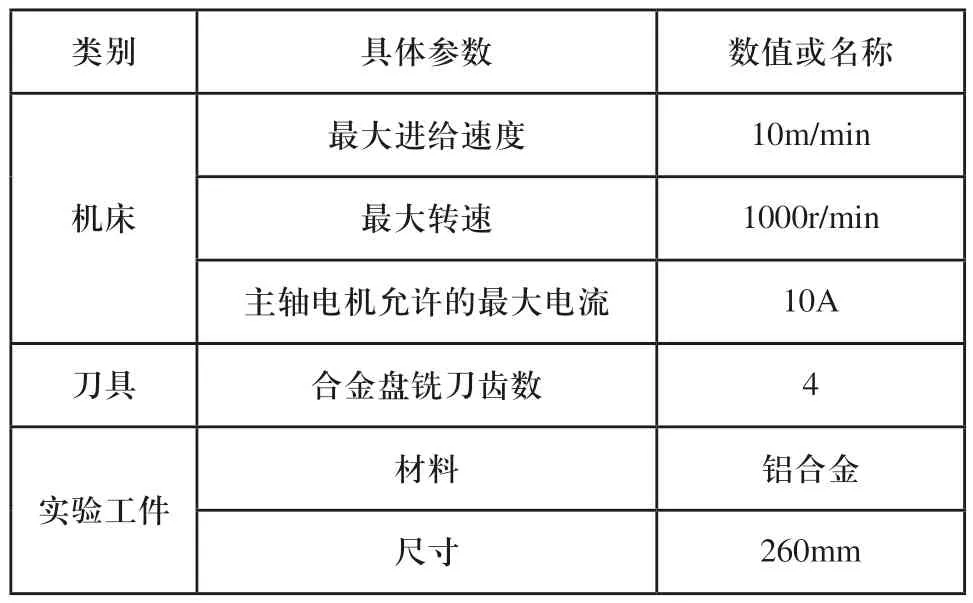
表8 實體模型加工參數在線優化實驗參數

如表9所示，根據實際切削條件設定加工參數，選擇的是加工最大輪廓時的數據，每層切深為1mm，共切削三層。為了安全起見，設定電流值為7.6A，因此相對應的進給速度較低，導致總體加工時間較長，為660s。但自加工始，系統即開始采集電流，在t＝10s時啟動模糊控制，由于此時的主電機電流值高于設定值，所以在模糊控制的作用下，調整進給速度，使得電流下降到既定值，由圖11可以看出，電流在100s時調整到既定值；同時由于走刀順序，加工空行程時切削電流低于設定值，系統自動進行上調，直至穩定在設定值附近，使得機床電流即切削力一直處在額定負載狀態，提高加工效率和穩定性，發揮機床最大功效。加工過程和效果如圖12所示。

表9 實體模型加工參數在線優化實驗結果

圖11 實體模型加工電流在線調整過程

圖12 實體模型加工過程和效果

5 結論

本文提出了一種基于數控加工系統動態特性的參數在線自適應優化方法。該方法基于系統動態特性研究得到更加接近真實切削狀態下的模糊控制器輸入輸出語言變量間變化關系，從而確定了輸入空間到輸出空間的推理，據此對基于經驗的控制規則進行優化，當電流發生突變時，通過模糊控制器作用，進給速度得到在線自適應優化，使得電流盡快回歸到設定值附近。優化后的控制規則提高了控制器的性能，更快地使數控加工切削力調整到既定值，提高加工效率，更大地發揮機床功效，同時達到保護機床和刀具的目的，最后通過實驗證明該方法的可行性。