扶壁式擋墻抗采動變形性能優化研究

吳振 張春麗

摘 要：本文應用ANSYS 有限元分析軟件，通過對采動區扶壁式擋墻采用數值模擬計算得出了合適的豎板厚度、底板厚度、擋墻長度和扶板間距，為扶壁式擋墻的設計提供有效的依據。

關鍵詞：采動區;扶壁式擋墻;數值模擬;優化研究

中圖分類號：U417.1? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? 文章編號：1006—7973（2019）08-0108-02

1引言

近幾年來，隨著我國經濟建設的發展，道路建設越來越多，然而由于我國礦產資源豐富，在這些資源被開采所造成的地表變形會對道路造成影響。目前對于扶壁式擋土墻的研究，主要集中在傳統高填方邊坡上，對于采動區高填方邊坡支擋研究較少。本文利用ANSYS有限元軟件，通過建立三維模型，對扶壁式擋墻結構在采動狀態下進行研究，得出擋墻豎板厚度、底板厚度、擋墻長度和扶板間距變化時擋墻的最大主應力變化規律，為扶壁式擋墻的設計提供有效的依據。

2有限元計算模型的建立

2.1 基本假設

（1）采用三角函數法施加在模型的底邊界上用以模擬采動影響下的地基不均勻沉降。

（2）不考慮孔隙水壓力的影響。

（3）為簡化模型計算，地基土為一種土體，土體為均質各向同材料。

2.2 計算模型

ANSYS所建模型包括擋土墻、土體等主要部件。根據扶壁式擋墻的設計特點和工程條件，單段擋墻高度為10m，墻趾寬2m，墻踵寬度4m，擋墻豎板厚度，底板厚度，擋墻長度和扶板間距為變化值。擋墻下兩側土體長度各取40m，擋墻下土體高度20m。如圖1所示。

2.3 計算參數

本模型材料計算參數見表1。

3 計算結果與分析

為消除先期固結應力的影響，使用先導出初應力，再將其導入的方法。在考慮重力作用的情況下，可以保證所建模型的尺寸和初始應力狀態與實際情況相符。運用數值模擬方法，分別研究擋墻豎板厚度，底板厚度，擋墻長度和扶板間距變化時擋墻的最大主拉應力變化規律，從而得到擋墻的最優化結構數值。主要分成四個部分：

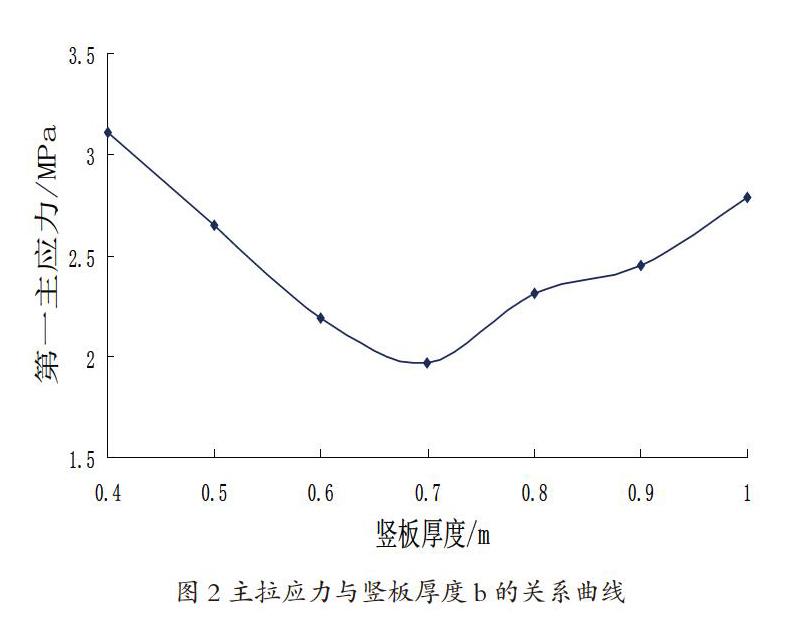
（1）圖2擋墻高度和長度一定，擋墻豎板厚度變化的情況，豎板厚高比b/H分別取0.04～0.1。

（2）圖3擋墻高度和長度一定，擋墻底板厚度變化的情況，底板厚度h分別取0.4～1.0。

（3）圖4擋墻厚度一定，擋墻長度變化的情況，長高比L/H為0.7～1.3。

（4）圖5擋墻厚度和長度一定，擋墻扶板間距變化的情況，扶板間距D與擋墻長度比值D/L分別取0.1～0.7。

由圖2可以看出，擋墻高度和擋墻長度等不變的情況下，當調節豎板厚度時，最大主拉應力分布曲線呈先減小后增大的趨勢，扶壁式擋墻在豎板厚度b為0.7m時，主拉應力最小且在結構等效最大拉應力范圍內。

由圖3可以看出，擋墻高度和擋墻長度等不變的情況下，當調節底板厚度h時，最大主拉應力分布曲線呈先減小后增大的趨勢，扶壁式擋墻在h為0.8m時，主拉應力最小且在結構等效最大拉應力范圍內。

由圖4可以看出，擋墻高度和厚度等不變的情況下，當調節擋墻長度時，最大主拉應力分布曲線呈先減小后增大的趨勢，扶壁式擋墻在擋墻長度L為10m時，主拉應力最小且在結構等效最大拉應力范圍內。

由圖5可以看出，擋墻豎板以及底板厚度和擋墻長度等不變的情況下，當調節扶板間距時，最大主拉應力分布曲線呈先增大再減小后增大的趨勢，扶壁式擋墻在扶板間距D為3m時，主拉應力最小且在結構等效最大拉應力范圍內。

4 結論

本文應用有限元數值模擬及其理論分析等方法，對采動區扶壁式擋墻抗變形結構進行研究，得出以下主要結論：

（1）在負曲率變形作用時，扶壁式擋墻在豎板厚高比b/H為0.07時，主拉應力最小且在結構等效最大拉應力范圍內。

（2）在負曲率變形作用時，扶壁式擋墻在底板厚度h為0.8m時，主拉應力最小且在結構等效最大拉應力范圍內。

（3）在負曲率變形作用時，扶壁式擋墻在擋墻長高比L/H為1.0，D/L為0.3時，主拉應力最小且在結構等效最大拉應力范圍內。

參考文獻：

[1] 柏永生.采動區雙面加筋土擋墻力學特性研究[D]. 江蘇徐州，中國礦業大學，2008.

[2] 陳桂林. 樁承扶壁式擋墻在深厚填土地基中的應用[J]. 福建建設科技， 2009，6：15-17.

[3] 李永樹，韓麗萍.采動沉陷對建筑物的破壞作用[J]. 河北煤炭建筑工程學院學報， 2004，2：48-51.

[4] 煤炭科學研究總院唐山分院.抗變形結構理論計算方法[J]. 1993： 24～40

[5] 馬石城，鄒銀生，王貽蓀. 不同土壓力下懸扶壁式擋土墻抗傾覆穩定比較[J]. 建筑科學，2006，16（6）：117-121.