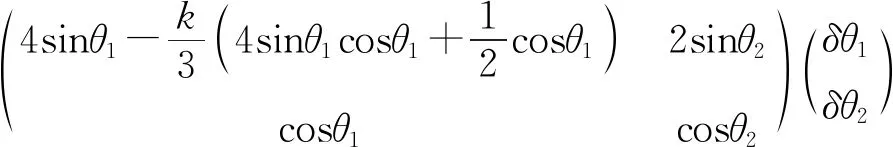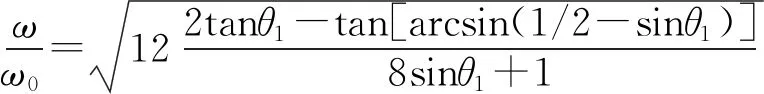正五邊形平衡位形能取到嗎?
林倩茹 吳靜燕 邱為鋼
(湖州師范學院理學院, 浙江 湖州 313000)
奧賽物理題選中有這樣一道題:5根相同的勻質細桿,用質量密度均可忽略的光滑鉸鏈兩兩首尾相接連成一個五邊形,將其中一個頂點懸掛在天花板下,試求平衡時此五邊形的五個頂角.又如在最下邊的細桿中點再懸掛一個重物,能否使五個細桿構成一個等腰三角形?原題是用受力分析做的,想在下面加一個向下的力,使得五邊形能變為三角形,但沒成功.那么有沒有向外的力,可以拉伸使得五邊形木桿平衡時,變為三角形或正五邊形.中學物理所熟悉的這種力是轉動參考系下的慣性離心力.本文木桿體系轉軸都是對稱軸,根據文獻[2],這樣的勻角速狀態可以稱為平衡態.我們從能量角度考慮這種平衡態,即體系的重力勢能和轉動參考系下的離心勢能之和,平衡態使得總勢能取得極小.我們發現,當用線拎起木桿并使之勻速轉動達到平衡時,取適當的角速度,五邊形木桿的平衡位形可以取到等腰三角形和正五邊形,彌補了文獻[1]的遺憾.
先推導以z軸為轉軸的轉動參考系下,任意放置理想木桿的離心勢能與端點坐標的表達式.設木桿兩端坐標是(x1,z1)和(x2,z2),長度是L,桿上任意一點的坐標矢量是
r(s)=(1-s)(x1i+z1k)+s(x2i+z2k).
(1)
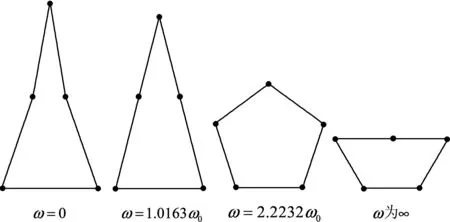
其中參數s的取值范圍是0 (2) 積分計算得到整個桿離心勢能為 (3) sinθ1+sinθ2=1/2. (4) 把桿端點坐標代入式(3)計算離心勢能,再加上重力勢能,得到五邊形桿總勢能為 (5) 五邊形桿繞對稱軸勻速轉動達到平衡時,木桿傾角變化引起總勢能的變化為0, δΦ5=4sinθ1δθ1+2sinθ2δθ2- (6) 幾何約束條件式(4)的變化也是0, cosθ1δθ1+cosθ2δθ2=0. (7) (6)式和(7)式可以寫成矩陣形式 (8) 由幾何約束條件(4)式,兩個角度的變化不是獨立的,(8)式存在非零解的必要條件是系數矩陣的行列式為0.計算得到 (9) 當轉速參數k=0時,式(9)就退化到文獻[1]中的結論.依據式(4),把θ2消去,得到轉速與右邊第一個木桿傾斜角θ1的關系式 (10) 角速度為0時,傾角θ1為α=0.172242.隨著角速度增大,傾角θ1逐漸增大.角速度趨向無窮大時,傾角θ1趨向于π/2,所以傾斜角θ1的取值范圍是α<θ1<π/2. 當轉動五邊形的平衡位形是等腰三角形時,θ1=arcsin(1/4),由(10)式,角速度 當轉動五邊形的平衡位形是正五邊形時,θ1=3π/10,由(10)式,角速度 圖1 不同轉速下五邊形木桿的平衡位形 由此可見,當角速度取合適值時,轉動五邊形的平衡位形是可以取正五邊形的.不同轉速下五邊形桿的平衡位形如圖1所示.