基于卡爾曼濾波離散滑模控制的明輪船直線跟蹤

洪劍青 趙德安 孫月平 張 軍 劉 波 劉曉洋

(1.江蘇大學電氣信息工程學院， 鎮江 212013； 2.鎮江高等專科學校現代裝備制造學院, 鎮江 212028)

0 引言

隨著人民生活水平的提高，人們對水產品的需求不斷增長，極大地促進了水產養殖業的飛速發展[1-3]。水產養殖業已成為國民經濟不可缺少的組成部分，年產值高達幾百億元。規模化生產促使水產養殖業向集約化、自動化、信息化、智能化的方向發展[4-7]。

養殖水域通常水情比較復雜，水下植物較多。明輪船具有吃水淺、適航性好的特點，適宜作為水面作業裝備的載體。水上作業裝備實現智能化、自動化、信息化作業的方式，不僅可以提高作業效率、降低人力成本，克服工作時間的限制，且更加貼近養殖動物的生活習性[8-9]。

明輪船的航跡跟蹤是近來研究的熱點。文獻[9]建立了明輪船的水動力模型和控制方程。文獻[8，10]詳細給出明輪船航跡跟蹤系統的硬件方案和模糊控制航跡跟蹤方法[8,10-12]，實現了基本的跟蹤。文獻[13-14]采取魯棒預測控制、障礙李亞普諾夫函數法，取得較好的控制效果，但是由于預測控制采取在線連續時域滾動計算，算法復雜、計算量較大、計算耗時和對系統計算資源需求較高、對反饋信號實時性要求較高；障礙李亞普諾夫函數法存在反步微分爆炸的可能，且控制方法未對反饋信號進行處理，實際使用中發現信號擾動較多，易造成執行器過多的不必要主動控制動作，會導致控制效果變差，浪費有限船載電能，縮短續航里程。文獻[15]采取了PD控制對航跡跟蹤，由于陸地行駛車輛無風浪干擾，PD控制對于陸地行走的車輛跟蹤效果較好，對于受風浪不斷干擾的明輪船而言，跟蹤效果較差。因此，克服擾動對航跡跟蹤的影響、降低控制運算量、提高系統穩定性是明輪船航跡跟蹤研究的關鍵[16]。針對實際狀況，本文提出一種運算量較小的基于卡爾曼濾波的離散滑模控制方法實現明輪船的直線跟蹤。

1 航跡跟蹤系統建模

明輪船的航跡跟蹤屬于欠驅動水面運動系統。采用船舶運動坐標系，其運動方程[9-10,17]為

(1)

其中

ν=[vr]T

式中m——明輪船質量，kg

xG——明輪船重心坐標，m

u0——明輪船航行速度，m/s

Iz——明輪船質量對z軸的慣性矩，kg·m2

v——橫漂速度，m/s

r——轉艏角速度，(°)/s

δR——明輪船虛舵角，(°)

航跡跟蹤的核心是控制明輪船的船艏航向。通過調整艏搖角使明輪船的航跡偏差不斷得到糾正。根據文獻[9-10]，船舶運動時呈現非常大的慣性，因提供給明輪船控制船艏運動方向的能量有限，通常角速度低于3(°)/s，船舶運動具有低頻特征，可以描述為一階微分方程。在忽略橫漂速度v的基礎上，采取野本一階模型(Nomoto)的形式[17-19]，給出明輪船的艏搖角速度系統傳遞函數為

(2)

其中

det(N(u0))=Yv(Nr-mxGu0)-Nv(Yr-mu0)

式中n11、n21——明輪船附加質量水動力系數

b1、b2——明輪船轉艏水動力系數

T——穩定性系數

K——回轉性系數

2 船艏運動的離散滑模控制

滑模變結構控制策略可以使系統“結構”具有隨時間變化的開關特性。迫使系統沿著規定軌跡作高頻、小幅運動實現滑動模態。離散滑模控制是滑模控制數字化方式[20-21]。滑模控制器設計如下。

首先將艏搖角運動傳遞函數轉換為狀態方程并離散化，得到離散艏搖角運動狀態方程

x(k+1)=Ax(k)+Bu(k)

(3)

式中A——狀態矩陣B——輸入矩陣

x(k+1)、x(k)——系統在k+1、k時刻的狀態

u(k)——系統在k時刻的輸入量

設計切換函數為

s(k)=Cex(k)

(4)

式中Ce——控制參數

s(k+1)=s(k)=Cex(k+1)=CeAx(k)+CeBu(k)

(5)

根據文獻[20]，設計離散滑模控制器u(k)為

u(k)=ueq(k)+FDx(k)

(6)

其中

ueq(k)=-(CeB)-1Ce(A-I)x(k)

(7)

FD=[f1f2…fn]

式中f1、f2、…、fn表示系統各狀態變量的增益，I表示單位矩陣。

根據文獻[20]，定義Lyapunov函數為

(8)

由式(5)～(7)得到

s(k+1)=CeAx(k)-Ce(A-I)x(k)+CeBFDx(k)=
Cex(k)+CeBFDx(k)=s(k)+CeBFDx(k)

s2(k+1)-s2(k)=2s(k)CeBFDx(k)+

(CeBFDx(k))2

(9)

根據Lyapunov穩定性定理，s(k)=0為全局穩定平衡面，任意初始位置的狀態都會趨向切換面s(k)。取到達條件為

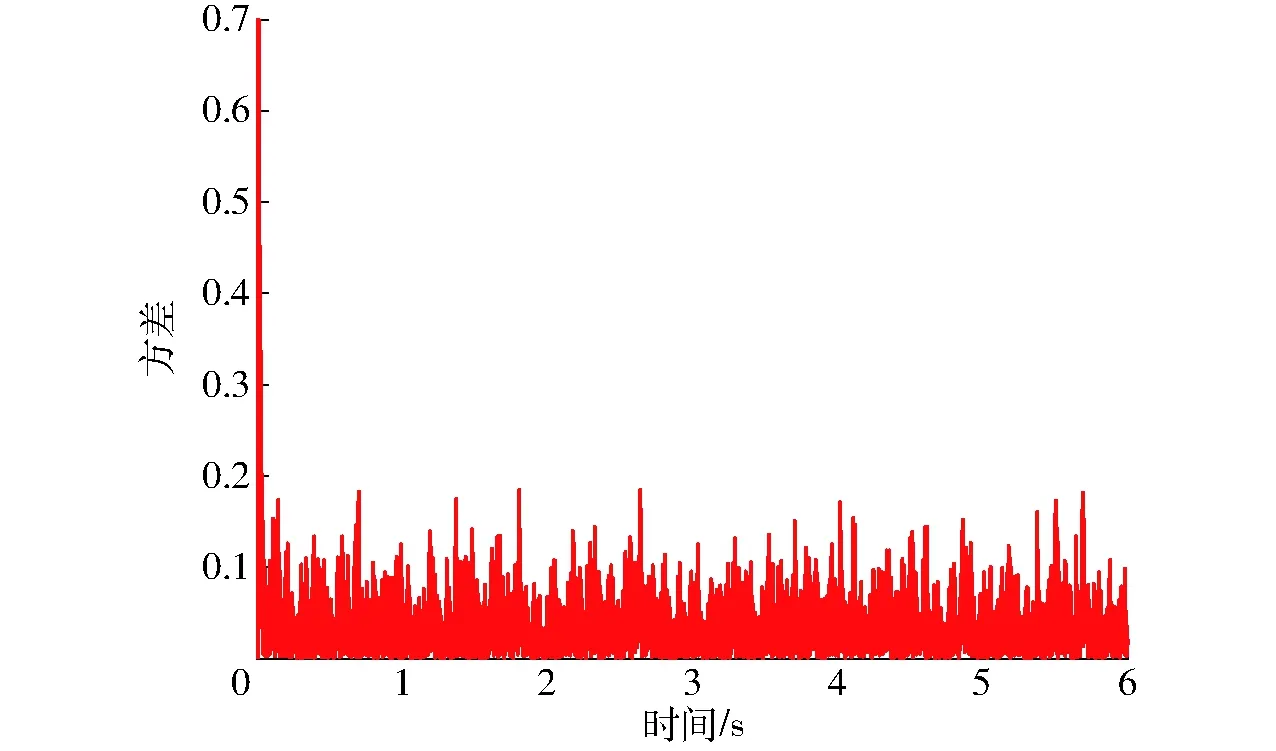
s2(k+1)

(10)

則由式(9)可得

(CeBFDx(k))2<-2s(k)CeBFDx(k)

即

取|fi|=f0，f0>0，則對于每一個i，有

(11)

定義

(12)

將式(12)代入式(11)得到

(13)

可得

(14)

即

(15)

只要滿足式(15)即可滿足條件式(10)。

由式(12)和式(15)得

即

(16)

滿足式(16)條件，確定f0。

綜上所述，離散滑模控制率為式(6)、(7)、(16)，即

(17)

則系統穩定。

3 卡爾曼濾波

明輪船在航行過程中不斷受到風、波浪的干擾，船艏的艏搖角度始終處于小幅波動狀態。文獻[18]認為風浪對船舶航行的干擾主要由周期為5～20 s的長波疊加組成。部分二階波引起的振蕩可以通過自動航向糾偏抵消，而一階波形引起的振蕩和運動超出了自動駕駛儀的工作頻帶，會引起自動駕駛設備的高頻運動，需要通過濾波的方式降低一階波形的干擾。

船舶運動控制采取的濾波的方式主要有低通濾波、帶通濾波、級聯陷波濾波、基于觀測器的濾波器等。雖然前述濾波可以降低風浪造成的干擾振蕩，但是存在“相位滯后”的問題。經仿真、實際使用，發現此“相位滯后”極易引發系統振蕩，造成航行的不穩定。

卡爾曼濾波能夠從噪聲污染的測量信號中，采用遞歸方式估計動態系統的真實狀態，有效地避免了“相位滯后”。在雷達、通訊、導航、目標跟蹤領域被廣泛使用。若系統離散狀態方程為[14,17]

(18)

式中X——系統狀態矩陣

Φ——系統矩陣

H——觀測矩陣Y——系統輸出

W(k)——輸入噪聲

Z(k)——觀測噪聲

Γ——噪聲驅動矩陣

其卡爾曼濾波增益的計算過程為：

(1)狀態一步預測

(k+1|k)=Φ(k|k)

(2)狀態更新

(k+1|k+1)=(k+1|k)+Ka(k+1)ε(k+1)

其中

ε(k+1)=Y(k+1)-H(k+1|k)

式中ε——系統實際輸出與觀測估計輸出的誤差

Ka——卡爾曼濾波增益

(3)濾波增益矩陣

Ka(k+1)=P(k+1|k)HT(HP(k+1|k)HT+R)-1

式中P——協方差矩陣R——Z(k)的方差

(4)一步預測協方差矩陣

P(k+1|k)=ΦP(k|k)ΦTΓQΓT

式中Q——W(k)的方差

(5)協方差陣更新

P(k+1|k+1)=(In-Ka(k+1)H)P(k+1|k)

式中In——單位對角陣

初始條件

式中μ0——系統狀態初始值

P0——協方差矩陣初始值

卡爾曼濾波將系統模型引入濾波過程，通過狀態估計方差計算卡爾曼增益，反復迭代得到最優狀態估計。且由于離散卡爾曼濾波不需要存儲大量歷史數據，適合計算機工作。明輪船的航跡跟蹤和航向保持需使用二維卡爾曼濾波，故對艏搖角及艏搖角速度進行二維濾波。

4 控制系統結構設計與仿真

明輪船艏搖角跟蹤控制系統的結構如圖1所示。

圖1 艏搖角跟蹤控制系統Fig.1 Yaw angle tracking control system

電子羅經和慣性導航設備給出明輪船當前航向角ψ、艏搖角速度r，經卡爾曼濾波后進行負反饋，得到濾波降噪后的當前航向角、艏搖角速度，航向控制器根據給出的目標航向角ψd，結合負反饋信號進行計算、經過左右明輪轉速分配器分配后，得到左右明輪的各自轉速nl和nr。左右電動機轉速控制器根據給定的左右明輪的各自轉速nl和nr，給出驅動左右電動機的信號ul和ur驅動電動機。電動機的轉速信號n1、n2經負反饋，形成轉速閉環控制。據此推轉左右明輪，驅動船體運動。

為驗證算法有效性，使用Matlab軟件進行計算機仿真測試。根據明輪船的試驗艇參數，建立明輪船艏搖角動態響應模型[10]。根據控制系統結構建立明輪船艏搖角仿真系統，如圖2所示。

圖2 明輪船艏搖角仿真系統Fig.2 Paddle wheel ship yaw angle simulation system

根據上述仿真系統結構，將仿真程序輸入Matlab計算機軟件系統進行動態響應仿真，得到仿真結果。仿真過程中，使用正弦信號作為跟蹤目標信號。對控制系統跟蹤信號不僅有位置誤差的要求，還有速度誤差的限制。不施加干擾時的跟蹤效果如圖3所示。

圖3 無干擾跟蹤效果Fig.3 Tracking effect without interference

圖3顯示了明輪船船艏采用滑模控制方式與采取純PD控制方式時船艏對目標偏航角的跟蹤效果，二者差距顯著。兩種控制方式的初始狀態角度是1.5°。跟蹤目標信號是從0°開始的正弦信號。仿真結果顯示離散滑模控制能夠快速跟蹤目標信號。由于滑模算法的快速跟蹤特性，使得采取滑模算法時，控制信號在初始階段存在短時間的過飽和現象，可以通過限制控制信號輸出幅值的方式進行消減。PD控制對目標的跟蹤是逐步逼近，振蕩收斂，實現最終的跟蹤效果慢了許多。

抗干擾檢驗時，在仿真系統的輸出信號上施加無量綱高斯噪聲信號，得到在干擾下的艏搖角跟蹤仿真結果，如圖4、5所示。

圖4 有干擾跟蹤仿真結果Fig.4 Tracking effect with interference

圖5 有干擾跟蹤仿真方差Fig.5 Interference tracking simulation variance

仿真結果表明：離散滑模控制在高斯噪聲干擾作用下，依然可以控制船艏進行航向跟蹤，但是跟蹤過程諧波較大，有干擾無濾波跟蹤結果與目標信號的無量綱方差達到0.4。可以預見干擾會導致欠驅動系統明輪船艏做出幅度較大、頻率較高的頻繁控制動作。這對明輪船驅動設備、續航時間都會產生不利影響。

引入卡爾曼濾波降噪后的仿真結果表明，施加相同量級的高斯噪聲干擾，跟蹤信號的諧波幅值大幅度降低，如圖6、7所示。

圖6 有干擾濾波跟蹤仿真結果Fig.6 Interference filter tracking simulation results

圖7 有干擾濾波跟蹤仿真方差Fig.7 Interference filtering tracking simulation variance

經數據分析，在加入卡爾曼濾波之后，跟蹤信號與目標信號的無量綱方差降低到0.18。顯然，卡爾曼濾波的引入，對干擾起到了抑制與降低。這對于明輪船延長續航時間、降低控制系統不必要的高頻動作作用明顯。

5 試驗

為驗證算法的可行性，采用實際樣船進行算法適航性驗證。經測量獲取明輪船參數，計算相關水動力參數。試驗明輪船見圖8。

圖8 明輪船樣船Fig.8 Paddle wheel ship

將離散滑模算法的控制代碼輸入控制系統，并反復進行調試、試驗。試驗當天多云，風力3～4級，氣溫15～24℃。得到轉艏運動試驗動態響應結果如圖9所示。

圖9 轉艏動態響應曲線Fig.9 Dynamic response curves

試驗曲線顯示了明輪船轉艏運動、直線運動的艏搖角動態變化過程。開始階段是轉艏運動，艏搖角急速拉升。經圖9的試驗結果分析，離散滑模控制方式下偏航角的最大超調量較PD控制方式減小25%，調整時間減少50%。受制于明輪船轉艏運動過程的艏搖角速度限幅和執行電機輸出飽和限制的影響，轉艏運動的快速性、超調量不及仿真效果，但是明輪船的直線跟蹤效果達到預期，直線跟蹤偏差效果見圖10。

圖10 明輪船直線跟蹤偏差Fig.10 Paddle wheel ship linear tracking deviation

從圖10可見，明輪船進入直線軌跡跟蹤時，由于轉艏運動，跟蹤軌跡切換造成跟蹤目標不定，致使明輪船剛進入直線段航跡點時出現較大偏差。隨后，明輪船完全進入直線段目標軌跡區域航行，由于引入卡爾曼濾波滑模算法，直線跟蹤偏差均在10 cm以內，達到直線跟蹤目標要求。由于跟蹤過程存在陣風干擾，明輪船被風力推向偏航。設計的濾波滑模控制算法進行了糾偏操作，使明輪船沿著目標軌跡航行。分析圖10的試驗數據，離散滑模控制實現的明輪船直線航跡在剛進入直線段時，快速逼近目標軌跡，在風浪干擾的作用下，最大偏差只是瞬間超過10 cm，其他時間段均低于10 cm，遠優于PD控制實現的效果。

無風浪干擾時，無卡爾曼濾波PD控制算法的跟蹤精度雖然滿足要求，但是收斂速度較慢。當出現風浪干擾時，明輪船出現較大的偏航，在無濾波的PD控制算法作用下，最終也能糾偏，但是航行過程的波動較大，最大偏差達到0.35 m，收斂到滿足偏差要求的航跡時間也較長。實際航行試驗表現為在目標航跡附近多次振蕩。

有卡爾曼濾波的滑模航跡跟蹤控制算法，在跟蹤精度滿足要求時，跟蹤過程更加平穩，收斂速度更快。這對于明輪船工作過程的穩定性、節能降耗、延長續航時間起到重要作用。

6 結論

(1)采用離散滑模控制方式對明輪船的轉艏運動進行控制。通過建立轉艏運動模型，進行了離散滑模控制仿真，證明離散滑模算法可以對明輪船的轉艏運動、直線跟蹤進行有效控制。

(2)對干擾采取了卡爾曼濾波進行消減。仿真結果說明，卡爾曼濾波可以有效抑制航行過程中風力、波浪對航跡跟蹤造成的干擾，對提升系統控制過程的平穩、節能降耗、延長續航起到重要作用。

(3)對算法進行了試驗驗證。轉艏運動在算法控制下，均能實現直線跟蹤。結果表明，采取基于卡爾曼濾波的滑模控制方式較PD控制，艏搖角的最大超調量比PD控制方式減小25%，調整時間減少50%，航跡偏差低于10 cm。由于轉艏運動的角速度限幅、執行電機的飽和特性限制，明輪船的大角度轉艏動態響應特性不及仿真效果，但目標軌跡跟蹤效果達到預期。