水輪機尾水管渦帶壓力脈動同步及非同步特性研究

孫龍剛 郭鵬程 羅興锜

(西安理工大學(xué)省部共建西北旱區(qū)生態(tài)水利國家重點實驗室， 西安 710048)

0 引言

隨著風(fēng)能、太陽能等間歇性能源在電網(wǎng)中比例的增加，水電機組將更多地運行在變負荷工況及偏工況下以平衡電網(wǎng)參數(shù)[1-2]。偏工況下運行，水輪機不可避免地經(jīng)歷動態(tài)負荷不平衡，激發(fā)高幅值壓力脈動、水力振動、噪聲等，嚴重影響水輪機運行穩(wěn)定性[3-5]。尾水管渦帶(Precessing vortex rope,PVR)是混流式水輪機在部分負荷工況運行時尾水管水流中出現(xiàn)的一種強烈偏心螺旋狀渦旋運動，渦帶頻率約為轉(zhuǎn)頻0.2～0.45倍并激發(fā)高幅值壓力脈動。尾水管渦帶的形成有兩個主要因素：較大的角動量與軸向動量比產(chǎn)生的強烈渦旋流動；與轉(zhuǎn)輪出口速度及錐管段擴散形式有關(guān)的軸向方向逆壓梯度[6]。它是混流式水輪機運行在偏工況下的一種固有水力特性，是水力不穩(wěn)定性的表征和結(jié)果，嚴重時會影響運行穩(wěn)定性及造成疲勞破壞等，因此部分負荷工況下尾水管內(nèi)的壓力脈動特性研究受到學(xué)者持續(xù)關(guān)注[7-10]。

2000年，EUREKA(歐洲研究協(xié)調(diào)局)發(fā)起了FLINDT(Flow investigation in draft tube)研究項目[11]，旨在建立較大運行范圍的試驗數(shù)據(jù)庫進行CFD計算的比較和確認。文獻[12]對混流式轉(zhuǎn)輪出口渦旋流動進行了試驗和理論研究，以闡明尾水管壓力恢復(fù)系數(shù)出現(xiàn)突降的原因。文獻[13]用渦旋生成裝置模擬混流式水輪機在部分負荷下的運動，并對渦旋流動進行了LDA(激光多普勒測速儀)測試和數(shù)值模擬研究。數(shù)值計算分別采用DDES(延遲分離渦)-SA(Spalart-Allmaras)模型和RNGk-ε模型，結(jié)果表明兩種湍流模型預(yù)測的平均速度與試驗測試比較一致，而DDES-SA模型在最大與最小轉(zhuǎn)速工況的精度要更高。FLINDT項目的研究，有助于理解混流式水輪機彎肘型尾水管內(nèi)部流動特征及流動機理。

部分負荷工況下，模型試驗觀測到的螺旋形渦帶在尾水管內(nèi)同時具有軸向及周向運動，因此可將尾水管渦帶壓力或者速度脈動分解為同步分量和非同步分量，其中同步分量表示渦帶突進(PVR plunging)，非同步分量表示渦帶旋轉(zhuǎn)(PVR rotating)，分別表征渦帶在尾水管錐管段軸向及徑向的運動強度[14-15]，一些學(xué)者也對此進行了研究[16-18]。

由此可見，尾水管渦帶壓力脈動的同步及非同步分解，不僅有助于對渦帶運動過程直觀深入的理解，而且對于抑制以及改善部分負荷工況下尾水管渦帶的不利影響具有重要意義。然而，有關(guān)研究相對較少且僅進行了簡單的流動特征描述。基于此，本文以某混流式模型水輪機為研究對象，開展部分負荷工況下尾水管內(nèi)部流動特性的試驗測試和數(shù)值模擬研究，分析渦帶周期性演化過程及其誘導(dǎo)的壓力脈動特性，將時變壓力脈動進行同步及非同步分量的數(shù)學(xué)分解，對渦帶形成過程中同步及非同步運動分量的影響進行動力學(xué)分析，進一步理解尾水管渦帶的復(fù)雜流動特征及其動力學(xué)特性。

1 尾水管壓力脈動研究方法

1.1 流動控制方程及SST k-ω模型

非穩(wěn)態(tài)的雷諾時均(Reynolds average Navier-Stokes equations,RANS)方程為[19]

(1)

式中t——時間ρ——流體密度

p——壓力ν——渦粘度

xi、xj——笛卡爾坐標i、j方向位移

Ui、Uj——i、j方向上的時均速度

u′i、u′j——i、j方向上的脈動速度

采用SSTk-ω湍流模型來封閉式(1)，即

(2)

式中νt——湍動渦粘度

Sij——變形率張量

δijk——Kronecker算子

SSTk-ω湍流模型中湍動能及比耗散率的輸運方程為[20]

(3)

(4)

其中

式中k——湍動能ω——比耗散率

F1、F2——混合函數(shù)

Pk——湍動生成項

α、α1、β、β*、σk、σω、σω2——方程閉合系數(shù)

SSTk-ω湍流模型在邊界層使用k-ω湍流模型，在其余區(qū)域應(yīng)用k-ε湍流模型，可較好地捕捉葉輪機械的流動分離現(xiàn)象[21-23]。

1.2 計算域離散及邊界條件

本文研究對象為一轉(zhuǎn)輪直徑Dm=0.35 m的混流式模型水輪機，如圖1所示。該模型由進口到出口分別為蝸殼、活動導(dǎo)葉、固定導(dǎo)葉、轉(zhuǎn)輪以及尾水管，其中固定導(dǎo)葉與活動導(dǎo)葉數(shù)均為24，轉(zhuǎn)輪葉片數(shù)為15。額定工況下，活動導(dǎo)葉開度σ=24°，單位流量與單位轉(zhuǎn)速分別為Q11=0.933 0 m3/s，n11=73.43 r/min，對應(yīng)的原型水輪機水頭Hp=71.0 m，輸出功率PP=228.22 MW。

圖1 模型水輪機示意圖Fig.1 Sketch of investigated model Francis1.蝸殼 2.固定導(dǎo)葉 3.活動導(dǎo)葉 4.轉(zhuǎn)輪 5.尾水管

采用多塊結(jié)構(gòu)化六面體網(wǎng)格對蝸殼進口至尾水管出口計算域進行網(wǎng)格離散。為研究網(wǎng)格數(shù)目對計算結(jié)果的影響，采用美國機械工程師協(xié)會(American Society of Mechanical Engineers，ASME)推薦的網(wǎng)格收斂指數(shù)(GCI)[24-26]進行網(wǎng)格離散誤差的估計。GCI是一個具有95%置信區(qū)間、表示兩個對比網(wǎng)格中更密網(wǎng)格與漸進值之間距離的指標，可用于預(yù)測進一步的網(wǎng)格細化對求解的影響。GCI網(wǎng)格無關(guān)性驗證需要3套不同數(shù)目的網(wǎng)格，分別為細密網(wǎng)格(Fine)、中等網(wǎng)格(Medium)和粗糙網(wǎng)格(Coarse)，計算的近似相對誤差、外推相對誤差以及網(wǎng)格收斂指數(shù)公式為

(5)

式中ea、eext——近似相對誤差和外推相對誤差

φ——選擇的關(guān)鍵變量

φext——關(guān)鍵變量的外推值

r——網(wǎng)格加密因子

m——采用定點迭代法計算的表觀級數(shù)

下標1、2對應(yīng)于網(wǎng)格Fine和Medium，下標21為網(wǎng)格Fine對Medium的相對值。

網(wǎng)格Medium相對于Coarse的計算過程與式(5)相同。表1(N1～N3表示3種不同密度的網(wǎng)格數(shù)，下標3對應(yīng)于網(wǎng)格Coarse，下標32為網(wǎng)格Medium對Coarse的相對值)列出了最優(yōu)工況下數(shù)值計算離散誤差的計算過程及統(tǒng)計。數(shù)值計算蝸殼進口給定質(zhì)量流量，尾水管出口指定靜壓，固壁面均采用光滑、無滑移邊界條件。瞬態(tài)計算動靜交界面為“Transient rotor-stator”，對流采用高階求解格式，瞬態(tài)模型則采用二階向后歐拉模式，收斂標準設(shè)為最大殘差小于0.001。為消除變量之間代數(shù)運算帶來的誤差，選擇直接測得的兩個變量轉(zhuǎn)輪扭矩和活動導(dǎo)葉與轉(zhuǎn)輪之間無葉區(qū)測點的壓力作為網(wǎng)格無關(guān)性測試的關(guān)鍵變量。

表1 數(shù)值計算離散誤差及不確定性統(tǒng)計Tab.1 Statistics for discretization error and uncertainties in numerical solutions

由表1可知，3種密度的網(wǎng)格以漸進形式收斂，表明網(wǎng)格加密有利于平均流場的求解。對Fine和Medium網(wǎng)格而言，計算的扭矩不確定度分別為3.67%和5.69%，轉(zhuǎn)輪扭矩不確定度為0.92%和2.24%。為了平衡計算精度與計算資源之間的關(guān)系，本文最終選擇了Medium網(wǎng)格進行數(shù)值計算。圖2所示為蝸殼、固定導(dǎo)葉及活動導(dǎo)葉、轉(zhuǎn)輪和尾水管網(wǎng)格示意圖。其中蝸殼、固定導(dǎo)葉、活動導(dǎo)葉、轉(zhuǎn)輪及尾水管最大y+值(y+表示第1層網(wǎng)格距離壁面的無量綱距離)分別為135.6、60.8、50.2、56.2和58.6。

圖2 網(wǎng)格生成示意圖Fig.2 Grid views for simulation domain

1.3 數(shù)值計算方法的試驗驗證

數(shù)值計算與試驗測試工況為模型水輪機額定功率的42.35%，對應(yīng)的活動導(dǎo)葉開度σ=20°，單位轉(zhuǎn)速n11=88.00 r/min，單位流量Q11=0.745 2 m3/s。水輪機測試試驗臺如圖3a所示，試驗過程中采用電磁流量計記錄流量，壓差傳感器用來測量蝸殼進口與尾水管出口之間的壓差來計算水頭。為了捕捉尾水管渦帶壓力脈動，兩個徑向相差180°的微型壓力傳感器S201和S209被嵌入式安裝在尾水管錐管段壁面，以記錄時變壓力脈動的動態(tài)變化過程。模型試驗嚴格按照IEC60193試驗標準進行水力效率、流量的測量以及傳感器標定[27]。試驗前仔細檢查傳感器的精度和標定不確定度，流量計、壓差傳感器以及壓力傳感器的估計不確定度分別為±0.18%、±0.05%和±1%，模型試驗臺水力效率的隨機誤差與系統(tǒng)誤差分別為±1%和±0.214%。

除測點S201和S209外，數(shù)值計算額外監(jiān)測尾水管錐管段4個不同高度斷面上的壓力變化，如圖3b所示。4個斷面分別命名為S1、S2、S3和S4面，分別位于錐管段Z=-0.206 m、Z=-0.254 m、Z=-0.361 m和Z=-0.467 m，其中S2面為尾水管進口以下0.3D2(D2為轉(zhuǎn)輪出口直徑)處。在S2面上，錐管段壁面上逆時針間隔22.5°布置了16個測點，依次命名為S201～S216；錐管段內(nèi)部沿X方向分別布置7個測點，依次命名為S217～S223，其余3個平面按照相同的方法布置對應(yīng)的測點。

圖3 水輪機模型試驗臺及數(shù)值計算壓力測點位置Fig.3 Model test for Francis turbine and minoring point locations

統(tǒng)計得到尾水管渦帶壓力脈動幅值及主頻數(shù)值解與試驗測試的對比結(jié)果。其中，壓力脈動幅值采用線性計算，為壓力最大值與最小值之差的97%置信區(qū)間，頻率為快速傅里葉變換(FFT)獲得的主頻。試驗測得的幅值為11.398%，對應(yīng)的數(shù)值解為11.09%，計算誤差約為2.70%。試驗測試壓力信號經(jīng)FFT變換后的主頻為0.256fn(fn為轉(zhuǎn)頻)，為典型的尾水管渦帶壓力脈動頻率，數(shù)值預(yù)測的主頻為0.249 3fn，對應(yīng)的計算誤差為2.62%。對比結(jié)果可知，數(shù)值計算獲得的壓力脈動主頻及幅值與試驗值比較吻合，誤差在可接受范圍之內(nèi)，且在渦帶頻率上的預(yù)測精度略高于壓力脈動幅值。

2 結(jié)果分析

2.1 壓力脈動特性

圖4(圖中Cp表示壓力脈動系數(shù)，f表示頻率)為錐管段S2平面上沿X軸上5個測點S209、S217、S218、S219、S220的壓力變化曲線及對應(yīng)的FFT變換。圖5(圖中T表示尾水管渦帶運動周期)以S2面為例，給出了一個周期內(nèi)渦帶運動對平面壓力的影響示意圖，圖中同時給出了圖4中5個測點的位置分布。壓力脈動系數(shù)計算公式為

(6)

pBEP——最優(yōu)工況參考壓力

圖4 X軸測點時變壓力曲線及頻譜分析Fig.4 Temporal variation of numerical pressure coefficient and spectral analysis along X axis

圖5 進動渦帶對平面壓力的影響Fig.5 Influence of precessing vortex rope on pressure distribution

由圖4時變壓力及其FFT變換結(jié)果可知，轉(zhuǎn)輪旋轉(zhuǎn)10圈時間內(nèi)，尾水管內(nèi)壓力呈周期性低頻波動，F(xiàn)FT變換后各個測點上的主頻均為0.25fn，為典型的尾水管渦帶頻率。不同測點上壓力脈動幅值差異較大，幅值從大到小依次為S218、S217、S219、S209、S220。除轉(zhuǎn)軸中心測點S220外，造成其他測點幅值差異的原因，可以用圖5解釋。如圖5所示，部分負荷工況下橢圓形偏心渦帶的出現(xiàn)，對整個壓力場有直接影響。渦帶中心壓力最低，壓力由最低點向外部輻射增加，且渦帶所在一側(cè)壓力較低，對應(yīng)的另一側(cè)壓力較高，即當(dāng)渦帶掃過測點時，其壓力最低。因此，渦帶旋轉(zhuǎn)運動對壓力場帶來的影響表現(xiàn)為與渦帶中心距離越近，測點幅值越大。由圖5可知，S218位于渦帶運動軌跡上，其幅值最大；S217與S219位于渦帶兩側(cè)，其幅值小于S218，同理，壁面測點S209幅值小于S217和S219。對于測點S220，其位于轉(zhuǎn)軸中心，渦帶工況下錐管段中心一般為回流及死水區(qū)，故脈動幅值較小。

2.2 壓力脈動同步及非同步分解

尾水管錐管段內(nèi)的水流流動，同時具有周向旋轉(zhuǎn)運動和軸向豎直運動，為定量分析這兩種運動，可將尾水管內(nèi)的壓力信號分解為同步分量(Synchronous component)及非同步分量(Asynchronous component)[15,28-29]，公式為

(7)

(8)

式中Asyn、Aasyn——同步分量及非同步分量

A1、A2——尾水管錐管上關(guān)于水輪機軸對稱的壓力監(jiān)測信號

圖6 原始及分解后壓力信號Fig.6 Original and decomposed pressure signals

以測點S209與S201為例，圖6為壓力脈動系數(shù)以及分解后壓力脈動系數(shù)的同步分量、非同步分量隨時間變化曲線，圖7為同步與非同步分量壓力脈動系數(shù)頻譜分析結(jié)果。

圖7 同步及非同步分量壓力脈動頻譜分析Fig.7 Spectrum analysis of synchronous and asynchronous components

由圖6可知，兩個原始信號其脈動頻率及幅值均一致，僅在相位上有差別；分解后的壓力信號，非同步分量幅值絕對占優(yōu)，其壓力脈動幅值約為同步分量的2.51倍，并且非同步分量對原始信號具有依從性，即其主頻保持與原始信號一致，均為0.25fn，為低頻渦帶頻率，而由于原始信號波峰波谷間存在相位差，經(jīng)過壓力分解后的同步分量主頻發(fā)生變化，約為0.50fn。

為進一步量化錐管段不同高程上同步與非同步分量幅值，以及研究其沿軸向和周向運動的演化規(guī)律，圖8a給出了S2平面上壓力脈動幅值沿圓周方向的極軸分布圖，為圖3b中S2平面上S201至S216測點壓力脈動系數(shù)幅值沿圓周方向的擬合。該擬合曲線與等壓力脈動系數(shù)曲線呈偏心圓分布，定義極軸圖圓心與擬合圓圓心之間距離OO′為該平面上的壓力脈動系數(shù)的同步分量幅值，擬合圓半徑O′D為壓力脈動系數(shù)的非同步分量幅值。采用相同的處理方法，圖8b為錐管段4個不同高度截面上壓力脈動系數(shù)同步及非同步分量比較直方圖。

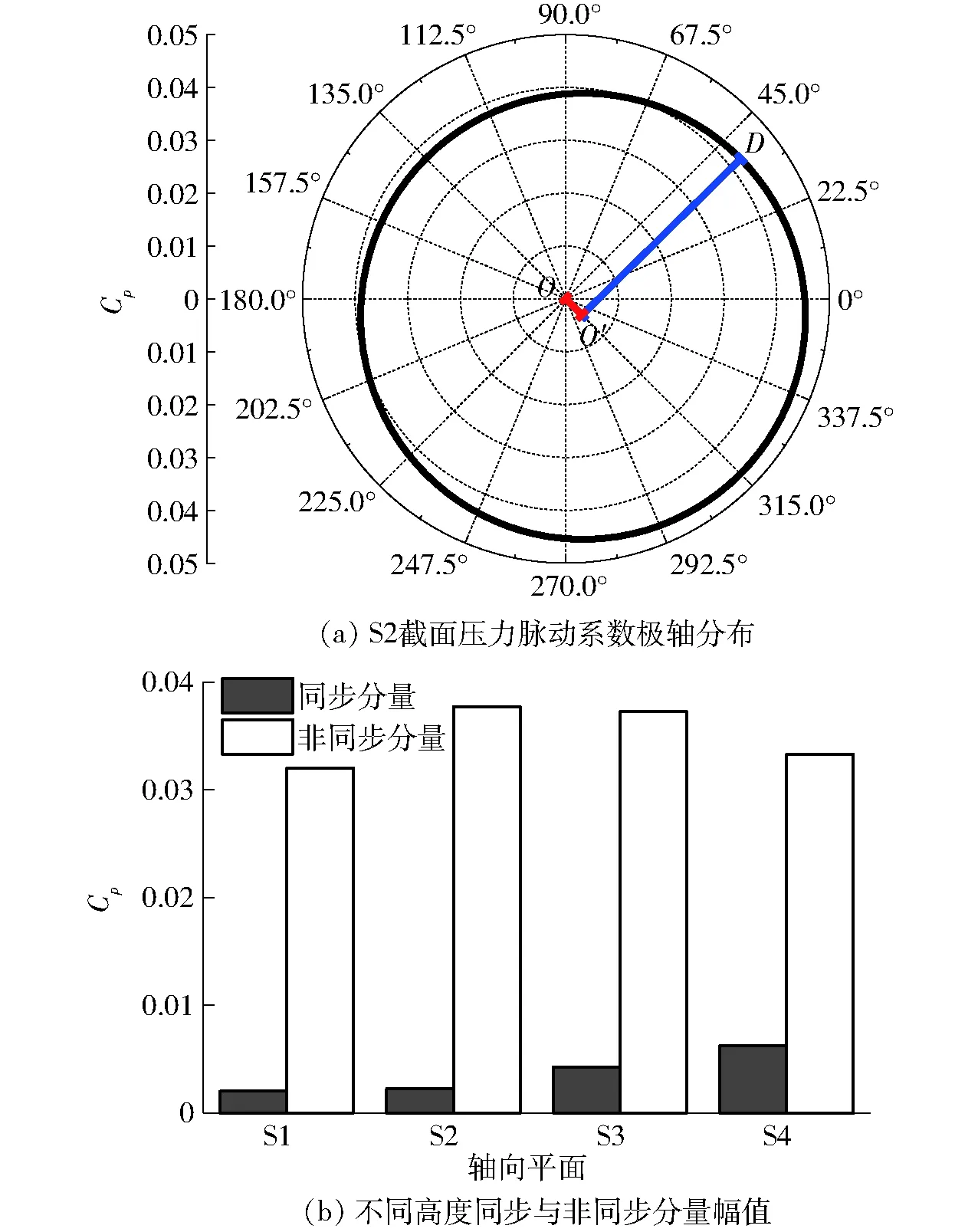
圖8 壓力脈動同步與非同步分量幅值比較Fig.8 Comparison of pressure amplitude of synchronous and asynchronous components

由圖8b比較分析可知，錐管段不同高度上非同步分量幅值均絕對占優(yōu)，同步分量與非同步分量之間的比值約為0.063、0.060、0.114、0.188，表明當(dāng)尾水管中出現(xiàn)螺旋形渦帶時，錐管段內(nèi)作螺旋狀渦旋運動的水流占主導(dǎo)作用。非同步分量由尾水管進口首先增大，在S2平面上達到最大值，然后減小，而表征壓力軸向運動的同步分量，其幅值沿流動方向逐漸增大。

3 結(jié)論

(1)研究了渦帶誘發(fā)的高幅值壓力脈動特性并對渦帶壓力脈動進行同步與非同步分量的數(shù)學(xué)分解。數(shù)值模擬與試驗測試均在42.35%額定功率下進行。數(shù)值仿真采用瞬態(tài)全通道計算，利用GCI技術(shù)進行網(wǎng)格無關(guān)性驗證并確定網(wǎng)格數(shù)目，最終獲得了與試驗測試壓力脈動主頻及幅值結(jié)果一致的數(shù)值解。

(2)尾水管內(nèi)出現(xiàn)進動渦帶時，錐管段內(nèi)不同測點均呈低頻周期性脈動，預(yù)測的脈動主頻為0.25fn，為典型的尾水管渦帶頻率。由于渦帶中心為低壓區(qū)，渦帶所在一側(cè)壓力較低，對應(yīng)的另一側(cè)壓力較高，故距離渦帶運動軌跡越近的位置，其壓力變幅越大，導(dǎo)致壓力脈動幅值高于周圍位置。

(3)將渦帶壓力脈動分解為同步分量與非同步分量，分解后的壓力信號，非同步分量壓力脈動幅值較高，且保持了與原始信號一致的0.25fn主頻。同步分量主要受原始信號波峰波谷間相位差的影響，其主頻發(fā)生變化。沿流動方向非同步分量壓力脈動幅值首先增大，然后減小，而表征壓力軸向運動的同步分量，其幅值逐漸增大。