基于綜合指標的機床滾珠絲杠進給系統動態性能優化

楊 勇 孫 群 朱其新 陳 盛

(1.蘇州科技大學機械工程學院, 蘇州 215009； 2.蘇州科技大學蘇州市精密與高效加工技術重點實驗室, 蘇州 215009；3.上海電機學院機械工程學院, 上海 201306； 4.南京郵電大學自動化學院， 南京 210023)

0 引言

機床滾珠絲杠進給驅動系統[1]作為一個典型的機電耦合系統，其伺服控制輸出的力直接作用于機械傳動環節，而機械傳動環節的位移、速度、加速度一方面會影響機械系統的運動特性，另一方面其作為反饋信息反饋至伺服控制會影響伺服控制及整個滾珠絲杠進給驅動系統的運動響應性能[2-3]，受進給驅動系統機械結構振動的影響，需降低位置環增益以確保整個進給系統的穩定性。為分析整體滾珠絲杠進給驅動系統的運動響應特性[4-5]，需要對該系統集成建模，以往研究學者在集成建模時多采用在不同仿真環境下分別對機械和控制子系統建模，通過軟件接口的信息交互實現機械傳動與伺服控制耦合集成模型，但受限于軟件接口的兼容性、擴展性，集成模型精度和效率會受到影響[6-7]。

在對滾珠絲杠進給驅動系統運動響應特性進行評價時，可以選用超調量、調節時間、上升時間、穩態誤差等響應特征[8-10]，但這些響應特征僅能表征某項品質指標，且因其數量級差異較大難以采用多目標優化方法實現運行響應性能的綜合評價[7]。

為此，眾多研究中引入系統理想輸出和實際輸出之間的誤差函數評價系統的運動響應性能，如平方誤差積分函數ISE、時間乘平方誤差積分函數ITSE等。相較于前述響應特性評價指標，該誤差函數在一定程度上實現了對系統綜合響應性能的表征，但不同的誤差積分準則函數同樣側重于不同的運動響應性能表征，如時間乘絕對誤差積分準則函數ITAE雖然能確保系統瞬態響應振蕩較小，但很難保證幅值穩定裕度；而平方誤差積分準備函數ISE具有較快的響應速度但是振蕩性較大，穩定性較差。可以看出，這些誤差函數仍相對側重于運動響應的某些特征指標，仍然無法根據優化需求綜合評價系統運動響應性能，且當選取某一誤差積分函數作為優化目標函數時，無法根據優化需求對系統性能及伺服參數進行實時調節。

本文建立滾珠絲杠進給系統理論動力學模型并對其響應傳函特性進行分析，并構建基于數字化模塊仿真的滾珠絲杠進給驅動系統集成模型，通過狀態空間表示法在同一仿真環境下建立并集成機械結構與伺服控制子模塊模型。提出基于擴縮式伺服控制優化模型的滾珠絲杠進給驅動動態性能優化方法，建立滾珠絲杠進給系統可擴縮式伺服控制優化模型，構建面向綜合指標評價的可擴縮式動態性能指標評價函數，根據動態性能優化要求實時建立動態性能綜合評價指標函數，通過運動路徑規劃定義，借助遺傳優化算法，實現面向可擴縮式綜合指標評價的滾珠絲杠進給驅動系統動態性能優化。

1 滾珠絲杠進給系統理論動力學建模與分析

滾珠絲杠進給系統示意圖見圖1a，其包含電機、聯軸器、絲杠、螺母、導軌、工作臺等，聯軸器將電機的往復旋轉運動傳遞至絲杠，絲杠螺母副將絲杠的往復旋轉運動轉換為螺母的往復直線運動，螺母與工作臺之間的固定聯接使螺母帶動工作臺沿著導軌往復運行。

圖1 滾珠絲杠進給系統理論動力學簡化模型Fig.1 Simplified modeling of theoretical dynamics for ball screw feeding system1、7.電機 2.聯軸器 3.導軌 4.工作臺 5.螺母 6.絲杠 8.等效負載

滾珠絲杠進給系統動力學理論簡化模型如圖1b所示，其將電機作為動力件，其轉動慣量為Jm，由電機帶動的聯軸器、絲杠、螺母、工作臺作為負載，設其等效負載轉動慣量為Je，電機輸出力矩為M，電機和等效負載之間存在等效剛度k和等效阻尼系數c。以聯軸器作為等效構件，選取聯軸器角速度ωc為等效構件角速度ωe，根據等效前后能量守恒定理可得

(1)

式中Jc、Js——聯軸器和絲杠的轉動慣量

mn、mt——螺母和工作臺質量

ωs——絲杠角速度

vn、vt——螺母和工作臺的移動速度

根據式(1)可得

(2)

根據各運動變量之間的關系，拉氏變換為

(3)

式中φm、φe——電機與等效負載的角位移

ωm——電機角速度

αm、αe——電機與等效負載的角加速度

對電機與等效負載分別進行受力分析，可建立其動力學基本方程并進行拉氏變換得到

(4)

將式(3)代入式(4)可得

(5)

基于自動控制原理，可分別得到式(3)、(4)的信號流圖，并最終綜合為整體信號流圖如圖2所示，可以看出其物理變量之間存在相互耦合關系。基于梅森增益公式，求解M(s)與φm(s)之間的傳遞函數為

(6)

其中Δ=1-∑La+∑LbLc-∑LdLeLf+…

式中 ∑La——所有單獨回路增益之和

∑LbLc——兩兩不接觸回路增益乘積之和

∑LdLeLf——每3個互不接觸回路增益乘積之和

pk——第k條前向通路總增益

Δk——流圖余因子式，其等于去掉與第k條前向通路接觸的回路后的流圖特征式

分析可得

(7)

圖2 滾珠絲杠進給系統理論動力學模型信號傳遞流程圖Fig.2 Signal transfer flow chart of theoretical dynamic model of ball screw feed system

將式(7)代入式(6)最終化簡可得

(8)

從式(8)可以看出，其分子是典型二階系統傳遞函數的標準形式，依據二階系統無阻尼自然頻率ωn以及阻尼比ζ公式可知

(9)

(10)

將式(8)分子分母同除以Je，并將式(9)、(10)代入式(8)可得

(11)

在上述基礎上進一步求解φm(s)和φe(s)之間的傳遞函數P2。令M等于0并且去掉其關聯部分，將φm(s)作為輸入，對圖2進行簡化可得φm(s)和φe(s)之間的傳遞函數框圖如圖3所示，同樣采用梅森增益公式求解其傳遞函數可得

(12)

將式(9)、(10)代入式(12)，最終可得

(13)

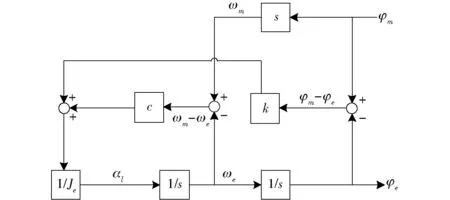
圖3 電機轉角到等效負載轉角的傳遞函數框圖Fig.3 Transfer function diagram of motor rotation angle to equivalent load rotation angle

由式(12)可以看出，其分母為典型的二階傳遞環節，而其分子為典型的一階延遲傳遞環節，其綜合作用的結果是幅值響應曲線在系統固有振動頻率處下降。因此可知，其系統固有頻率對伺服控制回路中的實際位置及位置環增益參數產生重要的影響，只有在低于該振動頻率的控制帶寬內，控制信號才能無衰減無延遲傳遞。

此外，可以看出，力矩與電機輸出轉角之間的傳遞函數P1、電機轉角與負載轉角之間的傳遞函數P2的零極點發生顛倒，傳遞函數P2的極點即為傳遞函數P1的零點，因此根據其零極點對應關系，在通過頻響函數P1測試確定系統固有頻率時，亦可以通過頻響函數P2的零極點測試確定系統固有頻率。

2 基于數字化模塊仿真的滾珠絲杠進給驅動系統集成建模

根據數字化模塊仿真方法，將滾珠絲杠進給驅動系統分為伺服控制子模塊和機械傳動子模塊，進一步通過狀態空間表示法[11-12]在同一仿真環境下建立并集成機械結構與伺服控制子模塊模型，整體流程示意圖見圖4。

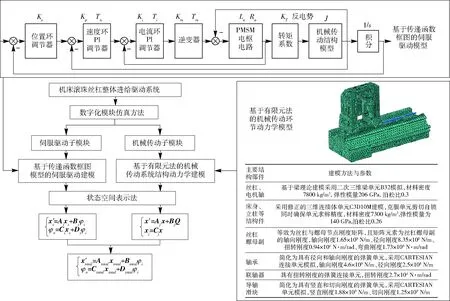
圖4 基于數字化模塊仿真的整體滾珠絲杠進給驅動系統建模示意圖Fig.4 Modeling schematic of whole ball screw feed drive system based on digital module simulation

狀態空間表示法是通過含狀態變量的微分方程組建立系統內部狀態變量與外部輸入變量和輸出變量間的關系。通過系統的動力學微分方程或系統的傳遞函數/傳遞函數框圖均可建立基于狀態空間表示法的系統模型。通常采用傳遞函數/傳遞函數框圖對伺服控制系統進行建模，而常采用動力學微分方程對機械系統進行結構動力學建模。故狀態空間表示法可很方便實現同一仿真環境下的機械傳動與伺服控制的數字化模塊建模集成。

實際機床滾珠絲杠伺服驅動系統常采用經典級聯式控制，作者在文獻[13]中已建立了基于傳遞函數框圖的滾珠絲杠進給系統級聯伺服控制模型，見圖4中基于傳遞函數框圖的伺服驅動模型。經計算，滾珠絲杠進給驅動位置環傳遞函數G(s)可以簡化為

(14)

式中φi(s)——滾珠絲杠進給系統伺服控制的理想輸入位置

φo(s)——滾珠絲杠進給系統伺服控制的實際輸出位置

b0、b1、…、bn——滾珠絲杠伺服控制傳遞函數的分子系數

a0、a1、…、an——滾珠絲杠伺服控制傳遞函數的分母系數

采用長除法，將式(14)轉換為

(15)

其中

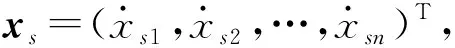
設E為單位矩陣，將上述各式寫作矩陣形式為

(16)

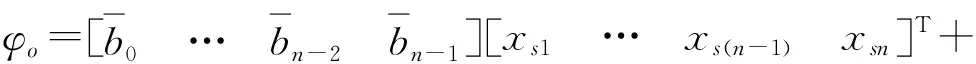
(17)

令

代入式(16)、(17)可得滾珠絲杠伺服控制狀態空間表達式為

(18)

滾珠絲杠機械傳動環節的輸入輸出量分別為電機扭矩與機械結構位移矢量，基于有限元的滾珠絲杠機械結構模型(圖4)的結構動力學方程為

(19)

式中Mj、Cj、Kj——滾珠絲杠機械結構的質量、阻尼、剛度矩陣

xj——滾珠絲杠機械結構位移矢量

Q——電機輸出扭矩，其為滾珠絲杠機械傳動環節的輸入力

根據狀態空間表示法，可得滾珠絲杠機械傳動環節狀態空間表達[13]為

(20)

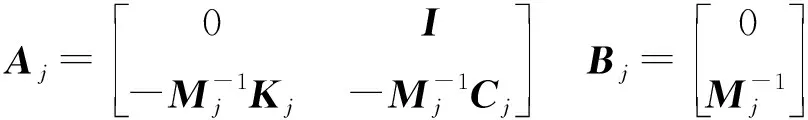
需要注意的是：在構建上述滾珠絲杠伺服控制狀態空間表達時，將滾珠絲杠機械傳動環節簡化為等效轉動慣量J的剛體來表達輸入Q與輸出xj之間的關系，而實際基于該滾珠絲杠機械傳動環節狀態空間表達的輸入Q與輸出xj間關系，同樣可得到如式(16)、(17)的基于狀態空間表示法的滾珠絲杠進給驅動整體標準式。

滾珠絲杠機械傳動環節結構部件的建模方法及具體參數見圖4，此外在實際建模過程中滾珠絲杠伺服控制系統的相關參數為位置環增益Kv=25 s-1，速度環增益Kp=27.3 N·m·s/rad，速度環積分時間Tn=60 ms，電流環增益Ki=12.157 V/A，電流環積分時間Ti=2 ms，電感系數La=3.1 mH，電阻系數Ra=0.075 Ω，反電勢系數Ke=1.67 V·s/rad，扭矩系數KT=2.72 N·m/A。

3 基于擴縮式伺服控制優化模型的滾珠絲杠進給驅動動態性能優化

提出基于擴縮式伺服控制優化模型的滾珠絲杠進給驅動動態性能優化方法，建立滾珠絲杠進給系統可擴縮式伺服控制優化模型，構建面向綜合指標評價的可擴縮式動態性能指標評價函數，根據動態性能優化要求實時建立動態性能綜合評價指標函數，通過運動路徑規劃定義，借助遺傳優化算法，實現面向可擴縮式綜合指標評價的滾珠絲杠進給驅動系統動態性能優化。

3.1 擴縮式伺服控制優化模型構建

3.1.1路徑運動規劃數學建模

為保證數控機床伺服運動的可靠性，避免起停運動的沖擊、失步、超程等，在同樣的起點終點位置(直線)間，數控系統可以采用不同加減速控制算法實現不同的路徑運動規劃，傳統數控系統中常用的加減速算法有直線型加減速和指數型加減速。這兩種方式在啟動和結束時均存在加速度突變，容易產生沖擊，因此不適用于高速高精度數控系統。通常高速高精度數控系統加減速路徑規劃可以分為兩類：插補前加減速控制和插補后加減速控制。實際加工過程中常采用指數型控制算法作為插補前控制，而采用鐘型加減速控制算法(加減速算法在加減速階段不存在加速度突變的現象)或者多次項加減速算法(加加速度無突變現象)作為插補后控制[14-15]。

為了降低其伺服跟隨延遲應盡量使各軸位置環增益相同，在保持系統穩定的前提下位置環增益盡量取大值，同時可以選擇較好的加減速控制方式降低加減速延遲軌跡誤差。根據現代機床的高速高精度特點，并且考慮到實際加工，選取插補后多項式加減速控制算法作為擴縮式伺服控制優化模型的路徑運動規劃以降低加減速延遲軌跡誤差，此時伺服跟隨誤差對加工誤差的影響性更為突出，其可通過選擇合適的控制參數來降低誤差。

通過函數疊加法，建立該伺服控制優化模型的多項式加減速控制算法的加加速度的數學式

(21)

(22)

式中jmax——最大加加速度設定值

hi——heaviside分段函數

將式(21)中的加加速度路徑規劃定義式進行拉氏變換，可得

(23)

式中L——拉氏變換計算

加加速度j、加速度a、速度v、位移q之間的關系為

(24)

式中L-1——拉氏逆變換計算

對式(24)進行拉氏變換與拉氏逆變換，最終可得該伺服控制優化模型的路徑運動規劃加加速度、加速度、速度、位移曲線如圖5所示。

圖5 滾珠絲杠進給系統伺服控制優化模型的路徑規劃曲線Fig.5 Path planning curves of servo control optimization model for ball screw feed system

在實際路徑規劃定義時，文獻[16]采用C++語言S函數方法實現路徑規劃定義，而本文采用Matlab中的sim函數定義滾珠絲杠進給系統伺服控制優化模型路徑規劃。

3.1.2優化變量選取

通常伺服控制系統采用級聯控制對位置環、速度環以及電流環的增益及積分時間進行優化，但是由于電流環控制參數可以通過電機生產商取得，并且不需要通過復雜的伺服仿真模型便可以進行調整，因此，本文選取速度環增益、積分時間、位置環增益3個參數進作為優化變量。

3.1.3評價函數

根據動態性能優化要求實時建立滾珠絲杠進給系統動態性能綜合評價指標函數，將上述動態響應誤差函數等定義為系統性能指標(System performance index, SPI)，基于二次型評價指標原理，構建滾珠絲杠進給系統響應特性的的擴縮式目標評價函數(Scalable objective evaluation function, SOEF)數學表達式為

(25)

式中n——系統性能評價指標數量

wi——單個性能指標在整體評價函數中所占的權重

從式(25)可以看出，如果權重系數wi置為0，則對應的性能指標不會對整體評價函數產生任何影響，而如果該權重系數增加，則其對整體評價函數的貢獻增大，反之亦然。因此，可以通過該權重函數的選擇實現滾珠絲杠進給系統動態性能評價指標的可擴縮性及系統動態性能評價指標配重調整。

從式(25)可以看出，指標評價函數具有確定的函數形式，具有可擴縮性。根據動態性能優化需求，可方便地對動態性能指標評價函數進行調整，動態性能優化需求不同時，無需重新構造指標評價函數，無需重新設置動態性能不同評價指標之間權重函數，指標評價函數構造可更加快速與便于調整。

滾珠絲杠進給系統性能指標SPI可以選用對響應特征值綜合處理的理想輸出和實際輸出之間的標準誤差積分函數如ISE、ITSE等，亦可以根據需求自定義滾珠絲杠進給系統性能指標SPI，如本文后續優化時則采用式(26)所示的自定義SPI函數反映滾珠絲杠進給系統動態響應的超調與暫態震蕩。

(26)

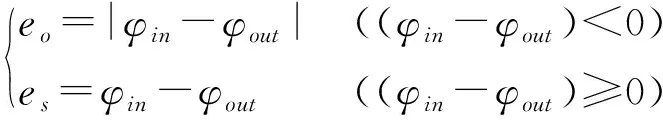
式中fo、fs——以時間為變量的超調與暫態震蕩的加權系數

3.1.4優化算法確定

在前述路徑運動規劃數學建模、面向綜合指標評價的可擴縮式動態性能指標評價函數構建、優化變量選取等的基礎上，進一步選擇滾珠絲杠進給驅動動態性能優化過程中的智能優化算法。基于遺傳優化算法的自適應全局優化搜索特點，選取遺傳優化算法進行面向綜合指標評價的滾珠絲杠進給驅動動態性能優化。

3.2 結果與分析

采用西門子840D型數控系統[17-18]機床，通過西門子840D系統內置的面板控制單元PCU50，以及相應的集成于操作界面軟件HMI Advanced上的測試工具Start-up tool(IBN-Tool)[17-20]，可以實現機床滾珠絲杠進給驅動系統動態性能頻率響應測試，其頻響測試信號來源于機床滾珠絲杠進給驅動系統內置的電機編碼器、霍爾電流傳感器等內置傳感器。

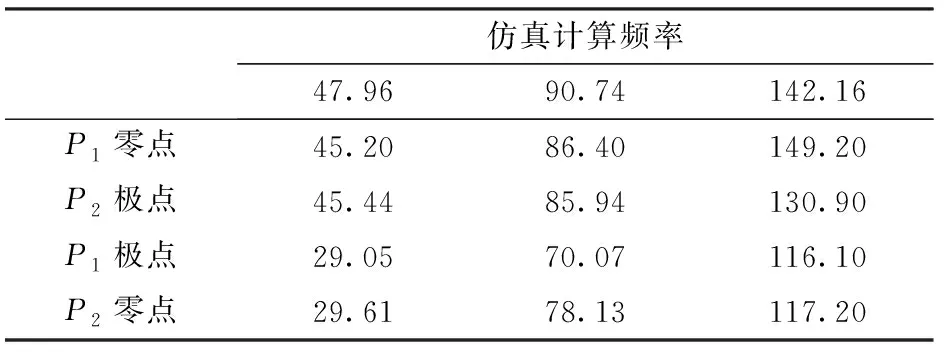
基于該機床滾珠絲杠進給驅動系統內置傳感器型號，借助面板控制單元PCU50和頻響測試工具Start-up tool(IBN-Tool)，得到的滾珠絲杠進給驅動系統電機轉角與負載轉角間頻響P1、電機轉角與負載轉角之間的傳遞函數P2如圖6所示。滾珠絲杠進給系統仿真計算頻率、P1頻響(零極點)、P2頻響(零極點)的對應關系見表1。

圖6 P1(電機轉角與負載轉角間頻響)與P2(電機轉速與力矩間頻響)的零極點對應關系Fig.6 Aero-pole correspondence relationship between P1 (frequency response between motor rotation angle and load rotation angle) and P2(frequency response between motor speed and torque)

Hz

綜合圖6與表1可以看出，力矩與電機輸出轉角之間頻響函數P2、電機轉角與負載轉角之間頻響函數P1的零極點發生顛倒，這與前述滾珠絲杠進給系統理論動力學建模分析結論相符；力矩與電機輸出轉角之間頻響P2的零點(29.61、78.13、117.20 Hz)即為電機轉角與負載轉角之間頻響P1的極點(29.05、70.07、116.10 Hz)；電機轉角與負載轉角之間頻響P1的零點即為力矩與電機輸出轉角之間頻響P2的極點，且P2極點(45.44、85.94、130.90 Hz)、P1零點(45.20、86.40、149.20 Hz)與滾珠絲杠進給驅動系統仿真計算頻率(47.96、90.74、142.16 Hz)誤差較小。由圖6可知，在第1個極點位置即一階固有頻率處，幅值響應計算值(35.16 dB)與測試值(32.83 dB)相差較小，從圖6也可以看出，滾珠絲杠進給系統仿真計算曲線與實測曲線吻合度較好。綜上分析，說明所構建的滾珠絲杠進給系統理論動力學建模與分析結論的正確性，驗證了基于數字化模塊仿真的滾珠絲杠進給驅動系統集成模型的正確性。

在此基礎上，根據前述基于擴縮式伺服控制優化模型的滾珠絲杠進給驅動動態性能優化方法，借助前述滾珠絲杠進給系統可擴縮式伺服控制優化模型，采用不同的優化情形實例，根據動態性能優化要求實時建立動態性能可擴縮式綜合評價指標函數，實現面向可擴縮式綜合指標評價的滾珠絲杠進給驅動系統動態性能優化。

優化情形1：當選取滾珠絲杠進給系統理想輸出和實際輸出間平方誤差積分為滾珠絲杠進給系統性能指標SPI1時，即SPI1=ISE，根據可擴縮式目標評價函數得到的滾珠絲杠進給系統動態響應SOEF數學式為SOEF=SPI1。此時更強調滾珠絲杠進給系統的快速響應特性而對系統振蕩關注較少，優化后得到的動態響應曲線見圖7中優化曲線1，可以看出相比于優化前階躍響應曲線(上升時間與調節時間均為0.152 s)，該曲線響應速度較快(上升時間0.034 s)，調節時間相對較短(0.084 s)，但有略微超調且動態響應的穩定性較差。這些與ISE誤差積分函數動態響應評價特性優化需求相吻合。

圖7 不同優化情形下的滾珠絲杠進給驅動系統動態響應優化結果Fig.7 Dynamic response optimization results of ball screw feed drive system under different optimization conditions

優化情形2：在前述基礎上，基于面向綜合指標評價的可擴縮式動態性能指標評價函數，若更加注重滾珠絲杠進給系統的穩定性需求，即系統在高速運行時動態響應穩定，進一步選取滾珠絲杠進給系統理想輸出和實際輸出間時間乘絕對誤差積分ITAE為滾珠絲杠進給系統性能指標SPI2，且指定SPI2具有相對較大的權重系數，即w1=1，w2=2，且f1=1，f2=2，根據可擴縮式目標評價函數最終得到的滾珠絲杠進給系統動態響應SOEF數學式為SOEF=(f1(SPI1)f2(SPI2)2)1/3。優化后得到的動態響應曲線見圖7中優化曲線2，分析可得，相比于前一動態響應評價特性優化需求，該動態響應穩定性很好，雖響應速度(上升時間0.050 s)略微降低，但無超調現象出現，且調節時間(與上升時間相同均為0.050 s)很短，與其預設的動態性能優化需求一致。

綜上可以看出，通過該基于擴縮式伺服控制優化模型的滾珠絲杠進給驅動動態性能優化方法，根據動態性能優化要求采用不同的優化情形實例建立動態性能可擴縮式綜合評價指標函數，得到的面向綜合指標評價的滾珠絲杠進給驅動系統動態性能優化結果，與預設的動態性能優化需求一致，也說明該基于擴縮式伺服控制優化模型的滾珠絲杠進給驅動動態性能優化方法的正確性。

4 結論

(1)建立了滾珠絲杠進給系統理論動力學模型并對其響應傳函特性等進行分析，構建了基于數字化模塊仿真的滾珠絲杠進給驅動系統集成模型。

(2)提出了基于擴縮式控制優化模型的滾珠絲杠進給驅動動態性能優化方法，構建了面向綜合指標評價的可擴縮式動態性能指標評價函數，根據動態性能優化要求實時建立動態性能綜合評價指標函數，通過運動路徑規劃與定義，借助遺傳優化算法，實現了面向可擴縮式綜合指標評價的滾珠絲杠進給驅動系統動態性能優化。

(3) 通過實驗測試與實例分析，驗證了前述滾珠絲杠進給系統理論動力學建模與分析結論、基于數字化模塊仿真的滾珠絲杠進給驅動系統集成模型、基于擴縮式控制優化模型的滾珠絲杠進給驅動動態性能優化方法的正確性。