磁場中的能量守恒問題

蘇鈺堯

（徐州市第一中學，徐州 221006）

電磁場，是真實的存在于人類所生存的空間之中，且還會攜帶一部分相對特殊具備電磁性質的一類物質。在電磁場之中的能量守恒問題，則是熟悉并學習電磁場理論的根本基礎，在電磁場之中能量守恒定律的條件主要就是各類能量相互之間實施轉換而來，從而在電磁場的內部予以成型。

1 利用能量守恒定律來判斷感應電流的方向

如何將感應電流的方向判斷出來，這是高中物理電磁場學習過程之中經常會碰到的題型，但是依據楞次定律得知，感應電流都是有方向的，其實質上就是感應電流的磁場勢必會影響到引起感應電流的磁通量所發(fā)生的變化。那么不僅僅是運用楞次定律來判斷感應電流，也可以利用能量守恒定律來予以判斷。

我們主要從磁通量層面來進行分析，閉合線圈主要就是因為磁通量發(fā)生改變而出現的感應電流和感應電動勢。另外從能量的層面來進行分析，磁鐵在下落的階段之中必須要抵抗線圈的磁場力來予以做功，并實施電能與機械能之間的轉換，所以在線圈之中出現感應電流后，其上端的磁鐵勢必就是臨近一端的同名極，相應的就會和磁鐵之間出現排斥的情況。據此隨即就可以推斷出來，線圈之中，S 極為下端，N 極為上端，再依照安倍定律來判斷感應電流的具體方向。

2 實例證明

分析電磁場能量守恒規(guī)律，這是一項十分繁雜、很難理解的過程，那么為了確保可以更加的生動化與直觀化，在具體分析電磁場能量守恒規(guī)律之前來參照一個實例，從而就可以更好的理解到電磁場能量守恒規(guī)律。

物理實例條件：一個表面帶點且質量均化的球殼，該球半徑設定為r，假如球殼表面所分布的電量均勻，電量是q，從條件之中我們隨即可以提出兩個值得思考的問題：首先是進行設置，促使該帶點球在空間之中實施均勻化的旋轉，且運用垂直軸線來進行參考，將其轉動的速度基本上設定為ω，求該點球殼內部電磁場電量的分布情況；其次假使設定在具體某一個時刻，那么在外力矩作用的標準之下，帶電的球運用α=Δω/Δt 的角加速度在垂直中軸實施移動，著重分析在該類速度之下外力所出現的力矩（外力矩）m 和功率p 數值的具體數值。

依據以上的物理實例得知，帶點球質量均勻，表面之上所攜帶電荷在球殼之內的分布相對均勻，在經過一系列的實驗之后，球殼之上的電四極矩與電偶極矩的矩數都是零，因此在實驗之中并不會出現電偶極與電四級的影響，相應的這也就等同于該實驗出現是在為出現電偶極與電四級輻射的標準之下來實施。

3 能量守恒

3.1 無外力作用時的電磁場能量守恒

在沒有外力作用的情況之下，相應區(qū)域V 之內的帶電體能量改革率是：

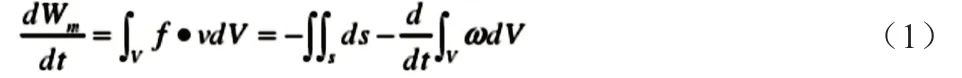
公式（1）中Wm代表的是區(qū)域V 之中帶電體的機械能量；f=ρ（E+v×B）則表達的是洛倫茲力的密度；f·v 代表的是f 的功率密度；∫vf·vdV 代表的是該區(qū)域內f 的總功率；s=E×H 代表的是能量流密度；w=1/2（E·D+B·H）代表的是電磁場之中的能量密度。另外公式（1）的物理意義實質上就是：在區(qū)域之內機械能量與電磁能量的增加率。

3.2 有外力作用下的電磁能量守恒

在出現外力FW（功率為PW）作用的情況之下，公式（1）隨即就可以改寫成以下的形式：

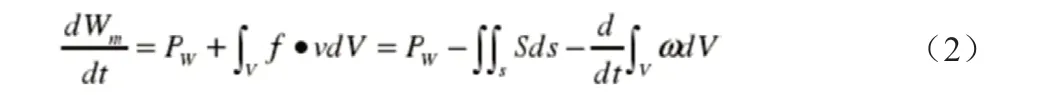
3.3 電磁場能量守恒的實例分析

假設公式（2）之中S 曲面是一個無窮大的區(qū)域，同時也就是全空間；在以上實例之中，s=E×H，隨即可以得知，在該無窮大的范圍之中的能量密度是零，隨即可以就可以針對公式（2）予以推算，

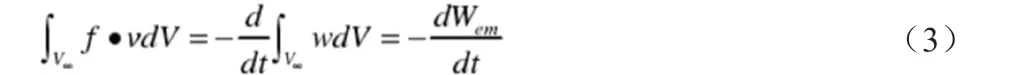
由上得知，在空間磁場之中一個固定曲面之中所通過的能量流密度通量是零的情況之下，那么帶電體在該空間磁場之中相應的就會受到電磁力矩在其中具體發(fā)生電磁功率的情況來予以決定。

在以上的物理實例之中，帶電體受到電磁力矩的影響，會直接性的阻礙到球殼出現轉動，在這種形勢之下，球殼受到電磁場能量，從而在加大外力矩作用情況之下，相應的表達機械功率的公式如下：

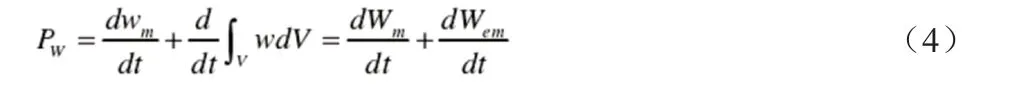
依據以上公式得知，在空間電磁場之中，處在一個能量流密度是零的曲面之上，在受到外部力的影響之下，那么加大電磁功率也就是在外力情況之下所出現的機械功率。運用公式推導就可以推算出公式（5）：

依據以上結果和上一節(jié)之中，運用電磁場角動量守恒公式而推算出來的結果相同。

4 結束語

總之，目前針對電磁場之中的能量守恒問題，分析闡明坡印廷理論，所得到的結論就是傳輸線不會出現電路能量損耗情況。最終在通過以上的分析研究之后，可以得到電路能耗關系和電磁之間的關系，從而也就進一步的驗證了在傳輸過程之中電路系統能量守恒，進而為電磁場能量守恒的方面的研究提供了堅實的基礎。由此可見，本文的研究也就顯得十分的有意義。