STATCOM自適應分數階重復控制的研究
王素娥, 燕晨陽, 郝鵬飛
(陜西科技大學 電氣與信息工程學院,西安 710021)
0 引 言
分布式發電、大型軋鋼機、電力機車等負荷的運行產生了低次諧波,嚴重影響設備正常使用。靜止同步補償器(STATCOM)是交流柔性輸電的核心裝置之一,通過向電網注入補償電流抵消負載產生的無功與諧波,具有調節速度快、成本低、體積小等優點,已經越來越多地應用于風電場和光伏電站[1-4]。
三相電壓型STATCOM的控制方法中,傳統PI控制簡單易實現,但抑制諧波的能力較差,對指令補償電流跟蹤精度較低[5]。諧振控制器理論上在諧振頻率處具有無窮大增益,在諧振頻率處可以實現對信號的無靜差跟蹤。文獻[6]中采用多重比例諧振控制器并聯控制方式,有效抑制了電網的各次諧波,但多重諧振項參數設計復雜。重復控制在基波頻率及諧波頻率處都產生較高的增益,可以視為多個諧振控制器并聯的形式,進而對諧波具有好的抑制效果[7]。
國標規定電力系統正常運行時頻率會存在(±0.2~±0.5) Hz偏差,在電力系統不正常運行時偏差則達到±1 Hz,而且基波的頻率偏差會在諧波頻率處成倍放大。當電網頻率波動時,控制器諧振頻率會偏離實際電網頻率,導致其增益下降,補償精度降低。文獻[8-9]中通過實時改變數字系統采樣頻率保證重復控制器內模環節的相位滯后階數與電網頻率的整數倍關系,而采樣頻率的不斷變化必然會使控制器設計復雜化;文獻[10]中引入內模系數Q將重復控制各諧振點變為準諧振,增加了控制器對電網頻率的適應能力,但算法受準諧振控制器的帶寬限制,無法在頻率波動較大時保持控制精度。
本文針對傳統重復控制器對電網頻率波動適應性差的問題,采用一種自適應分數階重復控制策略。使用基于拉格朗日插值多項式的線性近似方法實現重復控制內模的分數階滯后環節,根據鎖相環得到的實時電網頻率,在線計算內模參數,使控制器諧振頻率動態跟蹤電網頻率變化,提高靜止同步補償器的補償性能。通過仿真,證明所提方案的有效性與可行性。
1 系統原理與結構
圖1是STATCOM單相等效電路,圖中:L、R為交流側電感、線路等效電阻;C為直流側電容;us、uab、is分別為交流電壓、變流器輸出電壓、變流器輸出電流。
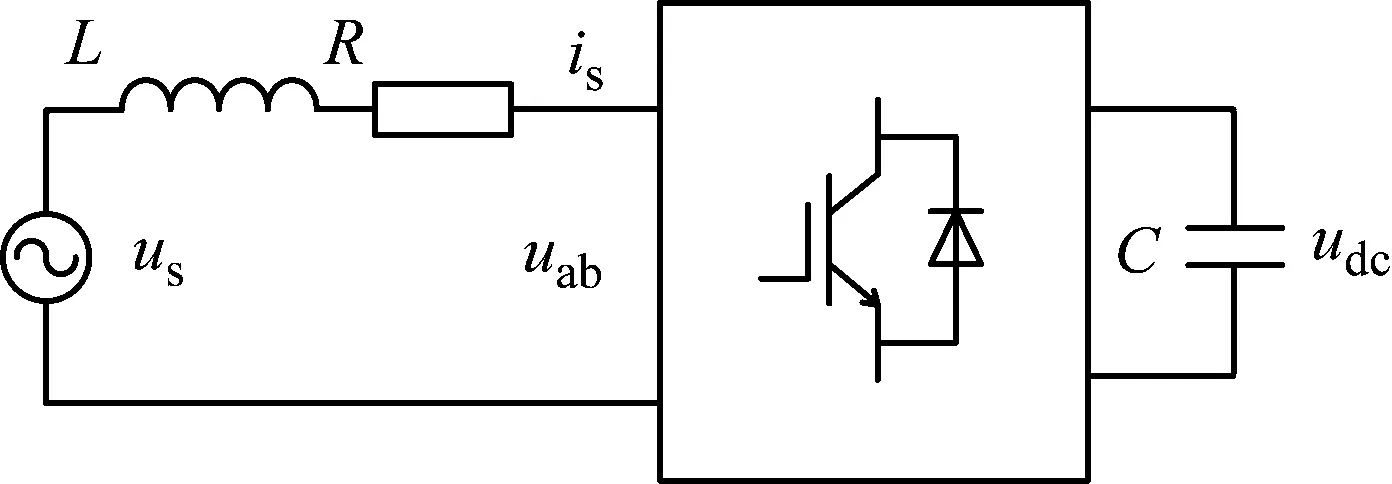
圖1 STATCOM單相等效電路
根據KVL定理,可得:
(1)
對式(1)拉氏變換,可得STATCOM的數學模型:
(2)
可知,在交流電壓us一定的情況下,通過相應算法控制變流器輸出電壓uab,即可以產生期望的補償電流is。
本文采用的三相STATCOM系統結構如圖2所示。控制系統為雙閉環控制結構,檢測負載電流iload得到指令補償電流,經電流環控制器調節變流器輸出電流iSTATCOM,進而補償負載產生的諧波。其中θ為鎖相環得到的網側電壓相位。
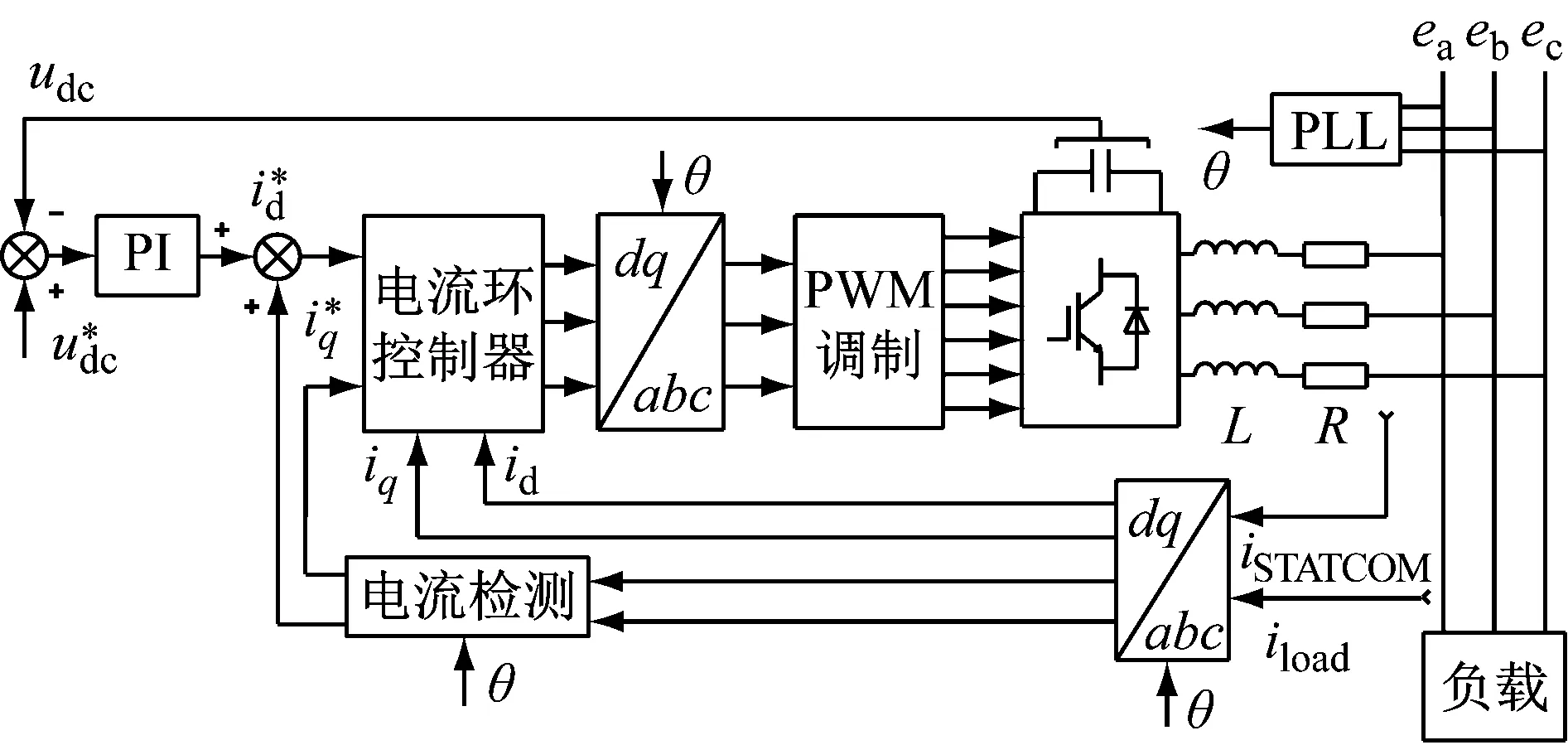
圖2 STATCOM系統結構圖
2 自適應分數階重復控制器設計
內模原理指出在閉環系統穩定的前提下,被控對象無靜差跟蹤輸入信號的充分必要條件是控制器內包含輸入信號產生的模型[11]。重復控制是一種基于內模原理的控制策略,其傳遞函數可以展開為
(3)
可以看到,重復控制可以等效為若干諧振環節相并聯的形式,理論上在各諧振點nω處都具有無窮大的增益,可以實現對該頻率下正弦信號的無靜差跟蹤。
圖3(a)為STATCOM電流環結構框圖,圖中:Gc(z)為電流環控制器;G2(z)為重復控制器。為了提高系統響應速度常數和比例環節G1(z)復合使用;R(z)為電流參考信號;E(z)為偏差信號;Y(z)為電流環輸出信號;D(z)為擾動信號;P(z)為被控對象,GPWM(z)為變流器傳遞函數。重復控制器G2(z)具體結構如圖3(b)所示,虛線框部分是內模環節。
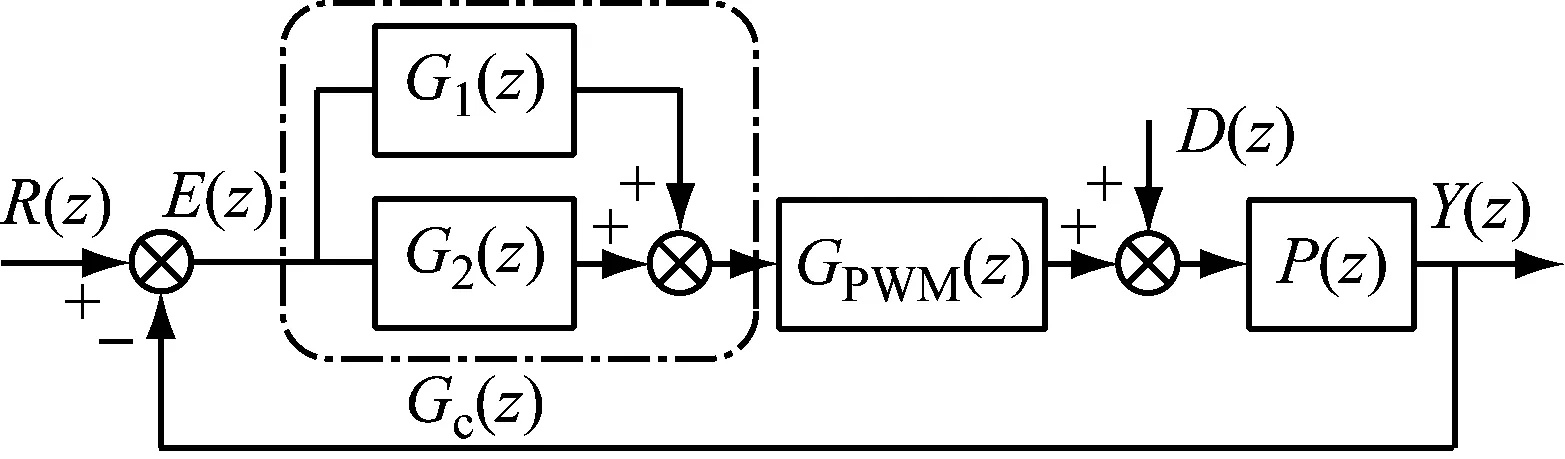
(a) 控制系統框圖
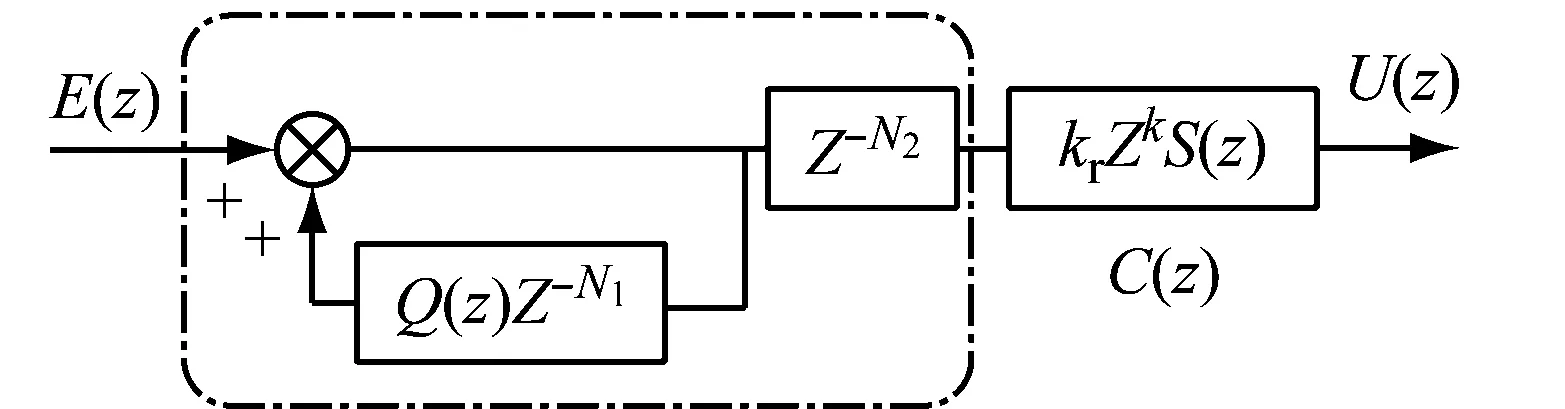
(b) 重復控制器框圖
圖3 STATCOM電流環結構框圖
2.1 自適應分數階重復控制內模環節設計
在如圖3(b)所示的傳統重復控制器中,離散域相位滯后環節階次N1、N2只能取整數,且N1=N2=fs/fm,為采樣頻率fs和網側基波頻率fm的比值。當電網工作在額定頻率時,fs、fm呈整數倍關系,重復控制諧振頻率和電網頻率相同;當網側頻率波動時,fs、fm可能呈非整數倍關系,導致N1、N2與期望的分數階相位滯后階次產生誤差。N1的誤差會使控制器諧振頻率偏離電網頻率,導致系統補償精度下降;N2的誤差會導致相位超前補償Zk階次產生誤差,所以N1、N2的偏差均會降低控制器的補償性能。
采用一種基于拉格朗日插值多項式近似分數階相位滯后環節的方法,將圖3(b)傳統重復控制中內模部分整數階滯后環節N1、N2替換為分數階滯后環節Z-Nq,改進后的內模結構如圖4所示。
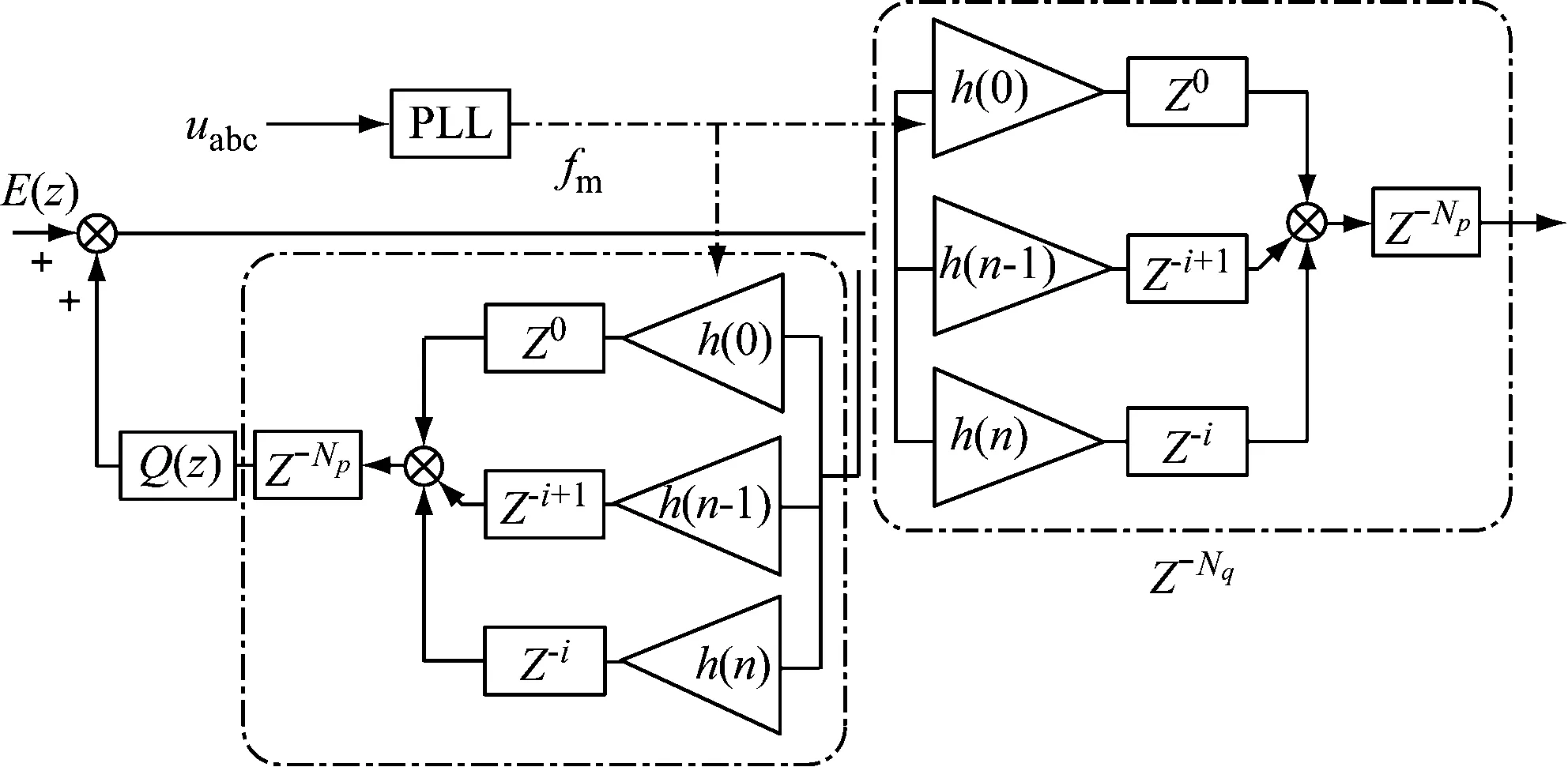
圖4 改進的內模結構
對改進后內模環節的分數階相位滯后Z-Nq采用n階多項式逼近的方法,Z-Nq可近似表示為
(4)
式中:Nq是期望的分數階相位滯后階次;Np取最接近Nq-n/2的整數。
根據Oetken的理論[12-13],
(5)
理論上當多項式階數n趨于無窮時可以無限逼近期望的分數階滯后環節,實際中考慮計算量和精度,取n=3,D取Nq-Np,表示Nq的小數部分。
綜合式(4)、(5),推導可得任意階次分數階相位滯后環節的3階近似多項式通式:
(6)
采用自適應分數階重復控制策略,在電網頻率波動時,根據鎖相環(PLL)計算的實時網側電壓基波頻率fm與數字系統采樣頻率fs得到期望的相位滯后階次Nq,結合式(6)得到分數階滯后環節的近似多項式系數h(n)。通過數字系統在線調整圖4所示內模環節的參數,保證相位滯后階次等于fs/fm,從而使重復控制器諧振頻率實時跟隨電網頻率的變化。
2.2 補償器設計
kr為重復控制增益,一般取小于1的數,其大小和誤差的收斂速度呈正相關,與控制系統的穩定裕度呈負相關。
補償濾波器S(z)使系統在低頻段保持零增益,并提高系統的高頻衰減性能。從分析可知,電流環被控對象P(s)等效為一個慣性環節1/(Ls+R)。根據經典控制理論的期望函數校正法,設計補償濾波器的復頻域表達式:
(7)
超前環節Zk用來補償被控對象P(z)和S(z)帶來的相位滯后,使系統在低頻段接近零相移。
2.3 穩定性分析
由圖3、4可知,本文所提的電流環控制器傳遞函數Gc(z)可以表示為:
(8)
誤差傳遞函數E(z)可以表示為
(9)
E(z)的特征多項式
H1(z)=1+Gc(z)GPWM(z)P(z)
(10)
當系統頻率足夠高時,控制系統近似無延時,即GPWM(z)=1。將式(8)代入(10),可得:
H1(z)=
(11)
設
(12)
將式(8)、(12)代入式(11)中,可得:
(13)
令
根據式(13)~(15)可知,電流環控制器穩定需滿足以下兩個條件:①H3(z)的根分布在單位圓內;② 在滿足條件(1)時,根據小增益定理[14-15],控制器穩定的充分條件為在奈奎斯特頻率范圍內H2(z)的模值小于1。考慮到參考信號為周期性信號,且典型環節|Z-n|=1,對H2(z)化簡可得式(16)所示的H4(z),即控制器穩定的充分條件為|H4(z)|<1。
H4(z)=Q(z)-krZkS(z)G3(z)
(16)
3 控制器參數設計與仿真分析
本文研究的三相STATCOM系統具體參數:相電壓有效值us=25 V,交流電壓額定頻率f0=50 Hz,采樣頻率fs=10 kHz,交流側電感L=3 mH,交流側線路阻抗R=0.36 Ω,直流側電容C=1 mF,直流側電壓給定udc=65 V。
3.1 控制系統參數設計
依據上文所述方法結合系統參數設計控制器。重復控制內模中Q(z)是低通濾波器,為了簡化計算,一般取Q(z)=0.92;重復控制增益kr取0.1。以基波20次諧波為界,將S(z)的截止頻率ω取2 000π,ξ取0.707,根據式(7)可得S(s),離散化后得:
(17)
S(z)對P(z)的補償效果如圖5所示。
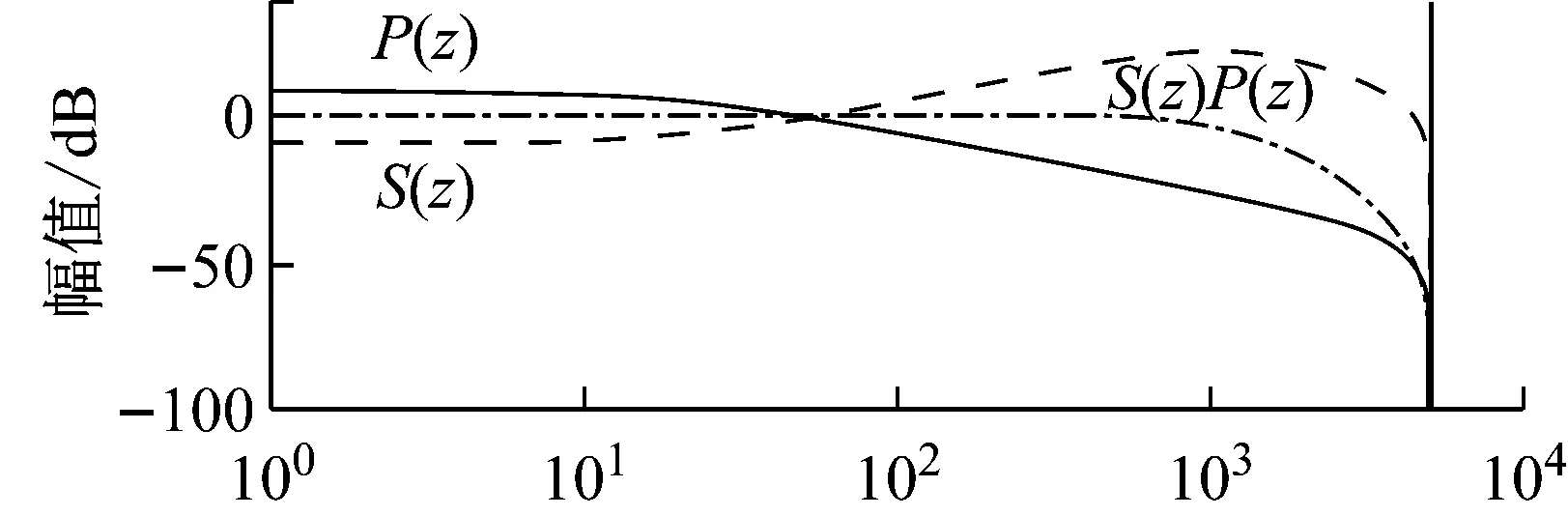
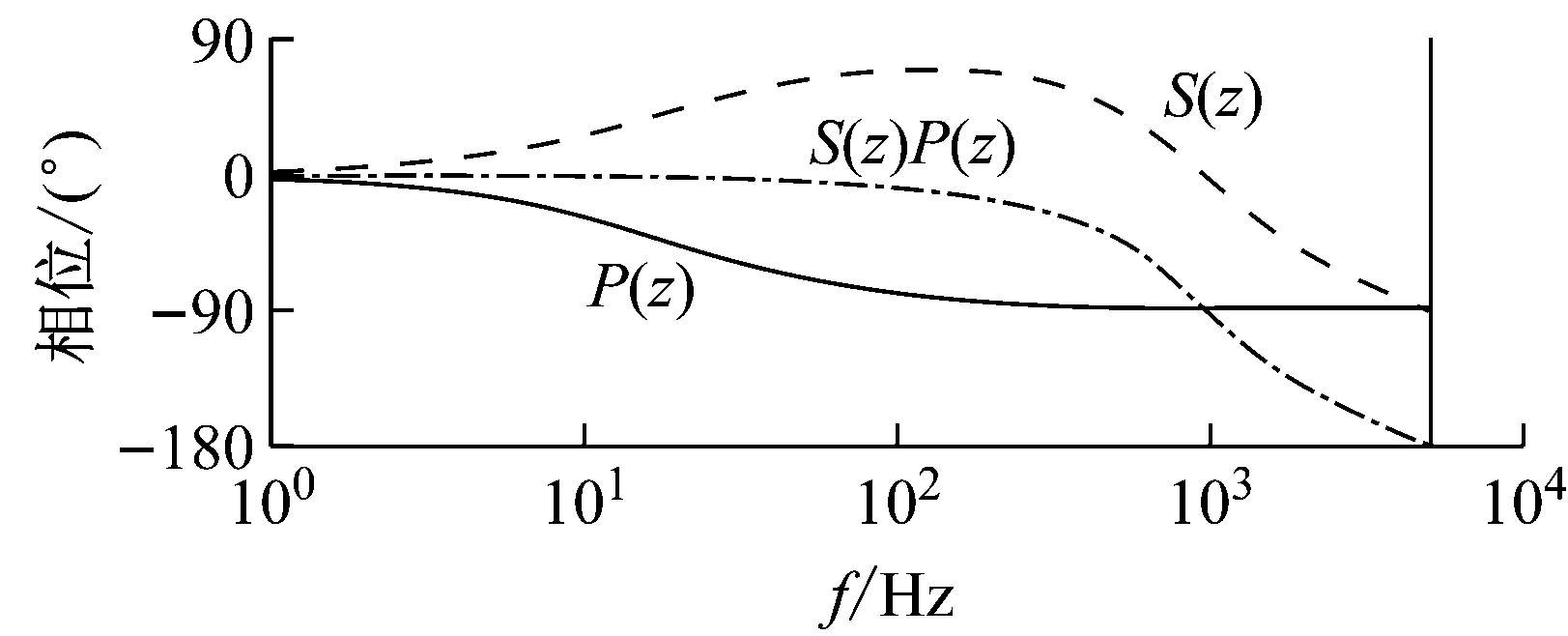
圖5S(z)補償效果圖
根據圖5設計超前環節Zk,補償由被控對象P(z)和濾波器S(z)帶來的相位滯后。超前環節對S(z)P(z)的補償如圖6所示。可以看到,當k=2時,超前環節近似地補償了系統的相位滯后。仿真中,考慮到數字系統一拍的滯后,實際取k=3。
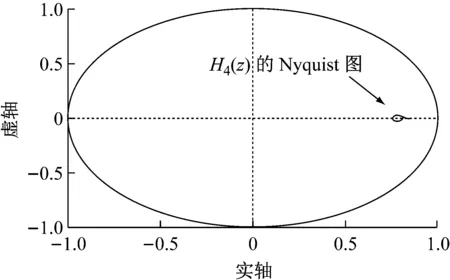
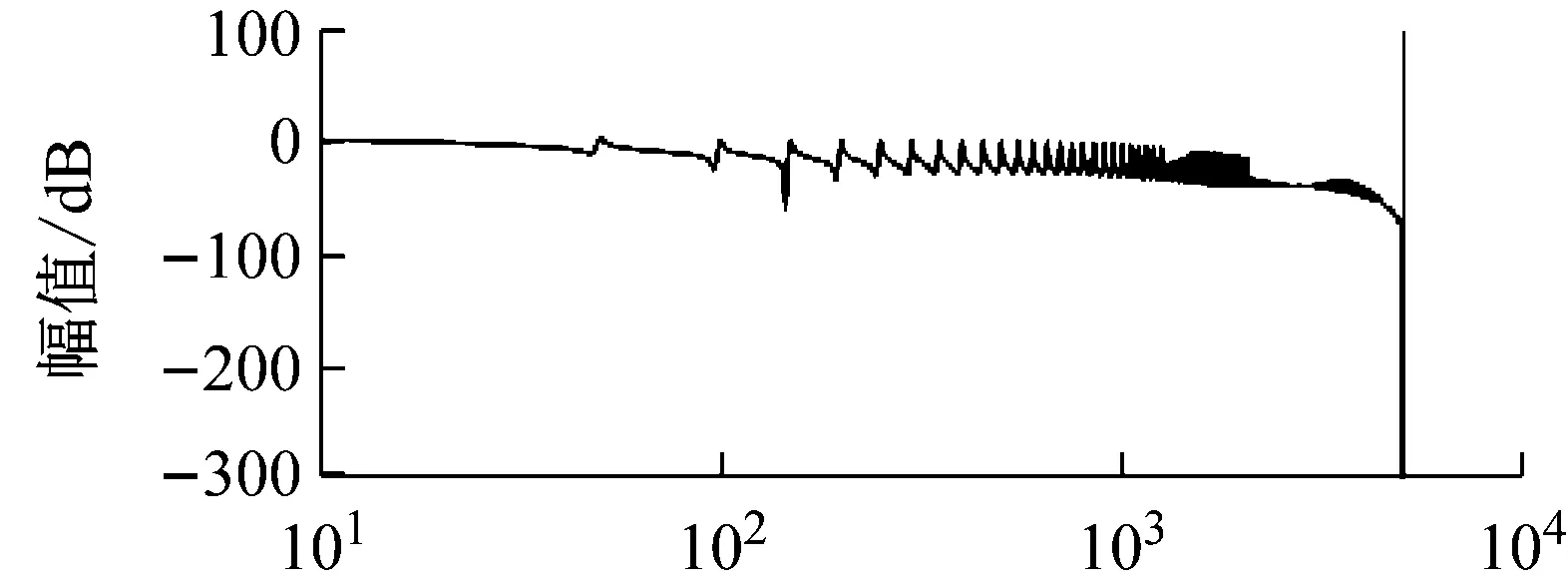
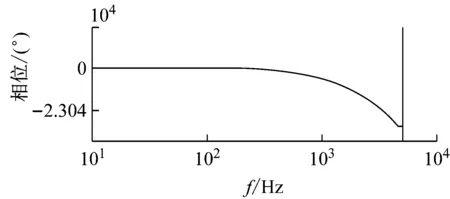
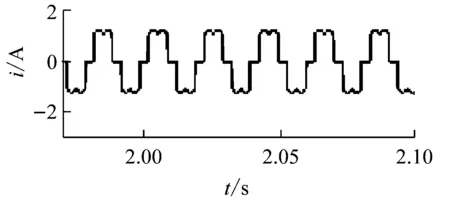
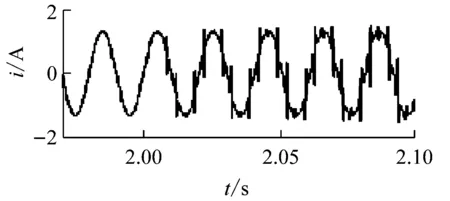
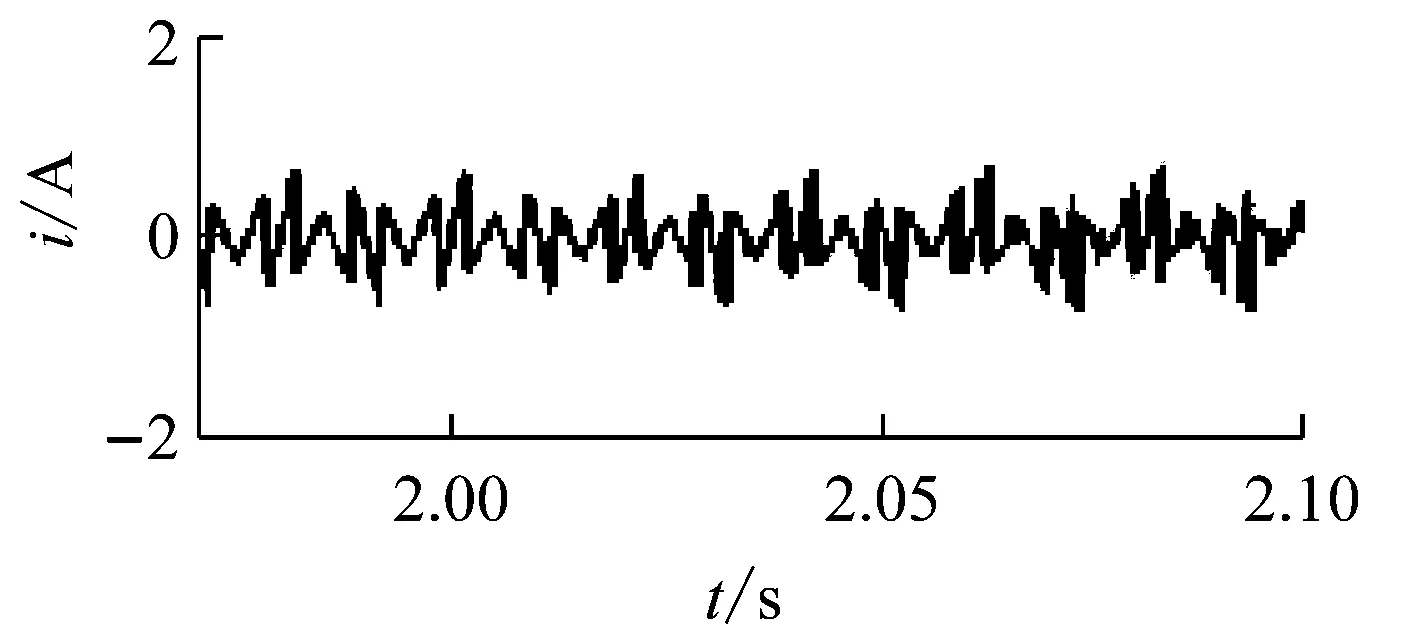
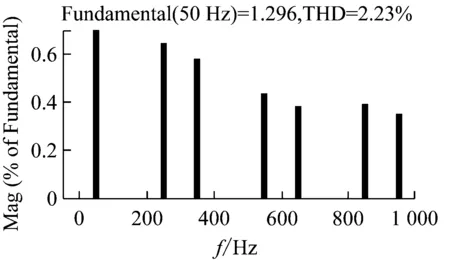
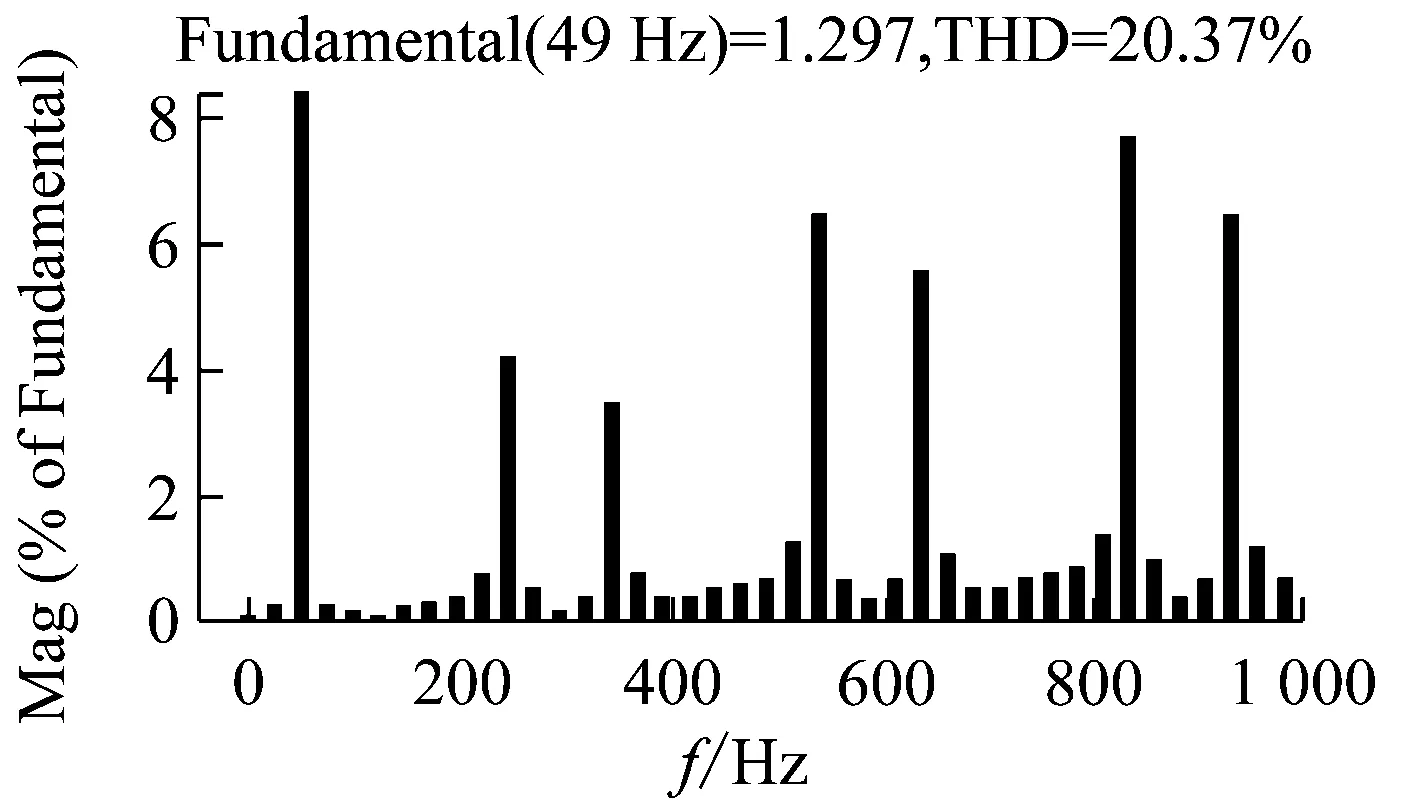
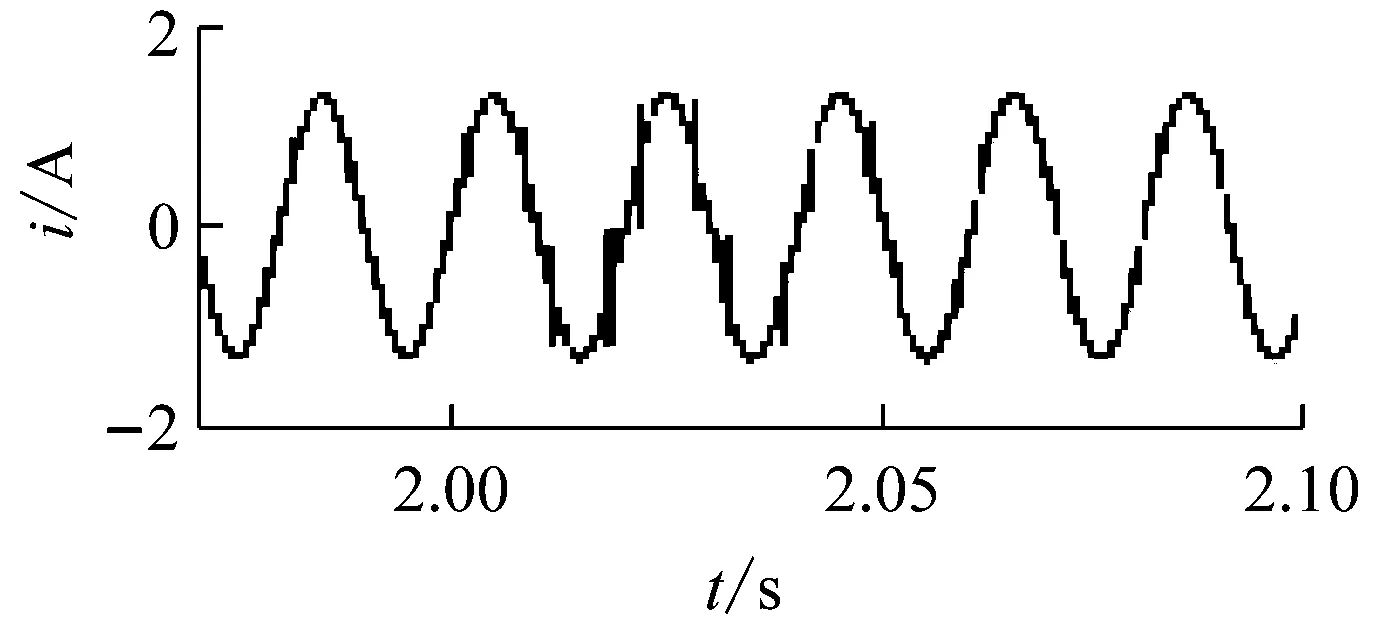
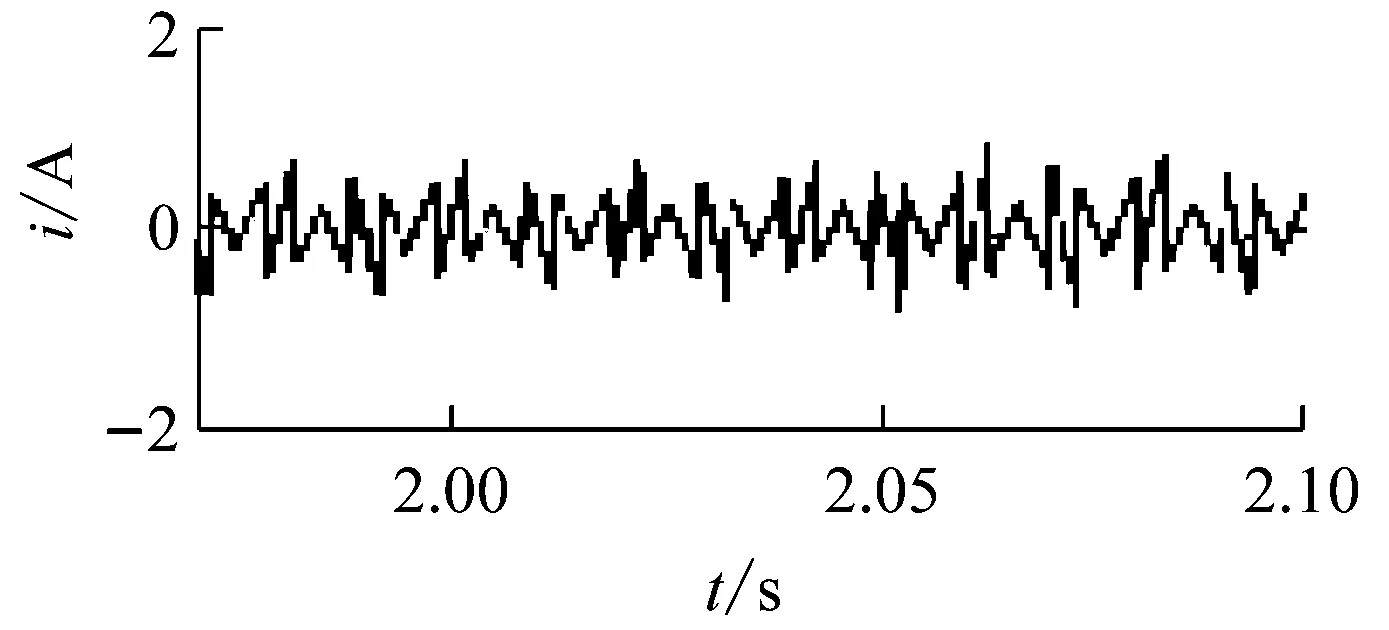
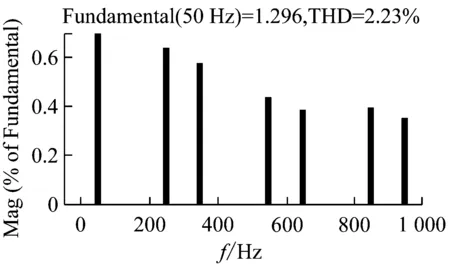
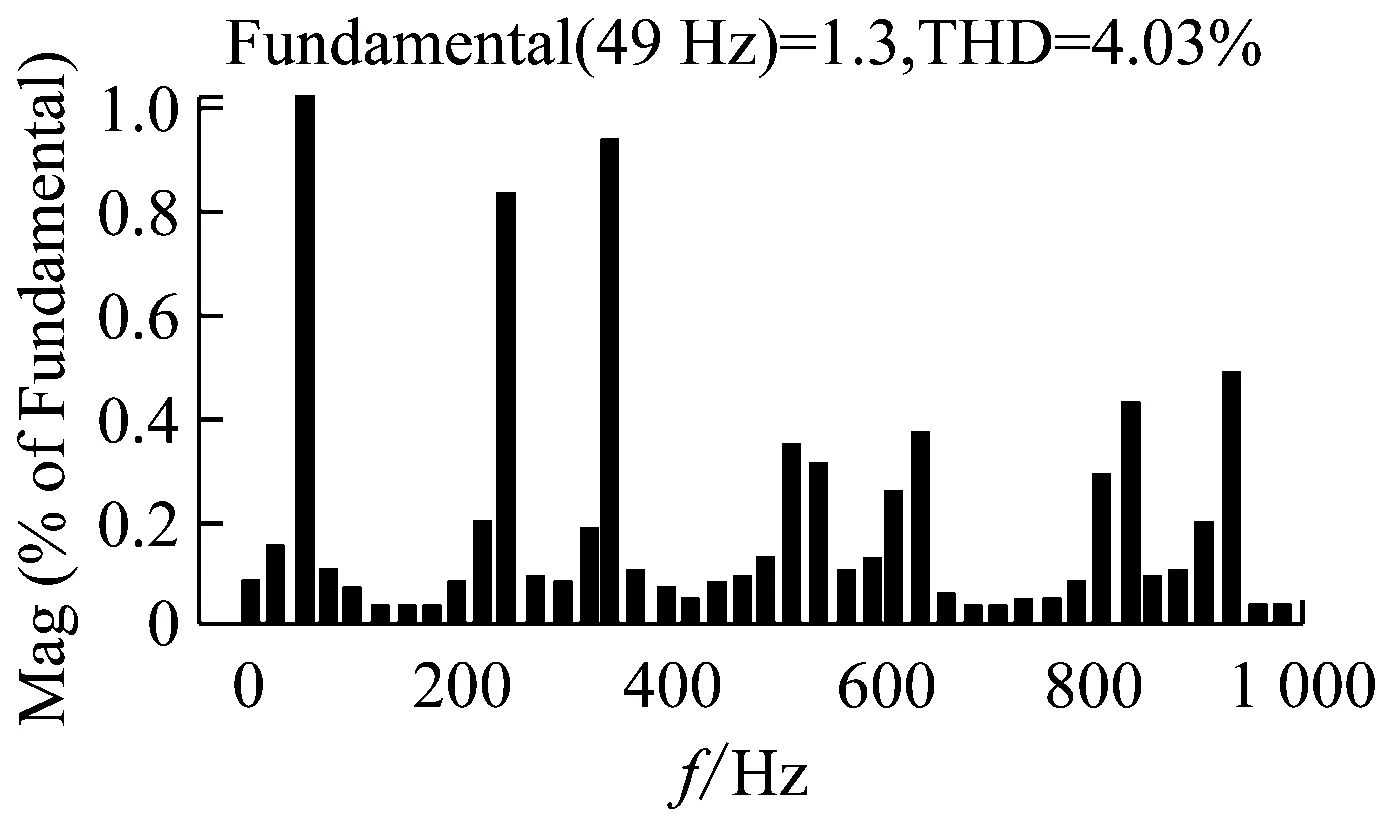
在控制系統穩定的前提下,kp的取值根據上文所述的穩定性判據①。繪制H3(z)隨kp變化的參數根軌跡如圖7所示,可以看到,當0 圖6Zk超前補償效果圖 圖7H3(z)隨kp變化的根軌跡 根據穩定性判據②,繪制H4(z)的離散域奈奎斯特曲線如圖8所示。可以看到H4(z)模值位于單位圓內,滿足穩定性判據②。 圖8H4(z)的Nyquist圖 繪制電流環開環波特圖如圖9所示。可以看到,系統在基波頻率及其整數倍頻率處均有較大的增益,且低頻段接近零增益、零相移。 圖9 電流環波特圖 根據上文的參數設計,在Simulink環境中搭建仿真模型,負載采用三相不可控整流器接50 Ω電阻作為非線性負載。為了驗證系統在電網頻率波動時的適應性,仿真設置在2.0 s時電網頻率從50 Hz躍變到49 Hz,對比傳統重復控制器和所提自適應分數階重復控制器在頻率波動時的適應能力。 圖10所示為傳統重復控制下系統的仿真波形。可以看到,在電網額定頻率50 Hz時,傳統重復控制可以保證好的補償效果,網側電流THD為2.23%;在頻率變化后,由于諧振頻率偏移額定電網頻率,控制器補償精度下降,電流THD增大到20.37%,超過了國標要求的范圍。 圖11是在相同條件下采用自適應分數階重復控制的仿真波形。當電網工作在額定頻率時,補償效果和傳統重復控制相同,電流THD為2.23%;在頻率變化時,系統經過調節后仍保證好的補償效果,網側電流THD為4.03%,在國標允許范圍內,故所提控制策略較傳統重復控制策略適應性更好。 (a) 負載電流 (b) 頻率波動時電網電流 (c) 頻率波動時補償電流 (d) 頻率波動前交流電流THD (e) 頻率波動后交流電流THD 圖10 傳統重復控制仿真波形 (a) 頻率波動時電網電流 (b) 頻率波動時補償電流 (c) 頻率波動前交流電流THD (d) 頻率波動后交流電流THD 為拓展STATCOM的補償帶寬,使系統在電網頻率波動時仍具備好的補償性能,本文采用一種自適應分數階重復控制策略。使用基于拉格朗日插值多項式近似分數階相位滯后的方法,根據電網實時頻率,在線整定控制器參數,實現了系統對電網頻率變化的適應性。在分析了系統原理和控制器設計方法的基礎上,進行仿真。結果表明,由于自適應分數階重復控制策略的引入,使得控制器諧振頻率可以跟隨電網頻率變化,提高了STATCOM的抗電網頻率波動能力,證明了控制策略的可行性。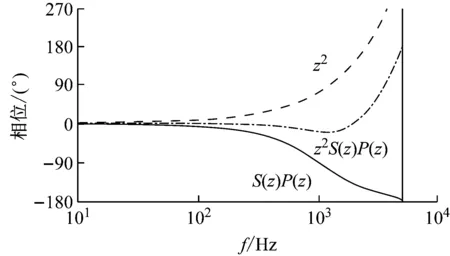

3.2 仿真分析
4 結 語

