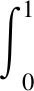一種圖像清晰與模糊的判別方法

傅志中， 王琦藝， 李曉峰， 徐 進

(1.電子科技大學 信息與通信工程學院,成都 611731；2.昆明物理研究所,昆明 650223)

0 引 言

在實際應用場景中，由于人為操作原因或拍攝場景惡劣，傳感器失真等原因都會導致圖像質量降質，其中一種最常見的圖像降質為圖像模糊[1]。當前大量圖像處理應用及實驗教學應用中，如圖像分割[2]、目標提取與識別[3-5]等，都假設待處理圖像是清晰的。文獻[6-7]中研究了運動原因導致圖像模糊的運動去模糊技術，實現了模糊圖像的清晰化處理，為后續圖像處理任務提供清晰化圖像。但是，由于模糊函數的病態特性，損失的信息不可恢復，基于算法復原的圖像清晰度仍然不能滿足應用需求。因此，迫切需要對圖像的模糊與清晰程度進行預先判定，剔除模糊圖像，僅保留清晰圖像用于圖像處理任務，提高圖像處理任務性能。

圖像模糊檢測方法可大致分為三類：提取圖像特征進行閾值設定,建立評價模型對圖像進行評估,利用圖像摳圖方法定位模糊區域。基于上述3類方法的模糊判斷有：段興濤等利用圖像的四向差分特征，用閾值法判斷模糊圖像的存在；文獻[8-10]中利用圖像的邊緣梯度分布的擬合標準差、Haar小波分解的邊緣類型判斷出圖像邊緣的模糊程度；Su等[11]提出利用圖像像素奇異值之間的關系，直接實現圖像的模糊區域定位。

近幾年又發展出了基于DA的模糊圖像識別方法[12]，該方法基于LMDR度量學習，提高了模糊圖片的識別性能，但其需要前期大量的樣本進行學習訓練，過程繁瑣且不能給出圖像模糊程度的定量描述。文獻[13]中提出了利用頻率系數統計特征、峰度值、顏色飽和度三方面作為圖像特征來進行圖像模糊判定，該方法針對灰度圖像將失效并且特征建立過程繁雜。上述模糊識別算法均涉及較多的圖像特征提取與建模過程，在很多惡劣場景下，這些特征并不能被有效和準確地提取。

本文提出了一種基于圖像頻譜分段信息的圖像清晰與模糊判別與衡量方法。根據圖像頻譜分布的統計特性可對模糊與清晰圖像進行分類，同時給出模糊程度的定量描述。

1 圖像的頻譜分析

對灰度圖像I(x,y)∈{0,1,…,255},若尺寸為M×N，其二維傅里葉變換定義為[14]

(1)

為了更直觀地顯示圖像在頻域的能量分布情況，通常要將圖像的傅里葉變換結果進行搬移，將原點移至中心，這一過程可通過對原始圖像乘以(-1)x+y實現。同時,因為傅里葉變換結果為復數,因此還需對結果取絕對值,得到的二維圖像的頻譜如下：

S(u,v)=abs(F(-1)x+yI(x,y)(u,v))

(2)

需要指出的是,因為圖像為二維實信號，因此，其中心化的傅里葉頻譜是關于原點中心對稱的[15]，如圖1所示。

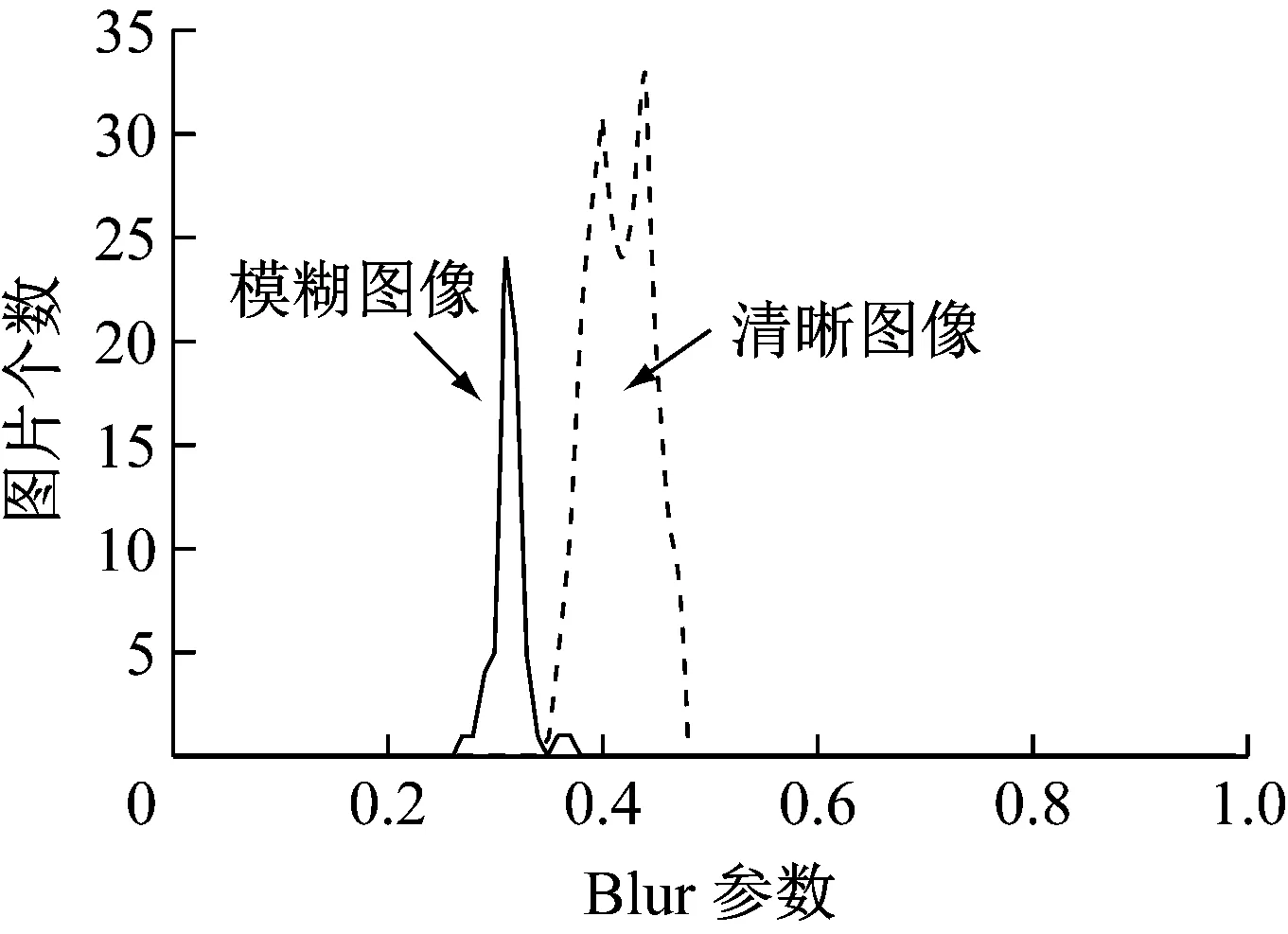
信號頻譜的低頻部分對應時域中變化變化緩慢的部分，即圖像的平滑區域;反之，高頻部分對應圖像的邊緣，紋理等高頻信息。模糊圖像的邊緣與紋理等高頻信息受模糊影響被削弱，而平滑區域等低頻信息基本不受影響。清晰圖像因為有豐富的邊緣、紋理等高頻信息，因此其頻譜能量在高頻區域分布多于模糊圖像。

原圖

中心化傅里葉頻譜

圖1 原始圖像與傅里葉頻譜

2 基于頻譜分布的模糊判定方法

基于模糊圖像與清晰圖像在頻譜分布上的差異特性，本文提出了一種判別模糊圖像與清晰圖像的方法，其流程如圖2所示。

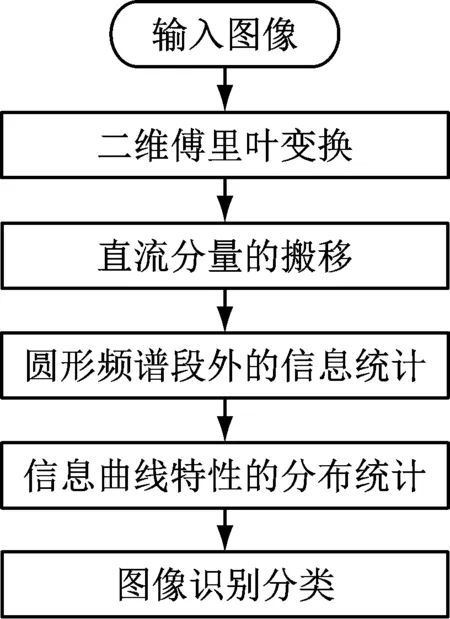
圖2 算法整體流程圖

首先對灰度圖像進行傅里葉變換得到其中心化的頻譜信息，隨后取以原點為圓心，半徑從1逐漸增大的圓形區域，計算這些圓形區域外的平均歸一化頻譜能量，得到頻譜能量分布曲線。通過統計曲線下部的積分面積即可求得歸一化的模糊程度衡量參數。基于不同具體場景，設定不同閾值即可在該場景下有效的區分模糊與清晰圖像。

2.1 圓形段外頻譜信息統計

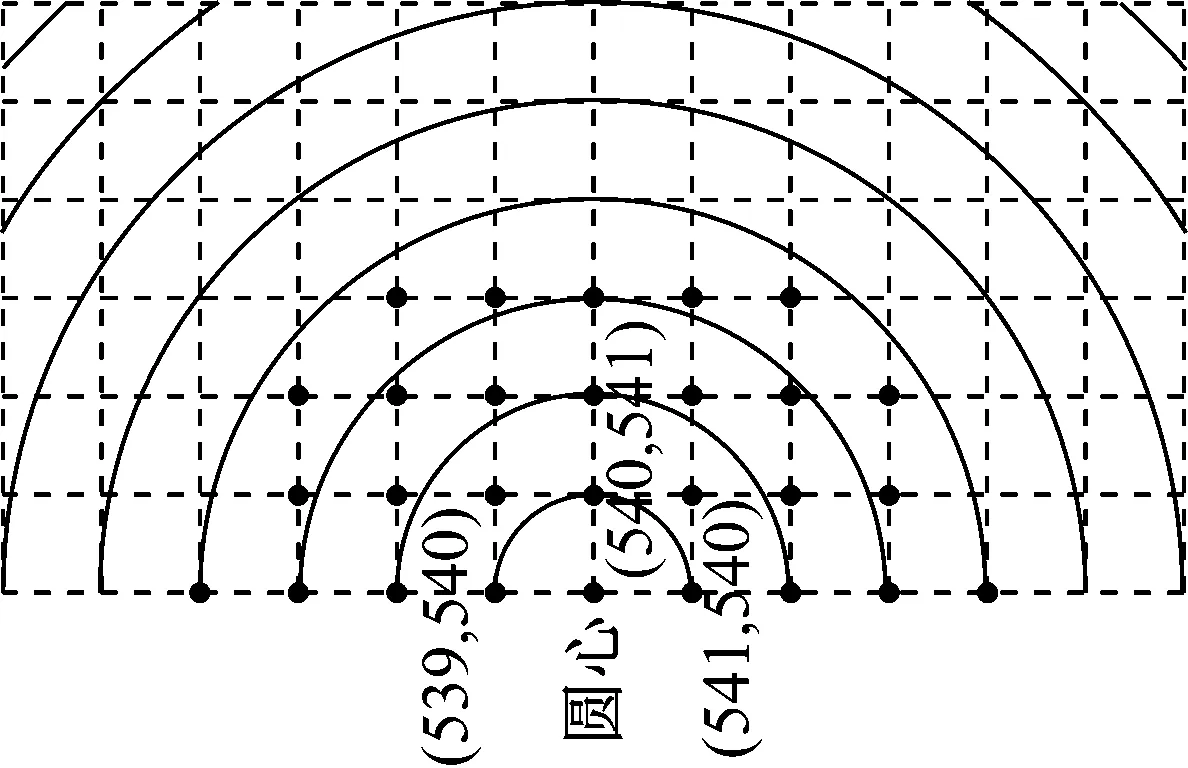
針對中心化之后的圖像頻譜，對頻譜分布進行了統計。以一幅大小為a×a的圖像為例，其中心化之后的頻譜為一個a×a的實矩陣，由實信號頻譜的對稱特性可知，只需統計中心點一側的頻譜分布即可。為統計該頻譜分布，首先定義以頻譜中心原點為圓點以r為半徑的圓形區域：

C(r)=

(3)

式中,(u0,v0)為中心化之后的頻譜中心點坐標，且由圖像尺寸限制可知r

由式(3)，以a=1 080時依次增大r所確定的圓形區域如圖3所示。由圖像頻譜性質可知，圓形區域外的點頻率相對高于圓形區域內的點。為統計圓形區域外點的歸一化平均能量，定義如下統計參數：

(4)

圖3 圓形區域示意圖

即頻譜的總體能量減去圓內能量得到不同半徑下圓外的剩余能量，并除以圓外點的個數進行平均。

2.2 圓外剩余能量變化曲線

通過由小到大遍歷r的可能取值，并取：

(5)

用來表征圓外高頻能量相對于初始能量的相對變化程度。將r歸一化之后，可以得到類似圖4所示的頻譜能量變化曲線。該曲線刻畫了隨著圓形半徑的增大，圓外剩余能量相對頻譜初始總能量的變化規律。圖中虛線對應清晰圖像，實線對應同一場景的模糊圖像，可見在歸一化頻率較小時，即圓半徑較小時，隨著半徑增大，圓外剩余能量比例在模糊圖像中下降較快，而到了高頻部分，即圓半徑較大時，隨著半徑增大，模糊圖像中的剩余高頻能量比例下降變慢。這一規律反映了模糊圖像的能量分布大多在低頻區域，而清晰圖像的能量在高低頻分布相對均勻這一客觀事實。

圖4 頻譜剩余能量變化曲線

2.3 模糊程度判別參數

圖4所示的曲線形狀可以有效區分不同模糊程度下的圖像，為了將曲線形狀轉化為一種有效率的客觀指標來衡量圖像的不同模糊程度，需要尋找一種指標區分圖4中的兩條曲線。本文采用如下定義：

(6)

通過對Ratio(r)曲線進行積分，求得曲線下部的面積，該參數可以有效區分圖4中的兩條曲線，面積較大的曲線對應于模糊程度較低的圖像，同時由式(6)可知Blur∈(0,1)。

當采用本文方法對一組圖像進行模糊和清晰分類時，可以先由圖像集中選出若干組清晰與模糊圖像樣本，分別求得樣本的Blur參數，通過樣本集中該參數的分布情況，確定一個最佳判決門限T，從而對數據集中的任一圖像，其模糊判決結果如下：

(7)

式中:i為圖像集中任一圖像的編號;Flag為最終判決輸出結果;1為模糊圖像;0為清晰圖像。

3 實驗結果與分析

針對本文提出的模糊圖像判定方法，為了驗證該方法的有效性與靈敏度，對清晰圖像進行不同程度的高斯模糊并統計頻譜中不同頻率外的剩余能量比例下降情況，如表1所示。表中圓外剩余能量變化繪成曲線如圖5所示。

表1 不同模糊程度下的圓外能量變化

圖5 同一場景，不同模糊程度下的曲線分布圖

由圖5曲線分布可以看出，不同模糊程度下的曲線分布存在明顯差異，有較好的區分度。同時清晰圖像所對應曲線的積分面積明顯高于其他模糊圖片且該指標與清晰程度成正相關，即隨著高斯模糊方差從0.5增大到1.5，曲線下方面積逐漸下降。表明本文所提方法與指標可以很好地定量衡量圖像的清晰程度。

針對某一具體場景，為了確定式(7)中的最佳判決門限值T，實現最佳模糊與清晰分類邊界，在本實驗數據集下，選取模糊與清晰樣本各一組，分別求得其Blur參數，并畫出清晰圖像與模糊圖像的參數分布曲線，如圖6所示。圖中橫軸為Blur參數可能取值;縱軸為該樣本集中Blur參數取某一特定值的圖片個數;虛線為清晰圖像的參數分布;實線為模糊圖像的參數分布。根據樣本中的參數分布情況可知，當判決門限T取在紅色虛線所示位置時，針對該場景，可以取得最佳的區分結果，從而確定了最佳門限值。

圖6 樣本集中參數分布曲線

4 結 語

本文提出了一種基于頻譜段信息的圖像清晰與模糊判別特征提取方法，設計了一種圖像頻譜分析方法，借助清晰與模糊圖像在頻譜能量分布上的差異，有效的解決了清晰與模糊圖像的分類問題。同時，本文提出的Blur參數可用于定量地對圖像的模糊程度進行度量，本文算法擁有過程快速、簡便，分類區分度高等優點。