電網故障的正余弦診斷方法

熊國江， 張 靖， 何 宇

(貴州大學 電氣工程學院，貴陽 550025)

0 引 言

快速準確地診斷出電網故障的元件是實現智能電網自愈的基礎[1]。國內外學者就該問題開展了大量的研究工作，提出了多種診斷方法，包括專家系統、粗糙集、神經網絡、Petri網、優化技術等。其中，專家系統故障診斷方法可以充分利用專家的經驗知識，但知識的維護和更新較為困難，故障容錯性差；粗糙集故障診斷方法通過屬性約簡可以有效提高故障容錯性，但對電網結構變化的適應性較差；Petri網故障診斷方法透明度高，但故障容錯性有待進一步加強。與上述方法不同，優化技術故障診斷方法的數學模型理論性強，模型構建簡單，是一種應用前景良好的故障診斷方法，近年來得到了快速發展。該方法先根據電網元件、保護和斷路器之間的邏輯關系構造一個反映實際報警信息與期望報警信息之差的數學模型，將故障診斷問題轉化為一個0-1整數規劃問題，然后采用粒子群優化算法[2]、蜜蜂群算法[3]、差分進化算法[4]、生物地理學優化算法[5]等優化技術求解該規劃問題，從而找到最能解釋各個保護和斷路器的動作行為的故障假說。近年來,優化技術的快速發展,有力助推了該方法的應用研究。

由“沒有免費的午餐”理論[6]可知，沒有任何一種優化方法能在電網故障診斷問題上永遠保持最優，因而有必要挖掘更多可求解電網故障診斷問題的優化方法，探討其在該問題上的可行性和有效性，豐富電網故障診斷的求解思路。正余弦優化算法(Sine Cosine Algorithm, SCA)[7]是近年來提出的一種新的智能優化算法，采用正弦函數與余弦函數完成迭代運算，其設計遵循簡單、快速的原則，算法無需額外調節的參數，從而提高了應用的便利性，已在很多問題[8-14]上得到了廣泛應用。

本文將SCA算法應用到電網故障診斷中，根據電網故障診斷問題的特點設計了二進制SCA算法，并采用不同類型算例從不同角度驗證了該方法的優化性能。實驗結果表明，與遺傳算法GA和粒子群算法PSO相比，SCA算法可以快速獲得更加準確的診斷結果。

1 電網故障診斷數學模型

電網故障診斷問題在數學上可描述為如下典型的0-1整數優化問題：

(1)

式中:D表示故障區域內可能故障元件數；Si為第i個元件的故障狀態，1表示故障，0表示完好。

電網故障后，繼電保護系統中的相應保護將會動作，斷開相關的斷路器，從而隔離故障元件。通過分析這些保護和斷路器的動作行為可以診斷出故障元件。基于優化技術的電網故障診斷就是尋找最能解釋各個保護和斷路器的動作行為的故障假說。其目標函數[5,15]為：

minF(S)=

(2)

式中：r和C分別表示保護和斷路器；*表示期望狀態；m、p、s、mal和dir分別表示主保護、近后備保護、遠后備保護、失靈保護和方向元件；∑⊕的計算規則為：累加數≠0，取1，否則,取0;wm、wp、ws、wmal、wdir和wc為權值，取值分別為0.9、0.8、0.7、0.7、0.85和0.95[5]。

2 二進制SCA算法

2.1 基本SCA算法

SCA的設計遵循簡單、快速的原則，每個個體可表示為，i=1,2,…,NP，NP為種群規模。SCA的迭代過程僅僅依據下式所示的正弦函數與余弦函數實現：

(3)

(4)

式中:P=[p1,p2,…,pD]為最優個體；r1隨機分布于(0,1)范圍內;r2隨機分布于(0,2π)范圍內;r3隨機分布于(0,2)范圍內。

SCA在迭代過程中，采用一個(0,1)范圍內的隨機數r4來選擇式(3)或(4)，流程如下：

初始化種群X=[X1,X2,…,XNP]

計算種群所有個體的目標函數值

初始化迭代次數t=1

While終止判據未滿足do

通過目標函數值確定最優個體P

fori=1 toNPdo

ford=1 toDdo

生成隨機數r4

ifr4<0.5 do

采用式(3)更新xi,d

else

采用式(4)更新xi,d

end if

end for

end for

計算所有更新個體的目標函數值

t=t+1

End while

2.2 二進制SCA算法

本文采用sigmoid函數實現實數編碼到二進制編碼的轉換，其方式如下：

(5)

轉換規則為：

(6)

式中，rand(0,1)表示(0,1)之間的隨機數。

3 基于二進制SCA的電網故障診斷流程

采用二進制SCA求解電網故障診斷問題的流程如圖1所示。首先確定停電范圍，停電范圍內的設備均列為可能故障元件，然后按照式(2)構造這些可能故障元件對應的目標函數，最后采用二進制SCA進行優化求解，從而診斷出故障元件。

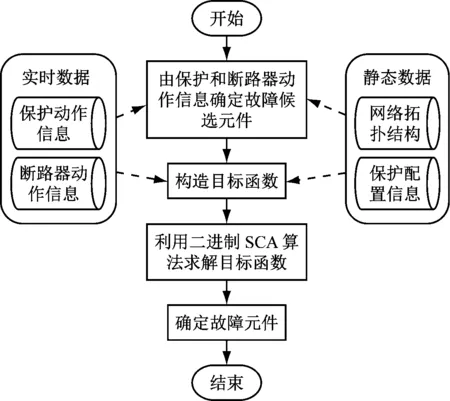
圖1 基于二進制SCA的故障診斷流程

4 算例分析

4.1 測試系統

本文采用如圖2所示的電力系統作為測試系統。

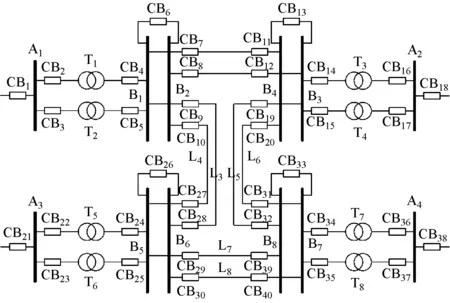
圖2 測試系統

為了測試SCA的優化性能，采用GA和PSO進行對比，分別計算100次。仿真實驗條件：3.70 GHz CPU，8 GB內存，Matlab R2010b。對于所有算法，NP=10，最大迭代次數Tmax=50。采用文獻[5，15]中的6個故障算例來檢驗SCA算法的故障診斷能力，如表1所示。

4.2 故障診斷準確性結果分析與比較

表2為3種算法在6個測試算例上的診斷結果。由表可知，SCA均能100%正確診斷出故障元件，而GA和PSO均存在錯誤診斷的情形。由比較結果可知，SCA在診斷準確性方面優于GA和PSO。

表1 測試算例

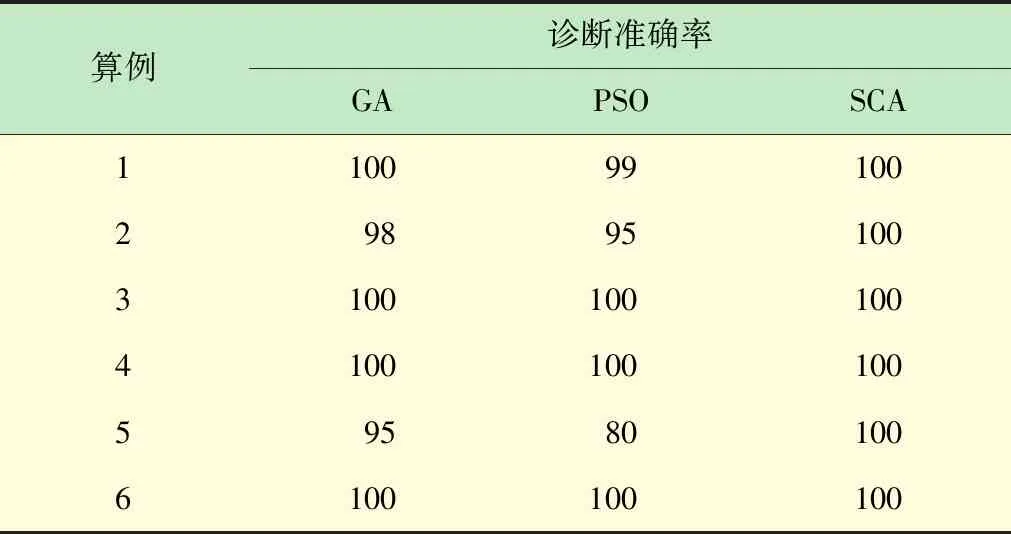
表2 故障診斷準確率比較

部分算例(算例1、3、5)的收斂曲線如圖3～5所示。由圖可知，SCA具有良好的全局快速收斂特性，而GA和PSO存在不能有效收斂的情形(如算例1和算例5)，這也從另一角度說明這兩種算法存在錯誤診斷的情形；雖然GA和PSO在算例3上能有效收斂，但收斂速度均滯后于SCA。此外，從圖中還可知，故障復雜度越大(如算例5)，SCA的優勢越明顯，說明SCA算法在處理復雜故障情形方面具有較強的能力。

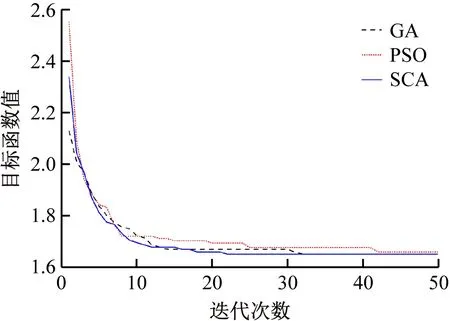
圖3 算例1收斂曲線

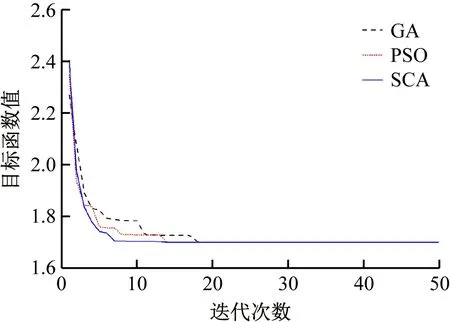
圖4 算例3收斂曲線

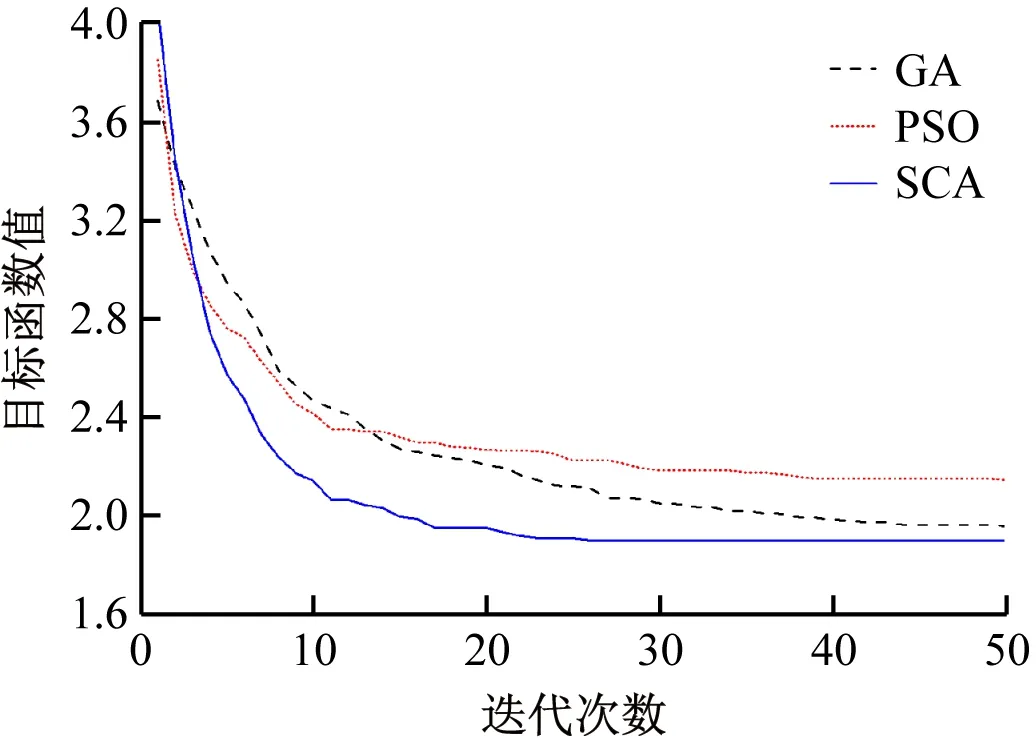
圖5 算例5收斂曲線

4.3 故障診斷快速性結果分析與比較

由表3可知，SCA的診斷速度最快，比PSO快8.3%～32.0%不等，而比GA快22.7%～93.9%不等。可知SCA在診斷快速性方面也明顯優于GA和PSO，這也正是SCA遵循簡單、快速的設計原則的結果。

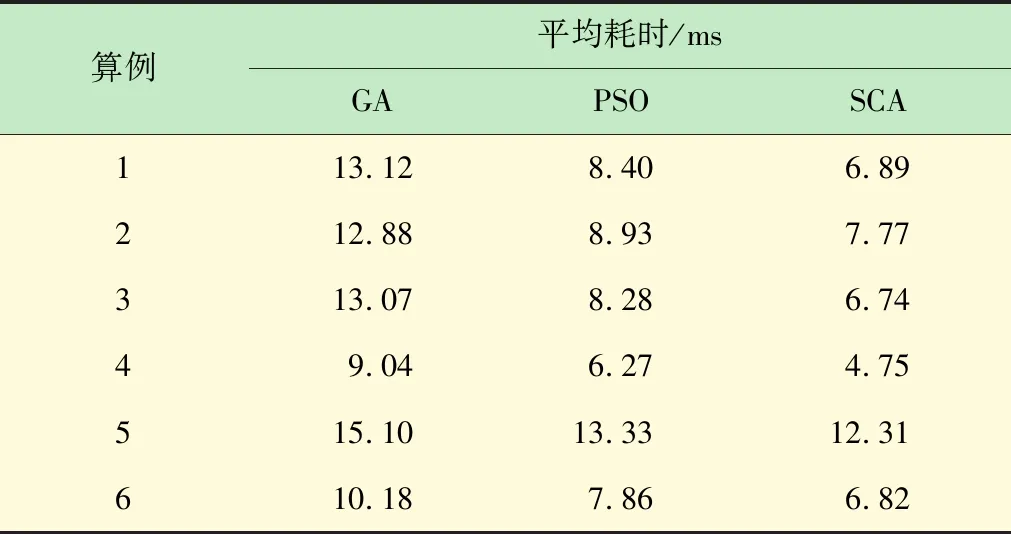
表3 故障診斷快速性比較

4.4 算法參數影響分析

SCA的一個主要特點是除了需要設置種群大小和迭代次數這兩個所有智能優化方法都需要設置的參數外，沒有額外需要設置的參數。雖然如此，由SCA的基本流程可知，該算法主要受隨機參數r1和r3的影響，其中r1為縮放因子，主要控制算法步長;而r3為指引因子，主要控制最優個體的參與度。

(1) 隨機數r1的影響分析。根據r1的特點設計了5種隨機取值方式：① (0,0.1)；② (0,0.5)；③ (0,1)；④ (0,5)；⑤ (0,10)。采用最復雜的算例5對各種分布方式進行分析，結果如圖6所示。由圖可知，SCA的確受隨機數r1取值的影響，r1取值太大或太小均不利于算法的診斷性能。究其原因，是因為r1作為縮放因子，用于協調SCA的全局探索(exploration)能力和局部開發(exploitation)能力。r1越大，exploration能力得到提升，同時也降低了SCA的收斂速度；r1越小，exploitation能力增強的后果是使SCA易陷入局部尋優，發生早熟。上述仿真結果表明，雖然r1采用隨機方式生成，但隨機范圍的選取需要綜合協調exploitation與exploration，兩者盡量達到平衡。

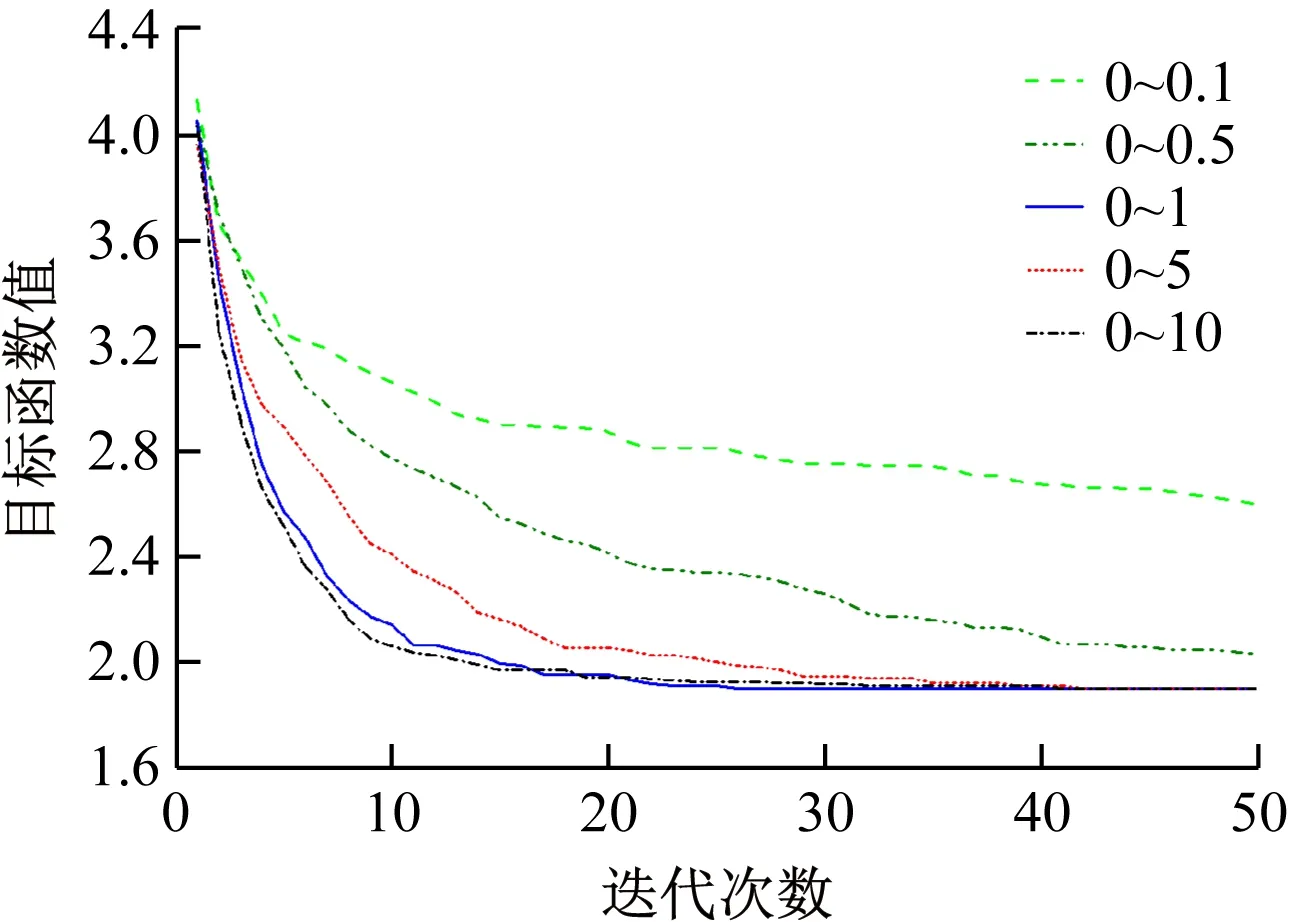
圖6 參數r1影響結果

(2) 參數r3的影響分析。針對r3設置了3種隨機取值方式：① (0,2)；②(0,1)；③(1,2)。同樣采用算例5進行分析，其結果如圖7所示。由圖可知，r3也同樣影響SCA的診斷性能。當r3為(0,1)時，最優個體P的參與度較弱，SCA搜索的方向性不強，收斂速度較慢；r3為(1,2)時，P的參與度較強，SCA容易陷入局部極值；r3為(0,2)時，可以有效平衡P的參與度，從而實現explitation與exploration的有效協調。

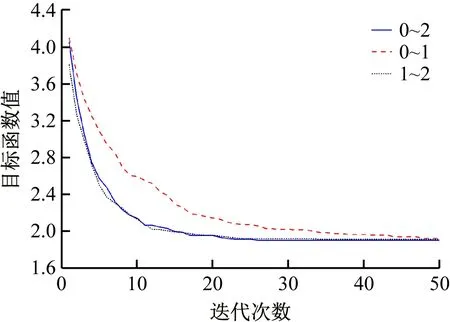
圖7 參數r3影響結果

5 結 語

本文將SCA算法應用到電網故障診斷問題中。采用不同類型故障算例從準確性、快速性、收斂性等角度來驗證該診斷方法的有效性。仿真結果表明，SCA算法可以快速有效處理多種復雜故障情形。SCA算法的縮放因子和指引因子均會影響SCA的診斷性能，合理的隨機數生成范圍的選取可以有效平衡全局搜索和局部搜索。下一步將采用正交學習策略、參數自適應等方法進一步提高SCA的優化性能，并用于求解經濟調度問題。