球形全向移動自平衡機器人的建模與控制

王江華， 張 莉， 曾建學

(華北科技學院 電子信息工程學院，河北 三河 065201)

0 引 言

輪式機器人按照平衡性能分類，可分為靜態平衡機器人與動態平衡機器人兩種[1]。靜態平衡機器人一般具有3個以上的自由度，以保證機器人的靜態穩定性，但由于自由度的增加，勢必會造成驅動冗余，使得運動效率降低，同時由于機器人自由度的增加，使其對崎嶇路面的適應性變差；相比之下，動態平衡機器人由于其自由度少于平面運動的自由度，導致其不穩定性增加，但隨之而來的是靈活的運動特性和較高的運動效率。由于動態平衡機器人機構的獨特性，必須采用獨特的動態平衡原理才能實現正常運動。

本文所研究的球形全向移動自平衡機器人作為輪式機器人中的一種，由于其采用具有完整約束的全向輪，使其可以實現橫向移動而不打滑，輕易在平面內實現3個自由度運動，具有全向移動的特點[2]。機器人采用一個球形輪作為驅動輪，外觀上只具有一個自由度，因而其運動效率極高，理論上在任何路況中都能夠保證與路面等接觸。

該機器人理論原型為倒立擺，故也稱為“倒立擺機器人”，區別于傳統線性倒立擺，球形全向移動自平衡機器人將線性約束擴展為空間約束，這就對控制系統的穩定性與靈活性提出了更高的要求[3]。與傳統機器人相比，球形全向移動自平衡機器人具有以下特點：① 依靠單個球形輪作為支撐輪，能輕易實現360°全向運動；② 可以實現0半徑轉彎；③ 依據輪式機器人對地面的連續接觸性，故適用于全地形路面。

從理論研究角度，該機器人系統具有多變量、多驅動量、多自由度的特點，是一個極為復雜的MIMO非線性系統，再加上欠驅動的系統特性，可以為如今先進控制理論的驗證和優化提供理想實驗平臺。對球形全向移動自平衡機器人的研究不僅對于提高機器人對復雜地形環境的適應能力具有現實意義，還推動了先進控制理論的研究應用。

本文從球形全向移動自平衡機器人運動原理著手，對機器人的逆Atlas球面運動平臺(Inverse Atlas Spherical Motion Platform, IASMP)模型[5-6]進行分析，推導機器人運動控制方案；介紹機器人控制系統的設計和仿真模型的搭建,依據控制系統仿真模型，在Ballbot機器人上設計控制程序，以進行實物驗證，檢驗機器人控制系統對實現機器人的直立控制與運動控制的合理性與有效性。

1 基于IASMP模型的運動學和動力學模型分析

由圖1可知，Ballbot系列機器人使用3個直流無刷減速電機驅動3個全向輪，以控制機器人的球形輪，進而驅動機器人運動[4]，這是一個典型的IASMP模型。研究將從IASMP模型出發，對機器人進行運動學和動力學模型分析。

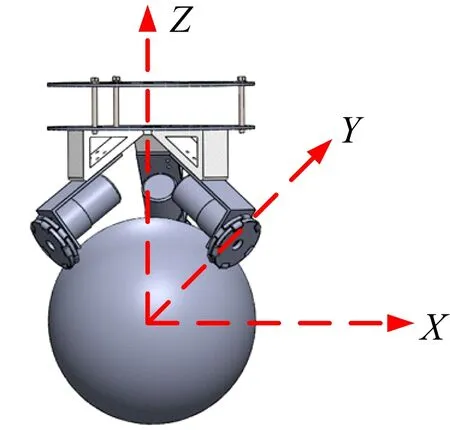
圖1 機器人仿真設計圖

機器人在不自旋的情況下，其運動可通過XOZ與YOZ兩個正交平面實現。定義圖1中YOZ平面中Y軸正向為機器人左向，定義XOZ平面中X軸正向為機器人前進方向。圖2表示機器人全向輪與球形輪的位置關系，圖中各參數的含義如表1所示。

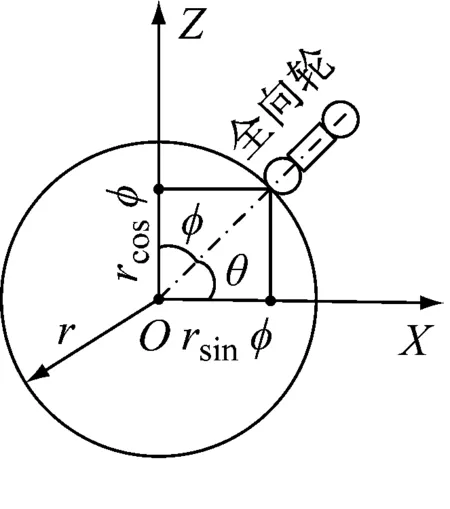
(a)

(b)

圖2 機器人坐標系定義

表1 參數定義

機器人3個全向輪在機器人本體坐標系中的位置向量為P，方向為由坐標原點指向全向輪與球面接觸點的方向[7]。實驗機器人其全向輪與球面接觸點和球心的連線與Z軸組成的傾角φ=45°

(1)

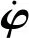
(2)

機器人采用雙鋁全向輪能夠實現360°運動，具有旋轉和側身機動性。對全向輪速度進行分解，分為沿驅動方向的速度vs和垂直于驅動方向的速度vf。其中vf是球形輪轉動所產生的速度，真正能夠改變球形輪運動狀態的是驅動方向的速度vs。故引出驅動向量si，按照圖2所示的全向輪在機器人坐標系的位置，可得到3個全向輪的驅動方向：

(3)

至此可推導出全向輪沿驅動方向的速度vsv：

(4)

由式(4)即可得到各全向輪驅動方向的實時轉速，對照圖2，可得出機器人向X、Y方向的實時速度。

當輪子繞著Y軸旋轉時，表示機器人正在沿前后方向運動，由圖2可得其驅動方向的速度為：

(5)

當輪子繞著X軸旋轉時，表示機器人正在沿左右方向運動，由圖2可得其驅動方向的速度為：

(6)

若考慮機器人的自旋，則其繞Z軸驅動方向的速度為：

(7)

由式(5)～(7)得出機器人X、Y、Z3個方向的速度合成之后所得到的3個全向輪的最終速度vi為：

(8)

由于機器人滾球輪X、Y方向的球面線速度即是機器人當前的速度，故記：

(9)

則式(8)可改寫成：

(10)

若設全向輪旋轉角速度為ωi，由式(2)可推導出球形輪的角速度矢量Ω與全向輪旋轉角速度的關系[8]：

(11)

式中,J表示機器人結構的雅可比矩陣，它將每個全向輪轉動的角速度映射到球體的角速度。解算之后的逆雅可比矩陣和雅可比矩陣定義如下：

(12)

式中，rb和rw分別表示滾球輪與全向輪的驅動半徑。由于仰角θ與天頂角φ之和是90°，即φ+θ=90°，由圖2可見，同時由此即可得到：sinθ=cosφ，cosθ=sinφ。故解算之后的逆雅可比矩陣和雅可比矩陣又可以改寫為：

(13)

故球體的角速度矢量Ω可由下式表出：

(14)

-rbΩ2i+rbΩ1j+0k=Vxi+Vyj+Vzk

(15)

故，對于機器人的速度V可表示如下：V=Vxi+Vyj+Vzk；其中3個分量：Vx,Vy,Vz在笛卡爾坐標系下可表示如下：

(16)

由式(16)可得三個速度分量的關系：

(17)

利用式(17)對時間的導數，可得到基于IASMP模型的運動學和動力學方程：

(18)

2 球形全向移動自平衡控制系統的設計

考慮到球形全向移動自平衡機器人與四軸飛控系統具有相似的特點，即非線性、強耦合、多變量等等[9]。因此，基于第1節對球形全向移動自平衡機器人的運動學分析，將四軸飛控的控制思路應用于機器人。

機器人控制部分，參考國外Pixhawk開源飛控，其旋翼控制部分主要采用串級PID控制技術，實現諸如誤差校正、姿態解算、姿態控制、位置控制等等，并取得了較好的控制效果。

四旋翼通過4個電動機實現空間6自由度的運動，只需克服空氣阻力(可以忽略不計)即可迅速改變機身姿態；而球形全向移動自平衡機器人則是通過3個直流無刷減速電動機，配合全向輪，通過無滑動的摩擦作用驅動球形輪，以實現機器人在平面上3自由度的運動。相比之下，四旋翼對于控制器的實時性、精確性要求更加嚴格；而對于該機器人，由于其控制輸出需要通過靜摩擦進行傳遞，期間必然存在一定的滯后性，對系統的實時性要求相對較低。基于以上對比分析，考慮通過串級PID技術，設計球形全向移動自平衡控制系統。

2.1 控制系統整體設計思路

基于對上一章機器人運動原理的分析，機器人控制可通過XOZ與YOZ兩個正交平面實現。依據MPU6050運動傳感器的軸向，以其水平X、Y軸對兩個平面建立兩套串級PID控制器，控制機器人的X、Y方向。根據運動傳感器MPU6050的6軸數據，使用4元素法，通過卡爾曼濾波與互補融合，解算出3軸歐拉角輸入X、Y方向的PID控制器的輸出，依據式(10)，將兩個方向的PID控制器輸出，映射到機器人3個電機上，以驅動球形輪實現機器人直立控制與全向移動。

2.2 機器人姿態控制方案

串級PID控制技術作為對傳統適用于線性時不變系統的單級PID控制技術的改進，通過內外兩環并聯調節，大大提高了系統的抗干擾能力[10]。參考飛控控制思路，確定以球形全向移動自平衡機器人的角度環作為主控制回路，主回路設計角度PID調節器作為主調節器；角速度環作為副回路，設計角速度PID調節器作為副調節器。主回路使用由MPU6050運動傳感器的6軸數據解算得到的3軸姿態角作為反饋信號，與設定值做差后作為主回路PID的輸入。主回路的角度PID輸出與角速度融合后直接作為副回路的輸入，副回路PID調節器輸出作用到執行機構[11]。

球形全向移動機器人串級PID控制系統框圖如3所示。由圖3可知，角度/角速度串級控制系統執行順序是先執行角度控制，再執行角速度控制。為避免內外環產生共振，也考慮到進一步提高反應速度和工作頻率，將系統角速度控制周期設為角度控制周期的一半，平均每5 ms角速度PID控制器進行一次控制更新，每10 ms角度PID控制器進行一次控制更新。如此設置，一來可以使得內環角速度對干擾能夠進行快速而有效抑制，二來也將外環的誤差對內環的影響降到最低，進一步增強了機器人系統的抗擾性。

2.3 機器人全向移動控制方案

對于運動控制，就四旋翼控制系統而言主要包括4個量：油門與3軸姿態角。由于空中運動的空間優勢，使得其具有較大的可控制裕量，通過設定其姿態角，產生姿態偏差，在姿態控制器的調節下趨使其向某個特定方向運動[12]。而對于Ballbot機器人，其偏角的角度需要考慮驅動輪的驅動力，驅動力受重力分力的限制，若不外加支撐，其可調裕度非常有限，稍微控制不好就會導致控制失效。另外由于機器人的速度是根據3個電動機編碼器解算得出的，該機器人又屬于動穩定機器人，故其解算數值必然存在較大噪聲[13]。但由于機器人對于控制的實時性要求較低，故本文通過中值濾波與均值濾波相互配合實現對機器人運動速度的測算。

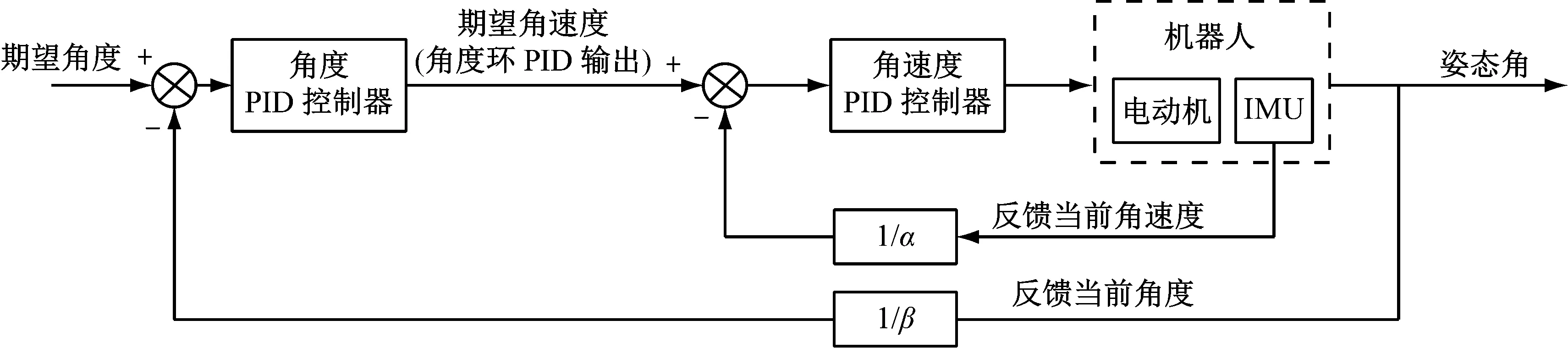
圖3 角度/角速度串級PID原理框圖

基于此本文提出對已有的角度/角速度串級PID進行改進，在角度環外再加入速度環，將速度環的輸出進行量程轉換與當前反饋的姿態角進行疊加，共同作為角度環的輸入，構成3閉環控制系統。即將速度控制轉換成角度控制，通過直立環調節速度響應，使得控制作用更加平滑[14]。

機器人的運動控制框圖如圖4所示。

圖4 機器人運動控制框圖

3 機器人控制系統仿真模型的設計

機器人控制主要由X、Y方向的兩個串級PID控制器組成，由于機器人結構的對稱性，兩個控制器設計方法基本一致，僅3個電動機對應X、Y兩個方向的轉向以及組合輸出的比例有所不同。故僅從X方向控制器仿真模型的設計出發展開介紹。

機器人控制系統仿真模型的設計主要包括兩部分：基于Matlab的SimMechanics工具箱設計機器人動力學仿真模型；機器人串級PID控制器Simulink仿真模型。

3.1 機器人動力學仿真模型

Matlab SimMechanics工具箱[15-16]主要用于多體動力機械系統及其控制的建模仿真。使用工具箱按照系統的運動機理，設計出對應的剛體、鉸鏈、約束以及外力，以此搭建系統的剛體仿真模型，在仿真時，使用SimMechanics可視化工具，可將機構系統及其運動轉化為直觀的動畫顯示。區別于其他機械系統仿真軟件，SimMechanics可以與Simulink結合，為控制系統的仿真設計提供了方便。

本文為簡化模型，將3個全向輪直接轉換為X、Y兩個方向的作用力，對球形全向移動機器人建立SimMechanics模型如圖5所示。

3.2 機器人控制系統仿真模型

機器人控制系統使用串級PID控制器進行設計，控制器由速度、角度、角速度組成3閉環控系統，控制器輸出直接作用到機器人的動力學模型，得到各狀態變量的反饋值，并送往控制器反饋端進行調節。機器人控制系統的Simulink仿真模型如圖6所示。

3.3 機器人運動控制仿真

為驗證機器人運動控制的有效性，設計驗證試驗，設置機器人初始參數：[0,0,0,0,0]，即3個姿態角控制量均為0°，機器人兩個控制方向的速度給定值為0。隨后，給定X方向的速度設定值設定單個方波信號，觀察機器人姿態角的變化。

由仿真結果可知(見圖7),當給定信號發出后，機器人速度環輸出引起機器人姿態變化，在姿態環的控制下，驅使機器人朝著X方向運動。當控制信號撤除后機器人能夠及時矯正姿態，保持直立狀態。由仿真結果可以看出,控制器能夠完成設定任務。

4 實物驗證

為進一步驗證控制系統設計的合理性與有效性，本文根據控制器仿真模型，對Ballbot機器人設計實物驗證。設計的機器人如圖8所示。

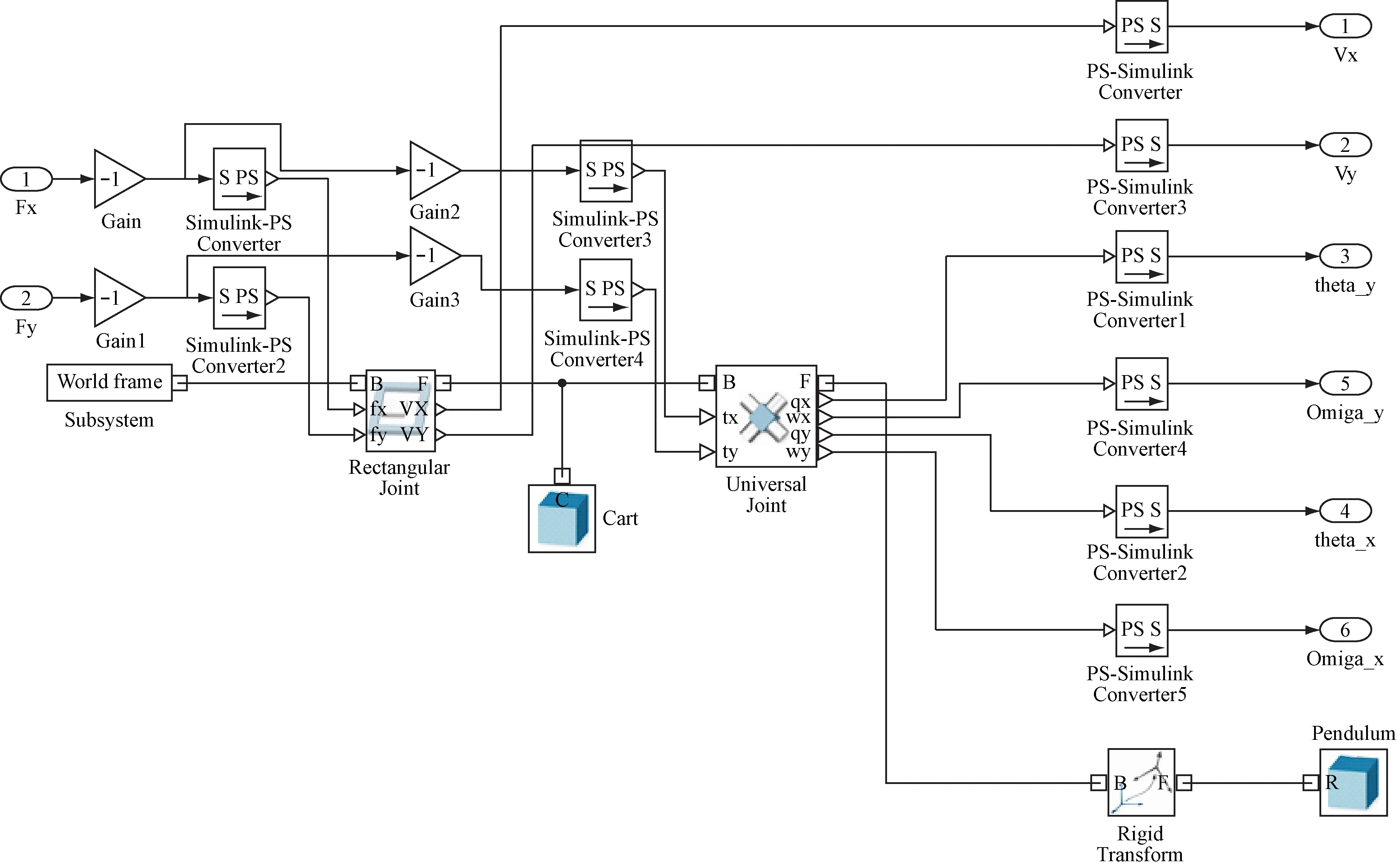
圖5 SimMechanics動力學模型圖

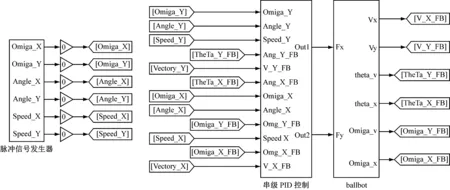
圖6 機器人控制系統仿真模型

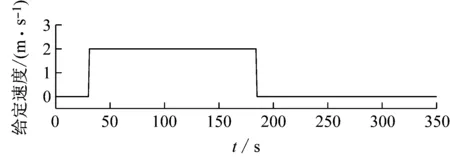
圖7 運動控制器產生的姿態變化曲線

圖8 Ballbot機器人實物圖

本文所設計的實驗分為兩個部分，實驗檢驗機器人姿態控制和機器人運動控制能力。

實驗主要通過機器人機身運動傳感器的3個姿態角(俯仰角Ax、翻滾角Ay、偏航角Az)反映機器人在靜止狀態下的平衡情況以及運動過程中的方向偏差情況；通過機器人的X、Y兩個方向的速度(Vx、Vy)反映機器人定點直立、速度配合效果。機器人實物測試數據如圖9所示。

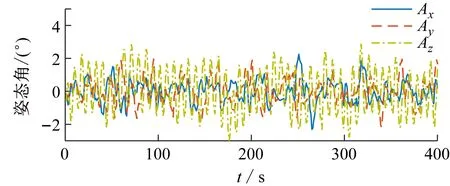
圖9 姿態控制測試結果圖

在姿態控制器的控制下，機器人上電初始化后，直接進入定點直立模式，不需要對機器人進行任何額外設定。通過機器人3個姿態角的變化曲線以及機器人速度變化曲線可看出：機器人一直在原地調整姿態，各姿態角度控制在3°以內，機器人的運動速度一直在原點附近波動，同時機器人X-Y方向上的速度也在x=0附近調整，保證機器人可以在原點保持直立。據此可判定機器人能夠完成直立狀態下的姿態控制。

機器人運動控制，主要通過測試機器人進行直線運動與圓周運動來檢驗機器人運動方向的準確性與速度控制的穩定性。機器人運動速度通過圖10可以看出在進行直線運動與圓周運動時，機器人均能夠平穩的調節運動速度以達到控制目的。

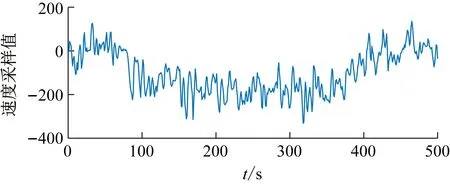
圖10 運動控制速度曲線圖

由圖11所示，在機器人直線運動測試中，機器人Yaw軸的航向角變化曲線可知，機器人在運動過程中，其航向角變化在3°以內，可認為機器人運動方向穩定，體現出速度控制的有效性。

圖11 機器人運動方向曲線圖

5 結 語

本文重點研究球形全向移動自平衡機器人控制系統的設計。控制系統的控制對象是一種以運動高效性、靈活性為特點，并以單個球形輪作為運動輪的全向移動機器人(Ballbot機器人)。實現關鍵在于設計以串級PID技術作為控制方式的控制器，以實現機器人的直立和全向移動。

本文從機器人的IASMP模型出發，對機器人進行運動學和動力學分析，由此得出機器人3個無刷減速直流電動機的組合控制方案；并在SimMechanics工具箱設計機器人動力學仿真模型的基礎上，設計機器人控制系統的Simulink模型進行仿真；同時按照仿真模型的設計方法，在實驗室Ballbot機器人上設計軟件控制器，實現了機器人定點直立與全向移動控制。

球形全向移動自平衡機器人控制系統具有多自由度、多驅動量、多傳感器的特點，是一個極為復雜的MIMO非線性系統，再加上欠驅動的系統特性，可以為如今的先進控制理論的驗證和優化提供理想實驗平臺。對球形全向移動自平衡機器人的研究不僅對于提高機器人對復雜地形環境的適應能力具有現實意義，也推動了先進控制理論的研究應用。