30日齡翹嘴鱖形態性狀與體質量之間的關系

劉國興 ，孫海峰 ，鄭友 ，郝忱 ，丁淑燕 ，鄭嘯宇 ，史楊白

（1.江蘇省淡水水產研究所，江蘇 南京 210017；2.江蘇省農業種質資源保護與利用平臺,江蘇 南京 210014）

翹嘴鱖（Siniperca chuatsi）別稱桂魚、鱖花魚和季花魚等，隸屬鱸形目（Perciformes），暖鱸科（Percichthyidae），鱖屬（Siniperca），是我國重要的淡水養殖名優品種。目前，我國翹嘴鱖產業發展前景廣闊，但在育種方面仍面臨著諸多問題，長期近親繁殖導致養殖翹嘴鱖出現明顯的種質退化，集中表現為生長速度降低、抗病和抗逆性能下降，已經嚴重制約了翹嘴鱖養殖業的持續健康發展[1-2]。因此，開展翹嘴鱖選育種工作，培育出生長快、抗逆性強的優良新品種顯得尤為迫切。

體質量是水產動物選育過程中的主要目標性狀，也是生產性能的直接反映[3]。而在實際工作中，體質量性狀不夠直觀，相比之下形態性狀具有可度量性和直觀性，是遺傳育種中進行選擇和定向培育的常用指標[4]。利用多元分析弄清形態性狀與體質量之間的關系以及對體質量的直接影響大小，通過形態性狀輔助體質量達到選種目的，可以顯著提高選擇準確性和選育效果[5-6]。近年來，國內外學者圍繞主要水產品種開展了形態性狀與體質量之間關系的研究。Reis Neto等[7]采用通徑分析評估了魚體形態性狀與體質量間的相互關系。胡彥波等[4]通過模型擬合篩選，獲得了能夠反映花鱸（Lateolabrax maculatus）各形態性狀與體質量關系的最佳模型。孫海峰等[8]應用相關分析、通徑分析和多元回歸分析，定量分析了羅氏沼蝦（Macrobrachium rosenbergii）形態性狀與體質量的相關性。該研究采用相關分析、通徑分析和多元回歸分析，確定了影響30日齡翹嘴鱖體質量的主要形態性狀及其對體質量影響的直接和間接作用的大小，建立了形態性狀與體質量間的多元線性最優回歸方程，以期為翹嘴鱖人工選育工作提供參考資料。

1 材料與方法

1.1 試驗動物

試驗動物取自江蘇省淡水水產研究所揚中基地，為同一批次繁殖、同池培育的30日齡翹嘴鱖幼魚。隨機選取200尾幼魚進行試驗測量，待測幼魚健康無病、魚體完整無損傷，分別測量其體質量（y）、全長（x1）、體長（x2）、吻長（x3）、眼徑（x4）、體厚（x5）、體高（x6）、頭長（x7）、尾柄長（x8）和尾柄高（x9）共 10個指標。

1.2 測量方法

測量前使用丁香酚（30 mg/L）對魚體進行麻醉，采用吸水紙吸干魚體表面水分，然后用電子天平稱量體質量，精確到0.01 g；參照竇亞琪等的方法[9]，用電子數顯卡尺測量各項表型形態性狀，精確到0.01 mm。

1.3 數據處理

運用Excel 2019和SPSS 22.0軟件對各性狀測量數據進行綜合整理和統計分析，通過計算均值、標準差和變異系數，獲得各性狀的表型統計量，然后進行表型相關分析。根據相關矩陣建立正則方程組，求得各形態性狀對體質量的通徑系數，并剖析各形態性狀對體質量的直接作用和間接作用，計算決策系數[5]。利用逐步回歸分析方法，建立形態性狀對體質量的多元線性最優回歸方程。

2 結果與分析

2.1 所測性狀的表型統計量

所測性狀的數據資料經整理分析后的表型統計量見表1。從表1可以看出，30日齡翹嘴鱖體質量的變異系數最大，達26.73%；各形態性狀的變異系數相對較小，其大小順序依次為：體厚＞尾柄長＞吻長＞尾柄高＞體高＞頭長＞全長＞體長＞眼徑，眼徑在所測形態性狀中變異系數最小，僅為8.79%。

2.2 性狀間的相關系數

所測各性狀兩兩之間的相關系數（Pearson相關系數）見表2。從表2可以看出，30日齡翹嘴鱖各形態性狀與體質量之間的相關系數均極具統計學意義水平（P＜0.01），其大小順序依次為：體高＞體長＞全長＞頭長＞吻長＞尾柄高＞體厚＞眼徑＞尾柄長。體高與體質量的相關系數最大（達0.927），尾柄長與體質量的相關系數最小（0.622）。

表2 性狀間的相關系數

2.3 各性狀的正態分布檢驗

在采取通徑分析、多元回歸分析之前，應對各性狀數據進行正態分布檢驗，只有當各性狀數據為正態變量或近似正態變量時，之后的分析才具有統計學意義[10]。由于該研究n=200屬于大樣本，所以采用Kolmogorov-Smirnov法進行正態分布檢驗。所測30日齡翹嘴鱖各性狀的正態分布檢驗結果見表3。從表3可以看出，顯著性均大于0.05，表明各性狀數據均服從正態分布、均為正態變量，可以進行回歸分析。

表3 各性狀的正態分布檢驗結果

2.4 多元回歸方程的建立

以體質量為因變量，以全長、體長、吻長、眼徑、體厚、體高、頭長、尾柄長和尾柄高為自變量進行逐步回歸。模型概述輸出結果見表4。從表4可以看出，隨著自變量被逐步引入回歸方程，回歸方程的復相關系數R和決定系數R2均逐漸增大，說明引入的自變量對因變量的作用在增加。與模型1、2和3相比，模型4的R2最大（達0.935），則剩余因子e=最小（0.255），說明模型4對因變量有影響的自變量考慮最全面，與數據的擬合程度最好。體質量方差分析見表5。從表5可以看出，顯著性均小于0.05，說明所測翹嘴鱖的體質量在個體間存在差異性。

偏回歸系數和回歸系數的顯著性檢驗見表6。從表6可以看出，體高、體長、尾柄長和體厚顯著性檢驗結果均小于0.05，表明自變量與因變量之間差異具有統計學意義，都應留在方程中。30日齡翹嘴鱖的體質量（y）與形態性狀（x）的多元線性最優回歸方程為：y=-0.672+0.053x6+0.019x2+0.015x8+0.019x5，式中 y、x6、x2、x8和x5分別為體質量、體高、體長、尾柄長和體厚。

表4 模型概述輸出結果

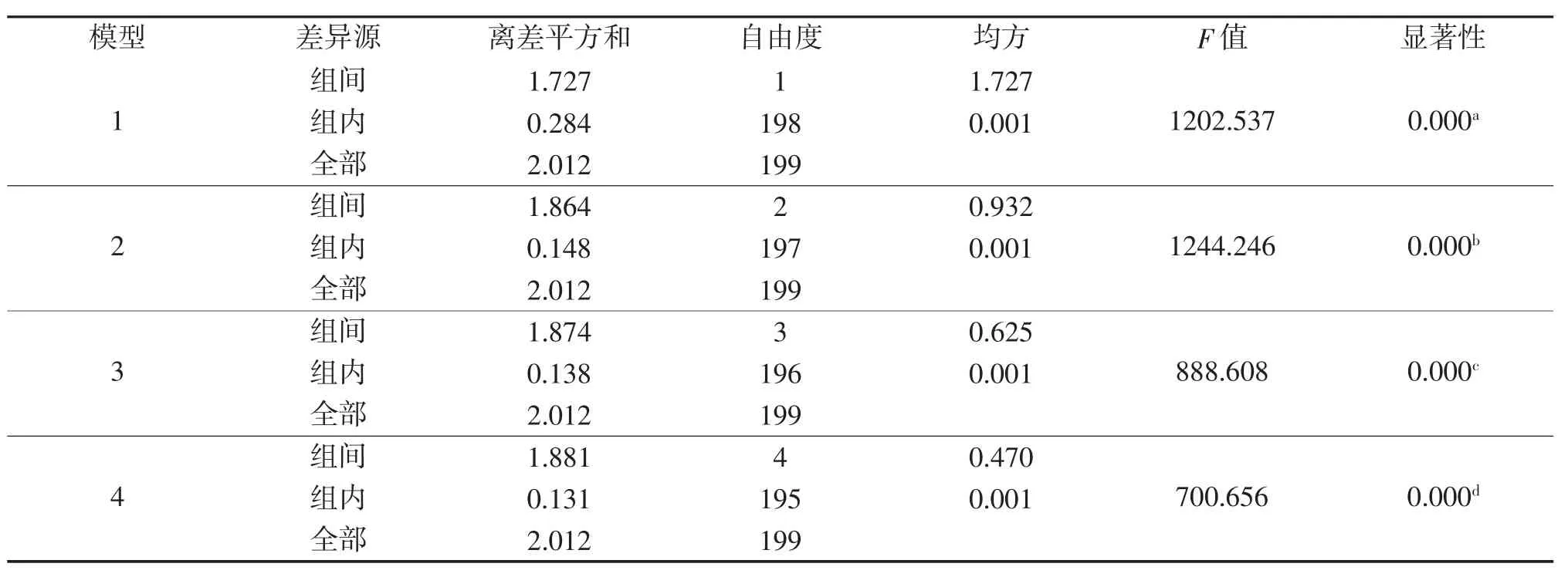
表5 體質量方差分析

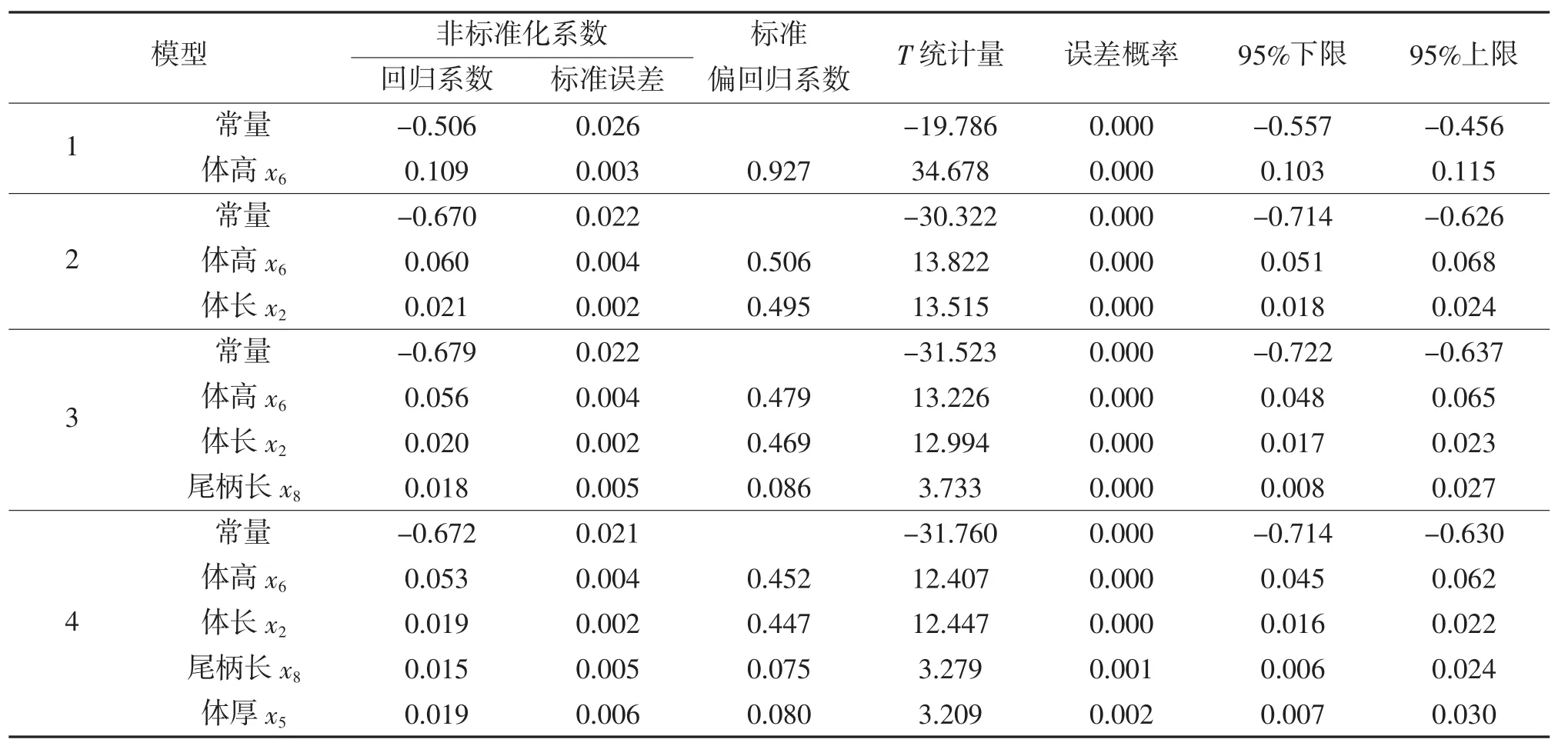
表6 偏回歸系數和回歸系數的顯著性檢驗

2.5 間接通徑系數與決策系數的計算

從表 2 可以看出，體高（x6）、體長（x2）、尾柄長（x8）與體厚（x5）兩兩之間的相關系數分別為r62=r26=0.850、r68=r86=0.566、r65=r56=0.653、r28=r82=0.563、r25=r52=0.642、r85=r58=0.488；x6、x2、x8、x5與體質量（y）的相關 系數分別為 r6y=0.927、r2y=0.925、r8y=0.622、r5y=0.699。從表 6 可以看出，x6、x2、x8、x5對 y 的通徑系數（直接作用）分別為P6y=0.452、P2y=0.447、P8y=0.075、P5y=0.080。根據通徑分析的理論可知，r6y=P6y+r26×P2y+r86×P8y+r56×P5y=0.927，r2y=P2y+r62×P6y+r82×P8y+r52×P5y=0.925，r8y=P8y+r68×P6y+r28×P2y+r58×P5y=0.622，r5y=P5y+r65×P6y+r25×P2y+r85×P8y=0.699（計算結果與表 2 一致）。

x6通過x2對y的間接通徑系數為：r26×P2y=0.380，x6通過x8對y的間接通徑系數為：r86×P8y=0.042，x6通過x5對y的間接通徑系數為：r56×P5y=0.052。x2通過x6對y的間接通徑系數為：r62×P6y=0.384，x2通過x8對y的間接通徑系數為：r82×P8y=0.042，x2通過x5對y的間接通徑系數為：r52×P5y=0.051。x8通過x6對y的間接通徑系數為：r68×P6y=0.256，x8通過x2對y的間接通徑系數為：r28×P2y=0.252，x8通過x5對y的間接通徑系數為：r58×P5y=0.039。x5通過x6對y的間接通徑系數為：r65×P6y=0.295，x5通過x2對y的間接通徑系數為：r25×P2y=0.287，x5通過x8對y的間接通徑系數為：r85×P8y=0.037。

決策系數是通徑分析中的決策指標，可將各自變量對因變量的綜合作用進行排序，從而確定主要決策變量和限制變量[12]。決策系數的計算公式：R2（i）=2Piy×riy-，式中Piy為xi對y的通徑系數（直接作用），riy為xi與y的相關系數。R2（i）＞0，表明xi對y起增進作用；R2（i）＜0，表明xi對y起抑制作用[11-12]。

30日齡翹嘴鱖4個形態性狀對體質量的影響見表7。從表7可以看出，4個形態性狀對體質量的決策系數大小順序依次為：R2（6）＞R2（2）＞R2（5）＞R2（8）＞0。因此，體高x6為主要決策變量（直接決定作用最大），體高x6、體長x2、尾柄長x8和體厚x5對體質量y均起增進作用。

表7 30日齡翹嘴鱖4個形態性狀對體質量的影響

3 討論

3.1 相關分析和通徑分析的特點及多元回歸方程的建立

在相關分析中，相關系數是兩個變量之間相互關系的綜合體現，包含了兩者間的直接關系和通過其他變量影響的間接關系[13]。因此，單純依據性狀間的相關系數不能準確評判兩性狀間的真實關系，而通徑分析能夠將性狀間的表型相關剖分為直接作用和間接作用，直接作用反映兩性狀間的本質關系[14]。該研究結果表明，30日齡翹嘴鱖的全長、體長、吻長、眼徑、體厚、體高、頭長、尾柄長和尾柄高與體質量之間的相關系數均達到極具統計學意義水平（P＜0.01），但這并不能表示性狀間的真實關系，只能作為進一步分析的基礎，確保通徑分析和多元回歸分析具有統計學意義[15]。

通徑系數表示自變量對因變量直接影響的大小，其隨著所選自變量的數量和性質的不同而變化，涉及的自變量越多，分析結果越可靠，但統計分析就越復雜[13]。通常情況下，選擇與因變量的相關系數達到顯著水平的自變量，將相關系數不顯著的自變量剔除[16]。為量化形態性狀與體質量之間的真實關系，該研究采用通徑分析和逐步回歸分析的方法，建立了以體質量為因變量，體高、體長、尾柄長和體厚為自變量的多元線性最優回歸方程。

3.2 影響翹嘴鱖體質量的主要性狀的確定

在相關分析的基礎上，進行通徑系數和決定系數分析時，只有當決定系數R2大于或等于0.85（即85%），才表明影響因變量的主要自變量已經找到[17]。本研究中，建立的形態性狀與體質量的回歸模型經統計學檢驗達顯著水平（P＜0.05），模型決定系數R2達0.935，說明模型入選的體高、體長、尾柄長和體厚是影響體質量的主要性狀，其他性狀對體質量的影響相對較小。這與體高較高、體厚較厚、體長和尾柄長較長的個體具有較大的幾何空間，有利于蛋白質、脂肪等營養物質的積累貯存，相應體質量亦較重的實際生產經驗一致[16]。何小燕等[18]研究發現，大口黑鱸（Micropterus salmoides）體質量選育過程中，體寬、體長和眼間距可作為重要的測度指標。杜華等[19]報道，全長、體長、體高和尾柄高是影響鴨綠沙塘鱧（Odontobutis yaluensis）體質量的重點性狀，在選育過程中應該重視這4個重點性狀。楊貴強等[3]研究表明，影響硬頭鱒（Oncorhynchus mykiss）幼魚體質量的主要表型性狀為體長、體高、體厚和眼徑。類似研究結果出現差異可能是所選形態性狀不同以及各種魚類形態性狀對體質量的影響效果異同造成的[18]。該研究采用相關分析、通徑分析和多元回歸分析，確定了影響30日齡翹嘴鱖體質量的主要形態性狀為體高、體長、尾柄長和體厚。這4個形態性狀中，體高對體質量的直接作用（0.452）和決策系數（0.634）均為最大，說明體高為主要決策變量。以上研究成果為翹嘴鱖選育工作提供了理論依據和技術參數，可用于指導翹嘴鱖良種選育工作。