MATLAB軟件在高等數學教學中的應用
黃婷婷 揭陽職業技術學院 廣東揭陽 522000
一、引言
高等數學作為高等院校理工科專業的必修基礎課程,主要包含極限與連續、導數與微分、不定積分和定積分、常微分方程、矩陣等內容。該門課程理論嚴密,知識點復雜且抽象,不少同學覺得課堂的內容難以理解和掌握。傳統的教學方式主要以課本的數學知識為基礎,內容較為枯燥,容易與實際應用脫節 而與生活實際、生產實際相結合的數學模型中,往往需要比較復雜的計算,而這些計算又會占用大量的時間,影響學科知識的全面掌握,不利于提升學生學習的主動性和創造性。因此,MATLAB軟件作為輔助的手段應用到高數課堂中,可為數學教學和實際應用架起橋梁。
MATLAB是由Mathworks公司發布的集算法開發、數據可視化、數據分析及數值計算于一體的高級技術計算語言和交互式環境,廣泛應用于信號和圖像處理、通信、控制系統設計、測試和測量等眾多領域。
本文主要介紹如何使用MATLAB軟件講解高等數學中函數間斷點的知識點,以幾個簡單的例題,探討將MATLAB軟件輔助高等數學課堂教學的優點,使一些抽象的公式或運算能用可視化的圖像表示出來,達到傳統教學無法實現的效果。以此調動學生學習高等數學的積極性,進一步改善高等數學的教學效果。
二、MATLAB在高等數學教學中的應用
(一)函數間斷點的概念
如果函數f(x)在點x0處不滿足連續的條件,則稱函數f(x)在點x0處不連續或間斷。點x0叫做函數f(x)的不連續點或間斷點。
如果函數f(x)在點x0處有下列三種情形之一,則點x0為f(x)的間斷點。
1.在點x0處f(x)沒有定義。
2.limx→x0f(x)不存在。
3.雖然f(x0)有定義,且limx→x0f(x)存在,但limx→x0f(x)≠ f(x_0) 。
(二)函數的間斷點求解
在MATLAB軟件中,可以通過命令limit實現函數的極限計算。同時,可以利用plot或fplot命令繪制二維曲線函數圖形,通過圖像更直觀地理解相關概念。
在MATLAB的命令窗口輸入:
x=-0.5:0.01:0.5;
legend('y=x*cos(1/x)')% 顯示圖例
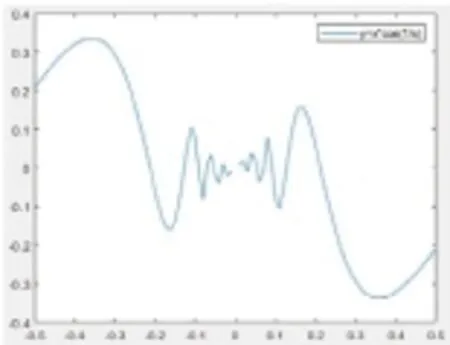
圖1 函數y=xcos 的圖像
syms x% 定義符號變量
limit(x.*cos(1./x),x,0)%求函數在自變量x趨于0時的極限
limit(x.*cos(1./x),x,0,'left')%求函數在自變量x趨于0時的左極限
limit(x.*cos(1./x),x,0,'right')%求函數在自變量x趨于0時的右極限
執行結果:
ans =0
ans =0
ans =0
三、小結
以上題目介紹了MATLAB軟件在求函數間斷點的應用。利用不復雜的命令可以實現高等數學中的很多基本計算,且準確率高,運行效率高。將MATLAB軟件應用于高等數學的輔助教學,不僅能提高計算的效率和準確度,還有利于培養學生借助計算機解決數學問題的思維方式,既能掌握必須的數學基礎知識,又能有效的建立起課堂與生產實際的聯系,為今后走上工作崗位打好基礎。

